Hungerford T.W., Shaw D.J. Contemporary Precalculus: A Graphing Approach

Подождите немного. Документ загружается.

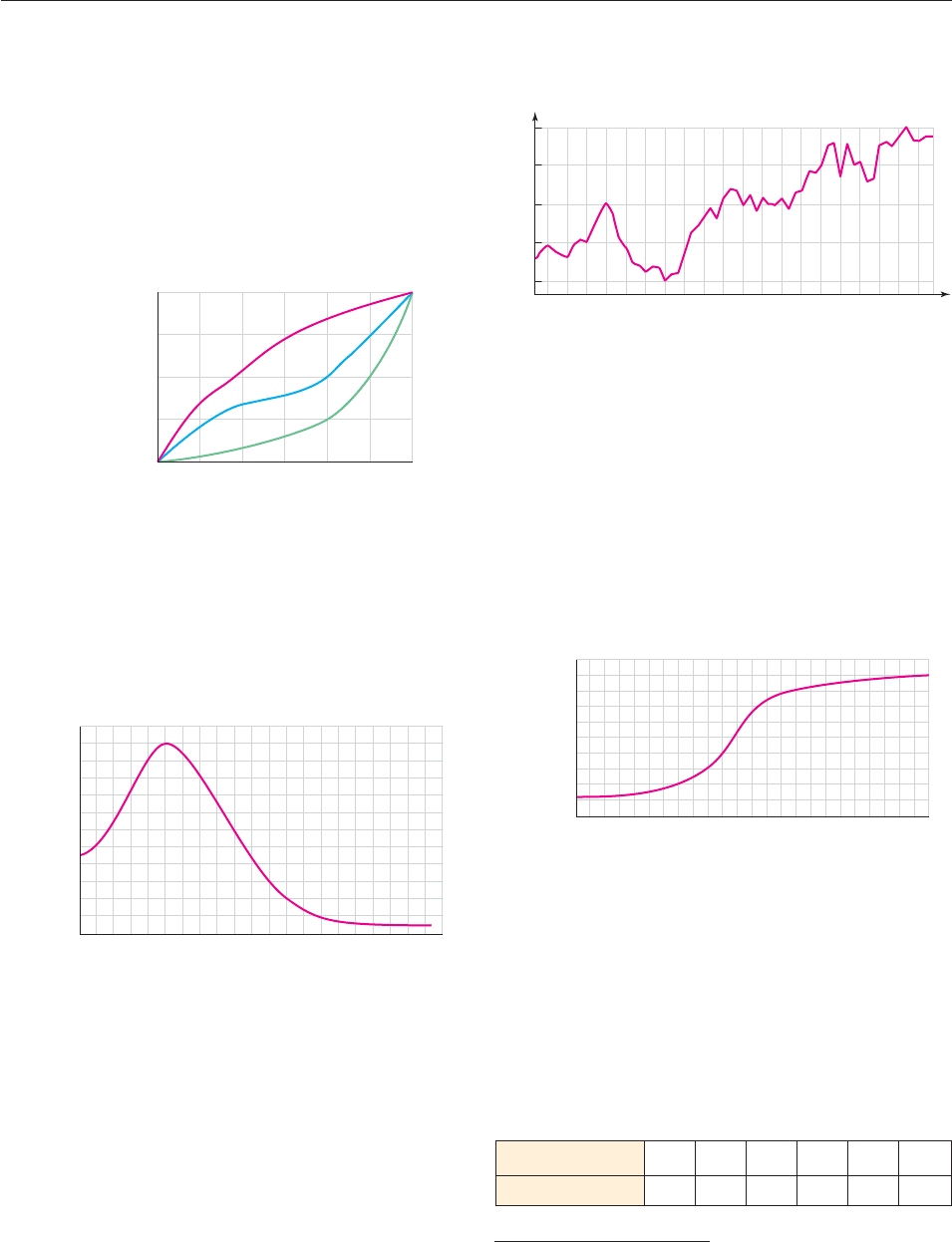
(a) What is the average speed of each car during this

16-second interval?

(b) Find an interval beginning at t  4 during which the

average speed of car D was approximately the same as

the average speed of car C from t  2 to t  10.

D traveled at a higher average speed than car C from

t  4 to t  10.”

31. The figure shows the profits earned by Soupy Soy Sauce

during the last quarters of three consecutive years.

(a) Explain why the average rate of change of profits from

October 1 to December 31 was the same in all three years.

(b) During what month in what year was the average rate of

change of profits the greatest?

32. The graph in the figure shows the chipmunk population in a

certain wilderness area. The population increases as the

chipmunks reproduce but then decreases sharply as preda-

tors move into the area.

(a) During what approximate time period, beginning on

day 0, is the average growth rate of the chipmunk pop-

ulation positive?

(b) During what approximate time period, beginning on

day 0, is the average growth rate of the chipmunk pop-

ulation 0?

lation from day 50 to day 100? What does this number

mean?

(d) What is the average growth rate from day 45 to day 50?

From day 50 to day 55? What is the approximate aver-

age growth rate from day 49 to day 51?

2000

1000

50 100

Days

150 200

Population

400,000

300,000

200,000

100,000

Oct. 1 Nov. 1

2006

2007

2008

Dec. 1

Profit

216 CHAPTER 3 Functions and Graphs

33. The following is a graph of the price of a share of stock in the

International House of Pancakes from June of 2001 through

June of 2006

(a) What was the average rate of change of IHOP stock (in

dollars per year) between September of 2001 and

March of 2002?

(b) What was the average rate of change of IHOP stock

between March of 2002 and January of 2003?

between June of 2001 and June of 2006?

34. Lucy has a viral flu. How bad she feels depends primarily

on how fast her temperature is rising at that time. The figure

shows her temperature during the first day of the flu.

(a) At what average rate does her temperature rise during

the entire day?

(b) During what two-hour period during the day does she

feel worst?

the afternoon, during which she feels about the same

(that is, during which her temperature is rising at the

same average rate).

35. The table shows the average weekly earnings (including over-

time) of production workers and nonsupervisory employees

in industry (excluding agriculture) in selected years.*

98°

99°

100°

101°

102°

103°

2 4 6 8 10 12 14 16 18 20 22 24

Time of Day

Temperature

02 03 04 05 06

Price ($)

*U.S. Bureau of Labor Statistics.

Year 1980 1985 1990 1995 2000 2005

Weekly Earnings $191 $257 $319 $369 $454 $538

(a) Use linear regression to find a function that models this

data, with x  0 corresponding to 1980.

(b) According to your function, what is the average rate of

change in earnings over any time period between 1980

and 2005?

in earnings from 1980 to 1990 and from 2000–2005.

How do these rates compare with the ones given by the

model?

(d) If the model remains accurate, when will average

weekly earnings reach $600?

36. The estimated number of 15- to 24-year-old people world-

wide (in millions) who are living with HIV/AIDS in

selected years is given in the table.*

SECTION 3.7 Inverse Functions 217

(a) Use linear regression to find a function that models this

data, with x  0 corresponding to 2000.

(b) According to your function, what is the average rate of

change in this HIV/AIDS population over any time

period between 2001 and 2009?

change in this HIV/AIDS population from 2001 to 2009.

How does this rate compare with the one given by the

model?

(d) If the model remains accurate, when will the number

of people in this age group with HIV/AIDS reach

25 million?

*Kaiser Family Foundation, UNICEF, U.S. Census Bureau.

Year 2001 2003 2005 2007 2009

15- to 24-year-olds 12 14.5 17 19 20.5

with HIV/AIDS

3.7 Inverse Functions*

■ Determine graphically if a function is one-to-one.

■ Find inverse functions algebraically.

■ Explore the properties of inverse functions.

■ Graph inverse functions.

Consider the functions f and h given by these tables:

With the function h, two different inputs (2 and 4) produce the same output 3.

With the function f, however, different inputs always produce different outputs.

Functions with this property have a special name. A function f is said to be one-

to-one if distinct inputs always produce distinct outputs, that is,

if a  b, then f (a)  f (b)

In graphical terms, this means that two points on the graph, (a, f (a)) and

(b, f (b)), that have different x-coordinates [a  b] must also have different y-

coordinates [ f (a)  f (b)]. Consequently, these points cannot lie on the same

horizontal line because all points on a horizontal line have the same y-

coordinate. Therefore, we have this geometric test to determine whether a

function is one-to-one.

Section Objectives

f-input 2 10 1 2

f-output 3 21 4 5

h-input 12345

h-output 13 0 3 2

*This section is used only in Section 5.3, Special Topics 5.3.A, and Section 7.4. It may be postponed

until then.

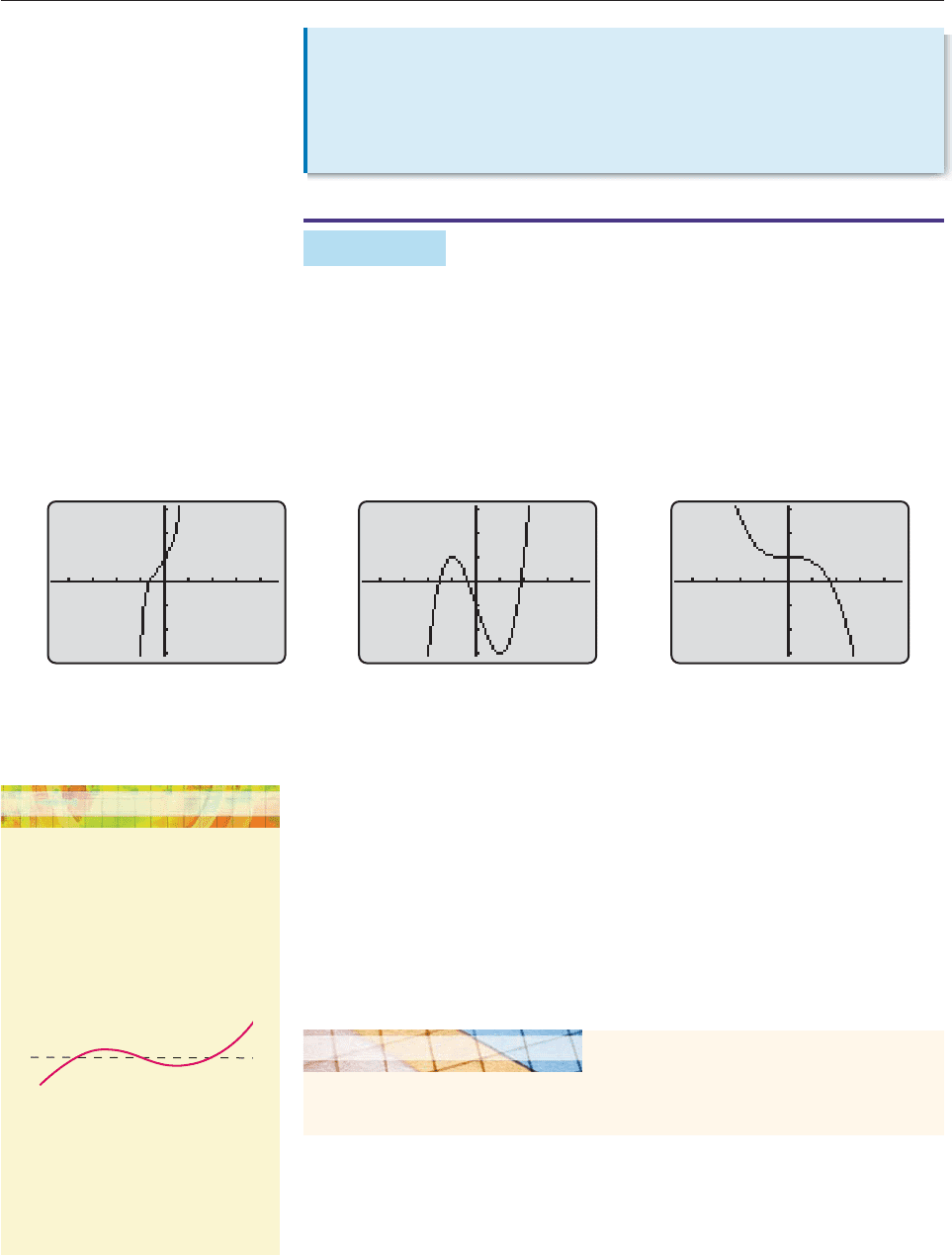
EXAMPLE 1

Which of the following functions are one-to-one?

(a) f(x)  7x

 3x

 2x

 2x  1

(b) g(x)  x

 3x  1

SOLUTION Complete graphs of each function are shown in Figure 3–54.

Figure 3–54

(a) The graph of f in Figure 3–54(a) passes the horizontal line test, since no hor-

izontal line intersects the graph more than once. Hence, f is one-to-one.

(b) The graph of g in Figure 3–54(b) obviously fails the horizontal line test

because many horizontal lines (including the x-axis) intersect the graph more

than once. Therefore, g is not one-to-one.

ment. So h appears to fail the Horizontal Line Test because the horizontal line

through (0, 1) seems to intersect the graph infinitely many times. But appear-

ances are deceiving.

3.1

4.7

⫺4.7

⫺3.1

3.1

4.7

⫺4.7

⫺3.1

3.1

4.7

⫺4.7

⫺3.1

(a) (b) (c)

218 CHAPTER 3 Functions and Graphs

The Horizontal

Line Test

If a function f is one-to-one, then it has this property:

No horizontal line intersects the graph of f more than once.

Conversely, if the graph of a function has this property, then the function is

one-to-one.

Graph h(x)  1  .2x

and use the trace feature to move from left to right along the

“horizontal” segment. Do the y-coordinates stay the same, or do they decrease?

GRAPHING EXPLORATION

The Exploration shows that the graph is actually falling from left to right, so that

each horizontal line intersects it only once. (It appears to have a horizontal seg-

ment because the amount the graph falls there is less than the height of a pixel on

the screen.) Therefore, h is a one-to-one function. ■

TECHNOLOGY TIP

Although a horizontal segment may

appear on a calculator screen when

the graph is actually rising or falling,

there is another possibility. The graph

may have a tiny wiggle (less than the

height of a pixel) and thus fail the hor-

izontal line test:

You can usually detect such a wiggle

by zooming in to magnify that portion

of the graph or by using the trace fea-

ture to see whether the y-coordinates

increase and then decrease (or vice

versa) along the “horizontal” segment.

The function f in Example 1 is an increasing function (its graph is always

rising from left to right), and the function h is a decreasing function (its graph is

always falling from left to right). Every increasing or decreasing function is nec-

essarily one-to-one because its graph can never touch the same horizontal line

twice (it would have to change from rising to falling, or vice versa, to do so).

INVERSE FUNCTIONS

We begin with a simple example that illustrates the basic idea of an inverse

function. Consider the one-to-one function f introduced at the beginning of this

section.

Now define a new function g by the following table (which simply switches the

rows in the f table).

Note that the inputs of f are the outputs of g and the outputs of f are the inputs of

g. In other words,

Domain of f  Range of g and Range of f  Domain of g.

The rule of g reverses the action of f by taking each output of f back to the input it

came from. For instance,

g(4)  1 and f (1)  4

g(3) 2 and f (2) 3

and in general,

g(y)  x exactly when f (x)  y.

We say that g is the inverse function of f.

The preceding construction works for any one-to-one function f. Each output

of f comes from exactly one input (because different inputs produce different out-

puts). Consequently, we can define a new function g that reverses the action of

f by sending each output back to the unique input it came from. For instance, if

f (7)  11, then g(11)  7. Thus, the outputs of f become the inputs of g, and we

have this definition.

SECTION 3.7 Inverse Functions 219

f-input 2 10 1 2

f-output 3 21 4 5

g-input 3 21 4 5

g-output 2 10 1 2

Inverse

Functions

Let f be a one-to-one function. Then the inverse function of f is the func-

tion g whose rule is

g(y)  x exactly when f (x)  y.

The domain of g is the range of f and the range of g is the domain of f.

EXAMPLE 2

The graph of f (x)  3x  2 is a straight line that certainly passes the Horizontal

Line Test, so f is one-to-one and has an inverse function g. From the definition of

g we know that

g(y)  x exactly when f (x)  y

that is,

g(y)  x exactly when 3x  2  y.

To find the rule of g, we need only solve this last equation for x:

3x  2  y

Add 2 to both sides: 3x  y  2

Divide both sides by 3: x 



y 



Since g(y)  x, we see that the rule of g is g(y) 



y 



. ■

Recall that the letter used for the variable of a function doesn’t matter. For

instance, h(x)  x

and h(t)  t

and h(u)  u

all describe the same function,

whose rule is “square the input.” When dealing with inverse functions, it is cus-

tomary to use the same variable for both f and its inverse g. Consequently, the

inverse function in Example 2 would normally be written as

g(x) 



x 



We can summarize this procedure as follows.

220 CHAPTER 3 Functions and Graphs

Finding Inverse

Functions Algebraically

To find the inverse function of a one-to-one function f :

1. Solve the equation f(x)  y for x.

2. The solution is an expression in y, which is the rule of the inverse func-

tion g, that is, x  g(y).

3. Rewrite the rule of x  g(y) by interchanging x and y.

EXAMPLE 3

Use your calculator to verify that the function f (x)  x

 5 passes the Horizontal

Line Test and hence is one-to-one. Its inverse can be found by solving for x in the

equation x

 5  y:

Subtract 5 from both sides: x

 y  5

Take cube roots on both sides: x  

y  5



Therefore, g( y)  

y  5



is the inverse function of f. Interchanging x and y, we

write this rule as g(x)  

x  5



. ■

EXAMPLE 4

The function f (x)  x  3



is one-to-one, as you can verify with your calculator.

Find its inverse.

SOLUTION We solve the equation:

y  x  3



Square both sides: y

 x  3

Add 3 to both sides: x  y

 3.

Although this last equation is defined for all real numbers y, the original equation

y  x  3



has y  0 (since square roots are nonnegative). In other words, the

range of the function f (the possible values of y) consists of all nonnegative real

numbers. Consequently, the domain of the inverse function g is the set of all non-

negative real numbers, and its rule is

g(y)  y

 3(y  0).

Once again, it’s customary to use the same variable to describe both f and its

inverse function, so we write the rule of g as g(x)  x

 3 (x  0). ■

EXAMPLE 5

In Example 2 of Section 3.6, we considered a water balloon whose volume (in

gallons) was V(x)  x

/55, where x was the radius of the balloon (in inches). This

function is one-to-one because as the radius changes, so does the volume. There-

fore, V(x) has an inverse function. Its rule can be found by solving V  x

/55

for x:

Multiply both sides by 55: 55V  x

Take cube roots of both sides: x  

55V



Since the original function had radius x as input and volume V as output, the

inverse function has volume as input and radius as output. In other words, the in-

verse function allows us to compute the radius of our balloon for any given volume.

For instance, a balloon with a volume of 24 gallons has radius x  







1320



 10.97 inches. ■

EXAMPLE 6

A rule of thumb to figure out how long it would take an investment to double is

the Rule of 72: If i is the interest rate on the investment, then the approximate dou-

bling time is 72/i. If the rate is 10% per year, for example, then it will take ap-

proximately 72/10  7.2 years for the investment to double. (This rule of thumb

is good for interest rates below 20%.)

(a) Let f be the “doubling function” whose rule is f(i)  72/i. Find the rule of the

inverse function g and explain what it represents.

(b) What interest rate is needed to double your investment in 5 years?

SECTION 3.7 Inverse Functions 221

SOLUTION

(a) We solve the equation y  f(i) for i:

y 



iy  72

i 



So the rule of the inverse function is g(y)  72/y.* The function g gives the

interest rate needed to double your money in y years.

(b) Using the inverse function, we see that g(5)  72/5  14.4. We need an in-

terest rate of 14.4% to double our money in 5 years. ■

THE ROUND-TRIP PROPERTIES

The inverse function g of a function f was designed to send each output of f

back to the input it came from. Consequently, if you first apply f and then apply g

to the result, you obtain the number you started with, as illustrated in the next

example.

EXAMPLE 7

As we saw in Example 2, the inverse function of f (x)  3x  2 is

g(x) 



x 



If we start with a number c and apply f, we obtain f (c)  3c  2. If we now apply

g to this result, we obtain

g( f (c))  g(3c  2) 



(3c 

2)  2



 c.

So we are back where we started. Similarly, if we first apply g and then apply f to

a number, we end up where we started:

f (g(c))  f





c 





 3





c 





 2  c.

The function f (x)  x

 5 of Example 3 and its inverse function

g(x)  

x  5



also have these “round-trip” properties. If you apply one function and then the

other, you wind up at the number you started with:

g( f (x))  g(x

 5) 





5)  5







 x

and

f (g(x))  f (



x  5



)  (

x  5



)

 5  (x  5)  5  x. ■

222 CHAPTER 3 Functions and Graphs

*Since the name of the variable doesn’t matter, the rule can be written as g(i)  72/i. Hence, the

doubling function f(i)  72/i is its own inverse. This happens occasionally.

Not only do a function and its inverse have the round-trip properties illus-

trated in Example 7, but somewhat more is true.

Proof By the definition of inverse function,

g(d )  c exactly when f (c)  d.

Consequently, for any c in the domain of f.

g( f (c))  g(d) (because f (c)  d )

 c (because g(d)  c).

A similar argument shows that f (g(d))  d for any d in the domain of g. The last

statement in the Theorem is proved in Exercise 50. ■

EXAMPLE 8

Let

f (x) 



 4



and g(x) 







Show the following:

(a) For every x in the domain of f (that is, all x  2), g( f(x))  x.

(b) For every x in the domain of g (all x  0), f(g(x))  x.

SOLUTION

(a) g( f (x))  g





 4









20  5

(

2x  4)







20  1

x  20



 x.



20 



 4)















 4





 5







 4





SECTION 3.7 Inverse Functions 223

Round-Trip

Theorem

A one-to-one function f and its inverse function g have these properties:

g( f (x))  x for every x in the domain of f ;

f (g(x))  x for every x in the domain of g.

Conversely, if f and g are functions having these properties, then f is one-

to-one and its inverse is g.

(b) f (g(x))  f













x.







4x  5

 4x







 5



 4













 4

By the Round-Trip Theorem, f is a one-to-one function with inverse g. ■

GRAPHS OF INVERSE FUNCTIONS

Finding the rule of the inverse function g of a one-to-one function f by solving the

equation y  f (x) for x, as in the preceding examples, is not always possible (some

equations are hard to solve). But even if you don’t know the rule of g, you can

always find its graph, as shown below.

Suppose f is a one-to-one function and g is its inverse function. Then by the

definition of inverse function:

f (a)  b exactly when g(b)  a.

But f (a)  b means that (a, b) is on the graph of f and g(b)  a means that (b, a)

is on the graph of g. Therefore,

Therefore, the graph of the inverse function g can be obtained by reversing the

coordinates of each point on the graph of f. There are two practical ways of doing

this, each of which is illustrated below.

EXAMPLE 9

Verify that f (x)  .7x

 .3x

 .2x

 2x  .5 has an inverse function g. Use

parametric graphing to graph both f and g.*

SOLUTION First, we graph f in parametric mode by letting

x  t and y  f (t)  .7t

 .3t

 .2t

 2t  .5.

The complete graph in Figure 3–55 shows that f is one-to-one (why?) and hence

has an inverse function g. According to the preceding box, the graph of g can be

obtained by taking each point on the graph of f and reversing its coordinates.

Thus, g can be graphed parametrically by letting

x  f (t)  .7t

 .3t

 .2t

 2t  .5 and y  t.

Figure 3–56 shows the graphs of g and f on the same screen. ■

Figure 3–55 Figure 3–56

⫺5

⫺3

⫺5

⫺3

224 CHAPTER 3 Functions and Graphs

Inverse

Function Graphs

If f is a one-to-one function and g is its inverse function, then

(a, b) is on the graph of f exactly when (b, a) is on the graph of g.

*Parametric graphing is explained in Special Topics 3.3.A.

TECHNOLOGY TIP

The inverse function of y

can be

graphed directly by using this

menu/command:

TI: DRAW/DRAWINV y

Casio: SKETCH/INV

[DRAW is a submenu of the GRAPH

menu on TI-86/89.]

The second method of graphing inverse functions by reversing coordinates

depends on this geometric fact, which is proved in Exercise 49:

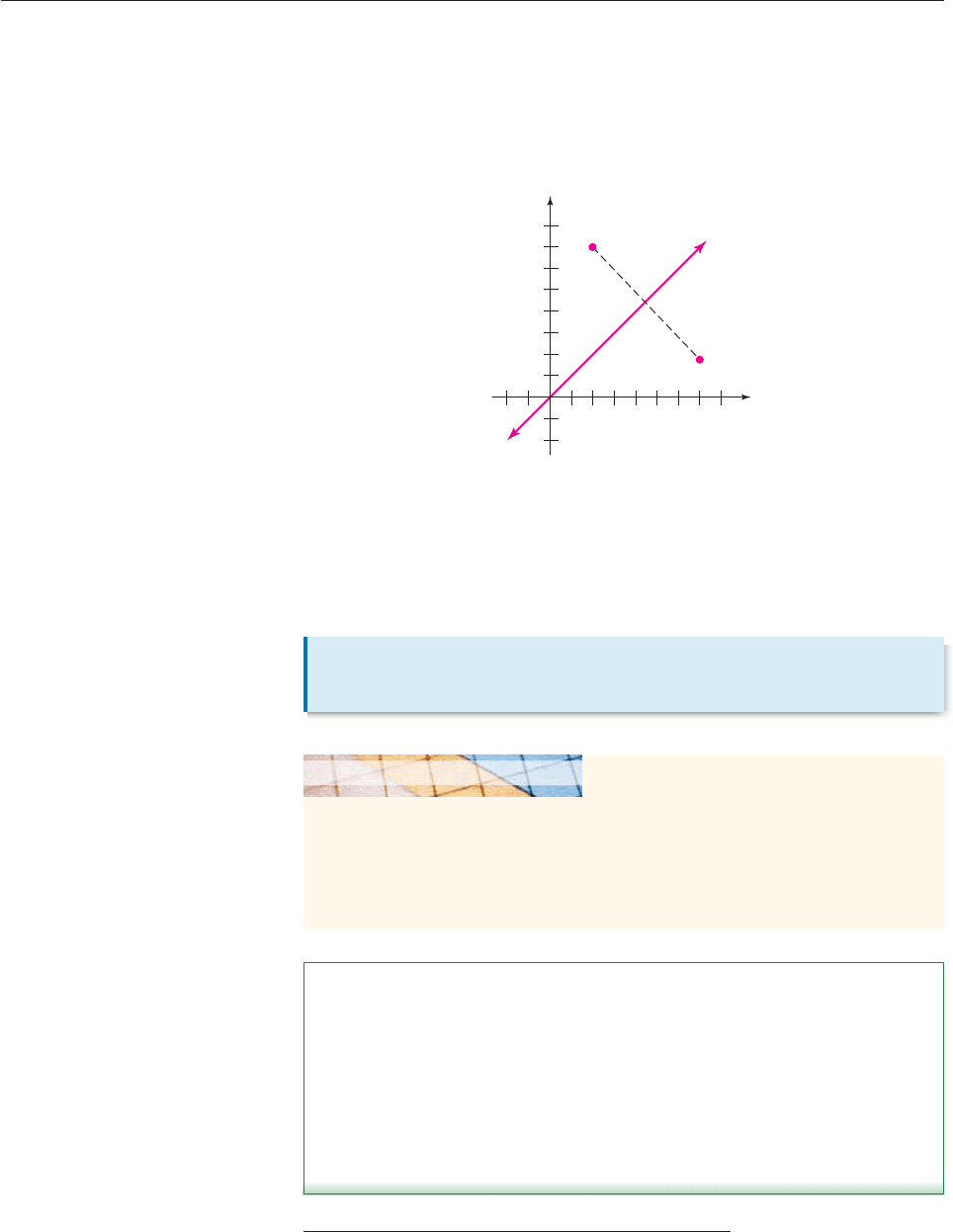
The line y  x is the perpendicular bisector of

the line segment from (a, b) to (b, a),

as shown in Figure 3–57 when a  7, b  2.

SECTION 3.7 Inverse Functions 225

y = x

(7, 2)

(2, 7)

Figure 3–57

Inverse Function

Graphs

If g is the inverse function of f, then the graph of g is the reflection of the

graph of f in the line y  x.

Illustrate this fact by graphing the line y  x, the function

f (x)  x

 5

of Example 3, and its inverse g(x)  

x  5



on the same screen (use a square view-

ing window so that the mirror effect won’t be distorted).

GRAPHING EXPLORATION

NOTE

In many texts, the inverse function of a function f is denoted f

1

. In this notation,

for instance, the inverse of the function f (x)  x

 5 in Example 3 would be written as

1

(x)  

x  5



. Similarly, the reversal properties of inverse functions become

1

(f (x))  x for every x in the domain of f ; and

f (f

1

(x))  x for every x in the domain of f

1

In this context, f

1

does not mean 1/f (see Exercise 45).

*In technical terms, (a, b) and (b, a) are symmetric with respect to the line y  x.

Thus (a, b) and (b, a) lie on opposite sides of y  x, the same distance from it:

They are mirror images of each other, with the line y  x being the mirror.* Con-

sequently, the graph of the inverse function g is the mirror image of the graph of

f. In formal terms,