Hungerford T.W., Shaw D.J. Contemporary Precalculus: A Graphing Approach
Подождите немного. Документ загружается.


236
DISCOVERY PROJECT 3 Feedback—Good and Bad
Whether it’s for a concert or a worship service, a sporting event or a graduation
ceremony, a shopping mall or a lecture hall, audio engineers are concerned to
avoid audio feedback. If the system is not set up correctly, then sound from the
speakers reaches the microphone with enough clarity that it is fed back into the
audio system and amplified. This feedback cycle repeats again and again. Each
time the amplified sound follows very quickly behind the previous one so that the
audience hears an unpleasant hum that rapidly becomes a loud screech. This is
feedback we’d prefer to avoid.
Other types of feedback are considerably more pleasing. Consider, for exam-
ple, an investment of x dollars that earns 4% interest compounded annually. Then
the amount in the account (principal plus interest) after one year is 1.04x. Assume
the initial deposit is left in the account without adding deposits or withdrawing
funds. If $1000 is invested, then the balance (rounded to the nearest penny) is
Beginning 1000
End of year 1 1.04
1000 1040.00
End of year 2 1.04
1040.00 1081.60
End of year 3 1.04
1081.60 1124.86
and so on. You can easily carry out this process on a calculator as follows: key in
1000 and press ENTER; then key in “ 1.04” and press ENTER repeatedly. Each
time you press ENTER, the calculator computes as shown in Figure 1. The result
is an ever-increasing bank balance.
Figure 1
In each of the preceding examples, the output of the process was fed back as
input and the process repeated to generate the result—unpleasant in the first case
and quite pleasant in the second. Now we strip away the specifics and look at the
process in more general terms. Suppose we have a function f and x is in its do-
main. We find f (x) and feed that value back to the function to find f ( f (x)). Then
feed that value back to find f ( f ( f (x))). The sequence of values obtained by con-
tinuing this process
x, f (x), f ( f (x)), f ( f ( f (x))), f ( f ( f ( f (x)))), . . .
is called the orbit of x and the feedback process is called iteration. The functions
themselves ( f, f
2
f f, f
3
f f f, . . .) are called iterates of f.
Tom Sobolik/ Black Star Publishing/PictureQuest

237
Technology makes it easy to compute orbits. For example, let f(x) x
and
enter f as Y
1
in your calculator. Key in 8 and press ENTER. Then key in “STO➡
X : Y
1
” and press ENTER repeatedly.* Each time you press ENTER, the calcula-
tor stores the answer from the preceding calculation as X and evaluates Y
1
at X,
as shown in Figure 2.
Figure 2
Thus, the (approximate) orbit of 8 is
{8, 2.828, 1.682, 1.297, 1.139, 1.067, 1.033, . . .}.
Note that the terms of the orbit are getting closer and closer to 1.
1. Find the orbit of .2 and two other numbers of your choice (except 0 and
1). Do the terms of these orbits get closer and closer to 1?
For the function f (x) x
we can see that f (1) 1, so that iteration pro-
duces the orbit {1, 1, 1, . . .}; we say that 1 is a fixed point for this function. An-
other fixed point is zero because f (0) 0. A fixed point a is called an attracting
fixed point if nearby numbers have orbits that approach a or a repelling fixed
point if nearby numbers have orbits that move farther away from a. The follow-
ing exercises illustrate these ideas for the function f (x) x
.
2. Confirm numerically that 1 is an attracting fixed point by computing the
orbits of .5, 2, and 11.
†
3. Explain mathematically why 1 is an attracting fixed point. [Hint: You
may assume that if u v, then u
v
. Is x
larger or smaller than x
when x 1? When x 1?]
4. Determine whether zero is an attracting fixed point or a repelling fixed
point.
5. Do you think this function has any other fixed points? Why or why not?
Generalizations are interesting in their own right but you may be wondering
whether these ideas have any relevance to the real world. So let’s look at another
*The colon (:) is on the TI and HP-39gs keyboards and in the Casio PRGM menu (press SHIFT VARS).
†
Your calculator may tell you that the terms of the orbits eventually are equal to 1, but this is due to
round-off error.

238
application. Ecologists want to model the growth of the population of some ani-
mal in an ecosystem. To simplify notation, let’s let the variable x represent a frac-
tion of the theoretical maximum population, so that 0 x 1. [If the population
were the maximum the ecosystem could sustain, then x 1 and if there are none
of these animals in the ecosystem, then x 0. We’re interested in the usual situa-
tion where x is somewhere in between.] With a growth rate r, the function f (x)
rx seems to fill the bill.* But logistics, the limitation of resources (food, nesting
locations, etc.), demands an adjustment. The logistic function f (x) rx(1 x)
gives a more realistic model of the growth, which is nearly exponential when x is
small (and 1 x is nearly 0). It also reflects the influence of logistics in that (1 x)
approaches 0 as x approaches 1.
Do these exercises for the logistic function f (x) rx(1 x) and the given
value of r.
6. Use r 2 and different initial values (such as .25, .8, and .1) to confirm
that f (x) 2x(1 x) has fixed point .5.
7. Find the fixed point (to the nearest hundredth) when r
(a) 2.5 (b) 2.8 (c) 3 (d) 3.2
8. Verify that for r 3.3, the orbit of any point x (with 0 x 1) seems
to (eventually) jump back and forth between two values. Somewhere
between 3.2 and 3.3 a bifurcation has occurred. Instead of a single
fixed point we now have a periodic oscillation, with period 2. Find the
two values.
9. Verify that periodic oscillation also occurs when r 3.4. Is the period
still 2?
10. Verify that r 3.5 eventually oscillates among four values (that is,
the period is 4 2
2
). Another bifurcation has occurred. Find the four
values.
11. Verify that for r 3.55 the period is still four but at r 3.56 there are
eight values (period is 8 2
3
). Find them.
12. Is it possible to determine exactly where bifurcations occur? When r is
very large, do you think that the system breaks down to “chaos” or that
there are values of r that have period 2
n
for large values of n?
13. If you are able to consult a naturalist, determine whether some animal
populations follow yearly patterns consistent with the logistic model.
DISCOVERY PROJECT 3
*Notice the similarity to the 4% interest example, where the “balance function” was f (x) 1.04x.
Notice also, that if r is less than 1, the population declines to extinction.
POLYNOMIAL AND RATIONAL FUNCTIONS
Can you afford to go to college?
As you (and your parents) know, the cost of a four-
year college education (tuition, fees, room, board,
books) has steadily increased. It is expected to
continue to do so in the foreseeable future, according
to projections by a large insurance company. This
growth can be modeled by a fourth-degree polynomial
function. See Exercise 46 on page 337.
239
Chapter
© Jeff Greenberg/PhotoEdit
150,000
26
0
0

240
Chapter Outline
Interdependence of
Sections
4.1 Quadratic Functions
4.2 Polynomial Functions
4.2.A Special Topics: Synthetic Division
4.3 Real Roots of Polynomials
4.4 Graphs of Polynomial Functions
4.4.A Special Topics: Polynomial Models
4.5 Rational Functions
4.5.A Special Topics: Other Rational Functions
4.6 Polynomial and Rational Inequalities
4.6.A Special Topics: Absolute Value Inequalities
4.7 Complex Numbers
4.8 Theory of Equations
Polynomial functions arise naturally in many applications. Many compli-
cated functions in applied mathematics can be approximated by polyno-
mial functions or their quotients (rational functions).
4.1 Quadratic Functions*
■ Recognize the algebraic form of a quadratic function.
■ Graph quadratic functions.
■ Find the vertex of a quadratic function graphically and
algebraically.
■ Write the rule of a quadratic function given its vertex and
a point on its graph.
■ Understand the meaning of the vertex as applied to real-world
problems.
A quadratic function is a function whose rule can be written in the form
f (x) ax
2
bx c
for some constants a, b, c, with a 0. The graph of a quadratic function is called
a parabola.
4.1 4.4
4.2 4.3 4.5 4.6
4.7 4.8
*This section may be omitted or postponed if desired. Section 3.4 (Graphs and Transformations) is a
prerequisite for this section.
Section Objectives
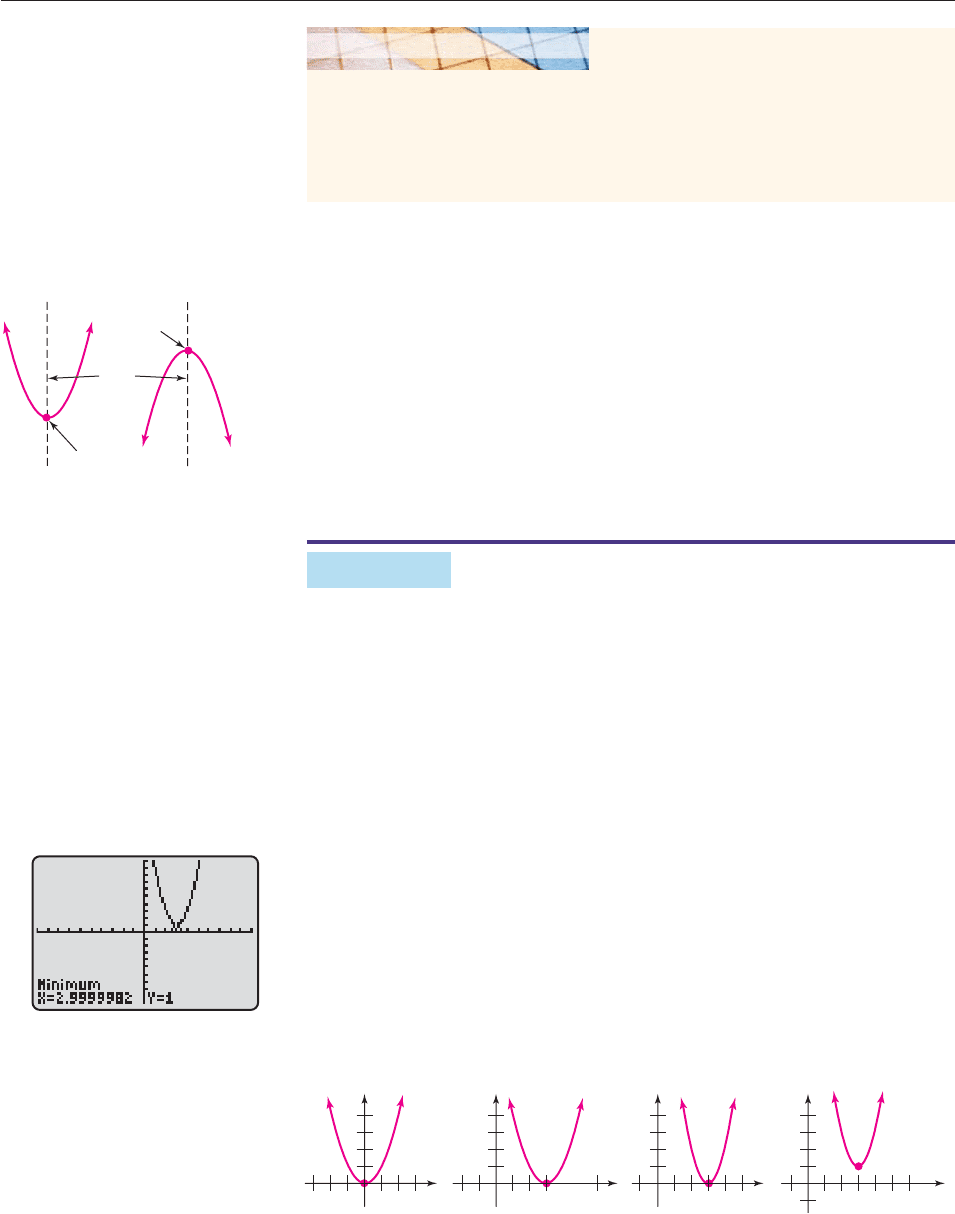
As the Exploration illustrates, all parabolas have the same basic “cup” shape,
though the cup may be broad or narrow. The parabola opens upward when the
coefficient of x
2
is positive and downward when this coefficient is negative.
If a parabola opens upward, its vertex is the lowest point on the graph and if
a parabola opens downward, its vertex is the highest point on the graph, as shown
in Figure 4–1. Every parabola is symmetric with respect to the vertical line
through its vertex; this line is called the axis of the parabola.
Parabolas are easily graphed on a calculator. The vertex can always be ap-
proximated by using the trace feature or a maximum/minimum finder. However,
algebraic techniques can be used to find the vertex precisely and to graph the
parabola.
EXAMPLE 1
Show that the function g(x) 2(x 3)
2
1 is quadratic, graph the function, and
find its vertex.
SOLUTION The function g is quadratic because its rule can be written in the
form g(x) ax
2
bx c:
g(x) 2(x 3)
2
1
2(x
2
6x 9) 1
2x
2
12x 19.
Graphing the function in the standard viewing window (Figure 4–2) and using
the minimum finder, we see that the vertex is approximately (2.999, 1). To find the
vertex exactly, we use the techniques of Section 3.4. The graph of
g(x) 2(x 3)
2
1
can be obtained from the graph of y x
2
as follows:
SECTION 4.1 Quadratic Functions 241
Vertex
Vertex
Axis
Figure 4–1
y = x
2
y = 2(x − 3)
2
+ 1
(0, 0)
(3, 0)
(3, 0)
(3, 1)
1
x
y
y y
y = (x − 3)
2
1
x
y = 2(x − 3)
2
Stretch away from
x-axis by a factor
of 2
Shift the graph
horizontally 3
units to the right
Shift vertically
1 unit upward
1
y
1
x
−1
3
x
Figure 4–3
10
10
−10
−10
Figure 4–2
Using the standard viewing window, graph the following quadratic functions on the
same screen:
f (x) x
2
, f (x) 3x
2
30x 77, f (x) x
2
4x,
f (x) .2x
2
1.5x 5
GRAPHING EXPLORATION

242 CHAPTER 4 Polynomial and Rational Functions
Figure 4–3 shows that when the vertex (0, 0) of y x
2
is shifted 3 units to the
right and 1 unit upward, it moves to (3, 1). Therefore, (3, 1) is the vertex of
g(x) 2(x 3)
2
1. Note how the coordinates of the vertex are related to the
rule of the function g:
Negatives
g(x) 2(x 3)
2
1 vertex (3, 1)
Same ■
The vertex of the function g in Example 1 was easily determined because the
rule of g had a special algebraic form. The vertex of the graph of any quadratic
function can be determined in a similar fashion by first rewriting its rule.
EXAMPLE 2
Find the vertex of the graph of g(x) 3x
2
30x 77 algebraically.
SOLUTION We rewrite the rule of g as follows:
g(x) 3x
2
30x 77
Factor out 3: 3(x
2
10x) 77
Next, we want to complete the square in the expression in parentheses by adding
25 (the square of half the coefficient of x).* In order not to change the rule of the
function, however, we must also subtract 25:
Add 25 25 inside parentheses: 3(x
2
10x 25 25) 77
Use the distributive law: 3(x
2
10x 25) 3
25 77
Simplify: 3(x
2
10x 25) 2
Factor expression in parentheses: 3(x 5)
2
2.
As we saw in Section 3.4, the graph of g(x) is the graph of f (x) x
2
shifted
horizontally 5 units to the left, stretched by a factor of 3, and shifted 2 units
upward, as shown in Figure 4–4. In this process, the vertex (0, 0) of f moves
to (5, 2). Therefore, (5, 2) is the vertex of g(x) 3(x 5)
2
2.
Once again, note how the coordinates of the vertex are related to the rule of the
function.
■
Negatives
g(x) 3(x 5)
2
2 vertex (5, 2)
Same
*Completing the square was discussed on page 22.
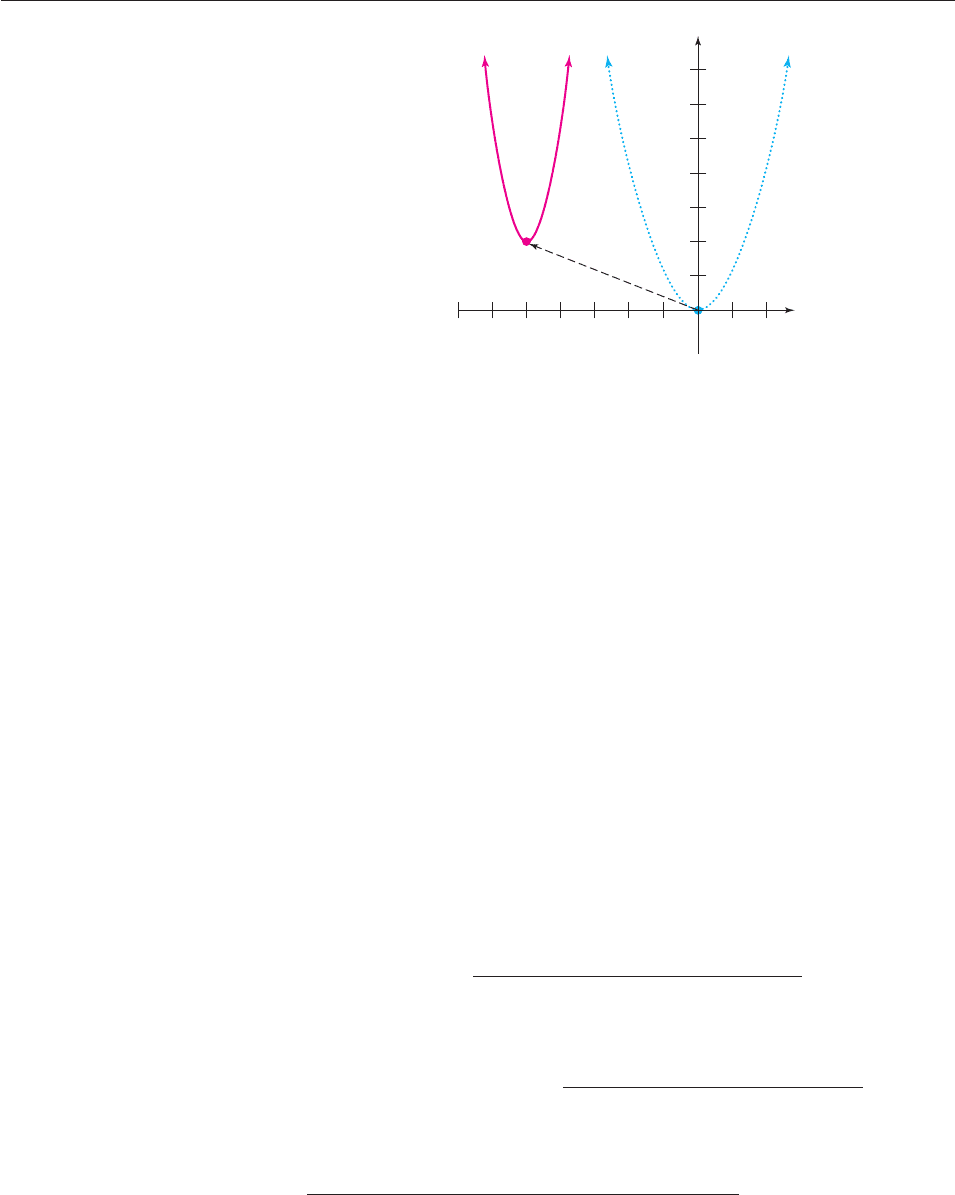
SECTION 4.1 Quadratic Functions 243
The technique used to find the vertex in Example 2 works for any quadratic
function f (x) ax
2
bx c.* First, rewrite the rule of f as follows.
f (x) ax
2
bx c
Factor out a: a
x
2
b
a
x
c
Next, complete the square in the expression in parentheses, as in Example 2. Note
that half the coefficient of x is
2
b
a
and the square of this number is
4
b
a
2
2
.
Add
4
b
a
2
2
4
b
a
2
2
inside parentheses. a
x
2
b
a
x
4
b
a
2
2
4
b
a
2
2
c
Use the distributive law: a
x
2
b
a
x
4
b
a
2
2
a
4
b
a
2
2
c
Simplify and rearrange: a
x
2
b
a
x
4
b
a
2
2
c
4
b
a
2
Factor first expression in parentheses:
†
a
x
2
b
a
2
c
4
b
a
2
.
As in the preceding examples, the graph of f is just the graph of x
2
shifted hori-
zontally, stretched by a factor of a, and shifted vertically. As above, the vertex of
this parabola can be read from the rule of the function:
Negatives
f (x a
x
2
b
a
2
c
4
b
a
2
vertex
2a
b
, c
4
b
a
2
142 43 123
Same
If we let h
2
b
a
and k c
4
b
a
2
, then we have these useful facts.
x
y
2
−5
(0, 0)
(−5, 2)
Figure 4–4
*The following argument is exactly the one used in Example 2, with a in place of 3, b in place of 30,
c in place of 77, and b
2
/4a
2
in place of 25.
†
Verify that this factorization is correct by multiplying out
x
2
b
a
2
.

244 CHAPTER 4 Polynomial and Rational Functions
EXAMPLE 3
Describe the graph of
f (x) x
2
5x 1.
SOLUTION The graph is a downward-opening parabola (because f is a qua-
dratic function and the coefficient of x
2
is negative). According to the preceding
box, the x-coordinate of its vertex is
2
b
a
2(
5
1)
5
2
5
2
2.5.
To find the y-coordinate of the vertex, we need only evaluate f at this number:
f (2.5) (2.5
2
) 5(2.5) 1 7.25.
Therefore, the vertex is (2.5, 7.25). ■
Quadratic
Functions
The rule of the quadratic function f (x) ax
2
bx c can be rewritten
in the form
f (x) a(x h)
2
k,
where h b/2a. The graph of f is a parabola with vertex (h, k). It opens
upward if a 0 and downward if a 0.
Graphically confirm the results of Example 3 by graphing
y x
2
5x 1 and using your maximum finder to approximate the vertex.
CALCULATOR EXPLORATION
EXAMPLE 4
Find the rule of the quadratic function whose graph is a parabola with vertex
(3, 4) that passes through the point (1, 36).
SOLUTION The rule of a quadratic function can be written in the form
f (x) a(x h)
2
k, and its graph is a parabola with vertex (h, k). In this
case, the vertex is (3, 4), so we have h 3 and k 4. Hence, the rule of f is
f (x) a(x 3)
2
4. Since (1, 36) is on the graph, we have
f (1) 36
Substitute 1 for x in the rule of f: a(1 3)
2
4 36
Simplify: 16a 4 36
Subtract 4 from both sides. 16a 32
Divide both sides by 16: a 2.
Therefore, the rule of the function is f (x) 2(x 3)
2
4. ■

SECTION 4.1 Quadratic Functions 245
APPLICATIONS
The solution of many applied problems depends on finding the vertex of a
parabola.
EXAMPLE 5
Find the area and dimensions of the largest rectangular field that can be enclosed
with 3000 feet of fence.
SOLUTION Let x denote the length and y the width of the field, as shown in
Figure 4–5.
Perimeter x y x y 2x 2y
Area xy
Since the perimeter is the length of the fence, 2x 2y 3000. Hence,
2y 3000 2x
and y 1500 x. Consequently, the area is
A xy x(1500 x) 1500x x
2
x
2
1500x.
The largest possible area is just the maximum value of the quadratic function
A(x) x
2
1500x. This maximum occurs at the vertex of the graph of A(x)
(which is a downward-opening parabola because the coefficient of x
2
is negative).
The vertex may be found by using the fact in the box on page 244 (with
a 1 and b 1500):
The x-coordinate of the vertex is
2
1
(
5
0
1
0
)
750 feet.
Hence, the y-coordinate of the vertex, the maximum value of A(x), is
A(750) 750
2
1500
750 562,500 square feet.
It occurs when the length is x 750. In this case the width is
y 1500 x 1500 750 750. ■
x
x
y
y
Figure 4–5
