Hungerford T.W., Shaw D.J. Contemporary Precalculus: A Graphing Approach
Подождите немного. Документ загружается.

When x 3, then the factor x 3 is positive, and the quotient
x
4
x
3
2x
2
6x 21
is also positive (because all its coefficients are). The remainder 64 is also positive.
Therefore, f (x) is positive whenever x 3. In particular, f (x) is never zero when
x 3, and so there are no roots of f (x) greater than 3.
Now we show that g(x) has no root less than 1. Divide g(x) by
x (1) x 1:
112 1031
13225
1 32254
Read off the quotient and remainder and apply the Division Algorithm:
f (x) (x 1)(x
4
3x
3
2x
2
2x 5) 4.
When x 1, then the factor x 1 is negative. When x is negative, its odd pow-
ers are negative and its even powers are positive. Consequently, the quotient
x
4
3x
3
2x
2
2x 5 is positive (because the odd powers of x are multiplied
by negative coefficients). The product of the positive quotient with the negative
factor x 1 is negative. The remainder 4 is also negative. Hence, f (x) is nega-
tive whenever x 1. So there are no real roots less than 1. Therefore, all the
real roots of g(x) lie between 1 and 3.
Finally, we find the roots of g(x) x
5
2x
4
x
3
3x 1. The only possi-
ble rational roots are 1 (why?) and it is easy to verify that neither is actually a root.
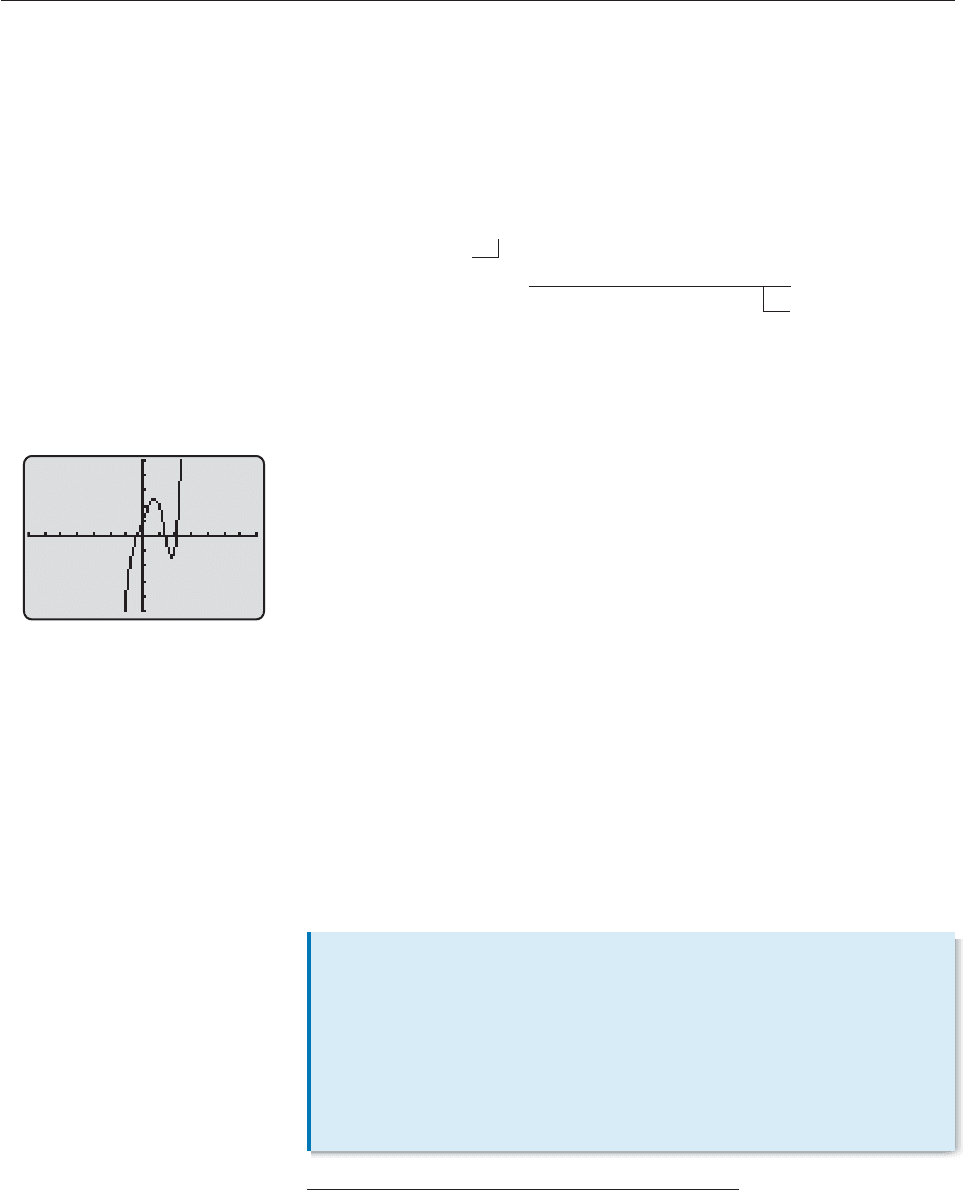
The graph of g(x) in Figure 4–12 shows that there are exactly three real roots (x-
intercepts) between 1 and 3. Since all the real roots of g(x) lie between 1 and 3,
g(x) has only these three real roots. They are readily approximated by a root finder:
x .3361, x 1.4268, and x 2.2012. ■
Suppose f (x) is a polynomial and r and s are real numbers with r s. If all
the real roots of f (x) are between r and s, we say that r is a lower bound and s is an
upper bound for the real roots of f (x).* Example 4 shows that 1 is a lower bound
and 3 is an upper bound for the real roots of g(x) x
5
2x
4
x
3
3x 1.
If you know lower and upper bounds for the real roots of a polynomial, you
can usually determine the number of real roots the polynomial has, as we did in
Example 4. The technique used in Example 4 to test possible lower and upper
bounds works in the general case:
266 CHAPTER 4 Polynomial and Rational Functions
4
4
−4
−4
Figure 4–12
Bounds
Test
Let f (x) be a polynomial with positive leading coefficient.
If d 0 and every number in the last row in the synthetic division of
f (x) by x d is nonnegative,
†
then d is an upper bound for the real
roots of f (x).
If c 0 and the numbers in the last row of the synthetic division of f (x)
by x c are alternately positive and negative [with 0 considered as
either]
‡
then c is a lower bound for the real roots of f (x).
*The bounds are not unique. Any number smaller than r is also a lower bound, and any number larger
than s is also an upper bound.
†
Equivalently, all the coefficients of the quotient and the remainder are nonnegative.
‡
Equivalently, the coefficients of the quotient are altenatively positive and negative, with the last one
and the remainder having opposite signs.
SECTION 4.3 Real Roots of Polynomials 267
NOTE
When the last row of the synthetic divi-
sion by x d is nonnegative, then d is
definitely an upper bound. But if the
last row contains some negative
entries, no conclusion can be drawn
from the Bounds Test [d might or might
not be an upper bound]. In such a case,
try a larger number in place of d.
Analogous remarks apply to lower
bounds.
10
20
−20
−10
5
6
−6
−5
Figure 4–13
Figure 4–14
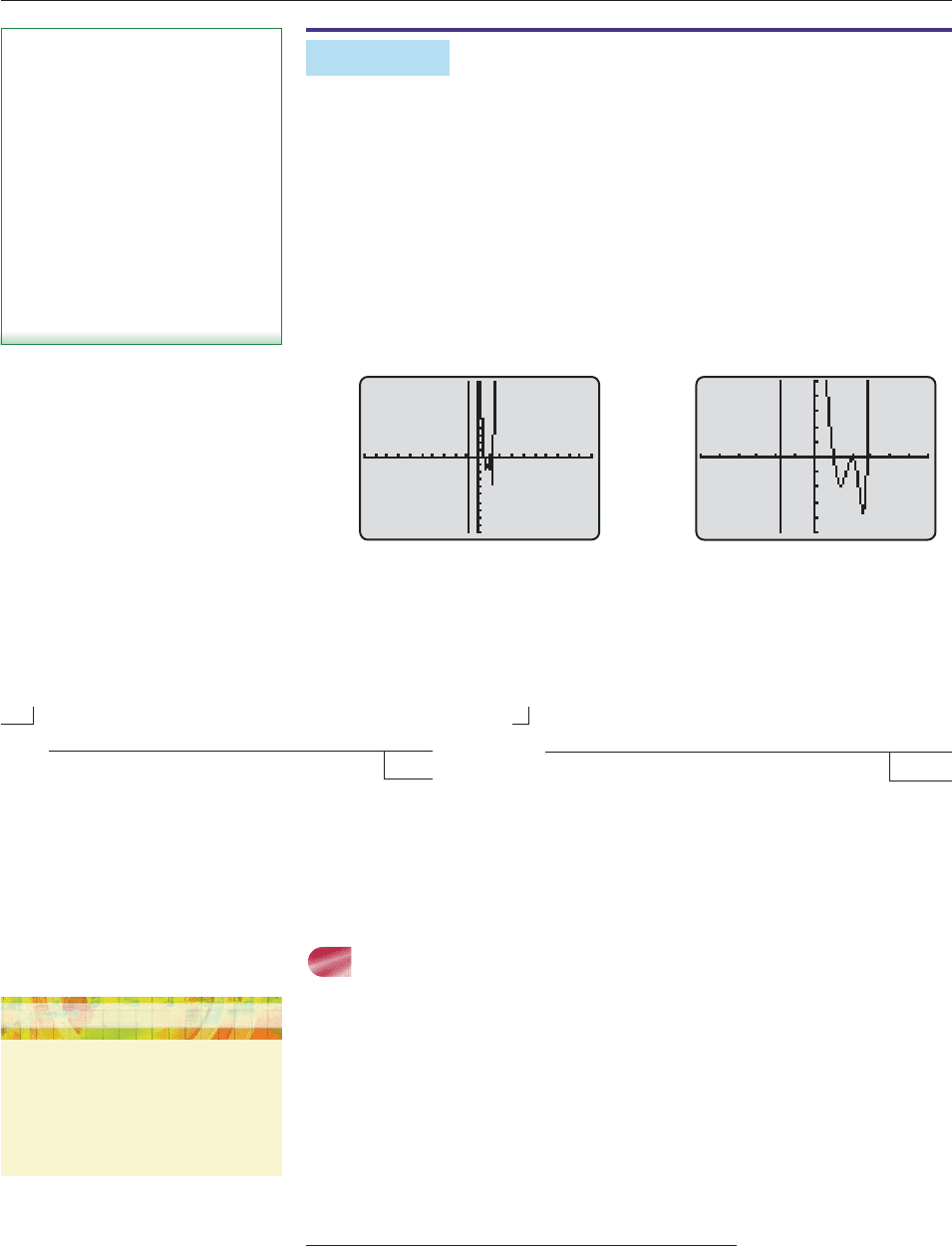
In Figures 4–13 and 4–14, all the real roots of f (x) lie between 2 and 6,
which suggests that these numbers might be lower and upper bounds for the real
roots of f (x).* The Bounds Test shows that this is indeed the case:
2169 728 33 36 20 6 1 69 7 28 33 36 20
21650 86 116 172 272 6 0 54 366 2028 12,366 73,980
1 82543 58 86 136 252 1 0 9 61 338 2061 12,330 74,000
144444444424444444443 144444444424444444443
Alternating Signs All Nonnegative
2 is a lower bound 6 is an upper bound
Therefore, the four x-intercepts in Figure 4–14 are the only real roots of f (x). We
have seen that two of these are the rational roots, 1 and 2. A root finder shows that
the other roots are x 1.7913 and x 2.7913. ■
SUMMARY
The examples above illustrate the following guidelines for finding all the real
roots of a polynomial f (x).
1. Use the Rational Root Test to find all the rational roots of f (x). [Examples
1, 3, 5]
2. Write f (x) as the product of linear factors (one for each rational root) and
another factor g(x). [Examples 2, 3]
3. If g(x) has degree 2, find its roots by factoring or the quadratic formula.
[Example 2]
EXAMPLE 5
Find all real roots of
f (x) x
7
6x
6
9x
5
7x
4
28x
3
33x
2
36x 20.
SOLUTION By the Rational Root Test, the only possible roots are
1, 2, 4, 5, 10, and 20.
The graph of f (x) in Figure 4–13 is hard to read but shows that the possible roots
are quite close to the origin. Changing the window (Figure 4–14), we see that the
only numbers on the list that could possibly be roots (x-intercepts) are 1 and 2.
You can easily verify that both 1 and 2 are roots of f (x).
TECHNOLOGY TIP
The polynomial solvers on TI-86/89
and HP-39gs can find or approximate
all the roots of a polynomial simulta-
neously. The solver on Casio 9850 is
limited to polynomials of degree 2 or 3.
*If you are wondering why we don’t test 3, 4, or 5 as upper bounds, we did—but the Bounds Test is
inconclusive for these numbers, as you can easily verify. See the Note at the top of page.

4. If g(x) has degree 3 or more, use the Bounds Test, if possible, to find lower
and upper bounds for the roots of g(x) and approximate the remaining
roots graphically. [Examples 4, 5]
Shortcuts and variations are always possible. For instance, if the graph of a cubic
shows three x-intercepts, then it has three real roots (the maximum possible) and
there is no point in finding bounds on the roots. In order to find as many roots as
possible exactly in guideline 4, check to see if the rational roots of f (x) are also
roots of g(x) and factor g(x) accordingly, as in Example 3.
268 CHAPTER 4 Polynomial and Rational Functions
EXERCISES 4.3
Directions: When asked to find the roots of a polynomial, find
exact roots whenever possible and approximate the other roots.
In Exercises 1–15, find all the rational roots of the polynomial.
1. x
3
3x
2
x 3 2. x
3
x
2
3x 3
3. x
3
3x
2
6x 8 4. 3x
3
17x
2
35x 25
5. 6x
3
11x
2
19x 6 6. x
4
x
2
2
7. f (x) 2x
5
3x
4
11x
3
6x
2
[Hint: The Rational Root
Test can only be used on polynomials with nonzero constant
terms. Factor f (x) as a product of a power of x and a poly-
nomial g(x) with nonzero constant term. Then use the
Rational Root Test on g(x).]
8. 2x
6
3x
5
7x
4
6x
3
9. f (x)
1
1
2
x
3
1
1
2
x
2
2
3
x 1 [Hint: The Rational Root
Test can only be used on polynomials with integer coeffi-
cients. Note that f(x) and 12f(x) have the same roots (why?).]
10.
1
2
x
4
5
2
x
3
3x
2
2x 4
11.
1
3
x
3
5
6
x
2
1
6
x 1
12.
1
3
x
7
1
2
x
6
1
6
x
5
1
6
x
4
13. .1x
3
1.9x 3 14. .05x
3
.45x
2
.4x 1
15. x
10
10x
9
45x
8
120x
7
210x
6
252x
5
210x
4
120x
3
45x
2
10x 1
In Exercises 16–22, factor the polynomial as a product of lin-
ear factors and a factor g(x) such that g(x) is either a constant
or a polynomial that has no rational roots.
16. x
15
x 1 17. 2x
3
2x
2
3x 3
18. 12x
3
10x
2
6x 2 19. x
6
4x
5
3x
4
12x
3
20. x
5
2x
4
2x
3
3x 2
21. x
5
6x
4
5x
3
34x
2
84x 56
22. x
5
4x
3
x
2
6x
In Exercises 23–28, use the Bounds Test to find lower and
upper bounds for the real roots of the polynomial.
23. x
3
2x
2
7x 20 24. x
3
15x
2
16x 12
25. x
3
5x
2
5x 3 26. x
4
2x
3
3x
2
4x 4
27. x
5
5x
4
9x
3
18x
2
68x 176 [Hint: The Bounds
Test applies only to polynomials with positive leading coef-
ficient. The polynomial f (x) has the same roots as f (x)
(why?).]
28. .002x
3
5x
2
8x 3
In Exercises 29–40, find all real roots of the polynomial.
29. 2x
3
x
2
13x 6 30. t
4
3t
3
5t
2
9t 6
31. 6x
3
13x
2
x 2 32. z
3
z
2
2z 2
33. x
4
x
3
19x
2
32x 12
34. 3x
6
7x
5
22x
4
8x
3
35. 2x
5
x
4
10x
3
5x
2
12x 6
36. x
10
10x
9
45x
8
120x
7
210x
6
252x
5
210x
4
120x
3
45x
2
10x 1
37. x
6
3x
5
4x
4
9x
2
27x 36
38. x
5
8x
4
20x
3
9x
2
27x 27
39. x
4
48x
3
101x
2
49x 50
40. 3x
7
8x
6
13x
5
36x
4
10x
3
21x
2
41x 10
41. (a) Show that 2
is an irrational number. [Hint: 2
is a root
of x
2
2. Does this polynomial have any rational roots?]
(b) Show that 3
is irrational.
(c) What would happen if you tried to use the techniques
from the previous parts of this question to show 4
is
irrational?
42. Graph f (x) .001x
3
.199x
2
.23x 6 in the standard
viewing window.
(a) How many roots does f (x) appear to have? Without
changing the viewing window, explain why f (x) must
have an additional root. [Hint: Each root corresponds to
a factor of f (x). What does the rest of the factorization
consist of?]
(b) Find all the roots of f (x).
43. According to data from the FBI, the number of people mur-
dered each year per 100,000 can be approximated by the
polynomial function

f(x) .0002724x
5
.005237x
4
.03027x
3
.1069x
2
.9062x 9.003
(0 x 10)
where x 0 corresponds to 1995.
(a) What was the murder rate in 2000 and in 2003?
(b) According to this model, in what year was the murder
rate 7 people per 100,000?
(c) According to this model, in what year between 1995
and 2005 was the murder rate the highest?
(d) According to this model, in what year between 1995
and 2005 was the murder rate the lowest? (Be careful!
This one isn’t immediate.)
(e) According to this model, during what time interval
between 1995 and 2005 was the murder rate increasing?
44. During the first 150 hours of an experiment, the growth rate
of a bacteria population at time t hours is
g(t) .0003t
3
.04t
2
.3t .2 bacteria per hour.
(a) What is the growth rate at 50 hours? At 100 hours?
(b) What is the growth rate at 145 hours? What does this
mean?
(c) At what time is the growth rate 0?
(d) At what time is the growth rate 50 bacteria per hour?
(e) At what time does the highest growth rate occur?
45. An open-top reinforced box is to be made from a 12- by
36-inch piece of cardboard by cutting along the marked
lines, discarding the shaded pieces, and folding as shown in
the figure. If the box must be less than 2.5 inches high, what
size squares should be cut from the corners in order for the
box to have a volume of 448 cubic inches?
46. A box with a lid is to be made from a 48- by 24-inch piece
of cardboard by cutting and folding, as shown in the figure.
If the box must be at least 6 inches high, what size squares
should be cut from the two corners in order for the box to
have a volume of 1000 cubic inches?
xx x
xx
24
48
xx xx
xx
12
36
cut along fold along
SECTION 4.3 Real Roots of Polynomials 269
47. In a sealed chamber where the temperature varies, the in-
stantaneous rate of change of temperature with respect to
time over an 11-day period is given by
F(t) .0035t
4
.4t
2
.2t 6,
where time is measured in days and temperature in
degrees Fahrenheit (so that rate of change is in degrees
per day).
(a) At what rate is the temperature changing at the begin-
ning of the period (t 0)? At the end of the period
(t 11)?
(b) When is the temperature increasing at a rate of 4°F
per day?
(c) When is the temperature decreasing at a rate of 3°F
per day?
(d) When is the temperature decreasing at the fastest
rate?
48. (a) If c is a root of
f (x) 5x
4
4x
3
3x
2
4x 5,
show that 1/c is also a root.
(b) Do part (a) with f (x) replaced by
g(x) 2x
6
3x
5
4x
4
5x
3
4x
2
3x 2.
(c) Let f (x) a
12
x
12
a
11
x
11
a
2
x
2
a
1
x a
0
.
What conditions must the coefficients a
i
satisfy in order
that this statement be true: If c is a root of f (x), then 1/c
is also a root?
49. According to the “modified logistic growth” model, the rate
at which a population of bunnies grows is a function of x,
the number of bunnies there already are:
f(x) k(x
3
x
2
(T C) CTx) bunnies/year
where C is the “carrying capacity” of the bunnies’ environ-
ment, T is the “threshold population” of bunnies necessary
for them to thrive and survive, and k is a positive constant
that can be determined experimentally. If f (x) is big, that
means the bunny population is growing quickly. If f (x) is
negative, it means the bunny population is declining.
(a) Why can we assume T C?
(b) What is happening to the bunny population if x is
between T and C?
(c) What is happening to the bunny population if x T?
(d) What is happening to the bunny population if x C?
(e) Factor k(x
3
x
2
(T C) CTx)
(f) What bunny populations will remain stable (un-
changing)?
■ Understand the properties of the graph of a polynomial.
■ Find a complete graph of a polynomial.
■ Use polynomial graphs in applications.
The graphs of first- and second-degree polynomial functions are straight lines and
parabolas respectively (Sections 1.4 and 4.1). What happens when the degree is
higher?
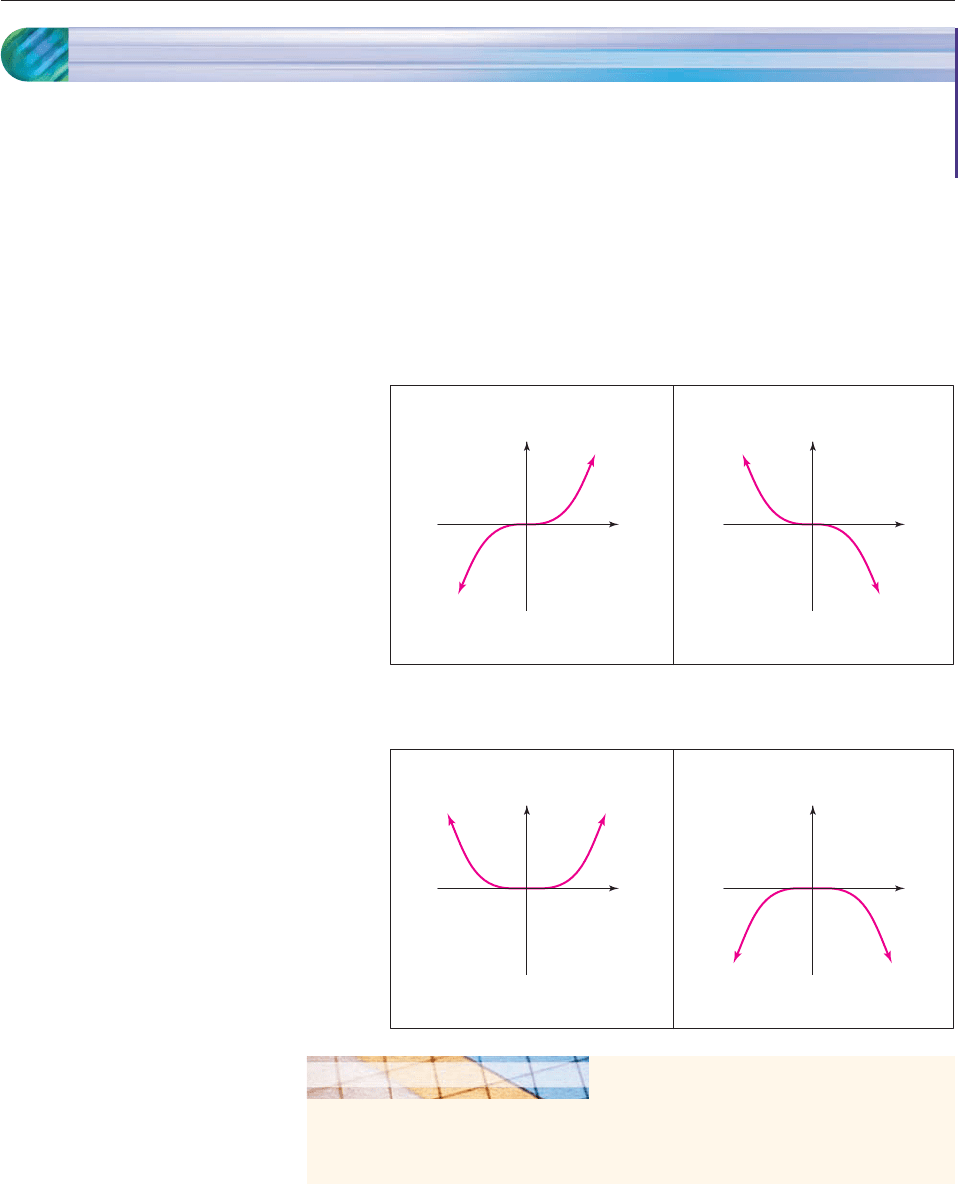
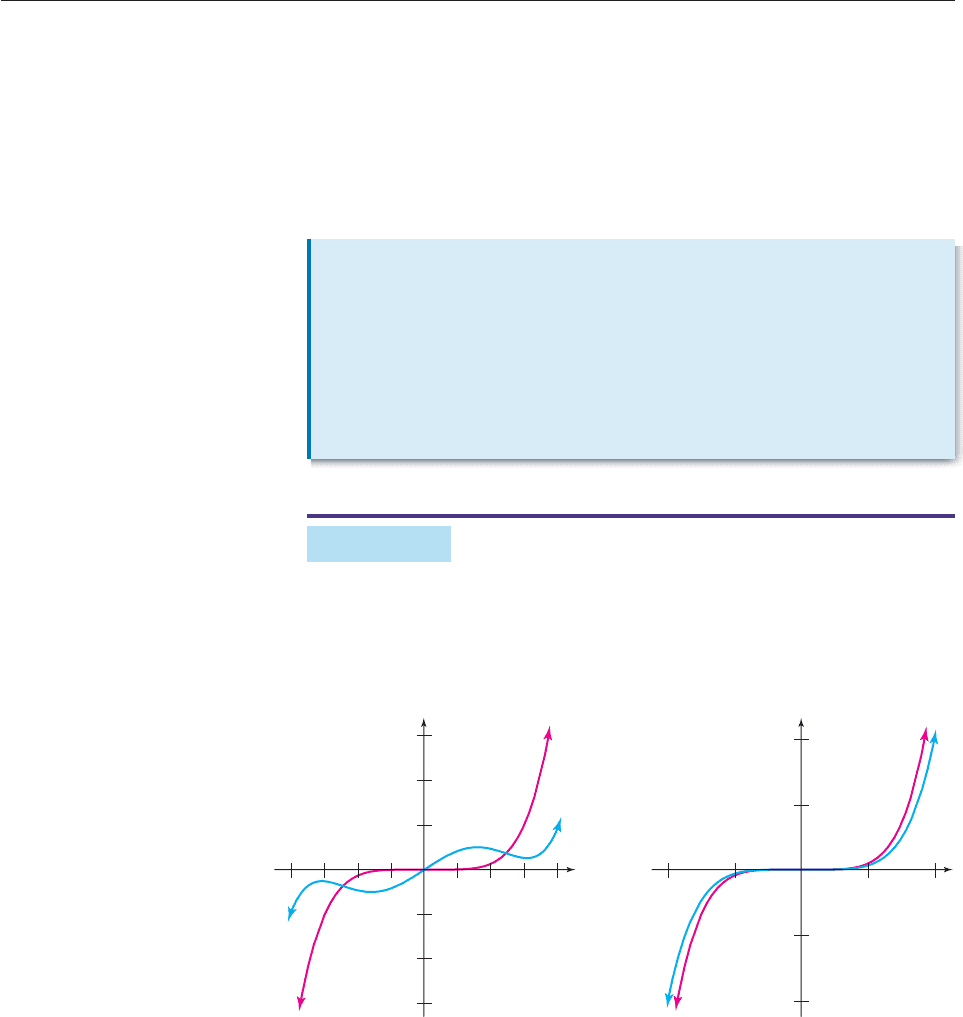
The simplest polynomial functions are those of the form f (x) ax
n
(where a
is a constant). Their graphs are of four types, as shown in the following chart.
GRAPH OF f(x) ax
n
270 CHAPTER 4 Polynomial and Rational Functions
4.4 Graphs of Polynomial Functions
Examples: f(x) 2x
3
g(x) .01x
5
a is positive
Examples: f(x) x
3
g(x) 2x
7
x
y
a is negative
x
y
Examples: f(x) 2x
4
g(x) 2x
6
a is positive
n even
n odd
Examples: f(x) 2x
2
g(x) 3x
4
x
y
a is negative
x
y
Verify the accuracy of the preceding summary by graphing each of the examples in
the window with 5 x 5 and 30 y 30. What effect does increasing the
value of n have on these graphs?
GRAPHING EXPLORATION
Section Objectives
The graphs of more complicated polynomial functions can vary considerably in
shape. Understanding the properties discussed below should assist you to interpret
screen images correctly and to determine when a polynomial graph is complete.
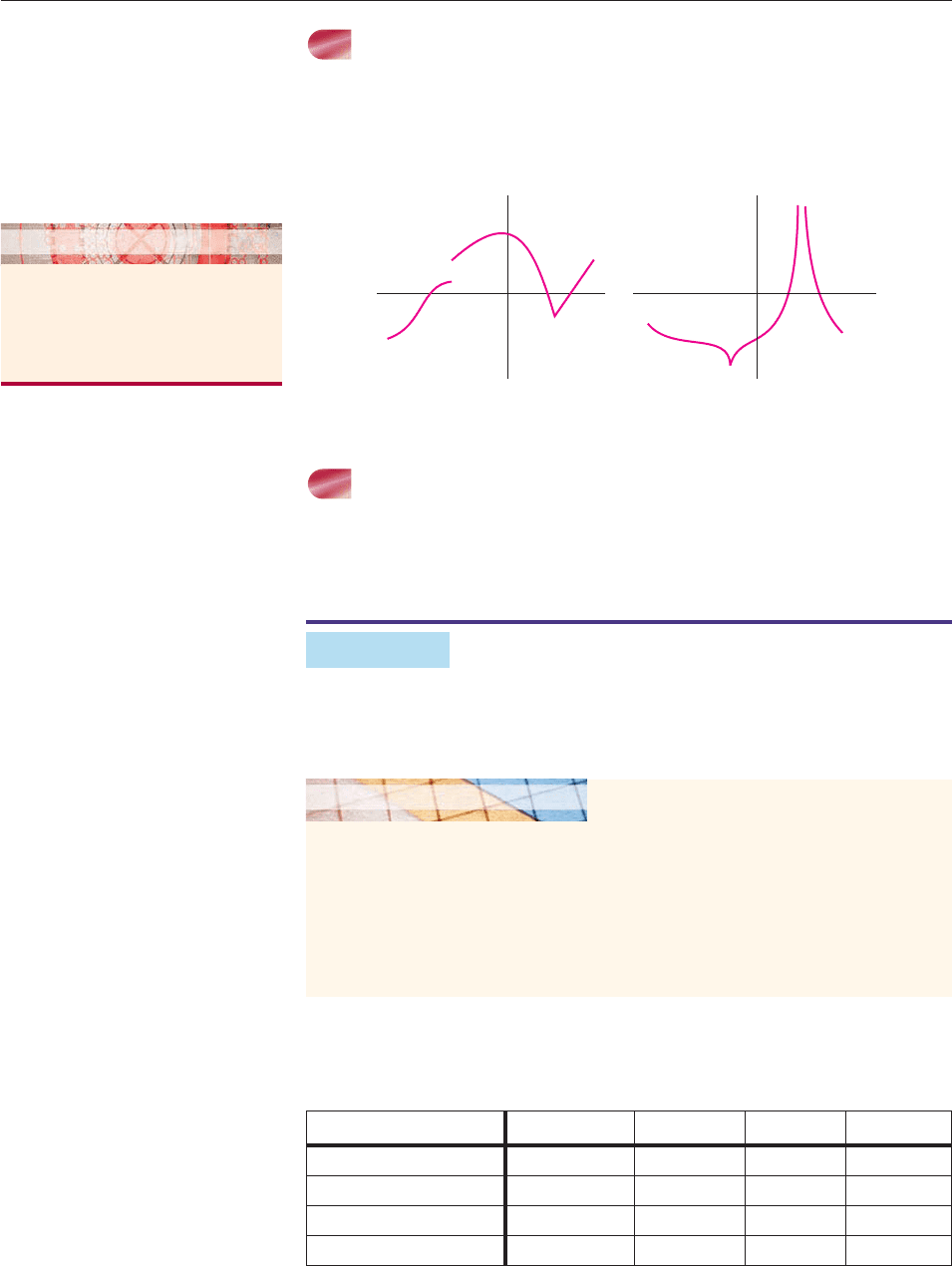
CONTINUITY
Every polynomial graph is continuous, meaning that it is an unbroken curve,
with no jumps, gaps, or holes. Furthermore, polynomial graphs have no sharp
corners. Thus, neither of the graphs in Figure 4–15 is the graph of a polynomial
function.
SECTION 4.4 Graphs of Polynomial Functions 271
Using the standard viewing window, graph f and g on the same screen.
Do the two graphs look different? Now graph f and g in the viewing window with
20 x 20 and 10,000 y 10,000. Do the graphs look almost the same?
Finally, graph f and g in the viewing window with
100 x 100 and 1,000,000 y 1,000,000.
Do the graphs look virtually identical?
GRAPHING EXPLORATION
Sharp
corner
Sharp
corner
Gap
Jump
Figure 4–15
SHAPE OF THE GRAPH WHEN x IS LARGE
The shape of a polynomial graph at the far left and far right of the coordinate
plane is easily determined by using our knowledge of graphs of functions of the
form f (x) ax
n
.
EXAMPLE 1
Consider the function f (x) 2x
3
x
2
6x and the function determined by its
leading term g(x) 2x
3
.
The reason the answer to the last question is “yes” can be understood from this
table.
x 100 50 70 100
6x 600 300 420 600
x
2
10,000 2,500 4,900 10,000
g(x) 2x
3
2,000,000 250,000 686,000 2,000,000
f (x) 2x
3
x
2
6x 1,989,400 247,200 690,480 2,009,400
CAUTION
On a calculator screen a polynomial
graph may look like a series of
juxtaposed line segments, rather than
a smooth, continuous curve.
It shows that when x is large, the terms x
2
and 6x are insignificant compared
with 2x
3
and barely affect the value of f (x). Hence, the values of f (x) and g(x) are
relatively close. ■
Example 1 is typical of what happens in every case: When x is very large,
the highest power of x totally overwhelms all lower powers and plays the greatest
role in determining the value of the function.
272 CHAPTER 4 Polynomial and Rational Functions
Behavior When
x Is Large
When x is very large, the graph of a polynomial function closely resem-
bles the graph of its highest degree term.
In particular, when the polynomial function has odd degree, one end of its
graph shoots upward and the other end downward.
When the polynomial function has even degree, both ends of its graph
shoot upward or both ends shoot downward.
EXAMPLE 2
Graph f (x)
1
x
2
5
0
x
6
3
x and g(x)
1
x
2
5
0
on the same axes, first using the
window 4 x 4 and then using the window 12 x 12 (Figure 4–16).
−4
−6
2
g(x)
f(x)
1
0
43
−2 −1−3−4
−2
2
4
6
x
y
6
g(x)
f(x)
0
(b)(a)
12
−6−12
−1000
−2000
1000
2000
x
y
Figure 4–16
Notice how the first window shows that these are very different functions, but the
second window shows that as |x| gets larger, the graph of
1
x
2
5
0
x
6
3
x closely
resembles the graph of
1
x
2
5
0
. If you were to graph these functions on the interval
1000 x 1000, you would be hard pressed to tell the difference between
these curves. ■
EXAMPLE 3
It is a fact that x
4
2x
3
3x
2
4x 4 (x 1)
2
(x 2)
2
. Use this fact to
sketch the graph of
f(x) x
4
2x
3
3x
2
4x 4
SOLUTION f has double roots at x 1 and x 2 . The leading coefficient is
negative and even, which tells us that both ends of the graph shoot downward. We
find the y-intercept by observing that f (0) 4. We obtain the graph shown in
Figure 4–18 on the next page. ■
SECTION 4.4 Graphs of Polynomial Functions 273
x-INTERCEPTS
As we saw in Section 4.3, the x-intercepts of the graph of a polynomial function
are the real roots of the polynomial. Since a polynomial of degree n has at most n
distinct roots (page 257), we have the following fact.
x-Intercepts
The graph of a polynomial function of degree n meets the x-axis at most
n times.
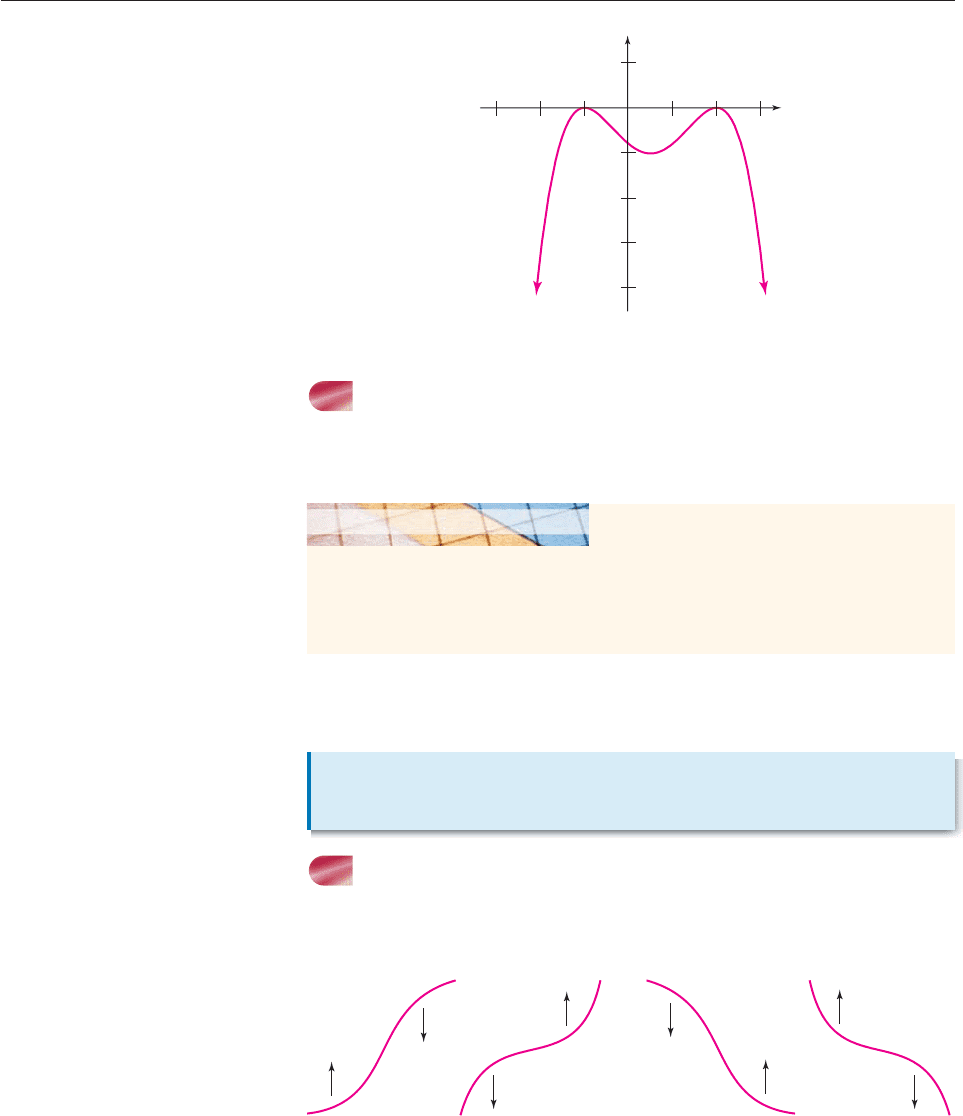
There is another connection between roots and graphs. For example, it is easy
to see that the roots of
f (x) (x 3)
2
(x 1)(x 1)
3
are 3, 1, and 1. We say that
3 is a root of multiplicity 2;
1 is a root of multiplicity 1;
1 is a root of multiplicity 3.
Observe that the graph of f (x) in Figure 4–17 does not cross the x-axis at
3 (a root whose multiplicity is an even number) but does cross the
x-axis at 1 and 1 (roots of odd multiplicity).
30
3
−5
−12
Figure 4–17
Multiplicity
and Graphs
Let c be a root of multiplicity k of a polynomial function f.
If k is odd, the graph of f crosses the x-axis at c.
If k is even, the graph of f touches, but does not cross, the x-axis at c.
More generally, a number c is a root of multiplicity k of a polynomial f (x) if (x c)
k
is a factor of f (x) and no higher power of (x c) is a factor, and we have this fact.
LOCAL EXTREMA
The term local extremum (plural, extrema) refers to either a local maximum or a
local minimum, that is, a point where the graph is a peak or a valley.
274 CHAPTER 4 Polynomial and Rational Functions
−10
−15
−20
21
0
3
−2 −1−3
−5
5
x
y
Figure 4–18
Graph f (x) x
3
2x
2
4x 3 in the standard viewing window. What is the total
number of peaks and valleys on the graph? What is the degree of f (x)?
Now graph g(x) x
4
3x
3
2x
2
4x 5 in the standard viewing window.
What is the total number of peaks and valleys on the graph? What is the degree of g(x)?
GRAPHING EXPLORATION
The two polynomials you have just graphed are illustrations of the following
fact, which is proved in calculus.
Local
Extrema
A polynomial function of degree n has at most n 1 local extrema. In other
words, the total number of peaks and valleys on the graph is at most n 1.
BENDING
A polynomial graph may bend upward or downward as indicated here by the ver-
tical arrows (Figure 4–19):
Figure 4–19
A point at which the graph changes from bending downward to bending upward
(or vice versa) is called a point of inflection. The direction in which a graph
bends may not always be clear on a calculator screen, and calculus is usually
required to determine the exact location of points of inflection. The number of
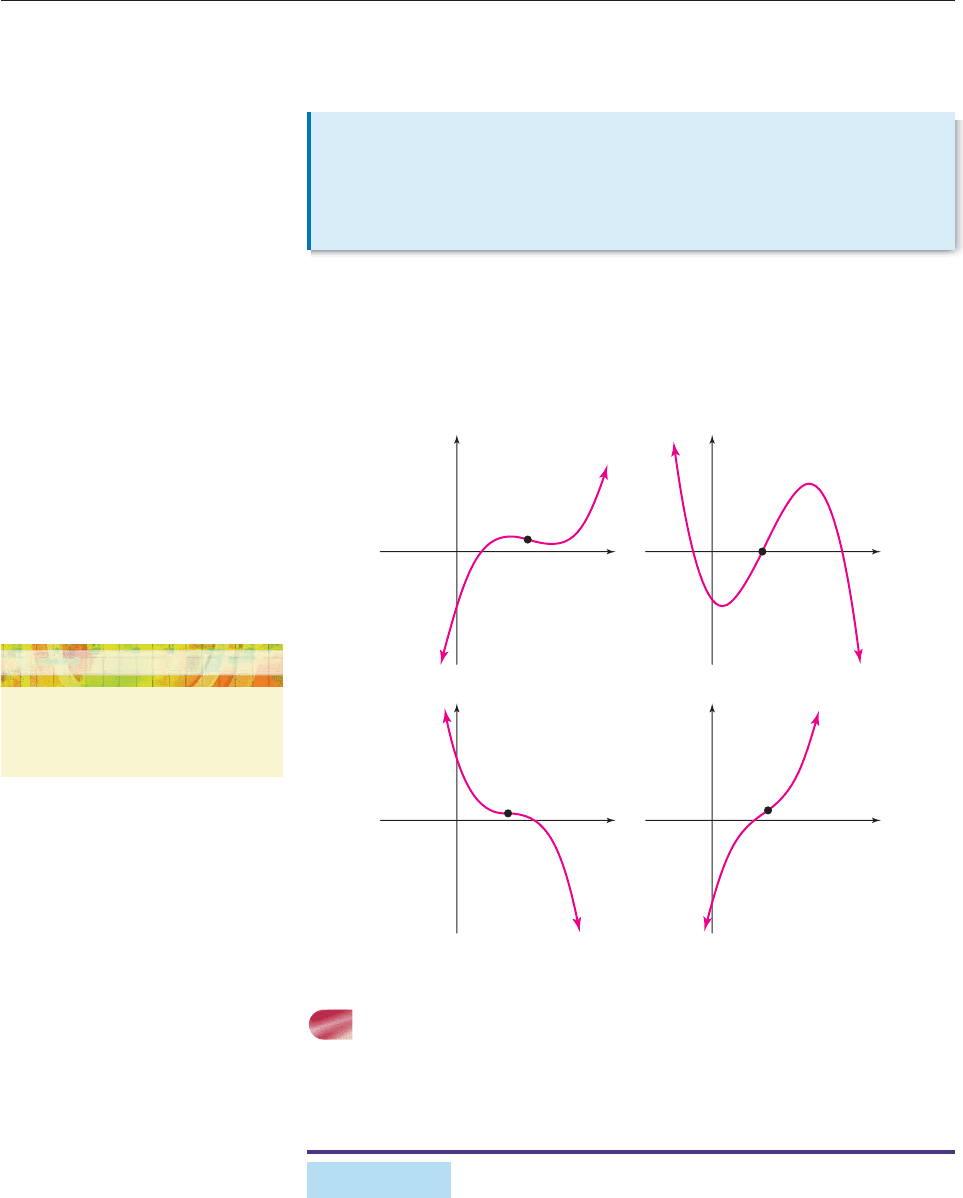
inflection points and hence the amount of bending in the graph are governed by
these facts, which are proved in calculus.
SECTION 4.4 Graphs of Polynomial Functions 275
Points
of Inflection
The graph of a polynomial function of degree n (with n 2) has at most
n 2 points of inflection.
The graph of a polynomial function of odd degree n (with n 3) has at
least one point of inflection.
Thus, the graph of a quadratic function (degree 2) has no points of inflection
(n 2 2 2 0), and the graph of a cubic has exactly one (since it has at least
one and at most 3 2 1). Figure 4–20 shows several cubic graphs, with their
inflection point marked.
TECHNOLOGY TIP
Points of inflection may be found by
using INFLC in the TI-86/89 GRAPH
MATH menu.
x x
y
y
x x
y
y
Figure 4–20
COMPLETE GRAPHS OF POLYNOMIAL FUNCTIONS
By using the facts discussed earlier, you can often determine whether or not the
graph of a polynomial function is complete (that is, shows all the important
features).
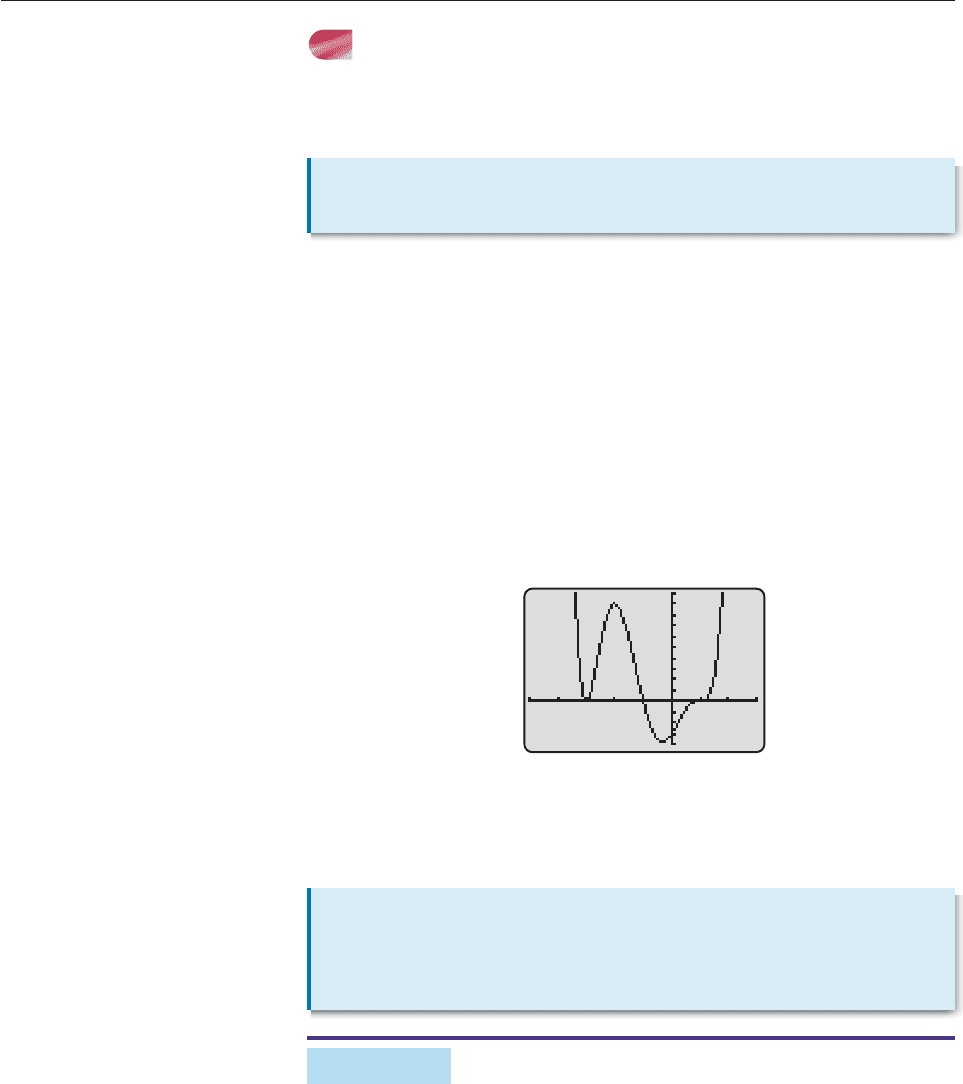
EXAMPLE 4
Find a complete graph of
f (x) x
4
10x
3
21x
2
40x 80.
