Hungerford T.W., Shaw D.J. Contemporary Precalculus: A Graphing Approach
Подождите немного. Документ загружается.


SOLUTION
(a) When x is very large, a polynomial function behaves in essentially the same
way as its highest degree term, as we saw on page 272. Consequently, we
have this approximation:
f (x)
7x
4
2x
4
6
x
3
x
2
4
7
2
x
x
4
4
7
2
3.5.
Thus, when x is large, the graph of f (x) is very close to the horizontal line
y 3.5, which is a horizontal asymptote of the graph.
296 CHAPTER 4 Polynomial and Rational Functions
Confirm the last statement by graphing f (x) and y 3.5 in the window with
10 x 10 and 2 y 12.
GRAPHING EXPLORATION
(b) When x is large, the graph of g closely resembles the graph of
y
x
x
2
3
1
x
.
By the Big-Little Principle, 1/x is very close to 0 when x is large. So the
line y 0 (that is, the x-axis) is the horizontal asymptote.
(c) When x is large, the graph of g closely resembles the graph of
y
2
x
x
3
2x
2
In this case the Big-Little principle doesn’t help us; when x is large, so is
2x
2
. So all we know is that h(x) eventually resembles the graph of 2x
2
. Special
Topics 4.5.A discusses this case in more detail. ■
Arguments similar to those in the preceding example, using the highest-
degree terms in the numerator and denominator, carry over to the general case and
lead to this conclusion.
GRAPHS OF RATIONAL FUNCTIONS
The procedure for finding accurate graphs of rational functions is summarized
here.
Horizontal
Asymptotes
Let f (x)
a
cx
x
k
n
be a rational function whose numerator has degree n
and whose denominator has degree k.
If n k, then the line y a/c is a horizontal asymptote.
If n k, then the x-axis (the line y 0) is a horizontal asymptote.
If n k, then there is no horizontal asymptote.

EXAMPLE 5
If you ignore the preceding advice and simply graph f (x)
x
2
x
x
1
6
in the
standard viewing window, you get garbage (Figure 4–42). So let’s try analyzing
the function. We begin by factoring.
f (x)
x
2
x
x
1
6
(x
x
2
)(x
1
3)
.
The factored form allows us to read off the necessary information:
Vertical Asymptotes: x 2 and x 3 (roots of the denominator but not of
the numerator).
Horizontal Asymptote: x-axis (because denominator has larger degree than
the numerator).
Intercepts: y-intercept at f (0)
0
2
0
0
1
6
1
6
; x-intercept at x 1 (root
of the numerator but not of the denominator).
Interpreting Figure 4–42 in light of this information suggests that a complete
graph of f looks something like Figure 4–43.
SECTION 4.5 Rational Functions 297
Graphing f(x)
g
h
(
(
x
x
)
)
When
Degree g(x) X Degree h(x)
1. Analyze the function algebraically to determine its vertical asymptotes,
holes, and intercepts.
2. Determine the horizontal asymptote of the graph when x is large by
using the facts in the box on the opposite page.
3. Use the preceding information to select an appropriate viewing window
(or windows), to interpret the calculator’s version of the graph (if
necessary), and to sketch an accurate graph.
10
10
−10
−10
Figure 4–42
x
y
2
1
4
3
6
5
−1
−2
−3
−4
−5
−1−2123
4
Figure 4–43

EXAMPLE 6
Graph
f (x)
x
3
2
x
x
2
3
2x
SOLUTION
We factor and then read off the necessary information:
f (x)
x
3
2
x
x
2
3
2x
x(x
2
2
x
)(
3
x 1)
.
Hole: x 0 (root of multiplicity 3 in the denominator and a root of multipli-
city 1 in the numerator; see page 295).
Vertical Asymptotes: x 2 and x 1 (roots of denominator that are not
also roots of numerator).
Horizontal Asymptote: y 2/1 2 (because numerator and denominator
have the same degree; see the box on page 296).
Intercepts None: There is no x-intercept at 0, because even though x 0 is a
root of the numerator, it is also a root of the denominator. So f(0) is not defined
and there is no y-intercept.
Using this information and selecting a decimal viewing window that will accu-
rately portray the graph near the vertical asymptotes, we obtain what seems to be
a reasonably complete graph in Figure 4–44. The graph does not show the hole at
x 0. Also, the graph appears to be falling to the right of x 1 as it approaches
its horizontal asymptote, but this is not the case.
298 CHAPTER 4 Polynomial and Rational Functions
Find a viewing window in which the graph of f looks similar to Figure 4–43. The
Technology Tip in the margin may be helpful.
■
GRAPHING EXPLORATION
NOTE
The graph of a rational function never touches a horizontal asymptote when x is large in absolute
value. For smaller values of x, however, the graph may cross the asymptote, as in Example 5.
TECHNOLOGY TIP
A decimal window (with the y-range
suitably adjusted) will usually produce
an accurate graph of a rational func-
tion whose vertical asymptotes occur
at numbers such as x 2.0 or 3.7
or 4.1 that are within the x-range.
Graph f in this same viewing window and use the trace feature, beginning at approx-
imately x 1.1 and moving to the right. For what values of x is the graph above the
horizontal asymptote y 2? For what values of x is the graph below the horizontal
asymptote?
GRAPHING EXPLORATION
The exploration indicates that there is some hidden behavior of the graph that is
not visible in Figure 4–44.
8
4.7
−4.7
−6
Figure 4–44
This Exploration shows that the graph has a local minimum near x 4 and
then stays below the asymptote, moving closer and closer to it as x takes larger
values. ■
APPLICATIONS
Several applications of rational functions were considered in Section 2.4. Here is
another one.
EXAMPLE 7
A cardboard box with a square base and a volume of 1000 cubic inches is to be
constructed (Figure 4–45). The box must be at least 2 inches in height.
(a) What are the possible lengths for a side of the base if no more than 1100
square inches of cardboard can be used to construct the box?
(b) What is the least possible amount of cardboard that can be used?
(c) What are the dimensions of the box that uses the least possible amount of
cardboard?
SOLUTION The amount of cardboard needed is given by the surface area S of
the box. From Figure 4–45, we have
S
area of area of area of each
top bottom side
S x
2
x
2
xh xh xh xh 2x
2
4xh.
Since the volume of the box is given by
Length Width Height Volume,
we have
x
x
h 1000 or, equivalently, h
10
x
0
2
0
.
Substituting the above into the surface area formula allows us to express the sur-
face area as a function of one variable, x:
S(x) 2x
2
4xh 2x
2
4x
10
x
0
2
0
2x
2
40
x
00
2x
3
x
4000
.
Although the rational function S(x) is defined for all nonzero real numbers, x is a
length here and must be positive. Furthermore, x
2
500 because if x
2
500,
then h
10
x
0
2
0
would be less than 2, contrary to specifications. Hence, the only
values of x that make sense in this context are those with 0 x 500
. Since
500
22.4, we choose the viewing window in Figure 4–46. For each point
SECTION 4.5 Rational Functions 299
To see this hidden behavior, graph both f and the line y 2 in the viewing window
with 1 x 50 and 1.7 y 2.1.
GRAPHING EXPLORATION
x
x
h
Figure 4–45
1500
0
24
0
Figure 4–46
——
—————
—
————
—— —
—
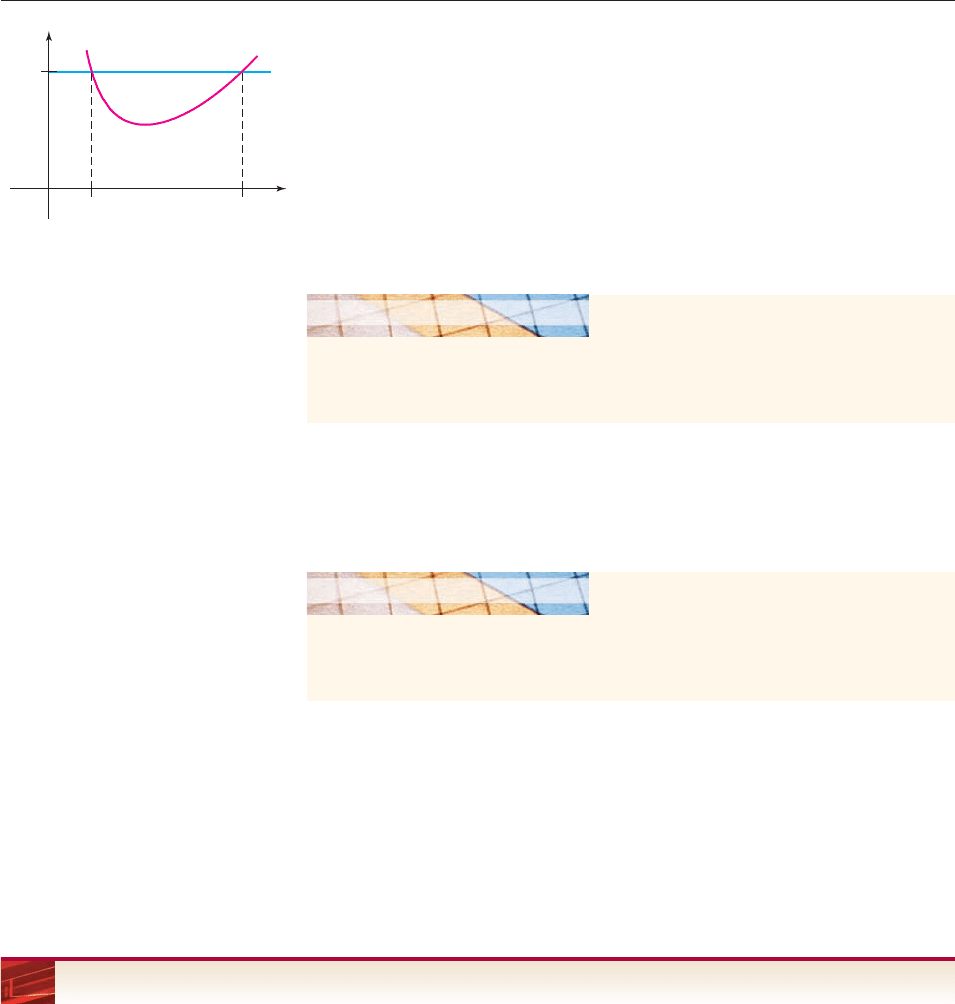
(x, y) on the graph, x is a possible side length for the base of the box, and y is
the corresponding surface area.
(a) The points on the graph corresponding to the requirement that no more than
1100 square inches of cardboard be used are those whose y-coordinates are
less than or equal to 1100. The x-coordinates of these points are the possible
side lengths. The x-coordinates of the points where the graph of S meets
the horizontal line y 1100 are the smallest and largest possible values for x,
as indicated in Figure 4–47.
300 CHAPTER 4 Polynomial and Rational Functions
y
1100
Smallest
x-coordinate
Largest
x-coordinate
x
Figure 4–47
Graph S(x) and y 1100 on the same screen. Use an intersection finder to show that
the possible side lengths that use no more than 1100 square inches of cardboard are
those with 3.73 x 21.36.
GRAPHING EXPLORATION
Show that the graph of S has a local minimum at the point (10.00, 600.00). Conse-
quently, the least possible amount of cardboard is 600 square inches and this occurs
when x 10.
GRAPHING EXPLORATION
(b) The least possible amount of cardboard corresponds to the point on the graph
of S(x) with the smallest y-coordinate.
(c) When x 10, h 1000/10
2
10. So the dimensions of the box using the
least amount of cardboard are 10 10 10. ■
EXERCISES 4.5
In Exercises 1–6, find the domain of the function. You may need
to use some of the techniques of Section 4.3
1. f (x)
3x
2
x
4
2. g(x)
2x
2
x
x
1
3
3. h(x)
x
x
2
2
4
9
4. i(x)
x
x
5
4
8
2
1
x
x
3
5. j(x)
6. k(x)
x
5
4
2
x
4
4
x
x
3
x
2
9x 9
In Exercises 7–10, find equations of graphs with the given
properties. Check your answer by graphing your function.
7. f has vertical asymptotes at x 3 and x 3, and a hori-
zontal asymptote at y 2
8. f has no vertical asymptotes, has a horizontal asymptote at
the x axis, and goes through the point (0,2)
9. f has four vertical asymptotes, a horizontal asymptote at
y 1, goes through the point (0,4) and is an even
function.
10. f has a vertical asymptote at x 2, and a hole at x 3.
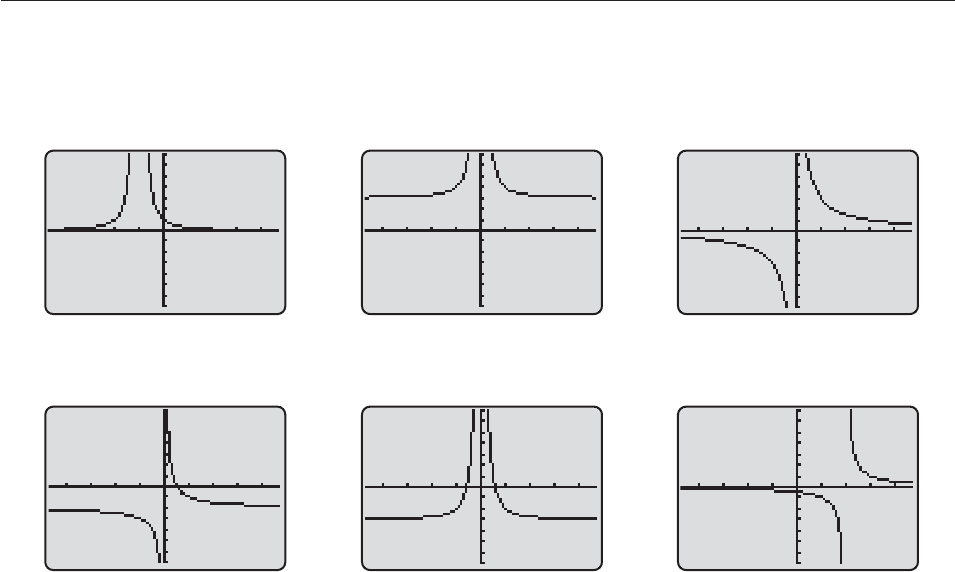
In Exercises 11–14, use the graphs in Example 1 and the
information in Section 3.4 to match the function with its
graph, which is one of those shown here.
A. B.
7
−7
−4.7 4.7
7
−7
−4.7 4.7
7
−7
−4.7 4.7
7
−7
−4.7 4.7
7
−7
−4.7 4.7
7
−7
−4.7 4.7
C.
D. E. F.
SECTION 4.5 Rational Functions 301
11. f (x)
x
1
2
12. g(x)
3
x
13. h(x)
(x
1
1)
2
14. f (x)
x
1
2
3
In Exercises 15–18, use algebra to determine the location of
the vertical asymptotes and holes in the graph of the function.
15. f (x)
16. g(x)
x
4
x
2
x
2
17. f (x)
x
x
2
2
8
7
x
x
2
2
18. g(x)
x
x
3
3
5
4
x
x
2
2
8
5
x
x
4
2
In Exercises 19–24, find the horizontal asymptote, if any, of the
graph of the given function. If there is a horizontal asymptote,
find a viewing window in which the ends of the graph are
within .1 of this asymptote.
19. f (x)
x
x
6
2
1
0
20. g(x)
21. a(x)
x
x
4
5
2
x
x
2
x
3
3x
5
2x
4
1
6x
5
8x
4
3x
2
2x 1
x
3
6x
2
11x 6
x
3
x
22. m(x)
x
2
x
2x
6
1
23. f (x)
24. r(x)
x
x
4
5
2
x
x
2
x
3
In Exercises 25–36, analyze the function algebraically. List its
vertical asymptotes, holes, y-intercept, and horizontal asymp-
tote, if any. Then sketch a complete graph of the function.
25. f(x)
x
1
2
26. f(x)
x
7
6
27. f(x)
x
2
x
1
28. f(x)
2x
2
x
3
29. f(x)
x
(x 2
x
)(x 3)
30. f(x)
(x 2
5
)
x
(
2
x 3)
31. f(x)
x
2
2
1
32. f(x)
(x 1)
5
2
(x 4)
33. f(x)
34. f(x)
x
3
x
2
2x
2
x
x
12
2
35. f(x)
36. f(x)
(x 1)(x 2)(x 3)
(4x 1)
2x
3
3x
2
3x 2
x
3
x
2
4x 4
(x
2
6x 5)(x 5)
(x 5)
3
(x 1)
2x
3
4x
2
2x 1
3x
3
4x
2
2x
In Exercises 37–42, find a viewing window, or windows, that
shows a complete graph of the function. Be alert for hidden
behavior, such as that in Example 6.
37. f(x)
38. g(x)
39. h(x)
x
2
3
x
2
x
2
x
6
6
x
40. f(x)
41. g(x)
42. h(x)
In Exercises 43–48, find and simplify the difference quotient of
the function. [See Sections 3.2 and 3.6]
43. f(x)
1
x
44. g(x)
3
2
x
45. f(x)
x
3
2
46. h(x)
x
1
2
47. g(x)
x
3
2
48. f(x)
n
m
x
2
49. (a) Use the difference quotient in Exercise 43 to determine
the average rate of change of f (x) 1/x as x changes
from 2 to 2.1, from 2 to 2.01, and from 2 to 2.001. Esti-
mate the instantaneous rate of change of f at x 2.
(b) Determine the average rate of change of f (x) 1/x as x
changes from 3 to 3.1, from 3 to 3.01, and from 3 to 3.001.
Estimate the instantaneous rate of change of f at x 3.
(c) How are the instantaneous rates of change of f at
x 2 and x 3 related to the values of the function
g(x) 1/x
2
at x 2 and x 3?
50. One way to limit current in a circuit is to add a “resistor.”
Resistance is measured in Ohms, and can never be negative.
If two resistors are wired “in series” the total resistance is
simply the sum R
1
R
2
.
It is more interesting if we wire them “in parallel.”
In that case we get: Total Resistance .
1
R
1
1
R
1
2
R
1
R
2
R
1
R
2
x
2
9
x
3
2x
2
23x 60
x 2
x
3
11x
2
x 11
x
3
x 1
x
4
2x
3
2x
2
x 1
x
4
2x
3
13x
2
10x
x 7
x
3
4x
2
5x
(x
2
4)(x
2
9)
302 CHAPTER 4 Polynomial and Rational Functions
Assume that two resistors are wired in parallel and that R
1
is
5 Ohms.
(a) Write the total resistance as a rational function of R
2
.
(b) If we allow R
2
to get larger and larger, the total resist-
ance approaches a value. Compute that value.
(c) Is the total resistance defined if R
2
0?
(d) What happens to the total resistance if R
2
gets closer
and closer to zero?
(e) Sketch a graph of total resistance vs. R
2
.
51. (a) When x 0, what rational function has the same graph as
f (x)
x
x
1
2
?
[Hint: Use the definition of absolute value on page 9.]
(b) When x 0, what rational function has the same graph as
f (x)
x
x
1
2
?
[See the hint for part (a).]
(c) Use parts (a) and (b) to explain why the graph of
f (x)
x
x
1
2
has two vertical asymptotes. What are they? Confirm your
answer by graphing the function.
52. Newton’s law of gravitation states that every object in the
universe attracts every other object, to some extent. If one
object has mass a and the other has mass b then the force
that they exert on each other is given by the equation
F G
a
d
b
2
, where d is the distance between the objects, and
G is a constant called, appropriately, the Gravitational
Constant. We can approximate G rather well by
G 6.673 10
11
. So if we put a 90 kilogram person about
2 meters from a 80 kilogram person, there would be a force of
(6.673 10
11
)
(90
2
)(
2
80)
1.201 10
7
Newtons between
them, or about .000000027 pounds.
(a) Use the force equation to determine what happens to the
force between two objects as they get farther and far-
ther apart.
(b) Use the force equation to determine what happens to the
force between two objects as they get closer and closer
together.
(c) The mass of the moon is approximately 7.36 10
22
kilograms. The mass of the Earth is approximately
5.97 10
24
kilograms. The distance from the moon to
the Earth ranges from 357,643 km to 406,395 km. Draw
a graph of the force that the Earth exerts on the moon
versus their distance apart.
53. It costs 2.5 cents per square inch to make the top and bottom
of the box in Example 7. The sides cost 1.5 cents per square
inch. What are the dimensions of the cheapest possible box?
54. A box with a square base and a volume of 1000 cubic inches
is to be constructed. The material for the top and bottom of
the box costs $3 per 100 square inches, and the material for
the sides costs $1.25 per 100 square inches.
(a) If x is the length of a side of the base, express the cost of
constructing the box as a function of x.
(b) If the side of the base must be at least 6 inches long, for
what value of x will the cost of the box be $7.50?
55. Our friend Joseph collects “action figures.” In 1980, his an-
nual action figure budget was $20, but it has gone up by $5
every year after that. The cost of action figures has risen as
well. In 1980, they cost an average of $2 per figure, but that
number has gone up by .25 every year after that.
(a) How many figures could Joseph buy in 1980?
(b) How many figures will he be able to buy in 2010?
(c) Write the number of figures he can buy in a given year
as a function of time. Let t 0 correspond to 1980.
(d) Graph the function you found in part (c). Use your
graph to check your answer to part (b).
(e) Will he ever be able to buy 18? If so, when? Will he
ever be able to buy 21? If so, when?
56. Pure alcohol is being added to 100 gallons of a coolant mix-
ture that is 40% alcohol.
(a) Find the rule of the concentration function c(x) that
expresses the percentage of alcohol in the resulting
mixture as a function of the number x of gallons of pure
alcohol that are added. [Hint: The final mixture con-
tains 100 x gallons (why?). So c(x) is the amount of
alcohol in the final mixture divided by the total amount
100 x. How much alcohol is in the original 100-gallon
mixture? How much is in the final mixture?]
(b) How many gallons of pure alcohol should be added to
produce a mixture that is at least 60% alcohol and no
more than 80% alcohol? Your answer will be a range of
values.
(c) Determine algebraically the exact amount of pure alco-
hol that must be added to produce a mixture that is 70%
alcohol.
57. A rectangular garden with an area of 200 square meters is to
be located next to a building and fenced on three sides, with
the building acting as a fence on the fourth side.
(a) If the side of the garden parallel to the building has
length x meters, express the amount of fencing needed
as a function of x.
(b) For what values of x will less than 60 meters of fencing
be needed?
(c) What value of x will result in the least possible amount
of fencing being used? What are the dimensions of the
garden in this case?
58. A certain company has fixed costs of $40,000 and variable
costs of $2.60 per unit.
(a) Let x be the number of units produced. Find the rule of
the average cost function. [The average cost is the cost
of the units divided by the number of units.]
(b) Graph the average cost function in a window with
0 x 100,000 and 0 y 20.
(c) Find the horizontal asymptote of the average cost func-
tion. Explain what the asymptote means in this situa-
tion. [How low can the average cost possibly be?]
SECTION 4.5 Rational Functions 303
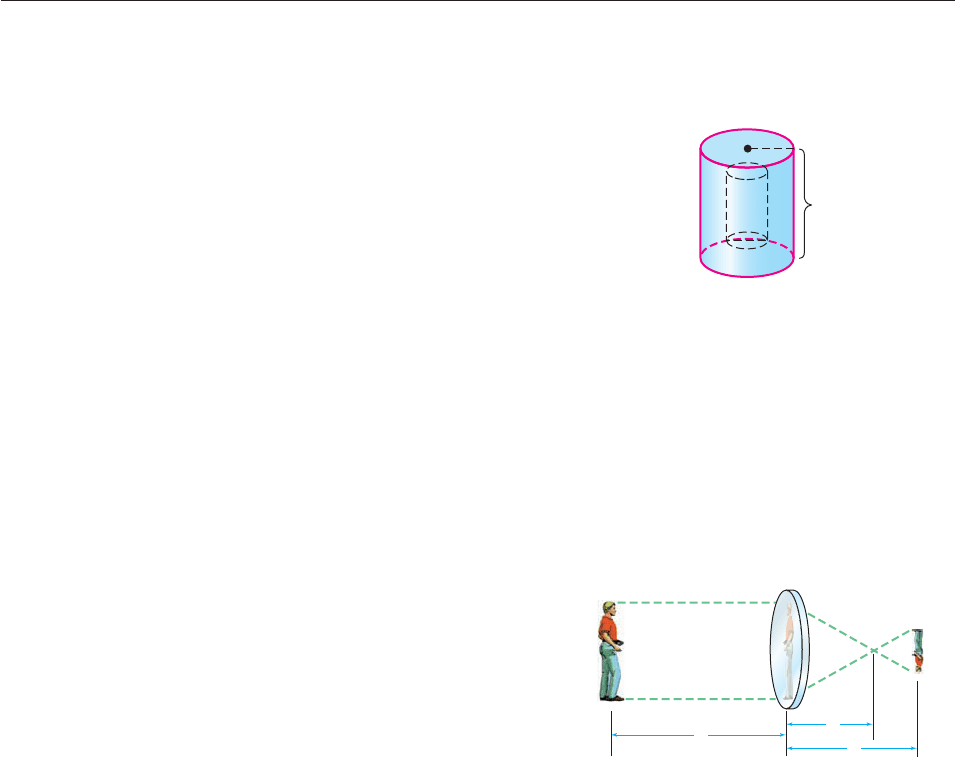
59. Radioactive waste is stored in a cylindrical tank; the exterior
has radius r and height h as shown in the figure. The sides, top,
and bottom of the tank are 1 foot thick, and the tank has a vol-
ume of 150 cubic feet (including top, bottom, and walls).
(a) Express the interior height h
1
(that is, the height of the
storage area) as a function of h.
(b) Express the interior height as a function of r.
(c) Express the volume of the interior as a function of r.
(d) Explain why r must be greater than 2.
(e) What should the dimensions of the tank be in order for
it to hold as much as possible?
60. The relationship between the fixed focal length F of a cam-
era, the distance u from the object being photographed to the
lens, and the distance v from the lens to the film is given by
F
1
1
u
1
v
.
(a) If the focal length is 50 millimeters, express v as a
function of u.
(b) What is the horizontal asymptote of the graph of the
function in part (a)?
(c) Graph the function in part (a) when
50 millimeters u 35,000 millimeters.
(d) When you focus the camera on an object, the distance
between the lens and the film is changed. If the distance
from the lens to the film changes by less than .1 mil-
limeter, the object will remain in focus. Explain why
you have more latitude in focusing on distant objects
than on very close ones.
61. The formula for the gravitational acceleration (in units of me-
ters per second squared) of an object relative to the earth is
g(r) ,
where r is the distance in meters above the earth’s surface.
(a) What is the gravitational acceleration at the earth’s
surface?
(b) Graph the function g(r) for r 0.
(c) Can you ever escape the pull of gravity? [Does the
graph have any r-intercepts?]
3.987 10
14
(6.378 10
6
r)
2
u
F
v
h
r
304 CHAPTER 4 Polynomial and Rational Functions
■ Find the graph of a rational function whose numerator has larger
degree than its denominator.
We now take a closer look at the graphs of rational functions in which the degree
of the numerator is larger than the degree of the denominator. We have seen that
such graphs do not have horizontal asymptotes. It turns out we can use polynomial
division to find out what these graphs look like when x is very large.
EXAMPLE 1
Describe the behavior of f (x)
x
3
x
2
3
x
2
2x
x
1
1
when x is very large.
SOLUTION We divide the numerator of f(x) by its denominator:
x 1
x
2
2x 1 x
3
3x
2
x 1
x
3
2x
2
x
x
2
2x 1
x
2
2x 1
2.
By the Division Algorithm,
x
3
3x
2
x 1 (x
2
2x 1)(x 1) 2.
Dividing both sides by x
2
2x 1, we have
x
3
x
2
3
x
2
2x
x
1
1
f (x) (x 1)
x
2
2
2
x 1
.
Now when x is very large in absolute value, so is x
2
2x 1. Hence,
2/(x
2
2x 1) is very close to 0 by the Big-Little Principle, and f (x) is very
close to (x 1) 0. Therefore, as x gets larger in absolute value, the graph of f (x)
gets closer and closer to the line y x 1. An asymptote such as this (that is, a
nonvertical and non horizontal straight line) is called an oblique asymptote.
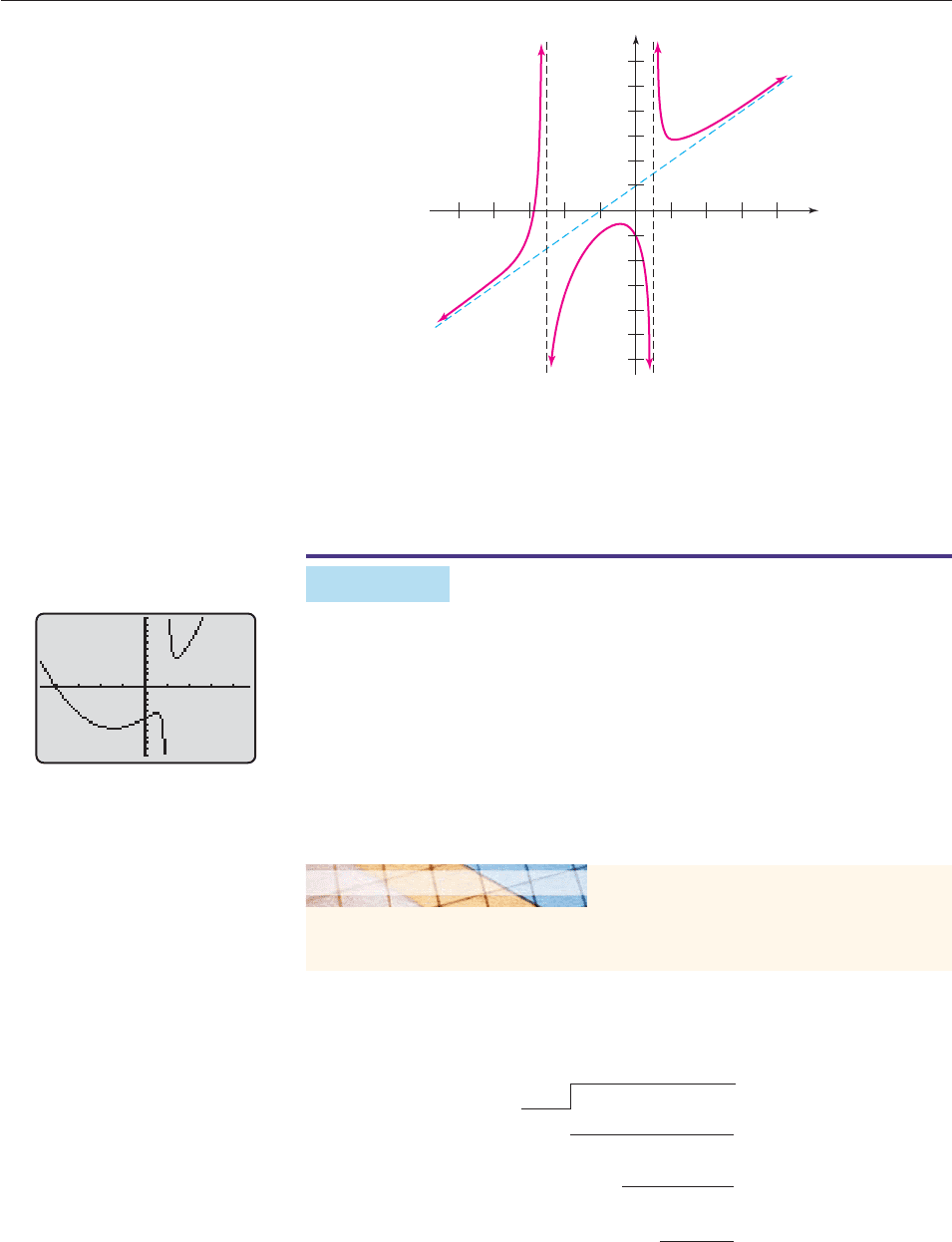
The graph of f(x) is shown in Figure 4–48. Notice that there two vertical
asymptotes, corresponding to the roots of its denominator, and that as x gets very
large, it gets closer and closer to the graph of y x 1, as predicted. Except near
the vertical asymptotes of f (x), the two graphs are virtually identical.
(x
2
2x 1)(x 1) 2
x
2
2x 1
4.5.A SPECIAL TOPICS Other Rational Functions
Section Objective
——
Verify the last sentence above as follows. Using the viewing window with
20 x 20 and 20 y 20, graph both f(x) and y x 1 on the same screen.
■
GRAPHING EXPLORATION
The long division process shown in Example 1 works for a general rational func-
tion. As x gets larger in absolute value, the graph of a rational function gets closer and
closer to the quotient obtained when its numerator is divided by its denominator.
EXAMPLE 2
Graph
g(x) .
SOLUTION We first note that there is a vertical asymptote at x 1 (root of the
denominator, but not the numerator). The y-intercept is at g(0) 5. By carefully
choosing a viewing window that accurately portrays the behavior of g(x) near its
vertical asymptote, we obtain Figure 4–49.
x
3
2x
2
7x 5
x 1
SPECIAL TOPICS 4.5.A Other Rational Functions 305
x
y
1
−11
Verify that the x-intercept near x 4 is the only one by showing graphically that
the numerator of g(x) has exactly one real root.
GRAPHING EXPLORATION
Figure 4–48
11
4.7
−4.7
−11
Figure 4–49
To confirm that Figure 4–49 is a complete graph, we find its asymptote when x
is large. Divide the numerator by the denominator.
x
2
3x 4
x 1 x
3
2x
2
7x 5
x
3
x
2
3x
2
7x 5
3x
2
3x
4x 5
4x 4
1
