Hungerford T.W., Shaw D.J. Contemporary Precalculus: A Graphing Approach
Подождите немного. Документ загружается.

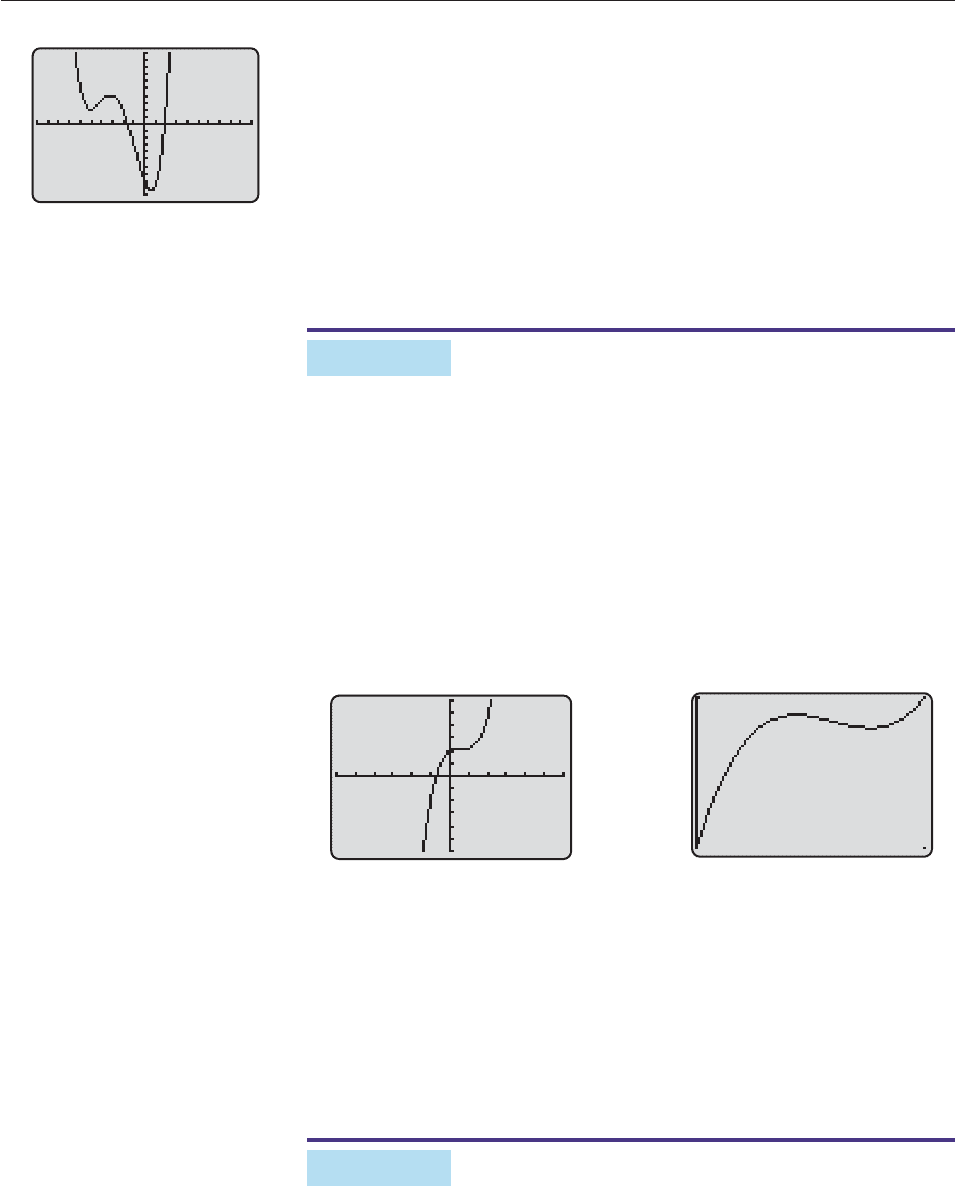
SOLUTION Since f (0) 80, the standard viewing window probably won’t
show a complete graph, so we try the window with
10 x 10 and 100 y 100
and obtain Figure 4–21. The three peaks and valleys shown here are the only ones
because a fourth-degree polynomial graph has at most three local extrema. There
cannot be more x-intercepts than the two shown here because if the graph turned
toward the x-axis farther out, there would be an additional peak, which is impos-
sible. Finally, the outer ends of the graph resemble the graph of x
4
, the highest-
degree term (see the chart on page 270). Hence, Figure 4–21 includes all the
important features of the graph and is therefore complete. ■
EXAMPLE 5
Find a complete graph of f (x) x
3
1.8x
2
x 2.
SOLUTION We first try the standard window (Figure 4 –22). The graph is sim-
ilar to the graph of the leading term y x
3
but does not appear to have any local
extrema. However, if you use the trace feature on the flat portion of the graph
to the right of the x-axis, you see that the y-coordinates increase, then decrease,
then increase (try it!). Zooming in on the portion of the graph between 0 and 1
(Figure 4–22), we see that the graph actually has a tiny peak and valley (the maxi-
mum possible number of local extrema for a cubic). So Figures 4–22 and 4–23
together provide a complete graph of f. ■
276 CHAPTER 4 Polynomial and Rational Functions
100
10
−10
−100
Figure 4–21
6
6
−6
−6
2.2
1
0
2
Figure 4–22
Figure 4–23
The following fact is proved in Exercise 59.
No nonconstant polynomial graph contains any horizontal line segments.
However, a calculator may erroneously show horizontal segments, as in Fig-
ure 4–22. So always investigate such segments, by using trace or zoom-in, to
determine any hidden behavior, such as that in Example 5.
EXAMPLE 6
The graph of f (x) .01x
5
x
4
x
3
6x
2
5x 4 in the standard window is
shown in Figure 4–24. Explain why this is not a complete graph and find a com-
plete graph of f.
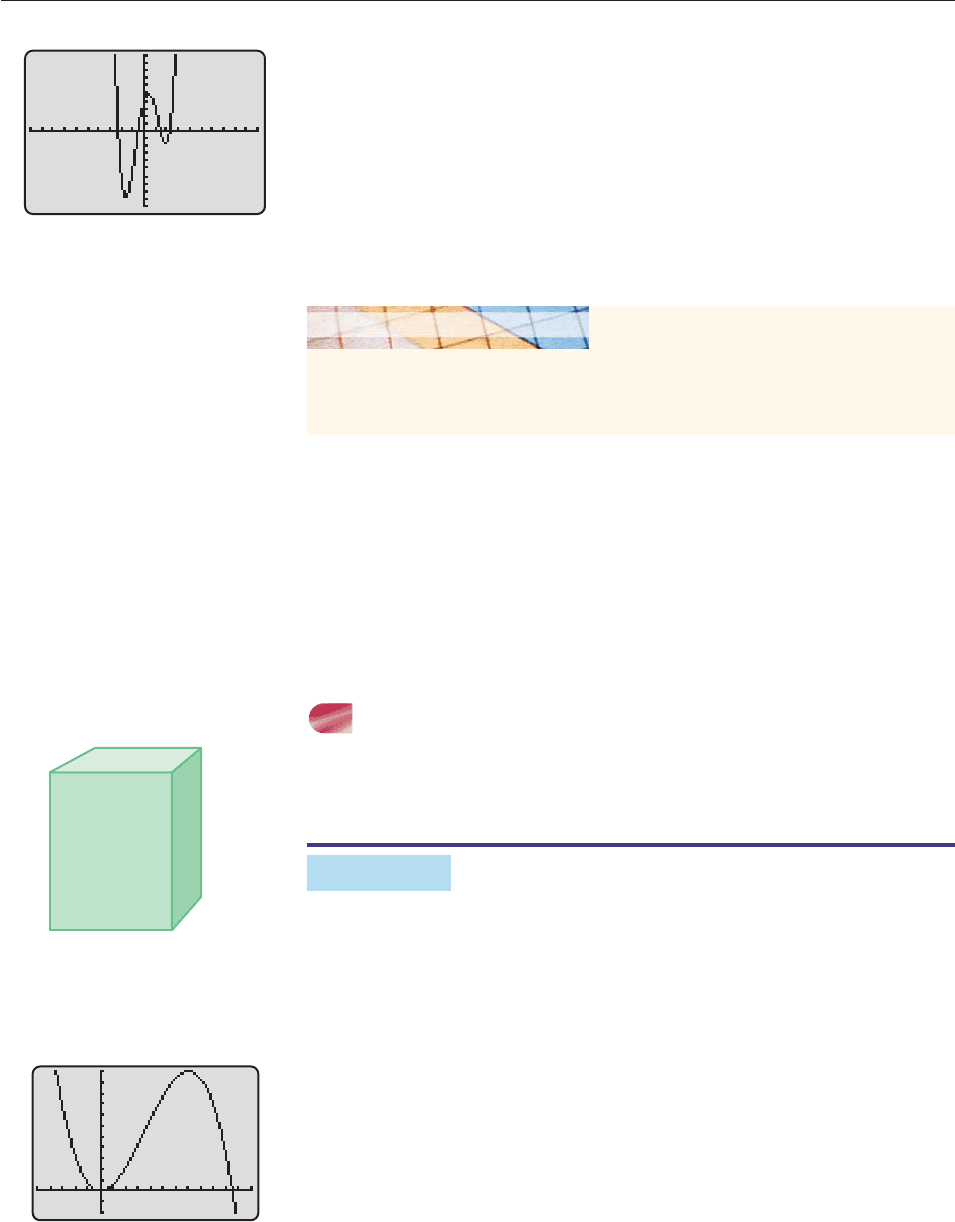
SOLUTION When x is large, the graph of f must resemble the graph of
y .01x
5
, whose left end goes downward (see the chart on page 270). Since
Figure 4–24 does not show this, it is not a complete graph. To have the same
shape as the graph of y .01x
5
, the graph of f must turn downward and cross
the x-axis somewhere to the left of the origin. Figure 4 –24 shows three local
extrema. Even without graphing, we can see that there must be one more peak
(where the graph turns downward on the left), making a total of four local extrema
(the most a fifth-degree polynomial can have), and another x-intercept, for a
total of five. When these additional features are shown, we will have a
complete graph.
SECTION 4.4 Graphs of Polynomial Functions 277
10
10
−10
−10
Figure 4–24
Find a viewing window that includes the local maximum and x-intercept not shown
in Figure 4–24. When you do, the scale will be such that the local extrema and
x-intercepts shown in Figure 4–24 will no longer be visible.
GRAPHING EXPLORATION
Consequently, a complete graph of f(x) requires several viewing windows in order
to see all the important features. ■
The graphs obtained in Examples 4–6 were known to be complete because in
each case, they included the maximum possible number of local extrema. In many
cases, however, a graph may not have the largest possible number of peaks and
valleys. In such cases, use any available information and try several viewing win-
dows to obtain the most likely complete graph.
APPLICATIONS
The solution of many applied problems reduces to finding a local extremum of a
polynomial function.
EXAMPLE 7
A rectangular box with a square base (Figure 4–25) is to be mailed. The sum of
the height of the box and the perimeter of the base is to be 84 inches, the maxi-
mum allowable under postal regulations. What are the dimensions of the box with
largest possible volume that meets these conditions?
SOLUTION If the length of one side of the base is x, then the perimeter of the
base (the sum of the length of its four sides) is 4x. If the height of the box is d, then
4x d 84, so d 84 4x, and hence, the volume is
V x
x
d x
x
(84 4x) 84x
2
4x
3
.
The graph of the polynomial function V(x) 84x
2
4x
3
in Figure 4–26 is com-
plete (why?). However, the only relevant part of the graph in this situation is the
portion with x and V(x) positive (because x is a length and V(x) is a volume). The
graph of V(x) has a local maximum between 10 and 20, and this local maximum
value is the largest possible volume for the box.
x
x
d
Figure 4–25
5500
24
−10
−1000
Figure 4–26
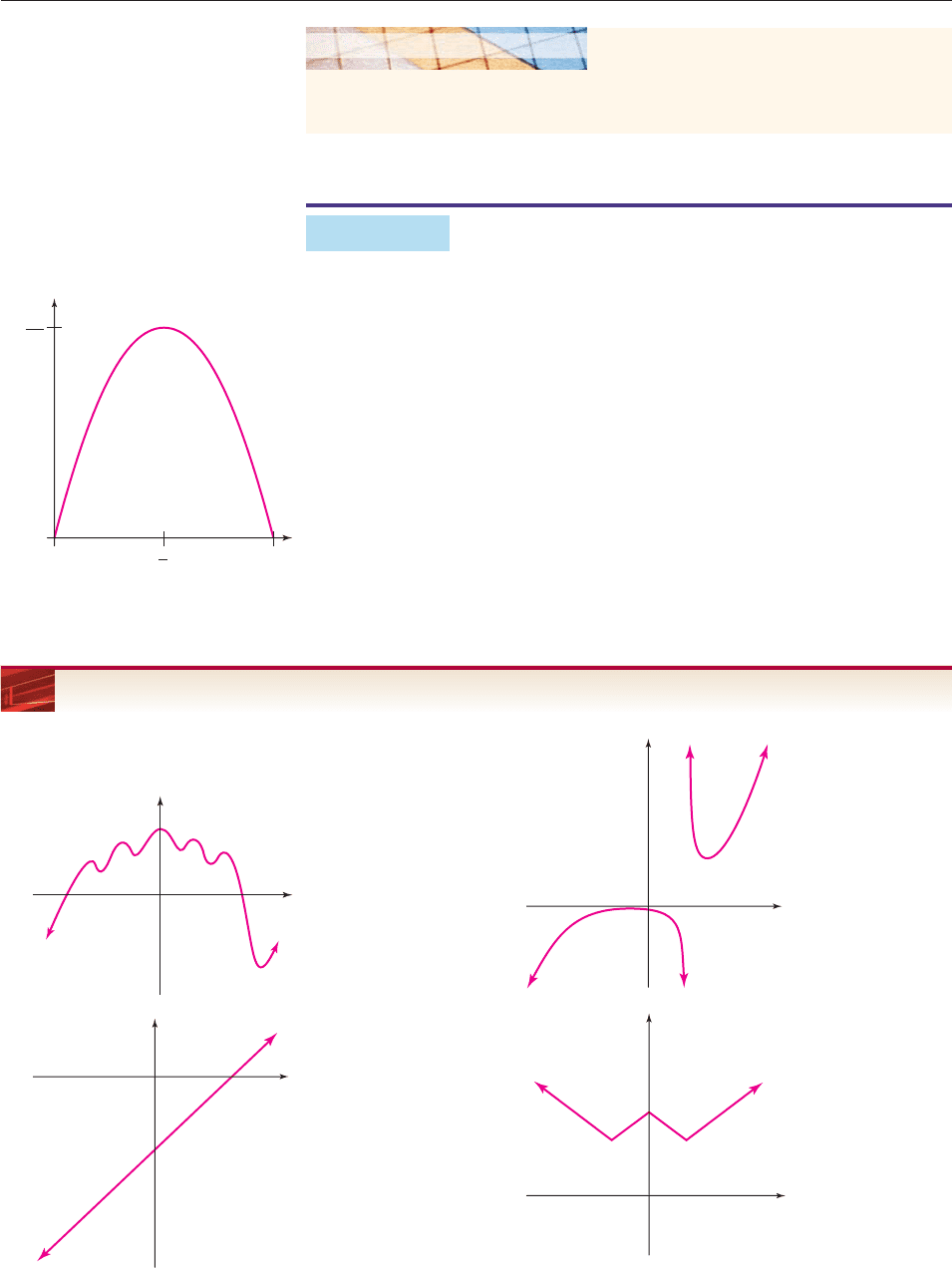
EXAMPLE 8
Assume we let some box-elder bugs loose in a neighborhood, and want to model
their population growth. The “carrying capacity” of an environment is the number
of box-elder bugs that it can support. According to one model, the rate at which a
population grows is proportional to its size, and to the difference between that size
and the environment’s carrying capacity. We can write this model as an equation:
R kP(C P)
where R is the rate of growth, P is the population, C is the carrying capacity, and
k is a constant of proportionality. If we multiply the equation out we get a poly-
nomial, where P is our variable:
R (k)P
2
(kC)P
The graph of this polynomial is given in Figure 4–27. If we wish to graph this equa-
tion on a calculator, we would have to choose sample values for C and k. ■
278 CHAPTER 4 Polynomial and Rational Functions
Use a maximum finder to find the x-value at which the local maximum occurs. State
the dimensions of the box in this case.
■
GRAPHING EXPLORATION
0
0
Rate of growth
C
kC
2
4
C
2
p
y
Figure 4–27
EXERCISES 4.4
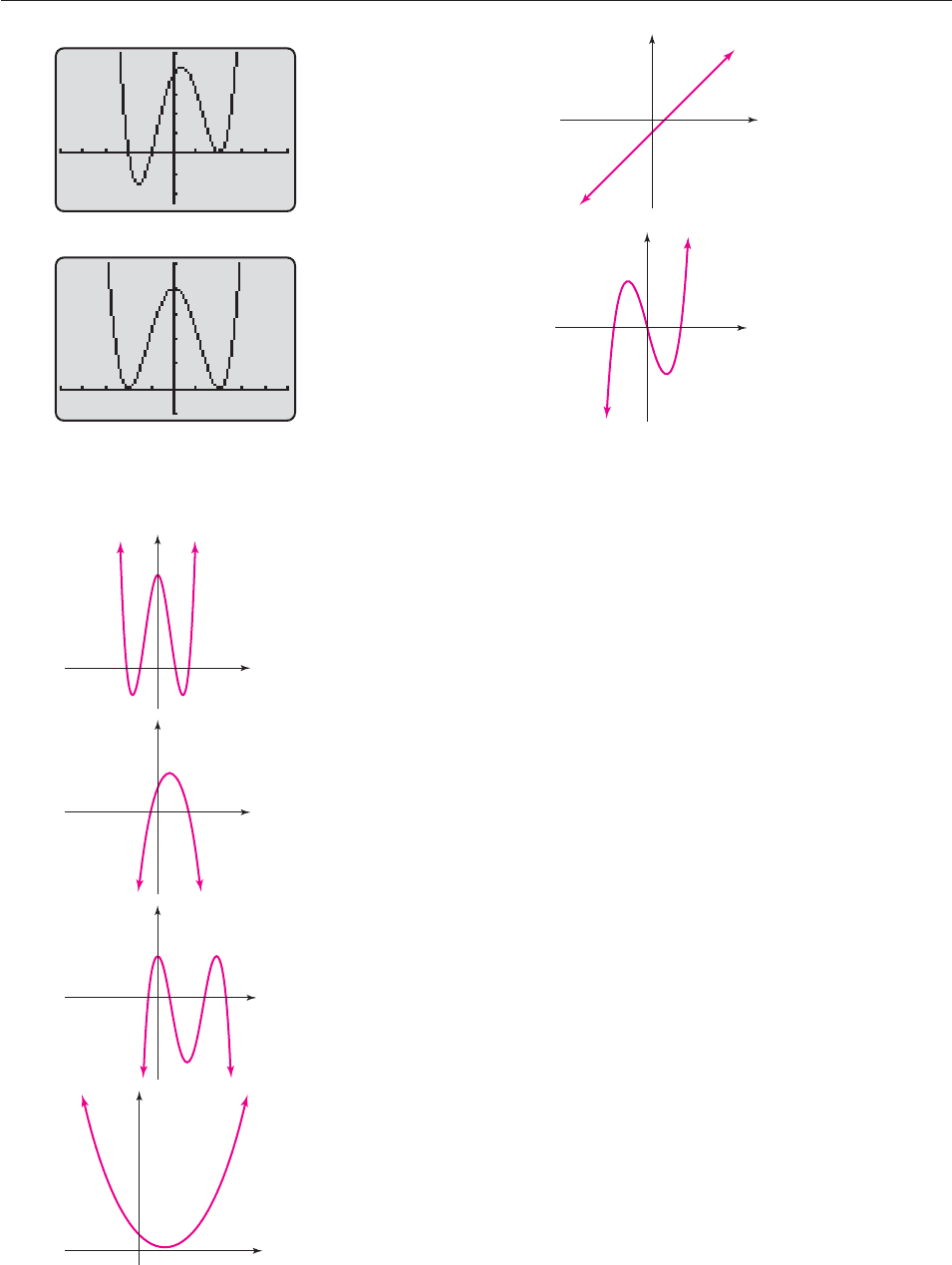
In Exercises 1–6, decide whether the given graph could possi-
bly be the graph of a polynomial function.
1.
2.
x
y
x
y
3.
4.
x
y
x
y
SECTION 4.4 Graphs of Polynomial Functions 279
5.
6.
In Exercises 7–12, determine whether the given graph could
possibly be the graph of a polynomial function of degree 3, of
degree 4, or of degree 5.
7.
8.
9.
x
y
x
y
x
y
x
y
x
y
10.
11.
12.
In Exercises 13 and 14, find a viewing window in which the
graph of the given polynomial function f appears to have the
same general shape as the graph of its leading term.
13. f (x) x
4
6x
3
9x
2
3
14. f (x) x
3
5x
2
4x 2
In Exercises 15–18, a complete graph of a polynomial function
is shown. List each root of the polynomial and state whether its
multiplicity is even or odd.
15.
16.
4
5
−5
−14
10
5
−5
−6
x
y
x
y
x
y
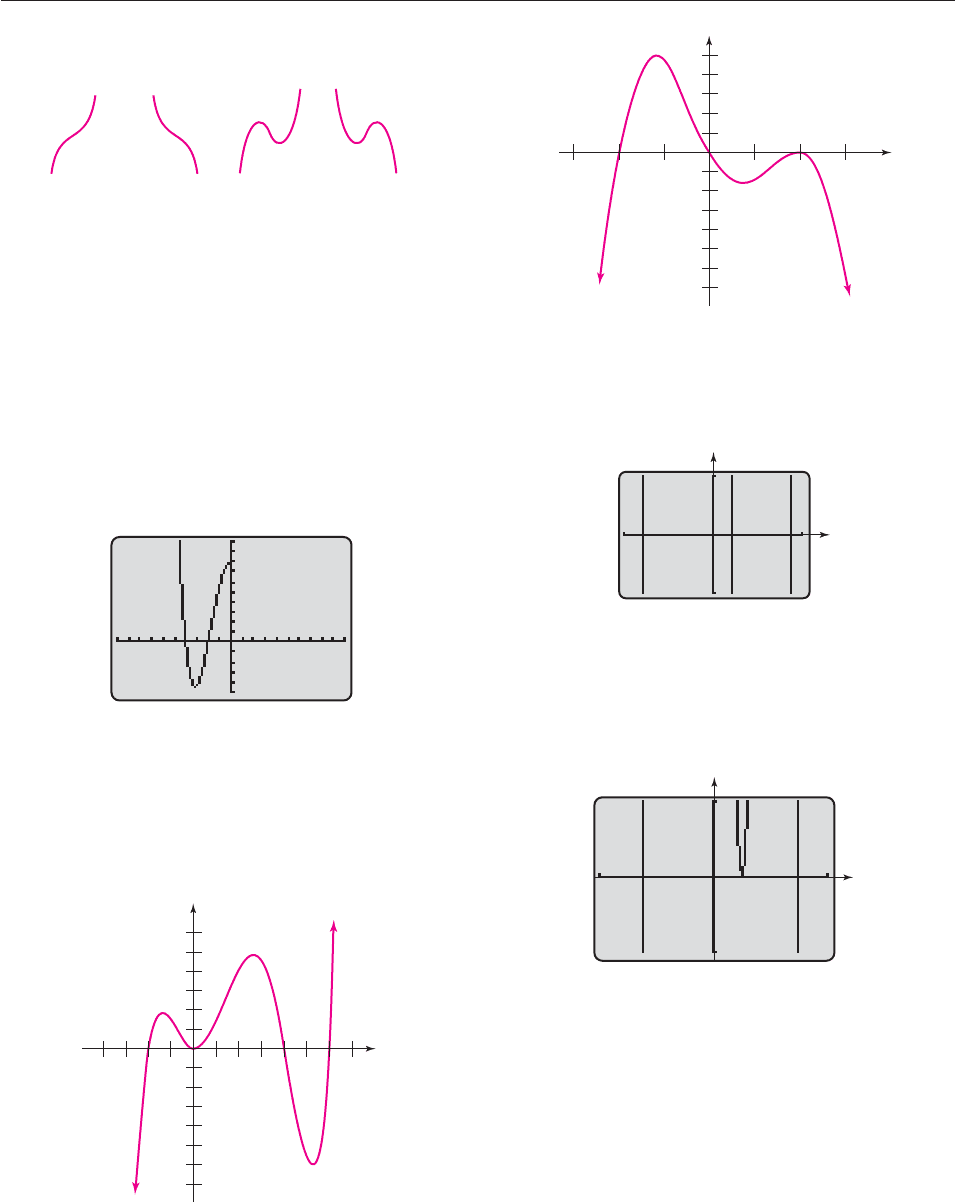
17.
18.
In Exercises 19–24, use your knowledge of polynomial graphs,
not a calculator, to match the given function with its graph,
which is one of (a)–(f).
(a)
(b)
(c)
(d)
x
y
x
y
x
y
x
y
20
5
−5
−4
10
5
−5
−5
280 CHAPTER 4 Polynomial and Rational Functions
(e)
(f)
19. f(x) 2x 3 20. g(x) x
2
4x 7
21. g(x) x
3
4x 22. f(x) x
4
5x
2
4
23. f(x) x
4
6x
3
9x
2
2
24. g(x) 2x
2
3x 1
In Exercises 25–28, graph the function in the standard viewing
window and explain why that graph cannot possibly be com-
plete.
25. f(x) .01x
3
.2x
2
.4x 7
26. g(x) .01x
4
.1x
3
.8x
2
.7x 9
27. h(x) .005x
4
x
2
5
28. f(x) .001x
5
.01x
4
.2x
3
x
2
x 5
In Exercises 29–32 find a single viewing window that shows a
complete graph of the function.
29. f(x) x
3
8x
2
20x 15
30. f(x) 10x
3
12x
2
2x
31. f(x) 10x
4
80x
3
239x
2
316x 155
32. f(x) 10x
4
80x
3
241x
2
324x 163
In Exercises 33–36, find a complete graph of the function and
list the viewing window(s) that show this graph. (It may not be
possible to obtain a complete graph in a single window.)
33. f(x) .1x
5
3x
4
4x
3
11x
2
3x 5
34. f(x) x
4
48x
3
101x
2
49x 50
35. f(x) .03x
3
1.5 x
2
200x
36. f(x) .3x
5
2x
4
7x
3
2x
2
37. (a) Explain why the graph of a cubic polynomial function
has either two local extrema or none at all. [Hint: If it
had only one, what would the graph look like when x
is very large?]
x
y
x
y
(b) Explain why the general shape of the graph of a cubic
polynomial function must be one of the following:
(a) (b) (c) (d)
38. The figure shows an incomplete graph of a fourth-degree
even polynomial function f. (Even functions were defined
in Special Topics 3.4.A.)
(a) Find the roots of f.
(b) Draw a complete graph of f.
(c) Explain why
f(x) k(x a)(x b)(x c)(x d ),
where a, b, c, d are the roots of f.
(d) Experiment with your calculator to find the value of k
that produces the graph in the figure.
(e) List the approximate intervals on which f is increasing
and those on which it is decreasing.
39. A complete graph of a polynomial function g is shown
below.
(a) Is the degree of g(x) even or odd?
(b) Is the leading coefficient of g(x) positive or negative?
(c) What are the real roots of g(x)?
(d) What is the smallest possible degree of g(x)?
40. Do Exercise 39 for the polynomial function g whose com-
plete graph is shown here.
x
y
−4 −22
−5
5
10
15
−10
−15
46
20
10
−10
−10
SECTION 4.4 Graphs of Polynomial Functions 281
41. f is a third degree polynomial function whose leading coef-
ficient is negative. Gordon graphs the function on his calcu-
lator, without being careful about choosing a window, and
gets the plot shown below. Which of the patterns shown in
Exercise 37 does this graph have?
42. f is a fourth degree polynomial function. Madison graphs
the function on her calculator, without being careful about
choosing a window, and gets the plot shown below. Sketch
the general shape of the graph and state whether the leading
coefficient is positive or negative.
In Exercises 43–48, sketch a complete graph of the function.
Label each x-intercept and the coordinates of each local
extremum; find intercepts and coordinates exactly when
possible and otherwise approximate them.
43. f(x) x
3
3x
2
2
44. f(x) .25x
4
2x
3
4x
2
45. f (x) x
4
9x
3
30x
2
44x 24
46. f(x) 3x
3
18.5x
2
4.5x 45
47. f (x) x
5
3x
3
x
48. f (x) x
6
3x
3
9
4
x
y
y
x
x
y
−2−3 −11
−4
4
8
−8
−12
23

49. The sales f (x) of a certain product (in dollars) are related to
the amount x (in thousands of dollars) spent on advertising by
f (x) 3x
3
135x
2
3600x 12,000
(0 x 40).
(a) Graph f in the window with 0 x 40 and
0 y 180,000 and verify that f is concave upward
near the origin and concave downward near x 40.
(b) Compute the average rate of change of f (x) from
x 0 to x 15 and from x 15 to x 40. What do
these numbers tell you about the rate at which sales are
increasing in each interval?
(c) This function has an inflection point at x 15 (a fact
you might want to verify if your calculator can find in-
flection points). Use the results of part (b) to explain
why the inflection point is sometimes called the point
of diminishing returns.
50. The profits (in thousands of dollars) from producing x hun-
dred thousand tungsten darts are given by
g(x) x
3
27x
2
20x 60 (0 x 20).
(a) Graph g in a window with 0 x 20. If you have an
appropriate calculator, verify that there is a point of
inflection when x 9.
(b) Verify that the point of inflection is the point of dimin-
ishing returns (see Exercise 49) by computing the average
rate of change of profit from x 0 to x 9 and from
x 9 to x 20.
51. When there are 22 apple trees per acre, the average yield
has been found to be 500 apples per tree. For each addi-
tional tree planted per acre, the yield per tree decreases by
15 apples per tree. How many additional trees per acre
should be planted to maximize the yield?
52. Name tags can be sold for $29 per thousand. The cost of
manufacturing x thousand tags is .001x
3
.06x
2
1.5x
dollars. Assuming that all tags manufactured are sold,
(a) What number of tags should be made to guarantee a
maximum profit? What will that profit be?
(b) What is the largest number of tags that can be made
without losing money?
53. The top of a 12-ounce can of soda pop is three times thicker
than the sides and bottom (so that the flip-top opener will
work properly), and the can has a volume of 355 cubic cen-
timeters. What should the radius and height of the can be in
order to use the least possible amount of metal? [Assume
that the entire can is made from a single sheet of metal, with
three layers being used for the top. Example 4 in Section 2.4
may be helpful.]
54. An open-top reinforced box is to be made from a 12-by-
36-inch piece of cardboard as in Exercise 45 of Sec-
tion 4.3. What size squares should be cut from the corners in
order to have a box with maximum volume?
In calculus, you will learn that many complicated functions can
be approximated by polynomials. For Exercises 55–58, use a
282 CHAPTER 4 Polynomial and Rational Functions
calculator to graph the function and the polynomial on the
same axes in the given window, and determine where the poly-
nomial is a good approximation.*
55. f (x) sin(x), p(x)
50
1
40
x
7
1
1
20
x
5
1
6
x
3
x,
6 x 6, 4 y 4
56. f (x)
1
1
x
, p(x) x
7
x
6
x
5
x
4
x
3
x
2
x 1,
3 x 3, 6 y 6
57. (a) f (x) e
x
, p(x)
50
1
40
x
7
7
1
20
x
6
1
1
20
x
5
2
1
4
x
4
1
6
x
3
1
2
x
2
x 1, 6 x 6, 3 y 10
(b) f (x) e
x
, p(x)
50
1
40
x
7
7
1
20
x
6
1
1
20
x
5
2
1
4
x
4
1
6
x
3
1
2
x
2
x 1, 6 x 6, 50 y 400
[Hint: On some calculators, the “e
x
” key is labelled
“exp(x).”]
58. f (x) tan(x), p(x)
3
1
1
7
5
x
7
1
2
5
x
5
1
3
x
3
x, 3 x 3,
10 y 10
THINKERS
59. (a) Graph g(x) .01x
3
.06x
2
.12x 3.92 in the view-
ing window with 3 x 3 and 0 y 6 and verify
that the graph appears to coincide with the horizontal
line y 4 between x 1 and x 3. In other words, it
appears that every x with 1 x 3 is a solution of the
equation
.01x
3
.06x
2
.12x 3.92 4.
Explain why this is impossible. Conclude that the
actual graph is not horizontal between x 1 and
x 3.
(b) Use the trace feature to verify that the graph is actually
rising from left to right between x 1 and x 3. Find
a viewing window that shows this.
(c) Show that it is not possible for the graph of a polyno-
mial f (x) to contain a horizontal segment. [Hint: A hor-
izontal line segment is part of the horizontal line
y k for some constant k. Adapt the argument in part
(a), which is the case k 4.]
60. (a) Let f (x) be a polynomial of odd degree. Explain why
f (x) must have at least one real root. [Hint: Why must
the graph of f cross the x-axis, and what does this mean?]
(b) Let g(x) be a polynomial of even degree, with a nega-
tive leading coefficient and a positive constant term.
Explain why g(x) must have at least one positive and at
least one negative root.
*You don’t need to know what the SIN and e
x
keys mean to do this
exercise.

61. The graph of
f (x) (x 18)(x
2
20)(x 2)
2
(x 10)
has x-intercepts at each of its roots, that is, at x 18,
204.472, 2, and 10. It is also true that f (x) has a
relative minimum at x 2.
(a) Draw the x-axis and mark the roots of f (x). Then use
the fact that f (x) has degree 6 (why?) to sketch the
general shape of the graph (as was done for cubics in
Exercise 37).
(b) Now graph f (x) in the standard viewing window. Does
the graph resemble your sketch? Does it even show all
the x-intercepts between 10 and 10?
SPECIAL TOPICS 4.4.A Polynomial Models 283
(c) Graph f (x) in the viewing window with 19 x 11
and 10 y 10. Does this window include all the
x-intercepts as it should?
(d) List viewing windows that give a complete graph of f (x).
62. (a) Graph f (x) x
3
4x in the viewing window with
3 x 3 and 5 y 5.
(b) Graph the difference quotient of f (x) (with h .01) on
the same screen.
(c) Find the x-coordinates of the relative extrema of f (x).
How do these numbers compare with the x-intercepts of
the difference quotient?
(d) Repeat this problem with the function f(x) x
4
x
2
.
4.4.A SPECIAL TOPICS Polynomial Models*
■ Use regression to find polynomial models to fit real-life data.
In section 2.5 we started with a set of data points, and we found the best linear
model for those points. Our method was to use the calculator to compute the “least
squares regression line,” the line that minimized the sum of the squares of the
error terms. When the scatter plot of the data points looks more like a higher-
degree polynomial graph, we use a similar procedure to find a polynomial model
for the points. Most calculators have regression procedures that allow us to con-
struct quadratic, cubic and quartic (fourth-degree) models.
EXAMPLE 1
The table shows the population of San Francisco in selected years.
†
Section Objective
Year 1950 1960 1970 1980 1990 2000
Population 775,357 740,316 715,674 678,974 723,959 776,733
(a) Find a polynomial model for this data.
(b) Use the model to estimate the population of San Francisco in 1995 and 2005.
SOLUTION
(a) Let x 0 correspond to 1950 and plot the data points, as in Figure 4–28 on
the next page. We use quartic regression to obtain the following function:
f (x) .1072x
4
13.2x
3
387.24x
2
168.65x 774,231.
‡
*Section 2.5 is a prerequisite for this optional section. This material will be used in the optional
Section 5.5 and in clearly identified exercises but not elsewhere.
†
U.S. Census Bureau.
‡
Here and later, coefficients are rounded for convenient reading, but the full coefficients are used to
produce the graphs and estimates.
TECHNOLOGY TIP
The quadratic, cubic, and quartic re-
gression commands are in the same
menu as the linear regression com-
mand and are labeled as follows:
TI-84+/89: QuadReg, CubicReg,
QuartReg
TI-86: P2Reg, P3Reg, P4Reg.
Casio 9850: x2, x3, x 4,
HP-39gs: quadrati
c, cubic
Quartic regression is not available on
HP-39gs.
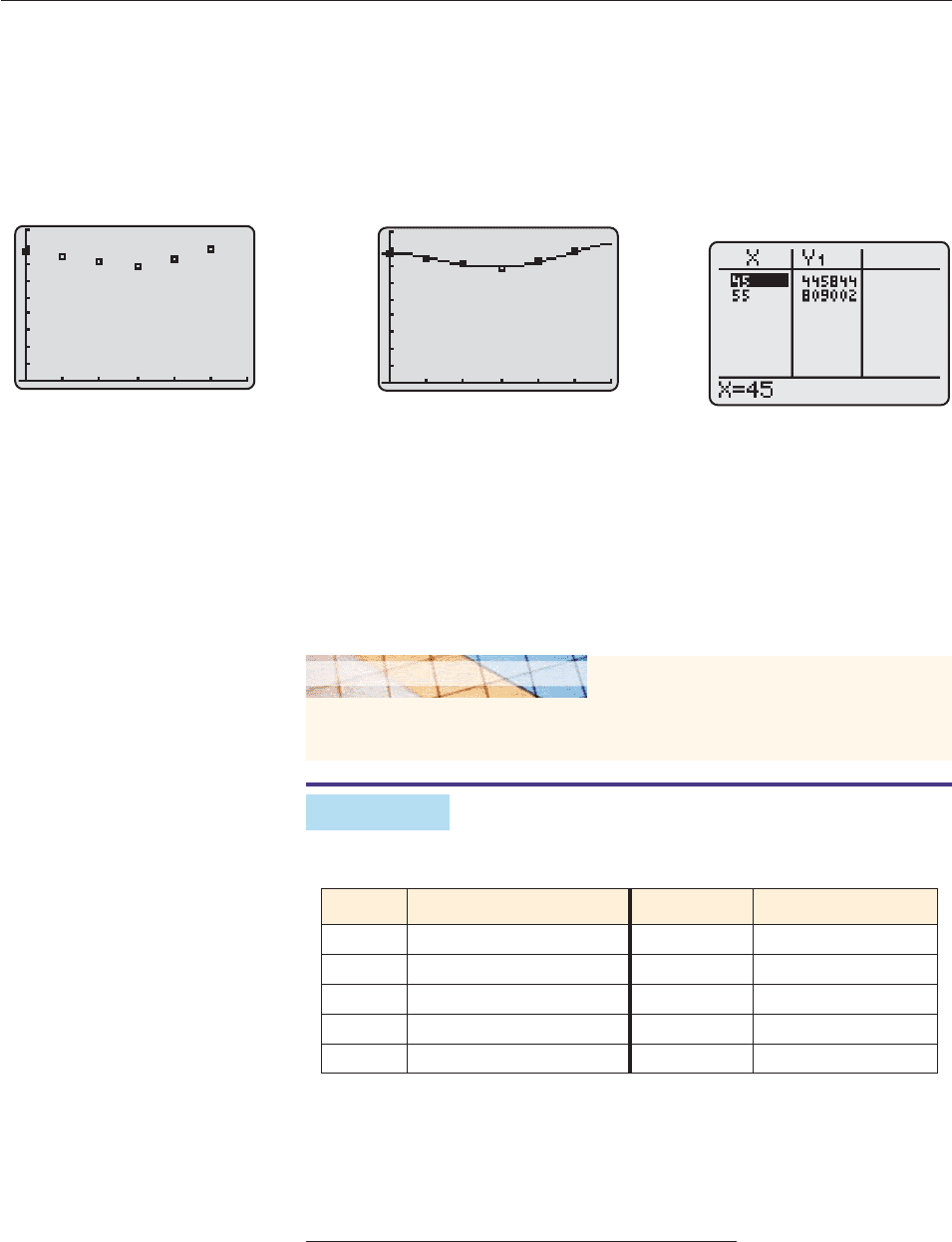
900,000
60
0
0
Figure 4–28
(The procedure is the same as for linear regression; see Example 3 on
page 123 and the Technology Tip in the margin of preceding page. The graph
of f in Figure 4–29 appears to fit the data well.
(b) To estimate the population in 1995 and 2005, we evaluate f at x 45 and
x 55, as shown in Figure 4–30. According to this model, the 1995 popula-
tion was about 745,844 and the 2005 population is about 809,002. ■
284 CHAPTER 4 Polynomial and Rational Functions
900,000
60
0
0
Figure 4–30
Figure 4–29
The actual population of San Francisco in 1995 was 730,628 and in 2005 was
739,426. Our estimate for 1995 in Example 1 was more accurate than the estimate
for 2005. This is because, if we don’t know a lot about a data set, it tends to be
safer to interpolate (use a model to fill in data between points) than to extrapolate
(use a model to predict data outside the data points). As we shall see later, popu-
lation data tends to lend itself best to exponential models, so our polynomial
model is not going to give very accurate extrapolations.
Use your minimum finder and the population function in Example 1 to estimate the
year since 1950 when the population of San Francisco was smallest.
GRAPHING EXPLORATION
EXAMPLE 2
The table below gives the average price of gasoline during various years*:
Year Gas Price ($/gal) Year Gas Price ($/gal)
1970 0.357 1990 1.127
1974 0.524 1994 1.075
1978 0.630 1998 1.030
1982 1.259 2002 1.341
1986 0.890 2006 2.594
Find a suitable polynomial model for this data.
SOLUTION Letting x 0 correspond to 1970 and plotting the data points we
obtain the scatter plot in Figure 4–31. The points are not in a straight line but
could be part of a polynomial graph of higher degree.
*From Bureau of Labor and Statistics. 2006 data averaged through part of the year.
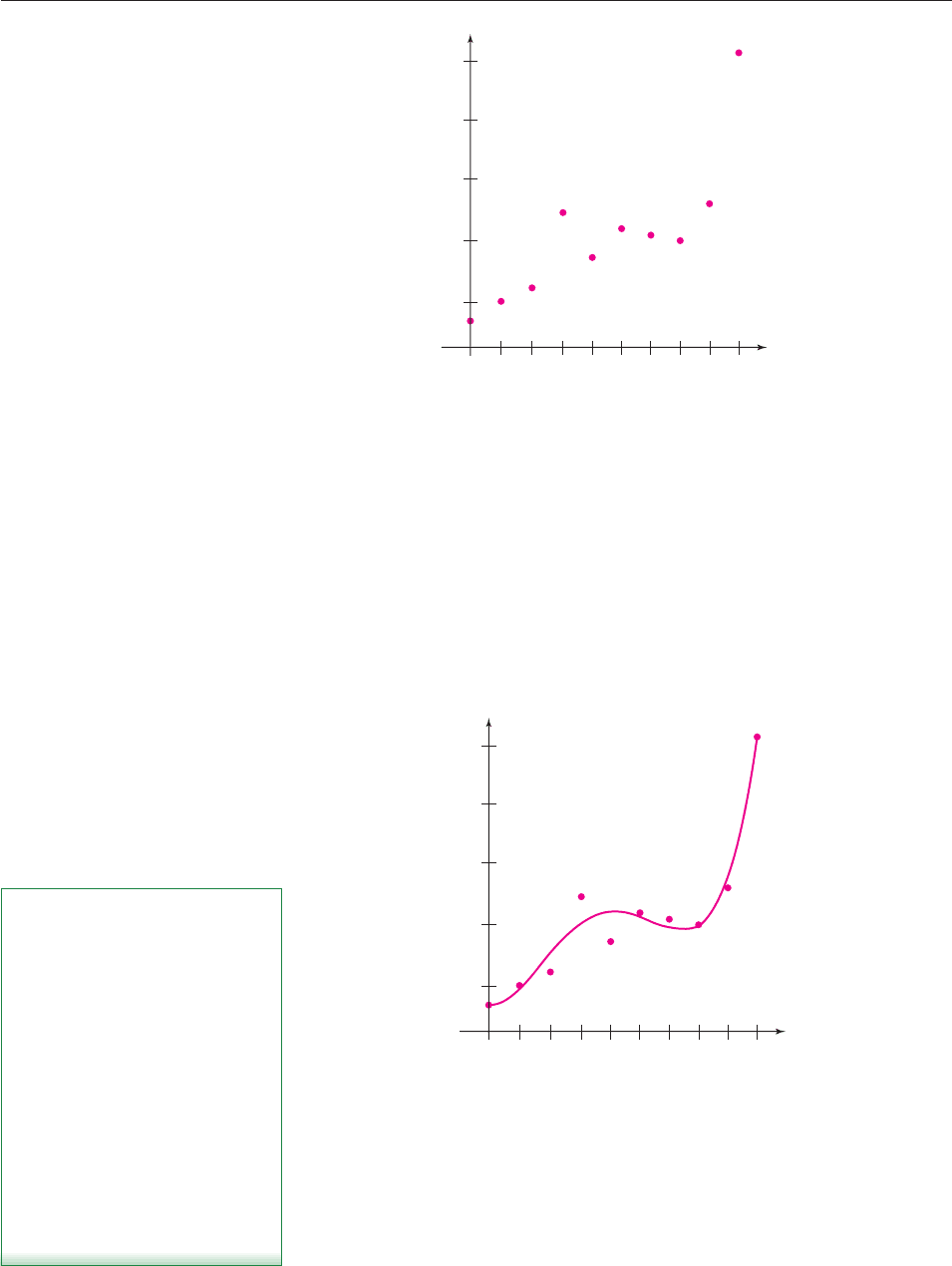
Since the data points suggest a curve that is concave upward on the left, concave
downward in the middle, and concave upward again on the right, a fourth-degree
polynomial might provide a reasonable model. We use the regression feature of a
calculator to find this model:
f (x) .00001547x
4
.0008969x
3
+ .01441x
2
.01676x .3672
The graph of f is shown in Figure 4–32.
SPECIAL TOPICS 4.4.A Polynomial Models 285
8401612 2420
Time since 1970
Gas price
28 3632
0.5
1
1.5
2.5
2
x
y
Figure 4–31
8401612 2420
Time since 1970
Gas price
28 3632
0.5
1
1.5
2.5
2
x
y
Figure 4–32
Although this function provides a reasonable model from 1970–2006, our knowl-
edge of polynomial graphs suggests that they may not be accurate in the future.
You can find the today’s average price of gasoline on the world-wide-web. Compare
the predicted value to the actual value. ■
NOTE
You must have at least three data
points for quadratic regression, at least
four for cubic regression, and at least
five for quartic regression. If you have
exactly the required minimum number
data points, no two of them can have
the same first coordinate. In this case,
the polynomial regression function will
pass through all of the data points (an
exact fit). When you have more than the
minimum number of data points re-
quired, the fit will generally be approxi-
mate rather than exact.
