Hungerford T.W., Shaw D.J. Contemporary Precalculus: A Graphing Approach
Подождите немного. Документ загружается.

EXAMPLE 6
The owner of a 20-unit apartment complex has found that each $50 increase in
monthly rent results in another vacant apartment. All units are now rented at $400
per month. How many $50 increases in rent will produce the largest possible
income for the owner?
SOLUTION Let x represent the number of $50 increases. Then the monthly
rent will be 400 50x dollars. Since one apartment goes vacant for each increase,
the number of occupied apartments will be 20 x. Then the owner’s monthly
income R(x) is given by
R(x) (number of apartments rented) (rent per apartment)
R(x) (20 x)(400 50x)
R(x) 50x
2
600x 8000
There are three ways to find the maximum possible income.
Algebraic Method. The graph of R(x) 50x
2
600x 8000 is a
downward-opening parabola (why?). The maximum income occurs at the vertex
of this parabola, that is, when
x
2a
b
2
(
60
5
0
0)
6
1
0
0
0
0
6.
Therefore, six increases of $50 will produce maximum income.
Graphical Method. Graphing R(x) 50x
2
600x 8000 and using a
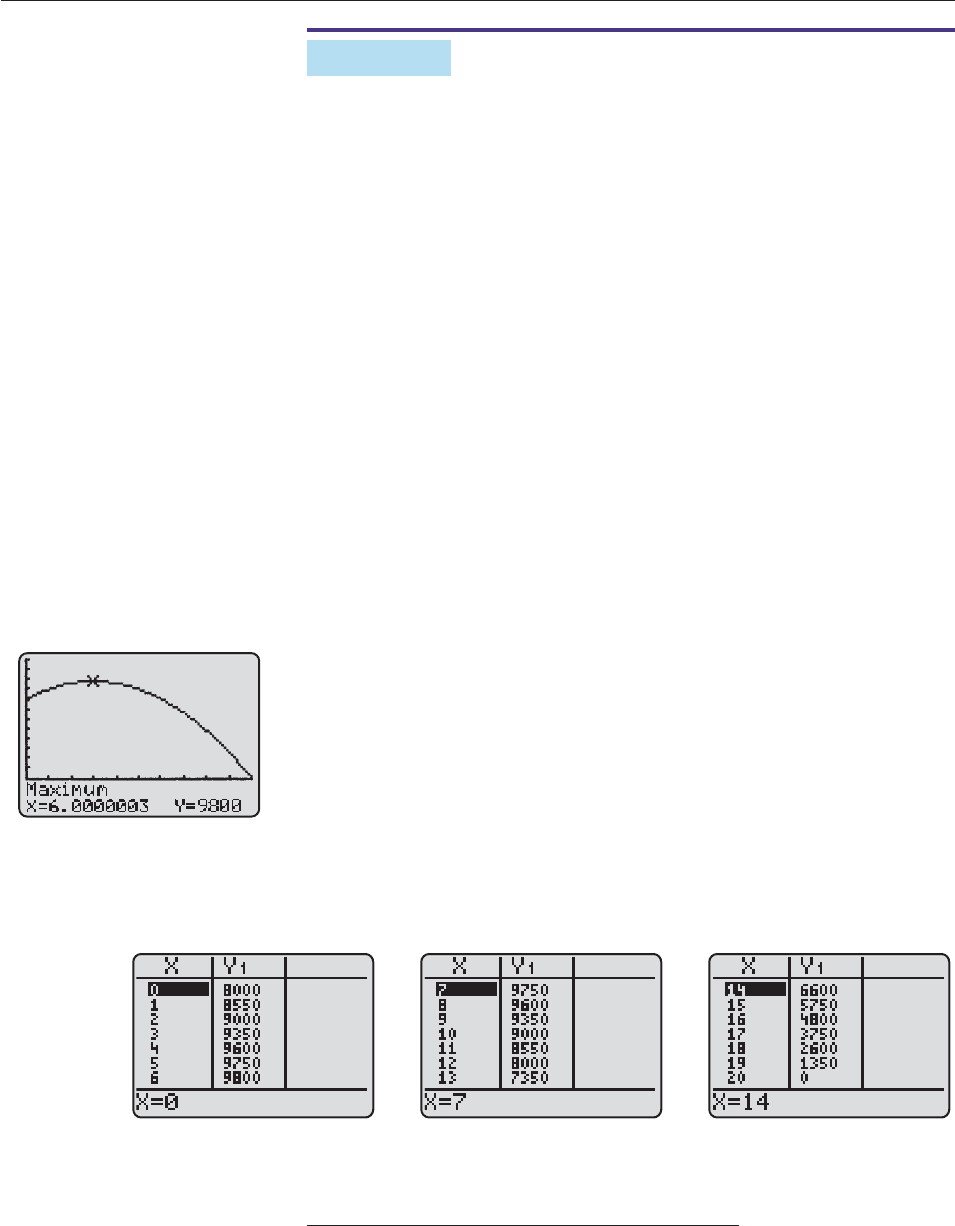
maximum finder to determine the coordinates of the vertex, as in Figure 4–6,
shows that maximum income of $9800 occurs when there are six rent increases.
Tabular Method. Make a table of values of R(x) for 0 x 20, as in Fig-
ure 4–7.* The table shows that the maximum income of $9800 occurs when
x 6. In this case, there will be 20 6 14 apartments rented at a monthly rent
of 400 6(50) $700. ■
246 CHAPTER 4 Polynomial and Rational Functions
12,000
20
0
Figure 4–6
Figure 4–7
*This method is feasible here because there are only 20 apartments, but it cannot be used when the
number of possibilities is very large or infinite.
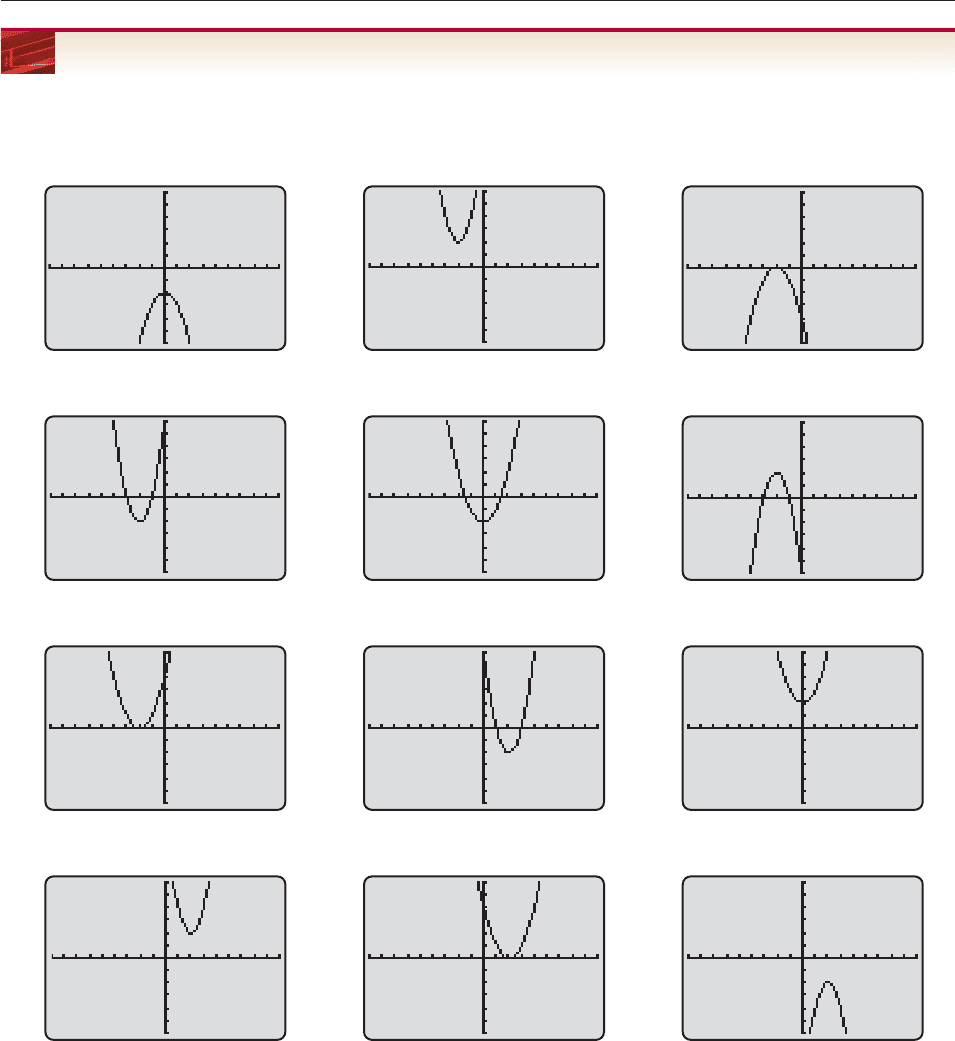
In Exercises 1–8, use the catalog of functions at the end of Section 3.3 and the information in this section to match each function
with its graph, which is one of those shown here.
9
6
−6
−9
9
6
−6
−9
9
6
−6
−9
9
6
−6
−9
9
6
−6
−9
9
6
−6
−9
9
6
−6
−9
9
6
−6
−9
9
6
−6
−9
9
6
−6
−9
9
6
−6
−9
9
6
−6
−9
A. B. C.
D. E. F.
G. H. I.
J. K. L.
SECTION 4.1 Quadratic Functions 247
EXERCISES 4.1
1. f (x) x
2
2 2. g(x) x
2
2
3. g(x) (x 2)
2
4. f (x) (x 2)
2
5. f (x) 2(x 2)
2
2 6. g(x) 2(x 2)
2
2
7. g(x) 2(x 2)
2
2 8. f (x) 2(x 2)
2
2
In Exercises 9–20, without graphing, determine the vertex of
the given parabola and state whether it opens upward or
downward.
9. f (x) 3(x 5)
2
2 10. g(x) 3(x 3)
2
5

11. y (x 2
)
2
p 12. h(x) x
2
1
13. f(x) 2x
2
16x 29 14. g(x) x
2
8x 1
15. h(x) x
2
3x 1 16. f (x) x
2
5x 7
17. y 4x
2
8x 1 18. y 3x
2
6x 1
19. f (x) 2x
2
3 20. g(x) x
2
6x 4
In Exercises 21–24, find
(a) The difference quotient of the function;
(b) The vertex of the function’s graph;
(c) The value of the difference quotient at the x-coordinate of
the vertex.
21. f (x) 3x
2
x 22. g(x) 2x
2
x 1
23. f (x) 2x
2
2x 1 24. g(x) 3x
2
4x 5
25. The graph of the quadratic function g is obtained from the
graph of f (x) x
2
by vertically stretching it by a factor of 2
and then shifting vertically 3 units downward. What is the
rule of the function g? What is the vertex of its graph?
26. The graph of the quadratic function g is obtained from the
graph of f (x) x
2
by shifting it horizontally 4 units to the
left, then vertically stretching it by a factor of 3, and then
shifting vertically 2 units upward. What is the rule of the
function g? What is the vertex of its graph?
27. If the graph of the quadratic function h is shifted vertically
4 units downward, then shrunk by a factor of 1/2, and then
shifted horizontally 5 units to the left, the resulting graph is
the parabola f (x) x
2
. What is the rule of the function h?
What is the vertex of its graph?
28. If the graph of the quadratic function h is shifted vertically
3 units upward, then reflected in the x-axis, and then shifted
horizontally 5 units to the right, the resulting graph is the
parabola f (x) x
2
. What is the rule of the function h? What
is the vertex of its graph?
In Exercises 29–32, find the rule of the quadratic function
whose graph satisfies the given conditions.
29. Vertex at (0, 0); passes through (2, 12)
30. Vertex at (0, 1); passes through (2, 7)
31. Vertex at (3, 4); passes through (3, 76)
32. Vertex at (4, 1); passes through (2, 11)
In Exercises 33–36, find the rule of the quadratic function
whose graph passes through the given points (one of which is
the vertex).
33. (0, 5), (1, 4), (2, 5)
34. (0, 11), (3, 2), (3, 38)
35. (0, 6), (1, 7), (2, 10)
36. (3.1, 4.1), (6.1, 13.1), (.9, 20.1)
37. Find the number b such that the vertex of the parabola
y x
2
bx c lies on the y-axis.
38. Find the number c such that the vertex of the parabola
y x
2
8x c lies on the x-axis.
39. If the vertex of the parabola f (x) x
2
bx c is at
(2, 4), find b and c.
40. If the vertex of the parabola f (x) x
2
bx 8 has sec-
ond coordinate 17 and is in the second quadrant, find b.
41. Find two numbers whose sum is 111 and whose product is
as large as possible.
42. Find two positive numbers whose sum is 111 and with the
sum of their squares as small as possible.
43. The Leslie Lahr Luggage Company has determined that its
profit on its Luxury ensemble is given by
p(x) 1600x 4x
2
50,000,
where x is the number of units sold.
(a) What is the profit on 50 units? On 250 units?
(b) How many units should be sold to maximize profit? In
that case, what will be the profit on each unit?
(c) What is the largest number of units that can be sold
without a loss?
44. On the basis of data from past years, a consultant informs
Bob’s Bicycles that its profit from selling x bicycles is given
by the function
p(x) 250x x
2
/4 15,000.
(a) How much profit do they make by selling 100 bicycles?
By selling 400 bicycles?
(b) How many bicycles should be sold to maximize profit?
In that case, what will be the profit per bicycle?
45. During the Civil War, the standard heavy gun for coastal
artillery was the 15-inch Rodman cannon, which fired a
330-pound shell. If one of these guns is fired from the top of
a 50-foot-high shoreline embankment, then the height of the
shell above the water (in feet) can be approximated by the
function
p(x) .0000167x
2
.23x 50,
where x is the horizontal distance (in feet) from the foot of the
embankment to a point directly under the shell. How high
does the shell go, and how far away does it hit the water?
46. The Golden Gate Bridge is supported by two huge cables
strung between the towers at each end of the bridge. The
function
f (x) .0001193x
2
.50106x 526.113
gives the approximate height of the cables above the road-
way at a point on the road x feet from one of the towers. The
cables touch the road halfway between the two towers. How
far apart are the towers?
47. The braking distance (in meters) for a car with excellent
brakes on a good road with an alert driver can be modeled
by the quadratic function B(s) .01s
2
.7s, where s is the
car’s speed in kilometers per hour.
(a) What is the braking distance for a car traveling 30 kilo-
meters per hour? For one traveling 100 kilometers per
hour?
248 CHAPTER 4 Polynomial and Rational Functions
(b) If the car takes 60 meters to come to a complete stop,
what was its speed?
48. Jack throws a baseball. Its height above the ground (in feet)
is given by
h(x) .0013x
2
.26x 5.5
where x is the distance (in feet) from Jack to a point on the
ground directly below the ball.
(a) How far from Jack is the ball when it reaches the high-
est point on its flight? How high is the ball at that point?
(b) How far from Jack does the ball hit the ground?
In Exercises 49–52, use the formula for the height h of an object
that is traveling vertically (subject only to gravity) at time t:
h 16t
2
v
0
t h
0
,
where h
0
is the initial height and v
0
is the initial velocity; t is
measured in seconds and h in feet.
49. A ball is thrown upward from the top of a 96-foot-high tower
with an initial velocity of 80 feet per second. When does the
ball reach its maximum height and how high is it at that time?
50. A penny is dropped from the top of Bank of America building
in Atlanta, Georgia. How long does it take to reach the ground?
(Assume the Bank of America building is 1024 feet high.)
51. A ball is thrown upward from a height of 5 feet with an ini-
tial velocity of 11 feet per second. Find its maximum height.
52. A bullet is fired upward from ground level with an initial
velocity of 1800 feet per second. How high does it go?
53. The sum of the height h and the base b of a triangle is 30. What
height and base will produce a triangle of maximum area?
54. A gutter is to be made by bending up the edge of a 20-inch-
wide piece of aluminum. What depth should the gutter be to
have the maximum possible cross-sectional area?
55. A field bounded on one side by a river is to be fenced
on three sides so as to form a rectangular enclosure. If
200 feet of fencing is to be used, what dimensions will yield
an enclosure of the largest possible area?
20
xx
56. A rectangular box (with top) has a square base. The sum of
the lengths of its 12 edges is 8 feet. What dimensions should
the box have so that its surface area is as large as possible?
57. A gardener wants to use 130 feet of fencing to enclose a rec-
tangular garden and divide it into two plots, as shown in the
figure. What is the largest possible area for such a garden?
58. A rectangular garden next to a building is to be fenced on
three sides. Fencing for the side parallel to the building
costs $80 per foot, and material for the other two sides costs
$20 per foot. If $1800 is to be spent on fencing, what are the
dimensions of the garden with the largest possible area?
59. At Middleton Place, a plantation near Charleston, South
Carolina, there is a “joggling board” that was once used for
courting. A young girl would sit at one end, her suitor at the
other end, and her mother in the center. The mother would
bounce on the board, thus causing the girl and her suitor to
move closer together. A joggling board is 8 feet long and an
average mother sitting at its center causes the board to
deflect 2 inches, as shown in the figure. The shape of the
deflected board is parabolic.
(a) Find the equation of the parabola, assuming that the
joggling board lies on the x-axis with its center at the
origin.
(b) How far from the center of the board is the deflection 1
inch?
60. A salesperson finds that her sales average 40 cases per store
when she visits 20 stores a week. Each time she visits an ad-
ditional store per week, the average sales per store decrease
by 1 case. How many stores should she visit each week if
she wants to maximize her sales?
61. A potter can sell 120 bowls per week at $5 per bowl. For
each 50¢ decrease in price, 20 more bowls are sold. What
price should be charged to maximize sales income?
62. A vendor can sell 200 souvenirs per day at a price of $2
each. Each 10¢ price increase decreases the number of sales
by 25 per day. Souvenirs cost the vendor $1.50 each. What
price should be charged to maximize the profit?
63. When a basketball team charges $10 per ticket, average
attendance is 500 people. For each 25¢ decrease in ticket
price, average attendance increases by 30 people. What
should the ticket price be to ensure maximum income?
2 inches
8 feet
SECTION 4.1 Quadratic Functions 249
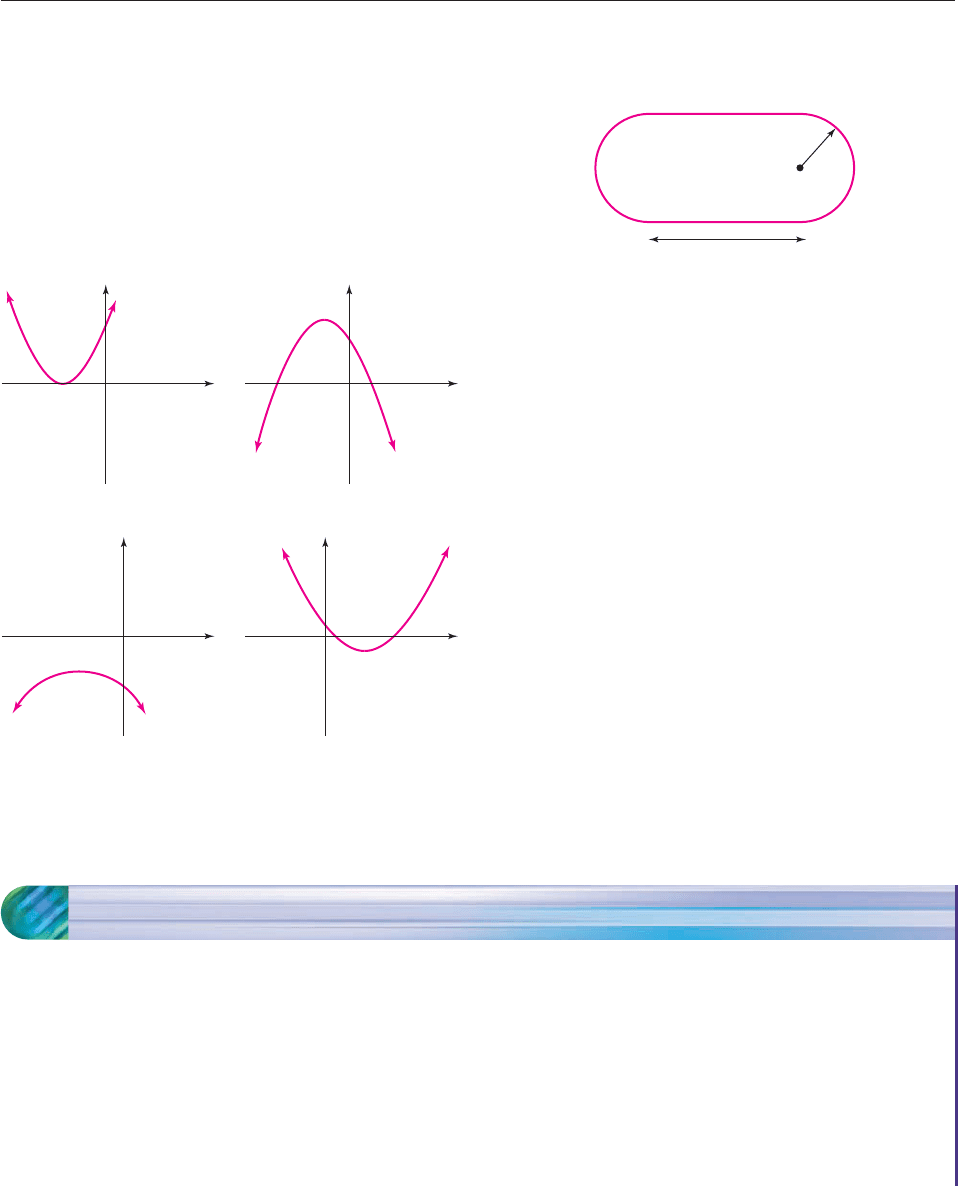
THINKERS
64. The discriminant of a quadratic function
f (x) ax
2
bx c
is the number b
2
4ac. For each of the discriminants listed,
state which graphs could possibly be the graph of f.
(a) b
2
4ac 25
(b) b
2
4ac 0
(c) b
2
4ac 49
(d) b
2
4ac 72
x
y
x
y
x
y
x
y
(ii)
(iii) (iv)
(i)
250 CHAPTER 4 Polynomial and Rational Functions
65. We are designing a track for a 200 meter race. The shape of
the track will be two x-meter, long straight stretches along
with two semicircular caps of radius r, as shown below:
Inside the track, we are going to have to plant grass, pull
weeds, etc. So we would like to minimize the total area
of the track. What is the minimum possible area? [Hint:
Find an expression for the area, and get it in terms of one
variable.]
66. According to the “logistic growth” model, the rate at which
a population of bunnies grows is a function of x, the number
of bunnies there already are
f(x) kx(C x) bunnies/year
where C 0 is the “carrying capacity” of the bunnies’ en-
vironment and k is a positive constant that can be deter-
mined experimentally. If f(x) is big, that means the bunny
population is growing quickly. If f(x) is negative, it means
the bunny population is declining.
(a) What bunny populations will yield a growth rate of
zero? (These are called “stable populations.”)
(b) For what bunny population is the growth rate largest?
(c) What bunny populations will yield a positive growth
rate?
x
r
■ Recognize the algebraic forms of a polynomial.
■ Use the Division Algorithm.
■ Apply the Remainder Theorem.
■ Apply the Factor Theorem.
■ Find the rule of a polynomial with given degree and
roots.
■ Determine the maximum possible number of roots a
polynomial may have.
Informally, a polynomial is an algebraic expression such as
x
3
6x
2
1
2
or x
15
x
10
7orx 6.7 or 12.
4.2 Polynomial Functions
Section Objectives

Formally, a polynomial in x is an algebraic expression that can be written in the
form
a
n
x
n
a
n1
x
n1
a
3
x
3
a
2
x
2
a
1
x a
0
,
where n is a nonnegative integer, x is a variable,* and each of a
0
, a
1
, . . . , a
n
is a
constant, called a coefficient. The coefficient a
0
is called the constant term. A
polynomial that consists only of a constant term, such as 12, is called a constant
polynomial. The zero polynomial is the constant polynomial 0.
The exponent of the highest power of x that appears with nonzero coefficient
is the degree of the polynomial, and the nonzero coefficient of this highest power
of x is the leading coefficient. For example,
Leading Constant
Polynomial Degree Coefficient Term
6x
7
4x
3
5x
2
7x 10 7 6 10
x
3
310
12 (think of this as 12x
0
)01212
0x
9
2x
6
3x
7
x
8
2x 48 1 4
The degree of the zero polynomial is not defined since no exponent of x occurs
with nonzero coefficient.
EXAMPLE 1
Which of the following are polynomials?
(a) x
2
x
3
2x x
4
(b) 3x
4
2x
2
1
x
3
(c) (x
2
5)(3x
2
2)
(d) x
2
3x 5
x
(e) x
2
3x p
3
(f) x x
3/2
1
SOLUTION
(a) x
2
x
3
2x x
4
is a polynomial. The order in which we write the terms
doesn’t change whether or not an expression is a polynomial.
(b) 3x
4
2x
2
1
x
3 is not a polynomial. The term
1
x
cannot be written in
the form ax
n
for any positive integer n.
(c) (x
2
5)(3x
2
2) is a polynomial. Its expanded form is 3x
4
13x
2
10.
(d) x
2
3x 5
x
is not a polynomial. The exponents in a polynomial cannot be
variables.
(e) x
2
3x p
3
is a polynomial. p
3
is just a constant.
(f) x x
3/2
1 is not a polynomial. The exponents of x must be whole numbers,
and 3/2 is not a whole number. ■
SECTION 4.2 Polynomial Functions 251
*Any letter may be used as the variable in a polynomial.
A polynomial function is a function whose rule is given by a polynomial,
such as f (x) x
5
3x
2
2. First-degree polynomial functions, such as
g(x) 3x 4, are called linear functions, and, as we saw in Section 4.1,
second-degree polynomial functions are called quadratic functions.
POLYNOMIAL ARITHMETIC
You should be familiar with addition, subtraction, and multiplication of polyno-
mials, which are presented in the Algebra Review Appendix. Long division of
polynomials is quite similar to long division of numbers, as we now see.
EXAMPLE 2
Divide 8x
3
2x
2
1 by 2x
2
x.
SOLUTION We set up the division in the same way that is used for numbers.
Divisor 2x
2
x 8x
3
2x
2
1 Dividend
Begin by dividing the first term of the divisor (2x
2
) into the first term of the div-
idend (8x
3
) and putting the result
namely,
8
2
x
x
3
2
4x
on the top line, as shown
below. Then multiply 4x times the entire divisor, put the result on the third line,
and subtract
4x
Partial Quotient
2x
2
x 8x
3
2x
2
1
8x
3
4x
2
4x(2x
2
x)
6x
2
1 Subtraction*
Now divide the first term of the divisor (2x
2
) into 6x
2
and put the result
6
2
x
x
2
2
3
on the top line, as shown below. Then multiply 3 times the entire divisor,
put the result on the fifth line, and subtract
The division process stops when the remainder is 0 or has smaller degree than the
divisor, which is the case here. ■
252 CHAPTER 4 Polynomial and Rational Functions
*If this subtraction is confusing, write it out horizontally and watch the signs:
(8x
3
2x
2
1) (8x
3
4x
2
) 8x
3
2x
2
1 8x
3
4x
2
6x
2
1.
4x 3 Quotient
2x
2
x 8x
3
2x
2
1
8x
3
4x
2
4x(2x
2
x)
6x
2
1 Subtraction
6x
2
3x 3(2x
2
x)
Remainder 3x 1 Subtraction

We review the process of checking a long division problem by computing
4509/31:
145
31 4509
Check: 145 Quotient
31 31 Divisor
140 4495
124 14 Remainder
169 4509 Dividend
155
14
We can summarize this process in one line:
Divisor
Quotient Remainder Dividend.
The same thing works for division of polynomials, as you can see by examining
the division problem from Example 2.
Divisor
Quotient Remainder
(2x
2
x)
(4x 3) (3x 1) (8x
3
2x
2
3x) (3x 1)
8x
3
2x
2
1
Dividend
This fact is so important that it is given a special name and a formal statement.
SECTION 4.2 Polynomial Functions 253
The Division
Algorithm
If a polynomial f (x) is divided by a nonzero polynomial h(x), then there is
a quotient polynomial q(x) and a remainder polynomial r(x) such that
Dividend Divisor
Quotient Remainder
f (x) h(x) q(x) r(x),
where either r (x) 0 or r (x) has degree less than the degree of the
divisor h(x).
———
———
———
———
EXAMPLE 3
Show that 2x
2
1 is a factor of 6x
3
4x
2
3x 2.
SOLUTION We divide 6x
3
4x
2
3x 2 by 2x
2
1 and find that the
remainder is 0.
3x 2
2x
2
16x
3
4x
2
3x 2
6x
3
3x
4x
2
2
4x
2
2
0.
TECHNOLOGY TIP
The TI-89 does polynomial division
(use PROPFRAC in the ALGEBRA
menu). It dispays the answer as the
sum of a fraction and a polynomial:
Re
D
m
iv
a
i
i
s
n
o
d
r
er
Quotient.
Since the remainder is 0, the Division Algorithm tells us that
Dividend Divisor
Quotient Remainder
6x
3
4x
2
3x 2 (2x
2
1)(3x 2) 0
(2x
2
1)(3x 2).
Therefore, 2x
2
1 is a factor of 6x
3
4x
2
3x 2, and the other factor is the
quotient 3x 2. ■
Example 3 illustrates this fact.
254 CHAPTER 4 Polynomial and Rational Functions
Remainders
and Factors
The remainder in polynomial division is 0 exactly when the divisor is a fac-
tor of the dividend. In this case, the quotient is the other factor.
REMAINDERS AND ROOTS
When a polynomial f (x) is divided by a first-degree polynomial, such as x 3 or
x 5, the remainder is a constant (because constants are the only polynomials of
degree less than 1). This remainder has an interesting connection with the values
of the polynomial function f (x).
EXAMPLE 4
Let f (x) x
3
2x
2
4x 5.
(a) Find the quotient and remainder when f (x) is divided by x 3.
(b) Find f (3).
SOLUTION
(a) Using long division, we have
x
2
x 1
x 3 x
3
2x
2
4x 5
x
3
3x
2
x
2
4x 5
x
2
3x
x 5
x 3
2.
Therefore, the quotient is x
2
x 1, and the remainder is 2.
(b) Using the Division Algorithm, we can write the dividend
f (x) x
3
2x
2
4x 5 as
Dividend Divisor
Quotient Remainder
f (x) (x 3)(x
2
x 1) 2.
Hence,
f (3) (3 3)(3
2
3 1) 2 0 2 2.
NOTE
When the divisor is a first-degree poly-
nomial such as x 3, there is a con-
venient shorthand method of division,
called synthetic division. See Special
Topics 4.2.A for details.

Note that the number f (3) is the same as the remainder when f (x) is divided
by x 3. ■
The argument used in Example 4 to show that f (3) is the remainder when f (x) is
divided by x 3 also works in the general case and proves this fact.
SECTION 4.2 Polynomial Functions 255
Remainder
Theorem
If a polynomial f (x) is divided by x c, then the remainder is the number
f (c).
EXAMPLE 5
To find the remainder when f (x) x
79
3x
24
5 is divided by x 1, we apply
the Remainder Theorem with c 1. The remainder is
f (1) 1
79
3
1
24
5 1 3 5 9. ■
EXAMPLE 6
To find the remainder when f (x) 3x
4
8x
2
11x 1 is divided by x 2, we
must apply the Remainder Theorem carefully. The divisor in the theorem is
x c, not x c. So we rewrite x 2 as x (2) and apply the theorem with
c 2. The remainder is
f (2) 3(2)
4
8(2)
2
11(2) 1 48 32 22 1 5. ■
If f (x) is a polynomial, then a solution of the equation f (x) 0 is called a root
or zero of f (x). Thus, a number c is a root of f (x) if f (c) 0. A root that is a real
number is called a real root. For example, 4 is a real root of the polynomial
f (x) 3x 12 because f (4) 3
4 12 0. There is an interesting connection
between the roots of a polynomial and its factors.
EXAMPLE 7
Let f (x) x
3
4x
2
2x 3.
(a) Show that 3 is a root of f (x).
(b) Show that x 3 is a factor of f (x).
SOLUTION
(a) Evaluating f (x) at 3 shows that
f (3) 3
3
4(3
2
) 2(3) 3 0.
Therefore, 3 is a root of f (x).
(b) If f (x) is divided by x 3, then by the Division Algorithm, there is a quotient
polynomial q(x) such that
f (x) (x 3)q(x) remainder.
