Hungerford T.W., Shaw D.J. Contemporary Precalculus: A Graphing Approach
Подождите немного. Документ загружается.

or $21,446. Because 2008 is outside the range of the data points, this figure
might not be as accurate as the estimate for 2003, which lies within the data
range. ■
EXAMPLE 5
The death rates from heart disease (per 100,000 population) are given in the table.*
126 CHAPTER 2 Graphs and Technology
Find the linear regression model for this data. If the model fits the data well, use
it to estimate the death rates in 1998 and 2008.
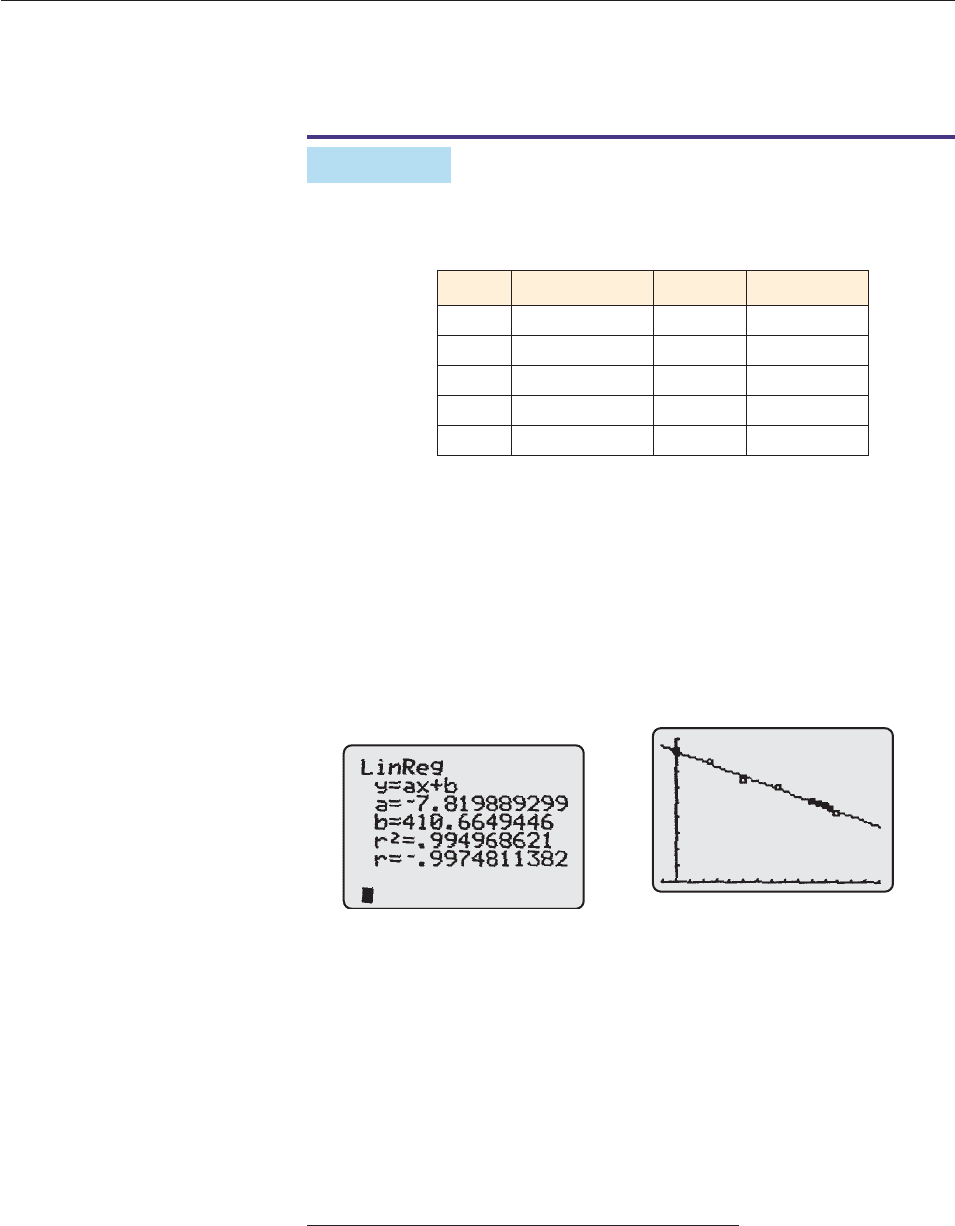
SOLUTION We let x 0 correspond to 1980, enter the data points in the
statistical editor of a calculator, and find the equation of the regression line (Fig-
ure 2–72). Since r .98, the data is negatively correlated and the model fits it
very well, as the graph confirms (Figure 2–73).
To find the death rates in 1998 and 2008, we evaluate the equation when x 18
and x 28.
†
y 7.8199x 410.6649 y 7.8199x 410.6649
7.8199(18) 410.6649 7.8199(28) 410.6649
269.9 191.7
So the death rates are estimated to be 269.9 in 1998 and 191.7 in 2008. ■
*U.S. National Center for Health Statistics.
†
The coefficients are rounded for easier reading; this doesn’t affect the answer here.
Year Death Rate Year Death Rate
1980 412.1 2001 247.8
1985 375.0 2002 240.8
1990 321.8 2003 232.3
1995 296.3 2004 217.5
2000 257.6
Figure 2–72
450
0
230
Figure 2–73
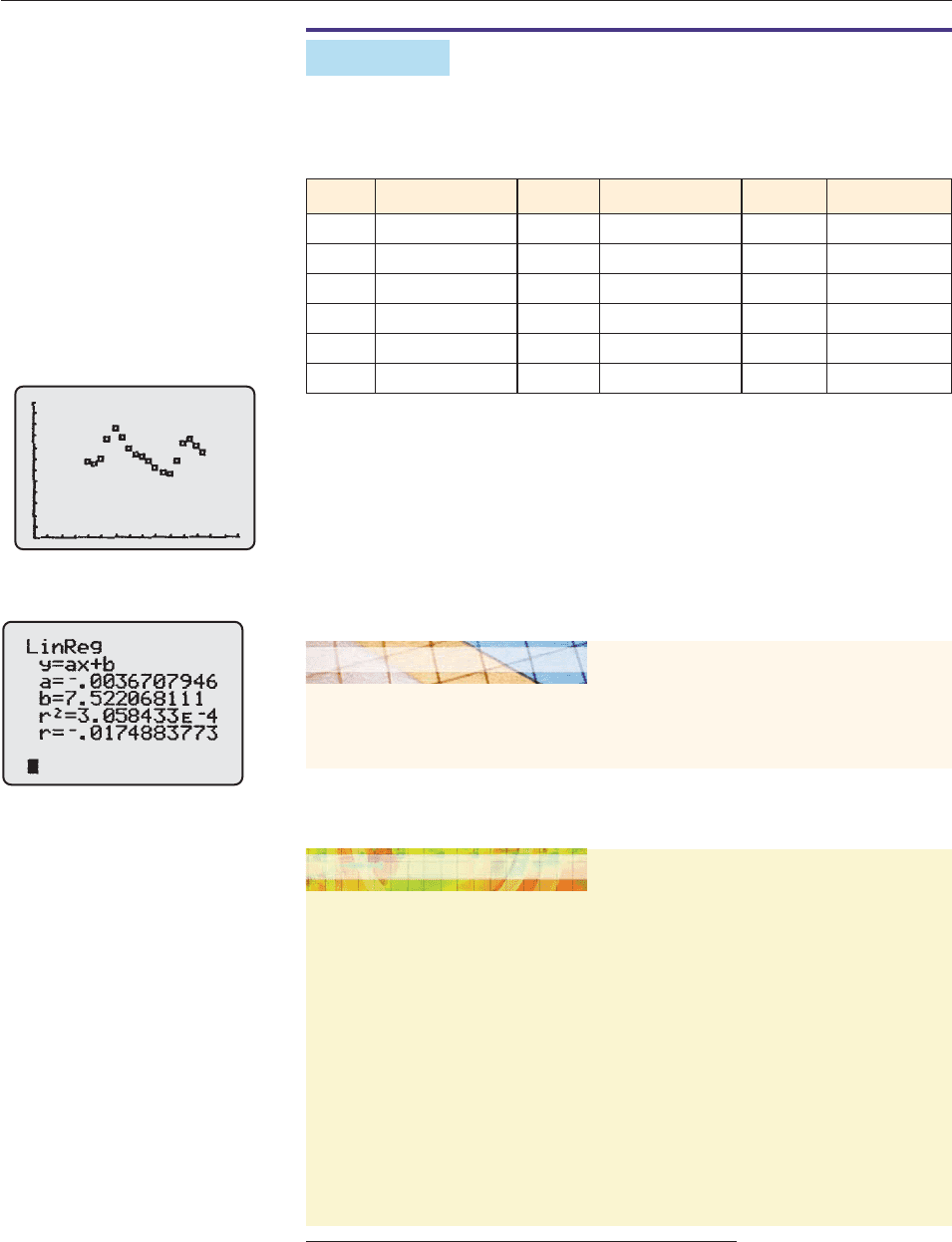
SOLUTION Let x 0 correspond to 1980. After entering the data points as
two lists in the statistics editor, you can test it graphically or analytically.
Graphical: The scatter plot of the data points in Figure 2–74 does not have a
linear pattern (unemployment tends to rise and fall).
Analytical: Linear regression (Figure 2–75) produces an equations whose
correlation coefficient that is almost 0, namely, r .017. This indicates that
there is no correlation and that the regression line is a very poor fit for the data.
Therefore, a linear equation is not a good model for this data. ■
SECTION 2.5 Linear Models 127
Year Unemployed Year Unemployed Year Unemployed
1988 6.701 1994 7.996 2000 5.692
1989 6.528 1995 7.404 2001 6.801
1990 7.047 1996 7.236 2002 8.378
1991 8.628 1997 6.739 2003 8.774
1992 9.613 1998 6.210 2004 8.149
1993 8.940 1999 5.880 2005 7.591
The following Technology Tip may be helpful for learning how to use the
regression feature of your calculator.
12
0
030
Figure 2–74
Figure 2–75
TECHNOLOGY TIP
If the data points have been entered in the statistics editor as lists L
1
and L
2
, use these TI com-
mands to find the least squares regression line and store its equation as y
1
in the equation memory:
TI-84+: STAT CALC LinReg L
1
, L
2
, Y
1
TI-86: STAT CALC Lin R L1, L2, y
1
TI-89: From the Data Editor, choose CALC (F
5
); enter LIN REG as the CALCULATION TYPE, list C
1
as
x, list C
2
as y, and choose y
1
(x) in STORE REGEQ.
To graph the equation and the data points (assuming Plot 1 is ON and set for L
1
and L
2
), press
GRAPH or DRAW.
On HP-39gs, plot the data points, press MENU FIT to graph the regression line and SYMB to
see its equation.
On Casio 9850, plot the data points, press X for the equation of the regression line and
DRAW for its graph.
Enter the data from Example 6 in the statistics editor of your calculator. Graph the
data points. Graph the least squares regression line on the same screen to see how
poorly it fits the data.
GRAPHING EXPLORATION
*U.S. Bureau of Labor Statistics.
EXAMPLE 6
The number of unemployed people in the labor force (in millions) for 1988–2005
is shown in the table.* Determine whether a linear equation is a good model for
this data.
128 CHAPTER 2 Graphs and Technology
EXERCISES 2.5
In Exercises 1–4, two linear models are given for the data. For
each model,
(a) Find the residuals and their sum;
(b) Find the sum of the squares of the residuals;
(c) Determine which model is the better fit.
1. The weekly amount spent on advertising and the weekly
sales revenue of a small store over a five-week period are
shown in the table. Two models are y x and y .5x 1.5.
2. Advertising expenditures in the United States (in billions of
dollars) in selected years are shown in the table.* Two
models are y 12x 215 and y 11x 218, where x 0
corresponds to 2000.
3. The table gives the consumer price index (CPI) in April of
selected years.
†
Two models are y 4.9x 170 and
y 5x 171, where x 0 corresponds to 2000.
4. Revenues for U.S. public elementary and secondary schools
(in billions of dollars) in the fall of selected years are shown
in the table.
‡
Two models are
y 21x 370 and y 21.6x 372,
where x 0 corresponds to 2000.
5. The regression model for GE’s profits in Example 3 on
page 123 (with coefficients rounded) was y .71x 13.05.
Compute the sum of the squares of its residuals and verify
that this model is better than either of those in Example 2.
Advertising Expenditures x 12345
(in hundreds of dollars)
Sales Revenue y 22335
(in thousands of dollars)
Year 2001 2002 2003 2004
Amount 231 237 245 264
Year 2000 2002 2003 2004
Revenues 370 416 444 453
Year 2000 2002 2004 2006
CPI 171.3 179.8 188 201.5
*Advertising Age.
†
U.S. Bureau of Labor Statistics.
‡
Statistical Abstract of the United States: 2006.
In Exercises 6–9, determine whether the given scatter plot of
the data indicates that there is a positive correlation, a nega-
tive correlation, or very little correlation.
6.
7.
8.
9.
In Exercises 10–15, construct a scatter plot for the data and
answer these questions: (a) Does the data appear to be linear?
(b) If so, is there a positive or negative correlation?
10. Consumer debt (in trillions of dollars) is shown in the
table.* Let x 0 correspond to 1990.
11. The U.S. gross domestic product (GDP) is the total value of
all goods and services produced in the United States. The
table shows the GDP in billions of 2000 dollars.
†
Let x 0
correspond to 1990.
y
x
y
x
y
x
y
x
Year 1995 2000 2002 2003 2004
Debt 1.1 1.7 1.9 2 2.1
*Federal Reserve Bulletin. The amounts are primarily credit card
balances; home mortgages are not included.
†
U.S. Bureau of Economic Analysis.
SECTION 2.5 Linear Models 129
Year 1990 1995 1998 2000 2002 2004
GDP 7113 8032 9067 9817 10,075 10,842
Age 30 35 40 45 50
Premium 6.48 6.52 6.78 7.88 9.93
Age 55 60 65 70
Premium 12.69 16.71 23.67 36.79
Month Feb April June Aug Oct Dec
Temperature 27.3 47.5 67.5 70.3 52.7 30.9
Temperature (°C) Pressure (mm Hg)
0 4.6
10 9.2
20 17.5
30 31.8
40 55.3
50 92.5
60 149.4
70 233.7
80 355.1
90 525.8
100 760
12. In mid-2002, Grange Life Insurance advertised the following
monthly premium rates for a $50,000 term policy for a female
nonsmoker. Let x represent age and y the monthly premium.
13. The table shows the average monthly temperature (in
degrees Fahrenheit) in Cleveland, Ohio.* Let x 2 corre-
spond to February, x 4 to April, etc.
14. The vapor pressure y of water depends on the temperature x,
as given in the table.
15. The table shows the U.S. Bureau of Census population data
for St. Louis, Missouri. Let x 0 correspond to 1950.
Year Population
1950 856,796
1970 622,236
1980 452,801
1990 396,685
2000 348,189
2005 352,572
In Exercises 16–26, use linear regression to find the requested
linear model.
16. The table shows the median time (in months) for the U.S.
Food and Drug Administration to approve a generic drug.
(a) Make a scatter plot of the data, with x 0 correspon-
ding to 1990.
(b) Find a linear model for the data.
(c) Assume that the model remains accurate and find the
median approval time in 2010.
17. The table shows the size of a room air conditioner (in BTUs)
needed to cool a room of the given area (in square feet).
(a) Find a linear model for the data.
(b) Use the model to find the number of BTUs required to
cool a rooms of size 150 sq ft, 280 sq ft, and 420 sq ft.
How well do the model estimates agree with the actual
data values?
(c) Use the model to estimate how many BTUs are needed
to cool a 235 sq ft room. If air conditioners are available
only with the BTU choices in the table, which size
should be chosen?
18. Enrollment in public colleges (in thousands) in selected
years is shown in the table on next page.*
Year Median Approval Time
1997 19.3
1998 18
1999 18.6
2000 18.2
2001 18.1
2002 18.2
2003 17
2004 15.7
Room Size BTUs
150 5000
175 5500
215 6000
250 6500
280 7000
310 7500
350 8000
370 8500
420 9000
450 9500
*Data and projections from the U.S. National Center for Education
Statistics.
*National climatic Data Center.
130 CHAPTER 2 Graphs and Technology
(a) Find a linear model for this data, with x 0 correspon-
ding to 2000.
(b) Use the model to estimate public college enrollment in
2005 and 2010.
(c) According to this model, when will public college
enrollment reach 21 million?
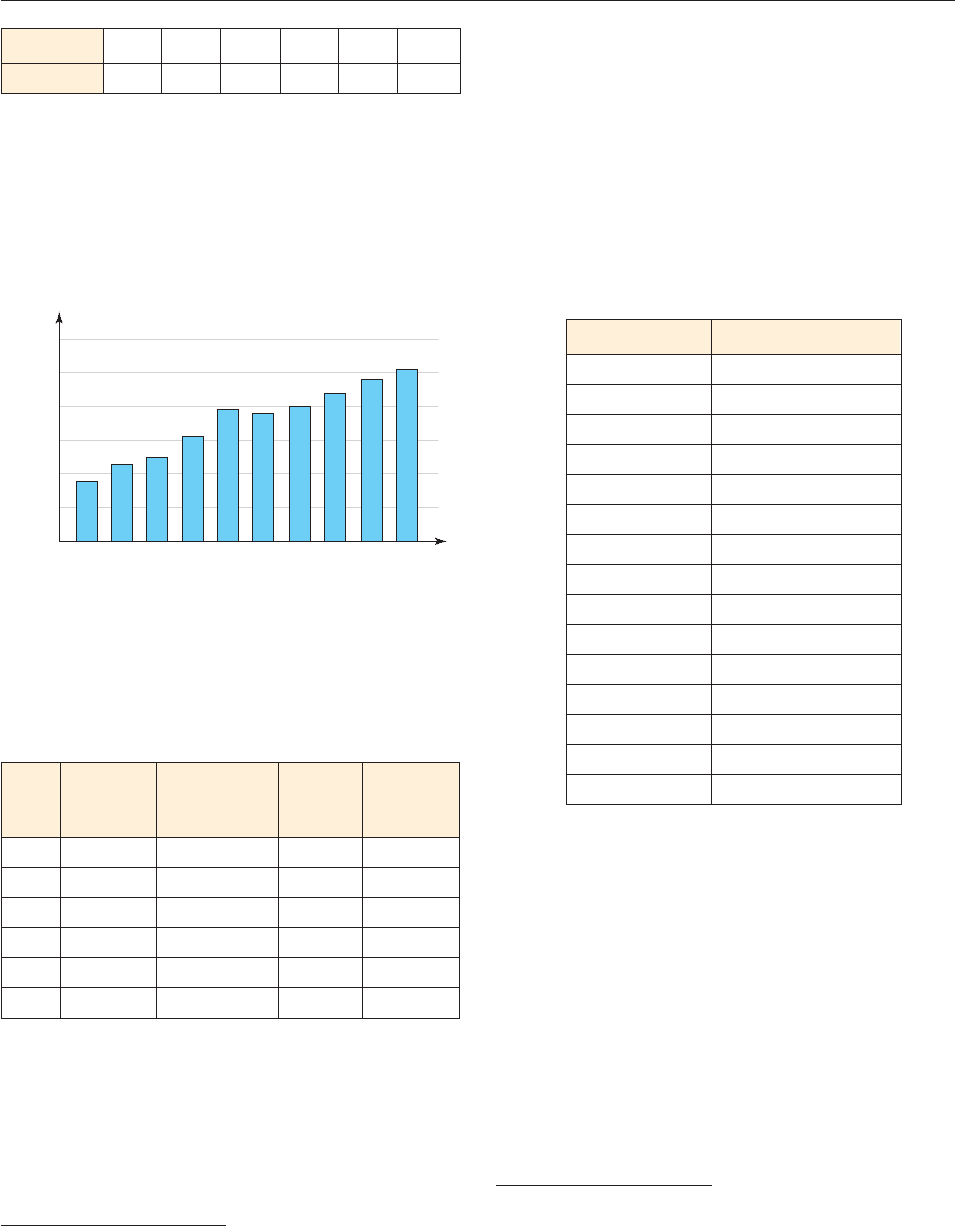
19. The graph shows Intel’s expenditures on research and
development (in billions of dollars) over a ten-year period.*
(a) List the data points, with x 6 corresponding to 1996.
(b) Find a linear model for the data.
(c) If the trend shown continues, what will Intel spend on
research and development in 2010?
In Exercises 20 and 21, use the following table, which gives the
median weekly earnings of full-time workers 25 years and
older by their educational level.
†
20. (a) Find linear models for the median weekly earnings of
full-time workers 25 years and older who did not grad-
uate from high school and for those who graduated
from high school, but did not attend college. Let x 0
correspond to 2000.
(b) Estimate the median weekly income for each group in
part (a) in 2009.
1
0
2
4
5
6
3
’96 ’97 ’98 ’99 ’00
’01
1.8
2.3
2.5
3.1
3.9
3.8
’02 ’03
4.0
4.4
’04 ’05
4.8
5.1
Year 2000 2001 2002 2004 2006 2008
Enrollment 15,313 15,928 16,612 17,095 17,664 18,350
No High
School High School Some College
Year Diploma Graduate College Graduate
2000 $360 $506 $598 $896
2001 $378 $520 $621 $924
2002 $388 $536 $617 $941
2003 $396 $554 $622 $963
2004 $401 $574 $642 $986
2005 $412 $584 $654 $996
*Intel Corporation Annual Report, 2005.
†
U.S. Bureau of Labor Statistics.
21.
(a) Find linear models for the median weekly earnings of
full-time workers 25 years and older who attended col-
lege, but did not graduate, and those who graduated
from college. Let x 0 correspond to 2000.
(b) Use the models in Exercises 20(a) and 21(a) to deter-
mine the approximate yearly rate at which the median
weekly earnings of each of the four groups in the table
are increasing. What does this say about the value of
education?
22. The table shows the relationship between the temperature
(in degree Fahrenheit) and the rate at which the striped
ground cricket chirps.*
(a) Find a linear model for this data and lists its correlation
coefficient.
(b) Estimate the number of chirps per second at a tempera-
ture of 73°.
(c) If the chirping rate is 18 times per second, estimate the
temperature.
23. The table on the next page gives the life expectancy at birth
(in years) in selected years in the United States.
†
(a) Find a linear model for men’s life expectancy, with
x 70 corresponding to 1970.
(b) Do part (a) for women’s life expectancy.
(c) Suppose the models in parts (a) and (b) remain accurate
in the future. Will men’s life expectancy ever be the same
as women’s? If so, in what birth year will this occur?
*Source: The Songs of Insects by George W. Pierce. Cambridge, MA:
Harvard University Press, copyright © 1948 by the President and
Fellows of Harvard College.
†
U.S. Center for Health Statistics.
Temperature Chirps per second
88.6 20.0
71.6 16.0
93.3 19.8
84.3 18.4
80.6 17.1
75.2 15.5
69.7 14.7
82.0 17.1
69.4 15.4
83.3 16.2
79.6 15.0
82.6 17.2
80.6 16.0
83.5 17.0
76.3 14.4

CHAPTER 2 Review 131
24. The projected number of new cases of Alzheimer’s disease
(in thousands) in the United States in selected years is
shown in the table.*
(a) Find a linear model for this data, with x 0 correspon-
ding to 2000, and use it to estimate the number of new
cases in the years 2005, 2015, and 2025.
Birth Year
Life Expectancy
Men Women
1970 67.1 74.7
1975 68.8 76.6
1980 70 77.4
1985 71.1 78.2
1990 71.8 78.8
1995 72.5 78.9
1998 73.8 79.5
2000 74.3 79.7
2003 74.8 80.1
2005 74.9 80.7
*Data and projections from the Federal Aviation Administration.
†
Centers for Medicare and Medicaid Services.
*U.S. Center for Health Statistics.
Year 2000 2010 2020 2030 2040 2050
New Cases 400 467 489 600 800 956
Year 2000 2002 2004 2006 2008 2010
Amount $143 $175 $207 $231 $287 $351
Year 2002 2003 2004 2005 2006 2007 2008 2009
Passengers .63 .64 .69 .72 .77 .79 .8 .84
(b) Use the model to predict the years in which the number
of new cases will be 750,000 and 1,000,000.
25. The projected number of scheduled passengers on U.S.
commercial airlines (in billions) is given in the table.*
(a) Find a linear model for this data, with x 2 correspon-
ding to 2002.
(b) Estimate the number of passengers in 2012 and 1016.
26. During the current decade, the amount of money each
American spends annually on prescription drugs (in addi-
tion to the amounts paid by insurance) is projected to
increase, as shown in the table.
†
(a) Find a linear model for this data, with x 0 correspon-
ding to 2000.
(b) Use the model to estimate the amount each person will
spend on prescription drugs in 2005, 2007, and 2011.
(c) According to this model, in what year will each Ameri-
can spend $400 on prescription drugs?
Chapter 2 Review
IMPORTANT CONCEPTS
Section 2.1
Equation memory 79
Viewing window 80
Trace 81
Zoom 82
Standard viewing window 82
Decimal window 83
Square window 83
Maximum/minimum finder 84
Complete graph 85
Scatter plots and line graphs 87
Section 2.2
x-intercepts and equation
solutions 92
Solving equations graphically 93, 95
Graphical root finder 93
Graphical intersection finder 94
Equation solvers 96
Solution methods 99
Section 2.3
Guidelines for setting up applied
problems 101
Solving applied problems with
equations 104–111
Section 2.4
Solving optimization problems
114–118
Section 2.5
Mathematical model 120
Residual 122
Least squares regression line 123
Linear regression 123
Correlation coefficient 124
Positive and negative correlation 124

132 CHAPTER 2 Graphs and Technology
In Questions 1–6,
(a) Determine which of the viewing windows a–e shows a
complete graph of the equation.
(b) For each viewing window that does not show a complete
graph, explain why.
(c) Find a viewing window that gives a “better” complete
graph than windows a–e (meaning that the window is
small enough to show as much detail as possible, yet large
enough to show a complete graph).
(a) Standard viewing window
(b) 10 x 10, 200 y 200
(c) 20 x 20, 500 y 500
(d) 50 x 50, 50 y 50
(e) 1000 x 1000, 1000 y 1000
1. y .2x
3
.8x
2
2.2x 6
2. y x
3
11x
2
25x 275
3. y x
4
7x
3
48x
2
180x 200
4. y x
3
6x
2
4x 24
5. y .03x
5
3x
3
69.12x
6. y .00000002x
6
.0000014x
5
.00017x
4
.0107x
3
.2568x
2
12.096x
In Questions 7–10, sketch a complete graph of the equation,
and give reasons why it is complete.
7. y x
2
10 8. y x
3
x 4
9. y x 5
10. y x
4
x
2
6
In Questions 11–14, sketch a complete graph of the equation.
11. y x
2
13x 43 12. y x
13. y x 5 14. y 1/x
In Questions 15–22, solve the equation graphically. You need
only find solutions in the given interval.
15. x
3
2x
2
11x 6; [0, )
16. x
3
2x
2
11x 6; (, 0)
17. x
4
x
3
10x
2
8x 16; [0, )
18. 2x
4
x
3
2x
2
6x 2 0; (, 1)
19.
x
3
x
2
2
x
2
2x
3x
15
4
0; (10, )
20. 0; [0, )
21. x
3
2
x
2
3
x 5
0; [0, )
22. 1 2x
3x
2
4x
3
x
4
0; (5, 5)
23. A jeweler wants to make a 1-ounce ring consisting of gold
and silver, using $200 worth of metal. If gold costs $600 per
ounce and silver costs $50 per ounce, how much of each
metal should she use?
24. A calculator is on sale for 15% less than the list price. The
sale price, plus a 5% shipping charge, totals $210. What is
the list price?
3x
4
x
3
6x
2
2x
x
5
x
3
2
25. Karen can do a job in 5 hours, and Claire can do the same
job in 4 hours. How long will it take them to do the job
together?
26. A car leaves the city traveling at 54 mph. One-half hour
later, a second car leaves from the same place and travels at
63 mph along the same road. How long will it take for the
second car to catch up with the first?
27. A 12-foot-long rectangular board is cut in two pieces so that
one piece is four times as long as the other. How long is the
bigger piece?
28. George owns 200 shares of stock, 40% of which are in the
computer industry. How many more shares must he buy to
have 50% of his total shares in computers?
29. A square region is changed into a rectangular one by mak-
ing it 2 feet wider and twice as long. If the area of the rec-
tangular region is three times larger than the area of the
original square region, what was the length of a side of the
square before it was changed?
30. The radius of a circle is 10 inches. By how many inches
should the radius be increased so that the area increases by
5p square inches?
31. The cost of manufacturing x caseloads of ballpoint pens is
600
x
x
2
2
1
600x
dollars. How many caseloads should be manufactured to
have an average cost of $25? [Average cost was defined in
Exercise 21 of Section 2.4.]
32. An open-top box with a rectangular base is to be con-
structed. The box is to be at least 2 inches wide and twice as
long as it is wide and is to have a volume of 150 cubic
inches. What should the dimensions of the box be if the sur-
face area is to be
(a) 90 square inches? (b) as small as possible?
33. A farmer has 120 yards of fencing and wants to construct a
rectangular pen, divided in two parts by an interior fence, as
shown in the figure. What should the dimensions of the pen
be to enclose the maximum possible area?
34. The top and bottom margins of a rectangular poster are each
5 inches, and each side margin is 3 inches. The printed ma-
terial on the poster occupies an area of 400 square inches.
Find the dimensions that will use the least possible amount
of posterboard.
REVIEW QUESTIONS

CHAPTER 2 Review 133
35. A rectangle has one side on the x-axis, and its other two cor-
ners sit on the graph of y 9 x
2
, as shown in the figure.
What value of x gives a rectangle of maximum area?
36. The window in the figure has a rectangular bottom, with a
semicircle of radius r lying on top of it, and a perimeter of
40 feet. In order that the window have the maximum possi-
ble area, what should r and h be?
37. The table shows monthly premiums (as of 2002) for a
$100,000 term life insurance policy from Grange Life
Insurance for a male smoker.
h
r
y
y
x
x
y = 9 − x
2
(x, y)
0
In Questions 39–42, use linear regression to find the requested
linear model.
39. The table shows how the circumference (in inches) of a
white oak tree (the Illinois state tree) is related to the
approximate age of the tree (in years).*
y
x
(a)
y
x
(b)
y
x
(c)
y
x
(d)
y
x
(e)
Age Premium
25 $20.30
30 $20.39
35 $20.39
40 $22.05
45 $28.61
50 $41.65
55 $60.90
60 $85.58
65 $132.91
Circumference Approximate
(inches) Age (years)
58
10 16
20 32
30 48
40 64
50 80
60 95
80 127
100 159
*The table assumes that the circumference is measured 4.5 ft above
ground level.
(a) Make a scatter plot of the data, using x for age and y for
premiums.
(b) Does the data appear to be linear?
38. For which of the following scatter plots would a linear
model be reasonable? Which sets of data show positive
correlation, and which show negative correlation?

(a) Find a linear model that gives the age y in terms of the
circumference x.
(b) Find the approximate age of trees whose circumfer-
ences are 56 in and 68 in.
(c) What is the diameter of a tree that is 151 years old?
40. The table shows the average hourly earnings of production
workers in manufacturing.*
(a) Find a linear model for the data, with x 0
corresponding to 2000.
(b) Use the model to estimate the average hourly earnings
in 2001 and 2004. How do the estimates of the model
compare with the actual figures?
(c) Estimate the average hourly earnings in 2008.
41. The table shows the total amount of charitable giving
(in billions of dollars) in the United States in recent
years.
†
(a) Find a linear model for the data, with x 0 correspond-
ing to 1990.
(b) Estimate the amount of charitable giving in 1999 and
2006.
134 CHAPTER 2 Graphs and Technology
(a) Make a scatter plot of average SAT math score y and
percent x of students who took the SAT, with the data
points arranged in order of increasing values of x.
(b) Find a linear model for the data.
(c) What is the slope of your linear model? What does this
mean in the context of the problem?
(d) Here are the data on four additional states. How well
does the model match the actual figures for these
states?
*U.S. Bureau of Labor Statistics.
†
Statistical Abstract of the United States: 2006.
*The College Board.
Charitable
Year Giving
1994 119.2
1996 138.6
1998 177.4
2000 227.7
2001 229.0
2002 234.1
2003 240.7
Hourly
Year Earnings
2000 $14.00
2001 $14.53
2002 $14.95
2003 $15.35
2004 $15.67
2005 $16.11
Students Who Average Math
State Took SAT (%) Score
Connecticut 86 517
Delaware 74 502
Georgia 75 496
Idaho 21 542
Indiana 66 508
Iowa 5 608
Montana 31 540
Nevada 39 513
New Mexico 13 547
North Dakota 4 605
Ohio 29 543
Pennsylvania 75 503
South Carolina 64 499
Washington 55 534
Students Who Average Math
State Took SAT (%) Score
Alaska 52 519
Arizona 33 530
Hawaii 61 516
Oklahoma 7 563
(c) According to the model, in what year will charitable
giving reach $372 billion?
42. The table shows, for selected states, the percent of high
school students in the class of 2005 who took the SAT and
the average SAT math score.*
CHAPTER 2 Test 135
Chapter
2
Test
Sections 2.1 and 2.2
1. Find a viewing window (or windows) that shows a com-
plete graph of
y .02x
5
.32x
4
.78x
3
2.48x
2
3.44x 4.8.
Your graph should clearly show all peaks, valleys, and
intercepts.
2. Solve
x
2
7x
2
24x
x.
3. Find the highest point on the graph of
y .04x
4
.4x
3
.4x
2
.4x 26.
Round the coordinates of the point to four decimal places.
4. (a) How many real solutions does the equation
.3x
5
2x
3
x k 0
have when k 0?
(b) Find a value of k for which the equation has just one
real solution.
5. Find a square window that shows a complete graph of
x
2
4y
2
144.
6. Solve
x
3
x
2
2
x
2
x
4x
6
8
0.
7. The concentration of a certain medication y in the blood-
stream at time x hours is approximated by
y
.1x
3
50
0x
100
,
where y is measured in milligrams per liter. After two days
the medication has no effect.
(a) Find a viewing window that contains only those points on
the graph of the equation that are relevant to the situation.
(b) At what time is the concentration of the medicine the
highest and what is the concentration at that time?
Round your answers to three decimal places.
8. Solve: x
4
x
2
2x
1
0. Round your answers to
four decimal places.
Sections 2.3 and 2.4
9. Find an equation whose solution provides the answer to the
following problem. You need not solve the equation.
A corner lot has dimensions 35 by 40 yards. The city
plans to take a strip of uniform width along the two
sides of the lot that border the streets to widen these
roads. How wide should the strip be if the lot is to have
an area of 785 square yards?
10. A physics book has 40 square inches of print per page. Each
page has a left-side margin of 1.7 inches, and top, bottom, and
right-side margins of .4 inch. If a page cannot be wider than
7.4 inches, what should its dimensions be to use the least
amount of paper? Round your answer to three decimal places.
11. A radiator contains 8 quarts of fluid, 30% of which is an-
tifreeze. How much fluid should be drained and replaced
with pure antifreeze so that the new mixture is 40%
antifreeze? Round your answer to two decimal places.
12. Find the lowest point on the graph of y x
3
3x 3.1
shown in the given viewing windows.
(a) 0 x 3 and 3 y 3
(b) 2 x .99 and 3 y 6
13. The dimensions of a rectangular box are consecutive inte-
gers. If the box has volume 21,924 cubic centimeters, what
are its dimensions?
14. The population P of Cleveland, Ohio (in thousands) in year
x is approximated by
P .0000352x
4
.0049x
3
.08x
2
22.706x 375.2,
where x 0 corresponds to 1990. According to this model,
in what year was the population of Cleveland largest?
15. A rectangular bin with an open top and a volume of 42.32
cubic feet is to be built. The length of its base must be twice
the width, and the bin must be at least 3 feet high. Material
for the base of the bin costs $13 per square foot and material
for the sides costs $9 per square foot. If it coasts $634.34 to
build the bin, what are its dimensions?
16. A 10-inch square piece of metal is to be used to make an
open-top box by cutting equal-sized squares from each cor-
ner and folding up the sides. The length, width, and height
of the box are each to be less than 6 inches. Round your
answers to the following questions to three decimal places.
(a) If the box is to have a volume of 50 cubic inches, what
size squares should be cut from each corner?
(b) What size squares should be cut to produce a box with
the largest possible volume?
Section 2.5
17. The table shows the population of Nowhere, Missouri in
selected years.
Year Population
1950 930,568
1970 681,185
1980 528,162
1990 401,901
2000 354,474
2007 250,040
