Hungerford T.W., Shaw D.J. Contemporary Precalculus: A Graphing Approach
Подождите немного. Документ загружается.

NUMERICAL METHODS
In addition to graphical tools for solving equations, calculators and computer
algebra systems have equation solvers that can find or approximate the solutions
of most equations. On most calculators, the solver finds one solution at a time.
You must enter the equation and an initial guess and possibly an interval in which
to search. A few calculators (such as TI-89) and most computer systems have one-
step equation solvers that will find or approximate all the solutions in a single
step. Check you calculator instruction manual or your computer’s help menu for
directions on using these solvers.
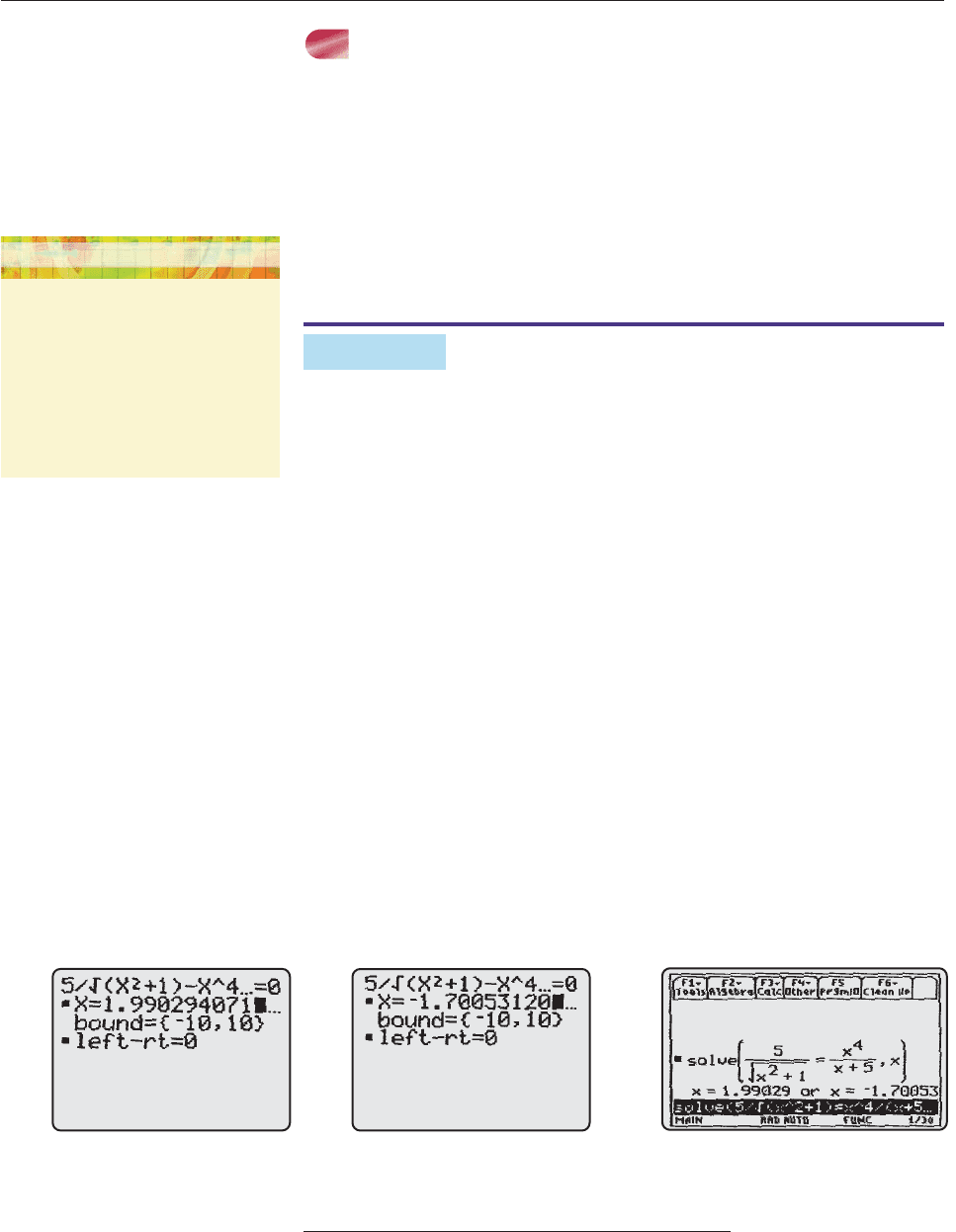
EXAMPLE 5
Use an equation solver to solve
x
x
4
5
.
SOLUTION On the TI-84 solver, the equation must be put in the form
x
x
4
5
0. When asked to find a solution in the interval 10 x 10,
with an initial guess of 1, the solver found the one in Figure 2–32. We changed the
initial guess to 1 to produce the solution in Figure 2–33.*
The one-step solver on a TI-89 produced both solutions of the equation
(Figure 2–34).
The first solution in Figure 2–34 was found on Maple with the command
fsolve(5/sqrt(x^2 1) x^4/(x 5) 0, x);
and the second was found by changing the search interval to 10 x 0, with
the command
fsolve(5/sqrt(x^2 1) x^4/(x 5) 0, x, x 10. . 0). ■
5
x
2
1
5
x
2
1
96 CHAPTER 2 Graphs and Technology
*In some cases, you may also have to change the search interval to find additional solutions.
Figure 2–33
Figure 2–32
Figure 2–34
TECHNOLOGY TIP
To call up the equation solver, use this
menu/choice:
TI-84: MATH/Solver
TI-86: SOLVER (keyboard)
TI-89: ALGEBRA/Solve
HP-39gs: APLET/Solve
Casio: EQUA (Main Menu)/Solver
Several calculators and many computer algebra systems also have polyno-
mial solvers, one-step solvers designed specifically for polynomial equations;
you need only enter the degree and coefficients of the polynomial. A few of
these (such as Casio 9850) are limited to equations of degree 2 and 3. Directions
for using polynomial solvers on calculators are in Exercise 105 on page 31.
Computer users should check the help menu for the proper syntax.
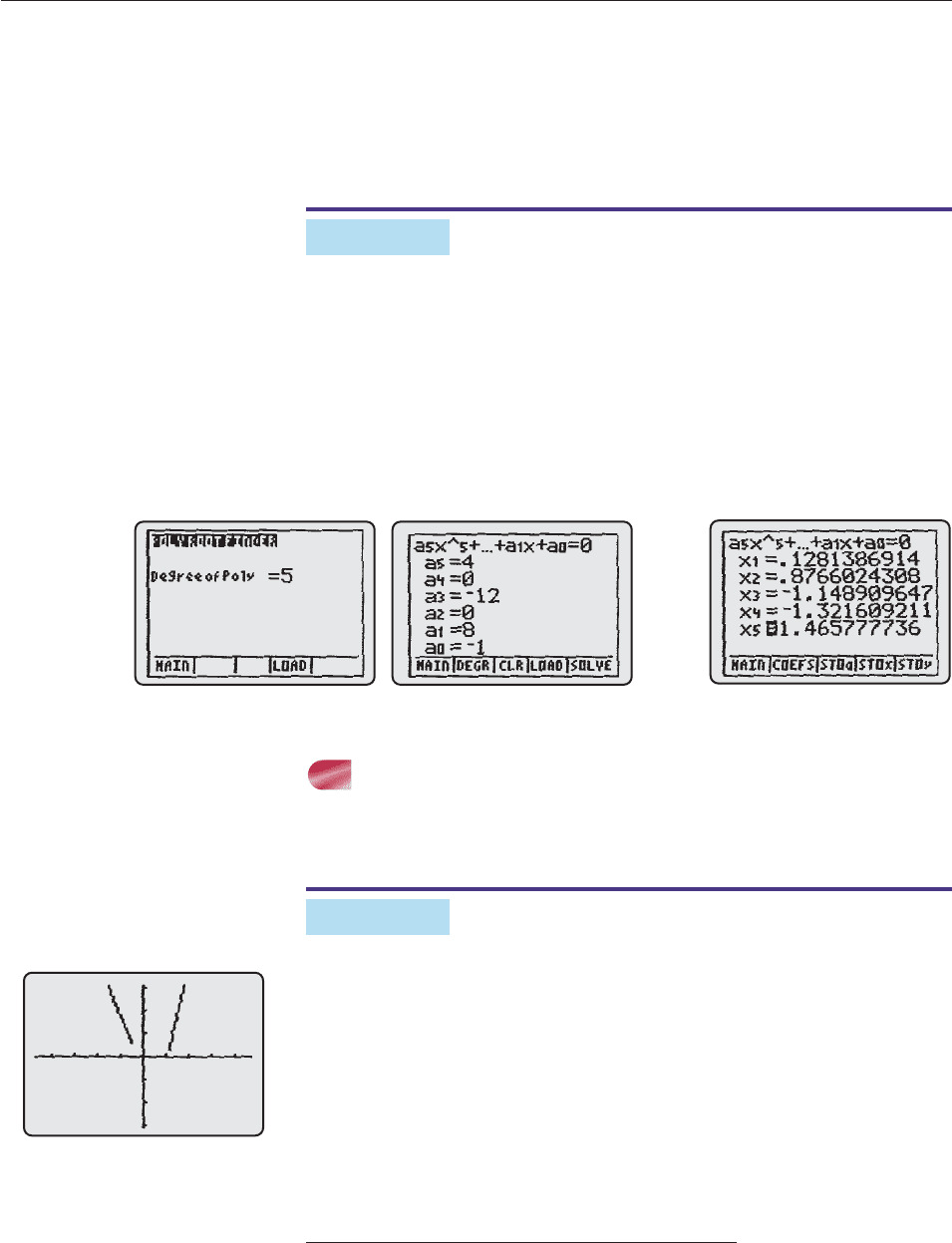
EXAMPLE 6
Use a polynomial solver to solve
4x
5
12x
3
8x 1 0.
SOLUTION We enter the degree and the coefficients of the equation in
the polynomial solver (Figure 2–35) and press SOLVE to obtain the five
solutions (Figure 2–36).* The fsolve command on Maple also produced all five
solutions. ■
SECTION 2.2 Solving Equations Graphically and Numerically 97
Figure 2–35
Figure 2–36
*This illustrates the procedure for TI-84 and 86. For HP-39gs, see Exercise 105 on page 31.
STRATEGIES FOR SPECIAL CASES
Because of various technological shortcomings, some equations are easier to
solve if an indirect approach is used.
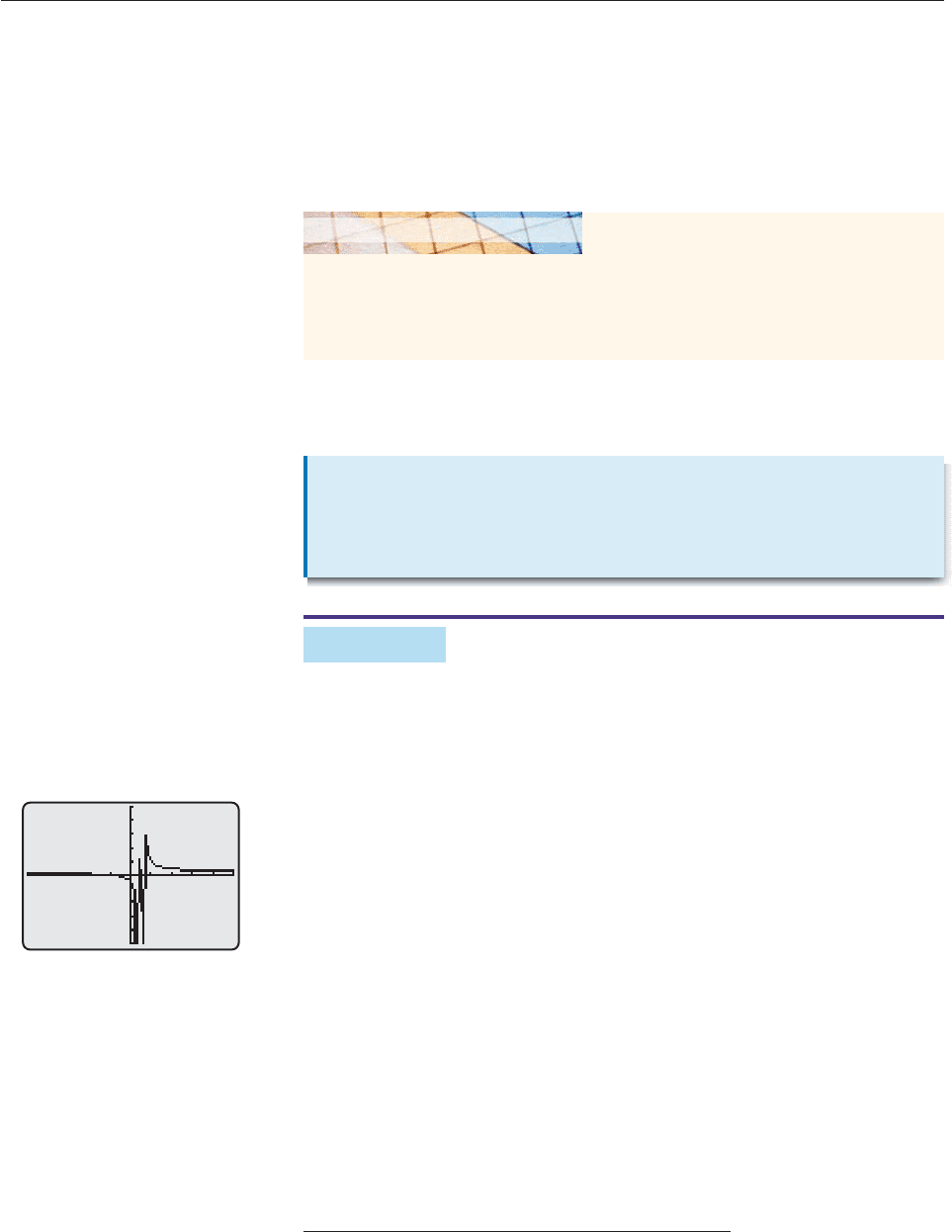
EXAMPLE 7
Solve x
4
x
2
2x
1
0.
SOLUTION The graph of y
x
4
x
2
2x
1
in Figure 2–37 does not
even appear to touch the x-axis (although it actually does touch at two places).
Consequently, some solvers and graphical root finders will return an error mes-
sage (check yours). Even if your root finder or solver can handle this equation, it
may fail in other similar situations. So the best approach is to use the following
fact:
The only number whose square root is 0 is 0 itself.
3.1
3.1
4.7 4.7
Figure 2–37
If you have a polynomial or one-step solver, use it to find all the real solutions of
x
4
x
2
2x 1 0 at once. Otherwise, graph y x
4
x
2
2x 1 and use the
graphical root finder to obtain the solutions one at a time. Verify that the real solutions
of this equation, and hence, of the original one, are x .4046978 and x 1.1841347.
■
GRAPHING EXPLORATION
Thus, x
4
x
2
2x
1
0 exactly when x
4
x
2
2x 1 0. So you need
only solve the polynomial equation
x
4
x
2
2x 1 0,
which is easily done on any calculator or computer. In fact, if you have a polyno-
mial or one-step solver, you can find all the solutions at once, which is faster than
solving the original equation with a root finder or other solvers.
98 CHAPTER 2 Graphs and Technology
The technique used in Example 7 is recommended for all similar situations.
Radical
Equations
To solve an equation of the form
Expres
sion in
x
0,
set the expression under the radical equal to 0 and solve the resulting equation.
EXAMPLE 8
Solve
9
2
x
x
2
2
9
x
x
1
2
0.
SOLUTION If you graph
y
9
2
x
x
2
2
9
x
x
1
2
,
you may get “garbage,” as in Figure 2–38. You could experiment with other view-
ing windows, but it’s easier to use this fact:
A fraction is 0 exactly when its numerator is 0 and
its denominator is nonzero.
To find where the numerator is 0, we need only solve 2x
2
x 1 0. This is
easily done algebraically.*
2x
2
x 1 0
(2x 1)(x 1) 0
x 1/2orx 1
You can readily verify that neither of these numbers make the denominator 0.
Hence, the solutions of the original equation are 1/2 and 1. ■
*In other cases, you may need technology to solve the numerator equation.
5
−5
−55
Figure 2–38

Example 8 illustrates a useful technique.
SECTION 2.2 Solving Equations Graphically and Numerically 99
Fractional
Equations
To solve an equation of the form
Fraction 0,
set the numerator equal to 0 and solve the resulting equation. The solutions
that do not make the denominator of the fraction 0 are the solutions of the
original equation.*
CHOOSING A SOLUTION METHOD
We have seen that equations can be solved by algebraic, graphical, and numerical
methods. Each method has both advantages and disadvantages, as summarized in
the table.
The choice of solution method is up to you. In the rest of this book, we nor-
mally use algebraic means for solving linear and quadratic equations because this
is often the fastest and most accurate method. Naturally, any such equation can
also be solved graphically or numerically (and you may want to do that as a check
against errors). Except in special cases, graphical and numerical methods will
normally be used for more complicated equations.
*A number that makes both numerator and denominator 0 is not a solution of the original equation
because 0/0 is not defined.
Solution Method Advantages Possible Disadvantages
Algebraic Produces exact solutions. May be difficult or impossible to
use with complicated equations.
Graphical Works well for a large Solutions may be
Root Finder or variety of equations. approximations.
Gives visual picture of Finding a useable viewing
the location of the window may take a
solutions. lot of time.
Numerical Solutions may be
Equation Solvers approximations.
Polynomial solver Fast and easy. Works only for polynomial
equations.
One-step solver Fast and easy. May miss some solutions or be
unable to solve certain equations.
Other solvers May require a considerable
amount of work to find the
particular solution you want.
Intersection Finder
Easiest method for most
linear and quadratic
equations.

100 CHAPTER 2 Graphs and Technology
EXERCISES 2.2
In Exercises 1–6, determine graphically the number of solu-
tions of the equation, but don’t solve the equation. You may
need a viewing window other than the standard one to find all
the x-intercepts.
1. x
5
5 3x
4
x
2. x
3
5 3x
2
24x
3. x
7
10x
5
15x 10 0
4. x
5
36x 25 13x
3
5. x
4
500x
2
8000x 16x
3
32,000
6. 6x
5
80x
3
45x
2
30 45x
4
86x
In Exercises 7–20, use graphical approximation (a root finder
or an intersection finder) to find a solution of the equation in
the given open interval.
7. x
3
4x
2
10x 15 0; (3, 2)
8. x
3
9 3x
2
6x; (1, 2)
9. x
4
x 3 0; (, 0)
10. x
5
5 3x
4
x; (2, )
11. x
4
x
3
x
3
0; (, 0)
12. 8x
4
14x
3
9x
2
11x
1
0; (, 0)
13.
2
5
x
5
x
2
2
x
0; (0, )
14. x
4
x
2
3x
1
0; (0, 1)
15. x
2
x 5
;(2, 1)
16. x
2
1
x 9
0; (3, 4)
17.
2
x
x
3
5
x
1
2
0
x
12x
5
0; (1, )
18. 0; (1, )
19.
x
x
3
2
4
x
x
6
1
0; (, 0)
20.
x
4
2
x
3
1
0; (0, ) [Hint: Write the left side as a
single fraction.]
In Exercises 21–34, use algebraic, graphical, or numerical
methods to find all real solutions of the equation, approximat-
ing when necessary.
21. 2x
3
4x
2
x 3 0
22. 6x
3
5x
2
3x 2 0
23. x
5
6x 6 0 24. x
3
3x
2
x 1 0
25. 10x
5
3x
2
x 6 0 26.
1
4
x
4
x 4 0
27. 2x
1
2
x
2
1
1
2
x
4
0
28.
1
4
x
4
1
3
x
2
3x 1 0
3x
5
15x 5
x
7
8x
5
2x
2
5
29.
x
2
5
x
1
2x 3 0 30.
x
2
x
5
1
31. x
2
4 3x
2
2x 1 32. x
3
2 5 x x
2
33. x
2
3
x 2
5
34. x
3
2
x 5
4
In Exercises 35–40, find an exact solution of the equation in
the given open interval. (For example, if the graphical approxi-
mation of a solution begins .3333, check to see whether 1/3 is
the exact solution. Similarly, 2
1.414; so if your approxi-
mation begins 1.414, check to see whether 2
is a solution.)
35. 3x
3
2x
2
3x 2 0; (0, 1)
36. 4x
3
3x
2
3x 7 0; (1, 2)
37. 12x
4
x
3
12x
2
25x 2 0; (0, 1)
38. 8x
5
7x
4
x
3
16x 2 0; (0, 1)
39. 4x
4
13x
2
3 0; (1, 2)
40. x
3
x
2
2x 2 0; (1, 2)
Exercises 41–46 deal with exponential, logarithmic, and
trigonometric equations, which will be dealt with in later chap-
ters. If you are familiar with these concepts, solve each equa-
tion graphically or numerically.
41. 10
x
1
4
x 28 42. e
x
6x 5
43. x sin
2
x
4 44. x
3
cos
3
x
5
45. 5 ln x x
3
x
2
5 46. ln x x
2
3 0
47. According to data from the U.S. Department of Education,
the average cost y of tuition and fees at four-year public col-
leges and universities in year x is approximated by
y
180,11
5x
2
2,863,8
51x
11,383
,876
where x 0 corresponds to 2000. If this model continues to
be accurate, in what year will tuition and fees reach $7000?
Round your answer to the nearest year.
48. Use the information in Example 4 to determine the year in
which the population of San Diego reached 1.1 million
people.
49. According to data from the U.S. Department of Health and
Human Services, the cumulative number y of AIDS cases
(in thousands) as of year x is approximated by
y .004x
3
1.367x
2
54.35x 569.72 (0 x 11),
where x 0 corresponds to 1995.
(a) When did the cumulative number of cases reach
944,000?
(b) If this model remains accurate after 2006, in what year
will the cumulative number of cases reach 1.1 million?

50. The enrollment in public high schools (in millions of stu-
dents) in year x is approximated by
y .000035606x
4
.0021x
3
.02714x
2
.12059x
14.2996 (0 x 35),
where x 0 corresponds to 1975.* During the current cen-
tury, when was enrollment 13.9 million students?
51. In Example 4 of Section 1.1 (page 9), a formula is given for
determining how far you can see from a given height. Sup-
pose you are on a cruise ship and that you can see the top of
a lighthouse 12 miles away. About how high above water
level are you?
52. According to the U.S. Centers for Medicare and Medicaid
Services, total medical expenditures (in billions of dollars)
in the United States in year x are expected to be given by
y .035x
4
1.01x
3
4.91x
2
126.94x 1309.6,
where x 0 corresponds to 2000. When will expenditures
be $2.6 trillion?
53. When is the population of China expected to reach 1.4 bil-
lion people? [Hint: The equation that estimates the popula-
tion of China is in Exercise 28 of Section 2.1 (page 89).]
54. (a) How many real solutions does the equation
.2x
5
2x
3
1.8x k 0
have when k 0?
(b) How many real solutions does it have when k 1?
(c) Is there a value of k for which the equation has just one
real solution?
(d) Is there a value of k for which the equation has no real
solutions?
SECTION 2.3 Applications of Equations 101
*Based on data from the National Center for Educational Statistics.
Setting up
Applied Problems
1. Read the problem carefully, and determine what is asked for.
2. Label the unknown quantities by letters (variables), and, if appropriate,
draw a picture of the situation.
3. Translate the verbal statements in the problem and the relationships be-
tween the known and unknown quantities into mathematical language.
4. Consolidate the mathematical information into an equation in one vari-
able that can be solved or an equation in two variables that can be
graphed to determine at least one of the unknown quantities.
Here are some examples of how these guidelines are applied.
EXAMPLE 1
Set up the following problem: The average of two real numbers is 41.125, and
their product is 1683. What are the numbers?
2.3 Applications of Equations
■ Set up applied problems.
■ Translate verbal statements into mathematical language.
■ Solve applied problems.
Actual problem situations are usually described verbally. To solve such problems,
you must interpret this verbal information and express it as an equivalent mathe-
matical problem. The following guidelines may be helpful.
Section Objectives

SOLUTION Read: We are asked for two numbers. Label: Call the numbers x
and y. Translate:
English Language Mathematical Language
Two numbers x and y
Their average is 41.125.
x
2
y
41.125
Their product is 1683. xy 1683
Consolidate: One technique to use when you have two unknowns is to express
one in terms of the other and use this to obtain an equation in one variable. In this
case, we can do that by solving the second equation for y:
xy 1683
y
16
x
83
and substituting the result in the first equation:
x
2
y
41.125
41.125
Multiply both sides by 2: x
16
x
83
82.25.
The solution of this equation is one of the numbers, and 1683/x is the other. ■
EXAMPLE 2
Set up the following problem: A rectangle is twice as long as it is wide. If it has an
area of 24.5 square inches, what are its dimensions?
SOLUTION Read: We are asked to find the length and width. Label: Let x de-
note the width and y the length, and draw a picture of the situation, as in Figure 2–39.
Translate: Use the fact that the area of a rectangle is length width.
English Language Mathematical Language
The width and length of the rectangle x and y
The length is twice the width. y 2x
The area is 24.5 square inches. xy 24.5
Consolidate: Substitute y 2x in the area equation:
xy 24.5
x(2x) 24.5.
So the equation to be solved is 2x
2
24.5. ■
x
16
x
83
2
102 CHAPTER 2 Graphs and Technology
x
y
Figure 2–39

EXAMPLE 3
Set up this problem: A rectangular box with a square base and no top is to
have a volume of 20,000 cubic centimeters. If the surface area of the box is
4000 square centimeters, what are its dimensions?
SOLUTION Read: We must find the length, width, and height of the box.
Label: Let x denote the length. Since the base is square, the length and width are
the same. Let h denote the height, as in Figure 2–40. Translate: Recall that the
volume of a box is given by the product length width height and that the sur-
face area is the sum of the area of the base and the area of the four sides of the box.
Then we have these translations:
English Language Mathematical Language
The length, width, and height x, x, and h
The volume is 20,000 cm
3
. x
2
h 20,000
The surface area is 4000 cm
2
. x
2
4xh 4000
Consolidate: We have two equations in two variables, so we solve the first equa-
tion for h
h
20
x
,0
2
00
and substitute this result in the second equation:
x
2
4x
20
x
,0
2
00
4000
x
2
80,
x
000
4000.
The solution of this last equation will provide the solution of the problem. ■
Once you are comfortable with the process for setting up problems, you can
often do much of it mentally. In the rest of this section, the setup process will be
simplified or shortened.
Setting up a problem is only half the job. You must then solve the equation
you have obtained. Whenever possible, linear and quadratic equations should be
solved algebraically, giving exact answers. Other equations may require graphical
or numerical methods to find approximate solutions. Finally, you must check your
answers in the original problem:
Interpret your answers in terms of the original problem.
Do they make sense? Do they satisfy the required conditions?
In particular, an equation may have several solutions, some of which might not
make sense in the context of the problem. For instance, distance can’t be negative,
the number of people in a room cannot be a proper fraction, etc.
SECTION 2.3 Applications of Equations 103
h
x
x
Figure 2–40

APPLICATIONS
We begin with some problems involving interest. Recall that 8% means .08 and
that “8% of 227” means “.08 times 227,” that is, .08(227) 18.16. The basic rule
of annual simple interest is
Interest rate amount.
EXAMPLE 4
A high-risk stock pays dividends at a rate of 12% per year, and a savings account
pays 6% interest per year. How much of a $9000 investment should be put in the
stock and how much in the savings account to obtain a return of 8% per year on
the total investment?
SOLUTION Label: Let x be the amount invested in stock. Then the rest of the
$9000, namely, (9000 x) dollars, goes in the savings account. Translate: We
want the total return on $9000 to be 8%, so we have
Return on x dollars Return on (9000 x)
8% of $9000
of stock at 12% dollars of savings at 6%
(12% of x dollars) [6% of (9000 x) dollars] 8% of $9000
.12x .06(9000 x) .08(9000)
.12x .06(9000) .06x .08(9000)
.12x 540 .06x 720
.12x .06x 720 540
.06x 180
x
1
.0
8
6
0
3000.
Therefore, $3000 should be invested in stock and (9000 3000) $6000 in
the savings account. If this is done, the total return will be 12% of $3000
($360) plus 6% of $6000 ($360), a total of $720, which is precisely 8% of
$9000. ■
EXAMPLE 5
A car radiator contains 12 quarts of fluid, 20% of which is antifreeze. How much
fluid should be drained and replaced with pure antifreeze in order that the result-
ing mixture be 50% antifreeze?
104 CHAPTER 2 Graphs and Technology
—
—
—
————
———
20% of (12 x) x 50% of 12
.20(12 x) x .50(12)
2.4 .2x x 6
.2x x 6 2.4
.8x 3.6
x
3
.
.
8
6
4.5.
Therefore, 4.5 quarts should be drained and replaced with pure antifreeze. ■
The two preceding examples used only algebraic models (equations in one
variable). Sometimes a diagram (geometrical model) is helpful in visualizing the
situation and setting up an appropriate equation.
EXAMPLE 6
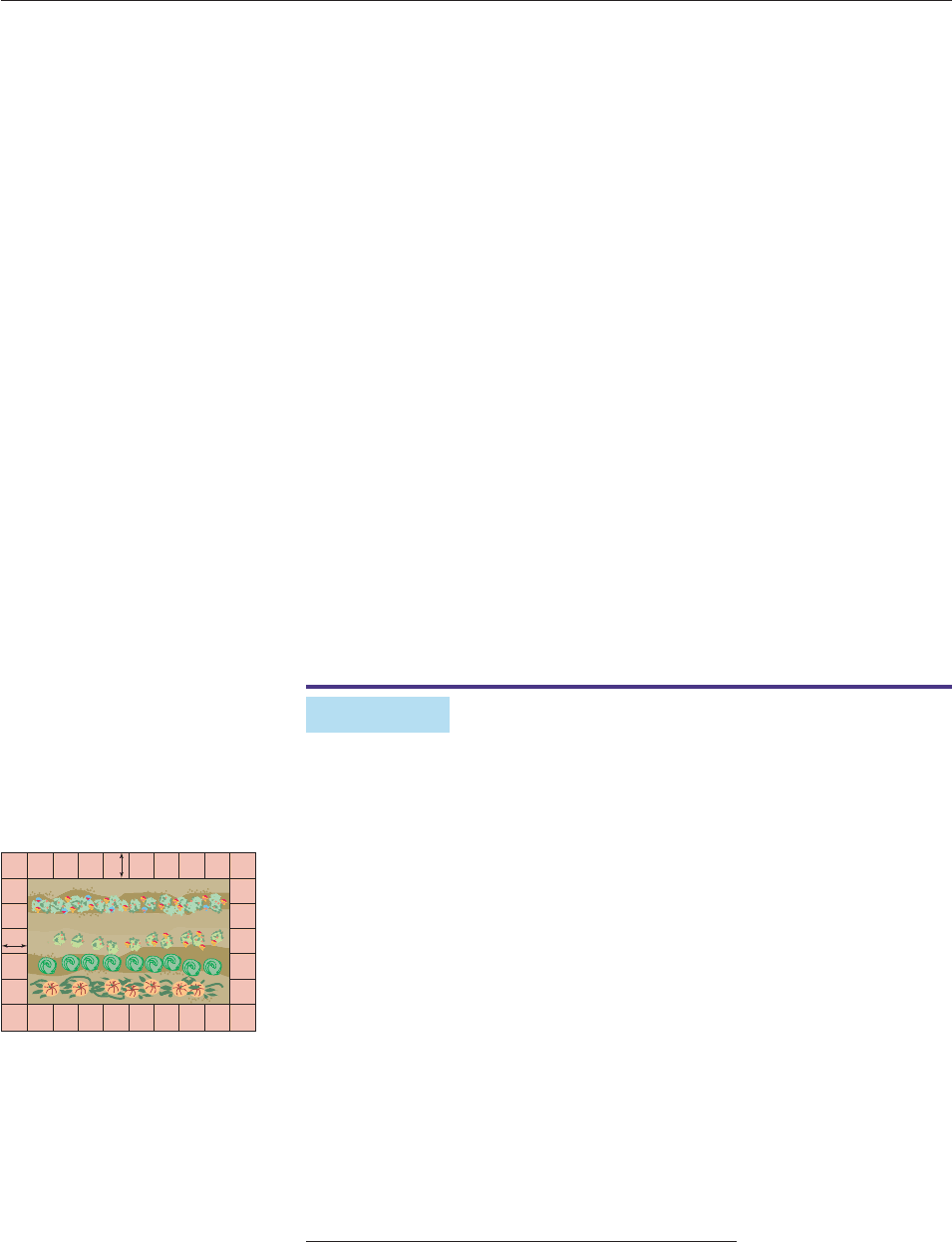
A landscaper wants to put a cement walk of uniform width around a rectangular
garden that measures 24 by 40 feet. She has enough cement to cover 660 square
feet. How wide should the walk be to use all the cement?
SOLUTION Let x denote the width of the walk (in feet), and draw a picture of
the situation (Figure 2–41).
The length of the outer rectangle is 40 2x (the garden length plus walks on
each end), and its width is 24 2x.
Area of outer Area of
Area of walk
rectangle garden
Length
Width Length
Width 660
(40 2x)(24 2x) 40
24 660
960 128x 4x
2
960 660
4x
2
128x 660 0.
SECTION 2.3 Applications of Equations 105
Amount of
antifreeze in
radiator after
draining x quarts
of fluid
x quarts of
antifreeze
Amount of
antifreeze in
final mixture
*Hereafter, we omit the headings Label, Translate, etc.
x
x
24
40
Figure 2–41
———
———
———
———
—————
—————
—
—
—
—
—
——
SOLUTION Let x be the number of quarts of fluid to be replaced by pure
antifreeze.* When x quarts are drained, there are 12 x quarts of fluid left in the
radiator, 20% of which is antifreeze. So we have
