Hungerford T.W., Shaw D.J. Contemporary Precalculus: A Graphing Approach
Подождите немного. Документ загружается.

61. x-intercept 5 and y-intercept 5.
62. Through (5, 2) and parallel to the line through (1, 2) and
(4, 3).
63. Through (1, 3) and perpendicular to the line through (0, 1)
and (2, 3).
64. y-intercept 3 and perpendicular to 2x y 6 0.
65. Find a real number k such that (3, 2) is on the line
kx 2y 7 0.
66. Find a real number k such that the line 3x ky 2 0 has
y-intercept 3.
If P is a point on a circle with center C, then the tangent line to
the circle at P is the straight line through P that is perpendicu-
lar to the radius CP. In Exercises 67–70, find the equation of
the tangent line to the circle at the given point.
67. x
2
y
2
25 at (3, 4) [Hint: Here C is (0, 0) and P is
(3, 4); what is the slope of radius CP?]
68. x
2
y
2
169 at (5, 12)
69. (x 1)
2
(y 3)
2
5 at (2, 5)
70. x
2
y
2
6x 8y 15 0 at (2, 1)
71. Let A, B, C, D be nonzero real numbers. Show that the lines
Ax By C 0 and Ax By D 0 are parallel.
72. Let L be a line that is neither vertical nor horizontal and
that does not pass through the origin. Show that L is the
graph of
a
x
b
y
1, where a is the x-intercept and b is the
y-intercept of L.
73. Worldwide motor vehicle production was about 60 million
in 2000 and about 66 million in 2005.
(a) Let the x-axis denote time and the y-axis the number of
vehicles (in millions). Let x 0 correspond to 2000.
Fill in the blanks: the given data is represented by the
points (___, 60) and (5, ___).
(b) Find the linear equation determined by the two points in
part (a).
(c) Use the equation in part (b) to estimate the number of
vehicles produced in 2004.
(d) If this model remains accurate, when will vehicle pro-
duction reach 72 million?
74. Carbon dioxide (CO
2
) concentration is measured regularly
at the Mauna Loa observatory in Hawaii. The mean annual
concentration in parts per million in various years is given
in the table.*
66 CHAPTER 1 Basics
(a) Let x 0 correspond to 1980. List the five data points
given by the table. Do these points all lie on a single
line? How can you tell?
(b) Use the data points from 1984 and 2004 to write a linear
equation to model CO
2
concentration over time.
(c) Do part (b), using the data points from 1994 and 2004.
(d) Use the two models to estimate the CO
2
concentration
in 1989 and 1999. Do the models overestimate or un-
derestimate the concentration?
(e) What do the two models say about the concentration in
2008? Which model do you think is the more accurate?
Why?
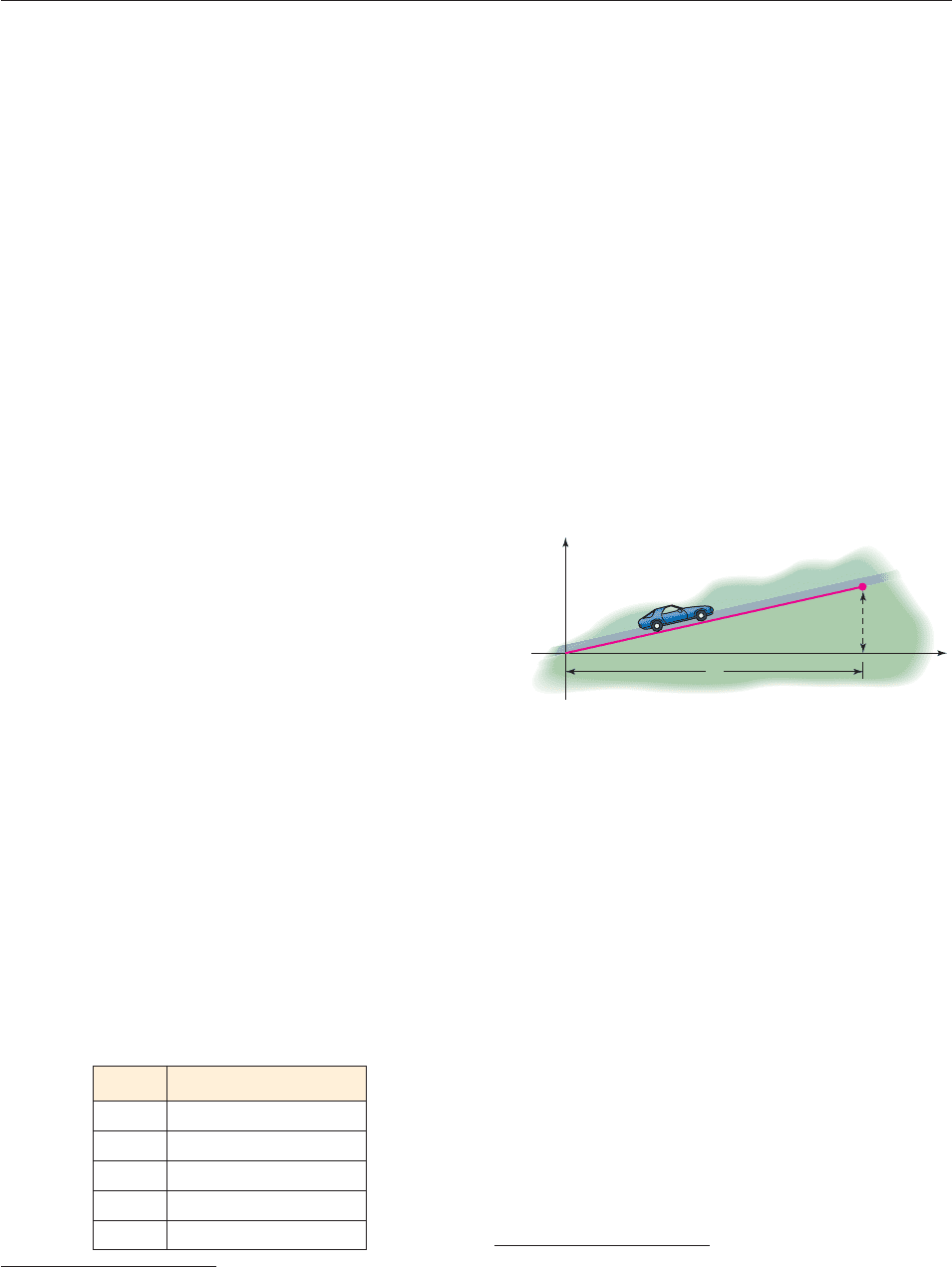
75. Suppose you drive along the Ohio Turnpike in an area
where the grade of the road is 3% (which means that the line
representing the road in the figure has slope .03.)
(a) Find the equation of the line representing the road.
[Hint: Your trip begins at the origin.]
(b) If you drive on the road for one mile, how many feet
higher are you at the end of the mile than you were at
the beginning? [Hint: Express one mile as 5280 feet.
Use the equation from part (a) to express x in terms of
y, and then use the Pythagorean Theorem to find y.]
76. The Missouri American Water Company charges residents
of St. Louis County $6.15 per month plus $2.0337 per thou-
sand gallons used.*
(a) Find the monthly bill when 3000 gallons of water are
used. What is the bill when no water is used?
(b) Write a linear equation that gives the monthly bill y
when x thousand gallons are used.
(c) If the monthly bill is $22.42, how much water was used?
77. At sea level, water boils at 212°F. At a height of 1100 feet,
water boils at 210°F. The relationship between boiling point
and height is linear.
(a) Find an equation that gives the boiling point y of water
at a height of x feet.
Find the boiling point of water in each of the following
cities (whose altitudes are given).
(b) Cincinnati, OH (550 feet)
(c) Springfield, MO (1300 feet)
(d) Billings, MT (3120 feet)
(e) Flagstaff, AZ (6900 feet)
78. According to the Center of Science in the Public Interest,
the maximum healthy weight for a person who is 5 feet
5 inches tall is 150 pounds, and the maximum healthy
x
x
y
y
Year Concentration (ppm)
1984 344.4
1989 352.9
1994 358.9
1999 368.3
2004 377.4
*Residential rates for a 58 inch meter in March 2006, assuming monthly
billing and maximum usage of 16,000 gallons.
*C. D. Keeling and T. P. Whorf, Scripps Institution of Oceanography
weight for someone 6 feet 3 inches tall is 200 pounds. The
relationship between weight and height here is linear.
(a) Find a linear equation that gives the maximum healthy
weight y for a person whose height is x inches over
4 feet 10 inches. (Thus x 0 corresponds to 4 feet
10 inches, x 2 to 5 feet, etc.)
(b) What is the maximum healthy weight for a person whose
height is 5 feet? 6 feet?
(c) How tall is a person who is at a maximum healthy
weight of 220 pounds?
79. The number of unmarried couples in the United States who
live together was 3.2 million in 1990 and grew in a linear
fashion to 5.5 million in 2000.*
(a) Let x 0 correspond to 1990. Write a linear equation
expressing the number y of unmarried couples living
together (in millions) in year x.
(b) Assuming the equation remains accurate, estimate the
number of unmarried couples living together in 2010.
(c) When will the number of unmarried couples living
together reach 10,100,000?
80. The percentage of people 25 years old and older who have a
Bachelor’s degree or higher was about 25.6 in 2000 and
27.7 in 2004.*
(a) Find a linear equation that gives the percentage of people
25 and over who have a Bachelor’s degree or higher in
terms of time t, where t is the number of years since 2000.
Assume that this equations remains valid in the future.
(b) What will the percentage be in 2010?
(c) When will 34% of those 25 and over have a Bachelor’s
degree or higher?
81. At the Factory in Example 14, the cost of producing x can
openers is given by y 2.75x 26,000.
(a) Write an equation that gives the average cost per can
opener when x can openers are produced.
(b) How many can openers should be made to have an
average cost of $3 per can opener?
82. Suppose the cost of making x TV sets is given by
y 145x 120,000.
(a) Write an equation that gives the average cost per set
when x sets are made.
(b) How many sets should be made in order to have an
average cost per set of $175?
83. The profit p (in thousands of dollars) on x thousand units of
a specialty item is p .6x 14.5. The cost c of manufac-
turing x thousand items is given by c .8x 14.5.
(a) Find an equation that gives the revenue r from selling
x thousand items.
(b) How many items must be sold for the company to break
even (i.e., for revenue to equal cost)?
84. A publisher has fixed costs of $110,000 for a mathematics
text. The variable costs are $50 per book. The book sells for
$72. Find equations that give
SECTION 1.4 Lines 67
(a) The cost c of making x books
(b) The revenue r from selling x books
(c) The profit p from selling x books
(d) What is the publisher’s break-even point (see Exer-
cise 83(b))?
Use the graph and the following information for Exer-
cises 85–86. Rocky is an “independent” ticket dealer who
markets choice tickets for Los Angeles Lakers home games.
(California currently has no laws against ticket scalping.) Each
graph shows how many tickets will be demanded by buyers at a
particular price. For instance, when the Lakers play the
Chicago Bulls, the graph shows that at a price of $160, no
tickets are demanded. As the price (y-coordinate) gets lower,
the number of tickets demanded (x-coordinate) increases.
85. Write a linear equation that relates the quantity x of tickets
demanded at price y when the Lakers play the
(a) Dallas Mavericks (b) Phoenix Suns
(c) Chicago Bulls
[Hint: In each case, use the x- and y-intercepts to determine
its slope.]
86. Use the equations from Exercise 85 to find the number of tick-
ets Rocky would sell at a price of $40 for a game against the
(a) Mavericks (b) Bulls
87. The Fahrenheit and Celsius scales for measuring tempera-
tures are linearly related. They are calibrated using the
freezing and boiling points of water at sea level.
20
0
40
60
80
100
120
140
160
20
Bulls
Suns
Mavericks
Quantity
30 4010
Price
x
y
*U.S. Census Bureau
Temperature Fahrenheit Celsius
Scale Scale Scale
Water Freezes 32° 0°
Water Boils 212° 100°
(a) Use the data in the table to write a formula that relates
the Fahrenheit temperature F to the Celsius tempera-
ture C. Your answer should be in the form F mC b.
(b) Solve the equation in part (a) for C to find a formula
that relates the Celsius temperature to the Fahrenheit
temperature.
(c) When is the temperature in degrees Fahrenheit the same
as the temperature in degrees Celsius?
88. (a) If the temperature changes 1° Fahrenheit, how many
degrees does the Celsius temperature change? [Hint:
See Exercise 87.]

(b) What happens to the Fahrenheit temperature when the
Celsius temperature changes 1°?
(c) How are your answers in parts (a) and (b) related to the
formulas in Exercises 87?
89. A 75-gallon water tank is being emptied. The graph shows
the amount of water in the tank after x minutes.
(a) At what rate is the tank emptying during the first 2 min-
utes? During the next 3 minutes? During the last minute?
(b) Suppose the tank is emptied at a constant rate of 10 gal-
lons per minute. Draw the graph that shows the amount of
water after x minutes. What is the equation of the graph?
90. The poverty level income for a family of four was $13,359
in 1990. Because of inflation and other factors, the poverty
level rose approximately linearly to $19,307 in 2004.*
(a) At what rate is the poverty level increasing?
(b) Estimate the poverty level in 2000 and 2009.
91. A Honda Civic LX sedan is worth $15,350 now and will be
worth $9910 in four years.
(a) Assuming linear depreciation, find the equation that
gives the value y of the car in year x.
(b) At what rate is the car depreciating?
(c) Estimate the value of the car six years from now.
92. A house in Shaker Heights, Ohio was bought for $160,000
in 1980. It increased in value in an approximately linear
fashion and sold for $359,750 in 1997.
(a) At what rate did the house appreciate (increase in
value) during this period?
(b) If this appreciation rate remained accurate what would
the house be worth in 2010?
THINKERS
93. Show that two nonvertical lines with the same slope
are parallel. [Hint: The equations of distinct lines with
the same slope must be of the form y mx b and
y mx c with b c (why?). If (x
1
, y
1
) were a point on
both lines, its coordinates would satisfy both equations.
Show that this leads to a contradiction, and conclude that
the lines have no point in common.]
94. Prove that nonvertical parallel lines L and M have the same
slope, as follows. Suppose M lies above L, and choose two
points (x
1
, y
1
) and (x
2
, y
2
) on L.
75
50
25
204
Minutes
Gallons
6
0
y
x
68 CHAPTER 1 Basics
(a) Let P be the point on M with first coordinate x
1
. Let b
denote the vertical distance from P to (x
1
, y
1
). Show that
the second coordinate of P is y
1
b.
(b) Let Q be the point on M with first coordinate x
2
. Use the
fact that L and M are parallel to show that the second
coordinate of Q is y
2
b.
(c) Compute the slope of L using (x
1
, y
1
) and (x
2
, y
2
). Com-
pute the slope of M using the points P and Q. Verify that
the two slopes are the same.
95. Show that the diagonals of a square are perpendicular.
[Hint: Place the square in the first quadrant of the plane,
with one vertex at the origin and sides on the positive axes.
Label the coordinates of the vertices appropriately.]
96. This exercise provides a proof of the statement about slopes
of perpendicular lines in the box on page 61. First, assume
that L and M are nonvertical perpendicular lines that both
pass through the origin. L and M intersect the vertical line
x 1 at the points (1, k) and (1, m), respectively, as shown
in the figure.
(a) Use (0, 0) and (1, k) to show that L has slope k. Use
(0, 0) and (1, m) to show that M has slope m.
(b) Use the distance formula to compute the length of each
side of the right triangle with vertices (0, 0), (1, k),
and (1, m).
(c) Use part (b) and the Pythagorean Theorem to find an
equation involving k, m, and various constants. Show
that this equation simplifies to km 1. This proves
half of the statement.
(d) To prove the other half, assume that km 1, and
show that L and M are perpendicular as follows. You
may assume that a triangle whose sides a, b, c satisfy
a
2
b
2
c
2
is a right triangle with hypotenuse c. Use
this fact, and do the computation in part (b) in reverse
(starting with km 1) to show that the triangle with
vertices (0, 0), (1, k), and (1, m) is a right triangle, so
that L and M are perpendicular.
(e) Finally, to prove the general case when L and M do not
intersect at the origin, let L
1
be a line through the origin
that is parallel to L, and let M
1
be a line through the ori-
gin that is parallel to M. Then L and L
1
have the same
slope, and M and M
1
have the same slope (why?). Use
this fact and parts (a)–(d) to prove that L is perpendicu-
lar to M exactly when km 1.
1
(1, m)
(1, k)
M
L
*U.S. Census Bureau

CHAPTER 1 Review 69
Chapter 1 Review
IMPORTANT CONCEPTS
Section 1.1
Real numbers, integers, rationals,
irrationals 2–3
Order of operations 3
Distributive law 4
Number line 4
Order (, , , ) 4–5
Intervals, open intervals, closed
intervals 5
Negatives 6
Scientific notation 7
Square roots 8
Absolute value 9
Distance on the number line 11
Special Topics 1.1.A
Repeating and nonrepeating
decimals 17
Section 1.2
Basic principles for solving
equations 19
First-degree equations 19–20
Quadratic equations 20
Factoring 20–21
Completing the square 22
Quadratic formula 23
Discriminant 24
Higher-degree equations 26
Fractional equations 27
Special Topics 1.2.A
Absolute value equations 32
Special Topics 1.2.B
Direct variation 34
Inverse variation 34
Constant of variation 34
Section 1.3
Coordinate plane, x-axis, y-axis,
quadrants 39–40
Scatter plots and line graphs 41
Distance formula 41
Midpoint formula 43
Graph of an equation 44
x- and y-intercepts 44–45
Circle, center, radius 46
Equation of the circle 46
Unit circle 48
Section 1.4
Change in x, change in y 54
Slope 54
Properties of slope 56
Slope-intercept form of the equation
of a line 57
Horizontal lines 58
Vertical lines 58
Point-slope form of the equation
of a line 58
General form of the equation
of a line 60
Slopes of parallel lines 60
Slopes of perpendicular lines 61
Fixed and variable costs 63
Linear rate of change 64
IMPORTANT FACTS & FORMULAS
■
c d distance from c to d on the number line.
■
Quadratic Formula: If a 0, then the solutions of ax
2
bx c 0 are
x
b
2a
b
2
4
ac
.
■
If a 0, then the number of real solutions of ax
2
bx c 0 is 0, 1, or 2, depending on whether the
discriminant b
2
4ac is negative, zero, or positive.
■
Distance Formula: The distance from (x
1
, y
1
) to (x
2
, y
2
) is
(x
1
x
2
)
2
(
y
1
y
2
)
2
.
■
Midpoint Formula: The midpoint of the line segment from (x
1
, y
1
) to (x
2
, y
2
) is
x
1
2
x
2
,
y
1
2
y
2
.
■
Equation of the circle with center (c, d) and radius r is
(x c)
2
( y d)
2
r
2
.

70 CHAPTER 1 Basics
■
The slope of the line through (x
1
, y
1
) and (x
2
, y
2
) (where x
1
x
2
) is
y
x
2
2
y
x
1
1
.
■
The equation of the line with slope m and y-intercept b is
y mx b.
■
The equation of the line through (x
1
, y
1
) with slope m is
y y
1
m(x x
1
).
■
Two nonvertical lines are parallel exactly when they have the same slope.
■
Two nonvertical lines are perpendicular exactly when the product of their slopes is 1.
1. Fill the blanks with one of the symbols , , or so that
the resulting statement is true.
(a) 142 51 (b) 2
2
(c) 1000
1
1
0
(d) 2 6
(e) u vv u, where u and v are fixed real num-
bers.
2. List two real numbers that are not rational numbers.
3. Express in symbols:
(a) y is negative, but greater than 10.
(b) x is nonnegative and not greater than 10.
4. Express in symbols:
(a) c 7 is nonnegative.
(b) .6 is greater than 5x 2.
5. Express in interval notation:
(a) The set of all real numbers that are strictly greater than
8;
(b) The set of all real numbers that are less than or equal to 5.
6. Express in interval notation:
(a) The set of all real numbers that are strictly between 6
and 9;
(b) The set of all real numbers that are greater than or equal
to 5, but strictly less than 14.
7. Express in scientific notation:
(a) 12,320,000,000,000,000 (b) .0000000000789
8. Express in decimal notation:
(a) 4.78 10
8
(b) 6.53 10
9
9. Express in symbols:
(a) x is less than 3 units from 7 on the number line.
(b) y is farther from 0 than x is from 3 on the number line.
10. Simplify: b
2
2b 1 11. Solve: x 5 3
12. Solve: x 2 4
13. Solve: x 3
5
2
14. Solve: x 5 2 15. Solve: x 2 2
16. When John-Paul carves pumpkins, he will not use any that
weigh less than 2 pounds or more than 10 pounds. If x
represents the weight of a pumpkin in pounds that he will
not use, which of the following statements is always true?
(a) x 2 10
(b) x 4 6
(c) x 5 5
(d) x 6 4
(e) x 10 4
17. (a) p 7 (b) 23 3
18. If c and d are real numbers with c d what are the
possible values of
c
c
d
d
?
19. Express .282828 as a fraction.
20. Express .362362362 as a fraction.
21. Solve for x:
2
5
x
7
3x
x
5
2
4.
22. Solve for x in terms of y: xy 3 x 2y
23. Solve for x:3x
2
2x 5 0
24. Solve for y:3y
2
2y 5
25. Solve for z:5z
2
6z 7
26. The population P (in thousands) of St. Louis, Missouri, can
be approximated by
P .11x
2
15.95x 864,
where x 0 corresponds to 1950. When did the popula-
tion first drop below 450,000?
27. How many times larger is the viewing area on a 21-inch
computer monitor than on a 14-inch monitor? Remember
REVIEW QUESTIONS

that the size of a monitor is its diagonal measurement, as
shown in the figure, and assume that the height of the screen
is three-fourths of its width.
28. The median sales price S (in thousands of dollars) for a
single-family home in the midwestern United States can be
approximated by S .1x
2
3.9x 74.5, where x 0 cor-
responds to 1990.* When did the median price reach
$136,000?
29. Find the number of real solutions of the equation
20x
2
12 31x.
30. For what value of k does the equation
kt
2
5t 2 0
have exactly one real solution for t?
31. Solve for x:
3
x
x
5
2
2.
32. Solve for z: 2
z
1
2
z
z
3
2
.
33. If x and y are directly proportional and x 12 when y 36,
then what is y when x 2?
34. Driving time varies inversely as speed. If it takes 3 hours
to drive to the beach at an average speed of 48 mph, how
long will it take to drive home at an average speed of 54
mph?
35. Find the constant of variation when T varies directly as the
square of R and inversely as S if T .6 when R 3 and
S 15.
36. The statement “r varies directly as s and the square root
of t and inversely as the cube of x” means that for some con-
stant k,
(a) r kstx
3
(b) rx
3
ks t
(c) r
kx
3
s
t
(d) k
rs
x
3
t
(e) kx
3
s k t
In Questions 37–40, find all real solutions of the equation. Do
not approximate.
37. x
4
11x
2
18 0 38. x
6
4x
3
4 0
39. 3x 1 4 40. 2x 1 x 4
21 in.
x
CHAPTER 1 Review 71
41. Find the distance from (1, 2) to (4, 5).
42. Find the distance from (3/2, 4) to (3, 5/2).
43. Find the distance from (c, d) to (c d, c d ).
44. Find the midpoint of the line segment from (4, 7) to
(9, 5).
45. Find the midpoint of the line segment from (c, d ) to
(2d c, c d ).
46. Find the equation of the circle with center (3, 4) that
passes through the origin.
47. (a) If (1, 1) is on a circle with center (2, 3), what is the ra-
dius of the circle?
(b) Find the equation of the circle in part (a).
48. Sketch the graph of 3x
2
3y
2
12.
49. Sketch the graph of (x 5)
2
y
2
9 0.
50. Find the center and radius of the circle whose equation is
x
2
y
2
2x 6y 1 0.
51. Which of statements (a)–(d) are descriptions of the circle
with center (0, 2) and radius 5?
(a) The set of all points (x, y) that satisfy
x y 2 5.
(b) The set of all points whose distance from (0, 2) is 5.
(c) The set of all points (x, y) such that
x
2
(y 2)
2
5.
(d) The set of all points (x, y) such that
x
2
(y
2)
5
5.
52. If the equation of a circle is 3x
2
3(y 2)
2
12, which of
the following statements is true?
(a) The circle has diameter 3.
(b) The center of the circle is (2, 0).
(c) The point (0, 0) is on the circle.
(d) The circle has radius 12.
(e) The point (1, 1) is on the circle.
53. The graph of one of the equations below is not a circle.
Which one?
(a) x
2
(y 5)
2
p
(b) 7x
2
4y
2
14x 3y
2
2 0
(c) 3x
2
6x 3 3y
2
15
(d) 2(x 1)
2
8 2(y 3)
2
(e)
x
4
2
y
4
2
1
54. The point (7, 2) is on the circle whose center is on the
midpoint of the segment joining (3, 5) and (5, 1). Find
the equation of this circle.
55. The table on the next page shows fatal crash involvements
per 100 million miles traveled by drivers of selected ages.*
Sketch a scatter plot and a line graph for this data.
*Department of Housing and Urban Development
*Insurance Institute for Highway Safety

72 CHAPTER 1 Basics
56. The table shows the average speed (mph) of the winning car
in the Indianapolis 500 race in selected years.* Sketch a
scatter plot and a line graph for this data, letting x 0 cor-
respond to 1992.
57. (a) What is the y-intercept of the graph of the line
y x
x
5
2
3
5
?
(b) What is the slope of the line?
58. Find the equation of the line passing through (1, 3) and
(2, 5).
59. Find the equation of the line passing through (2, 1) with
slope 3.
60. Find all points on the graph of y 3x whose distance to the
origin is 2.
61. Find the equation of the line that crosses the y-axis at y 1
and is perpendicular to the line 2y x 5.
62. (a) Find the y-intercept of the line 2x 3y 4 0.
(b) Find the equation of the line through (1, 3) that has the
same y-intercept as the line in part (a).
63. Find the equation of the line through (4, 5) that is parallel
to the line through (1, 3) and (4, 2).
64. Sketch the graph of the line 3x y 1 0.
65. As a balloon is launched from the ground, the wind is blow-
ing it due east. The conditions are such that the balloon is
ascending along a straight line with slope 1/5. After 1 hour
the balloon is 5000 feet vertically above the ground. How
far east has the balloon blown?
66. The point (u, v) lies on the line y 5x 10. What is the
slope of the line passing through (u, v) and the point
(0, 10)?
In Questions 67–73, determine whether the statement is true or
false.
67. The graph of x 5y 6 has y-intercept 6.
68. The graph of 2y 8 3x has y-intercept 4.
69. The lines 3x 4y 12 and 4x 3y 12 are perpendicular.
70. Slope is not defined for horizontal lines.
71. The line in the figure has positive slope.
72. The line in the figure above does not pass through the third
quadrant.
73. The y-intercept of the line in the figure above is negative.
74. Consider the slopes of the lines shown in the figure below.
Which line has the slope with the largest absolute value?
75. Which of the following lines rises most steeply from left to
right?
(a) y 4x 10 (b) y 3x 4
(c) 20x 2y 20 0 (d) 4x y 1
(e) 4x 1 y
76. Which of the following lines is not perpendicular to the line
y x 5?
(a) y 4 x (b) y x 5
(c) 4 2x 2y 0 (d) x 1 y
(e) y x
1
5
77. Which of the following does not pass through the third
quadrant?
(a) y x (b) y 4x 7
(c) y 2x 5 (d) y 4x 7
(e) y 2x 5
78. Let a, b be fixed real numbers. Where do the lines x a and
y b intersect?
(a) Only at (b, a). (b) Only at (a, b).
(c) These lines are parallel, so they don’t intersect.
(d) If a b, then these are the same line, so they have infi-
nitely many points of intersection.
(e) Since these equations are not of the form y mx b,
the graphs are not lines.
D
E
C
B
A
y
x
y
x
1
1
−1
−1
Year 1992 1994 1996 1998 2000 2002 2004
Speed 134 161 148 145 168 166 139
Age of Driver 16 17 18 19 23 28 33
Fatal crashes 9.3 8.3 6.5 7.2 4.3 2.3 1.6
*Indianapolis Motor Speedway Hall of Fame and Museum
CHAPTER 1 Test 73
79. Which of the following is an equation of a line with y-inter-
cept 2 and x-intercept 3?
(a) 2x 3y 6 (b) 2x 3y 4
(c) 2x 3y 6 (d) 2x 3y 4
(e) 3x 2y 6
80. For what values of k will the graphs of 2y x 3 0 and
3y kx 2 0 be perpendicular lines?
81. Average life expectancy increased linearly from 74.7 years
for a person born in 1985 to 77.8 years for a person born
in 2005.
(a) Find a linear equation that gives the average life
expectancy y of a person born in year x, with
x 0 corresponding to 1985.
(b) Use the equation in part (a) to estimate the average life
expectancy of a person born in 1990.
(c) Assuming the equation remains valid, in what year will
the average life expectancy be 80 years for people born
in that year?
82. The population of San Diego, California, grew in an ap-
proximately linear fashion from 1,110,600 in 1990 to
1,263,700 in 2004.
(a) Find a linear equation that gives the population
y of San Diego (in thousands) in year x, with x 0
corresponding to 1990.
(b) Estimate the population of San Diego in 2010.
(c) Assuming the equation remains accurate, when will San
Diego’s population reach 1.5 million people?
In Exercises 83–86, match the given information with one of
the graphs (a)–(d), and determine the slope of the graph.
y
100
200
300
36
(a)
912
x
83. A salesman is paid $300 per week plus $75 for each unit
sold.
84. A person is paying $25 per week to repay a $300 loan.
85. A gold coin that was purchased for $300 appreciates
$20 per year.
86. A CD player that was purchased for $300 depreciates
$80 per year.
y
200
400
600
24
(d)
68
x
y
1000
800
600
400
200
(c)
12108642
x
y
100
200
300
12
(b)
34
x
Sections 1.1 and 1.2; Special Topics 1.1.A
and 1.2.A.
1. (a) Draw a picture on the number line of the interval [3, 2).
(b) Use interval notation to denote the set of all real num-
bers x that satisfy x 2.
2. The cost c of manufacturing x items is given by c .7x
19.6 and the revenue r from selling these items is given by
r 1.1x. How many items must be sold for the company to
break even (that is, for revenue to equal cost)?
Chapter
1
Test

3. The atmospheric pressure a (in pounds per square foot) at
height h thousand feet above sea level is approximately
a .8315h
2
73.93h 2116.1 (0 h 40).
(a) Find the atmospheric pressure (rounded to two decimal
places) at the top of Mount Annapurna (26,504 feet).
(b) The atmospheric pressure at the top of Mount Rainier
is 1238.41 pounds per square foot. How high (to the
nearest foot) is Mount Rainier?
4. The gross federal debt was about $5622 billion in 2000, when
the U.S. population was approximately 281.1 million people.
(a) Express the debt in scientific notation.
(b) Express the population in scientific notation.
(c) In 2000, what was each person’s share of the federal
debt?
5. Solve for t:
3
1
t
4
3
t
1
1
2t
1.
6. Solve for x:2x
2
13x 7 0.
7. Express the infinite decimal .14141414
…
as a fraction,
without using a calculator. Show your work.
8. Solve for b: E
h
2
(b c).
9. Solve for x:4x
2
6x 5.
10. (a) Describe in words the solutions of x 16 6.
(b) Use absolute value to describe all real numbers c that
are more than 5 units from 16 on the number line.
11. Find a real number k such that the equation
x
2
kx 16 0 has exactly one real solution.
12. Express each of the following without using absolute value
bars. Assume x 1.
(a) y
2
2y 1
(b) x
2
1
13. Solve for x: 4x 5 12.
Sections 1.3 and 1.4; Special Topics 1.2.B
14. Find the equation of the circle that passes through
(7, 5) and has center (1, 6).
15. Two lines have equations
4x y 4 0 and 6x 3y 13 0.
Are the lines parallel, perpendicular, or neither? Given rea-
sons for your answer.
16. (a) Find the midpoint of the line segment joining (1, 3)
and (2, 1).
(b) Find the length of the line segment in part (a).
17. Find the slope of the line through (5
, 6) and (5, 8).
18. Find the x-intercepts and y-intercepts of the graph of 3x
2
x y 2 0. You need not graph the equation.
19. The poverty level income for a family of four was $13,359
in 1990. It grew approximately linearly to $19,309 in 2004.
(a) At what rate was the poverty level increasing during
this period?
(b) Estimate the poverty level in 2000.
(c) Assuming the growth rate remains the same, estimate
the poverty level in 2010.
20. If P is a point on a circle with center C, then the tangent line
to the circle at P is the straight line through P that is per-
pendicular to the radius CP.
(a) Find the center C of the circle
(x 1)
2
(y 1)
2
5.
(b) Find the equation of the tangent line to this circle at the
point P (2, 3).
21. Find the center and the radius of the circle whose
equation is
3x
2
3y
2
6x 24 24y.
22. Graph the equation 2x 5y 10. Label all intercepts.
23. Find the perimeter of the shaded area in the figure.
24. The age-adjusted death rate from heart disease was 412.1
per 100,000 population in 1980 and 232.3 in 2003.
(a) Assuming that the death rate declined linearly, find an
equation of the form y mx b that gives the number
y of deaths per 100,000 in year x, with x 0 correspon-
ding to 1980. Round m to two decimal places.
(b) Use the equation in part (a) to estimate the death rate in
2001.
(c) Assuming that the equation remains accurate, estimate
the death rate in 2009.
(d) Is the equation likely to remain accurate over the next
three decades? Give reasons for your answer.
25. If r varies inversely as t and r 9 when t 3, find r when
t 12.
26. Determine whether the line through P and Q is parallel,
or perpendicular to the line through R and S, or neither,
when
P
0,
3
2
, Q (1, 1), R (6, 4), and S (7, 5).
1
12345
(2, 2)
2
3
4
5
y
x
74 CHAPTER 1 Basics

75
DISCOVERY PROJECT 1 Taxicab Geometry
A man was arrested in New York City in 2002 for selling drugs within 1000 feet of
a school. This carries a heavier penalty than does a sale more than 1000 feet from the
school. In a case that went to the state’s highest court, the man argued that his dis-
tance from the school should not be measured “as the crow flies” but as a person
would have to walk along the street (being unable to cut through buildings that the
crow would fly over). In his case, the walking distance was more than 1000 feet. The
court rejected his argument and he is now servinga6to12year sentence.*
Measuring distance as one walks—or as a taxi drives—from one point in the
city to another is an example of taxicab geometry. The taxicab distance from
point A to point B in Figure 1 is defined to be the sum u v, whereas the ordinary
(crow flying) distance is the length of the red line (
u
2
v
2
according to the
Pythagorean Theorem).
Figure 1
Find the taxicab distance and the ordinary distance between each pair of points.
1. (1, 1) and (5, 4)
2. (0, 0) and (500, 500)
3. (0, 0) and (1000, 0)
W. 42nd St.
W. 42nd St.
W
. 43rd St.
W. 43rd St.
W. 44th
St.
W. 44th
St.
W. 45th St.
W. 4 5
th St.
W. 41st St.
W. 41st St.
W. 40th St.
W. 40th St.
W. 39th St.
W. 39th St.
9th Ave.
9th Ave.
8th Ave.
8th Ave.
7th Ave.
7
t
hAve.
42nd St.
Time
4
2nd St. Time
Square N.R.S.
Square N.R.S.
W. 42nd St.
W. 43rd St.
W. 44th St.
W. 45th St.
W. 41st St.
W. 40th St.
W. 39th St.
W. 38th St.
W. 38th St.
W. 38th St.
9th Ave.
8th Ave.
7th Ave.
42nd St. T
ime
Square N.R.S.
u
2
v
2
u
v
B
A
*The same issue (with a different outcome) arose in a federal court. In a case involving the Family and
Medical Leave Act, the 10th Circuit Court of Appeals upheld a Labor Department rule requiring that
distance be measured in “surface miles, using surface transportation” rather than the distance as the
crow flies. See The New York Times of November 23, 2005 and May 28, 2007.
© B.A.E. Inc./Alamy
