Hungerford T.W., Shaw D.J. Contemporary Precalculus: A Graphing Approach
Подождите немного. Документ загружается.

(a) Which graph is the interest portion and which is the principal portion?
(b) At the end of ten years (120 months), about how much of each payment goes
for interest and how much for the principal?
SOLUTION
(a) The interest portion of the payment is the monthly interest due on the unpaid
balance. This balance (and hence, the interest) is large at the beginning but
slowly decreases as more payments are made. So the interest graph begins
high and ends low—it must be graph A. Consequently, graph B shows the
portion of each payment that goes to reducing the principal.
(b) The point (120, 600) on graph A shows that about $600 of the $850 payment
was for interest. Hence, $250 was for principal, as the point (120, 250) on
graph B indicates. ■
CIRCLES
If (c, d) is a point in the plane and r a positive number, then the circle with cen-
ter (c, d) and radius r consists of all points (x, y) that lie r units from (c, d ), as
shown in Figure 1–23. According to the distance formula, the statement that “the
distance from (x, y) to (c, d) is r units” is equivalent to:
(x c
)
2
(
y d)
2
r
Squaring both sides shows that (x, y) satisfies this equation:
(x c)
2
(y d)
2
r
2
Reversing the procedure shows that any solution (x, y) of this equation is a point
on the circle. Therefore
We say that (x c)
2
(y d)
2
r
2
is the equation of the circle with center
(c, d) and radius r.
46 CHAPTER 1 Basics
(c, d)
(x, y)
r
Figure 1–23
Circle
Equation
The circle with center (c, d) and radius r is the graph of
(x c)
2
(y d)
2
r
2
.
EXAMPLE 10
Identify the graph of the equation (x 4)
2
(y 2)
2
9.
SOLUTION Since 9 3
2
, we can write the equation as
(x 4)
2
(y 2)
2
3
2
.
Now the equation is of the form shown in the box above, with c 4, d 2
and r 3. So the graph is a circle with center (4, 2) and radius 3, as shown in
Figure 1–24. ■
120
A
B
60 180 300240
Months
360
x
y
200
100
400
300
600
500
800
700
900
Figure 1–22
2
−1
42
4
x
y
6
Figure 1–24

EXAMPLE 11
Find the equation of the circle with center (3, 2) and radius 2 and sketch its
graph.
SOLUTION Here the center is (c, d) (3, 2) and the radius is r 2, so the
equation of the circle is
(x c)
2
( y d)
2
r
2
[x (3)]
2
( y 2)
2
2
2
(x 3)
2
( y 2)
2
4.
Its graph is shown in Figure 1–25. ■
EXAMPLE 12
Find the equation of the circle with center (3, 1) that passes through (2, 4).
SOLUTION We must first find the radius. Since (2, 4) is on the circle, the
radius is the distance from (2, 4) to (3, 1) as shown in Figure 1–26, namely,
(2 3
)
2
(4
(
1))
2
1 25
26.
The equation of the circle with center at (3, 1) and radius 26 is
(x 3)
2
(y (1))
2
(26)
2
(x 3)
2
(y 1)
2
26
x
2
6x 9 y
2
2y 1 26
x
2
y
2
6x 2y 16 0. ■
The equation of any circle can always be written in the form
x
2
y
2
Bx Cy D 0
for some constants B, C, D, as in Example 12 (where B 6, C 2, D 16).
Conversely, the graph of such an equation can always be determined.
EXAMPLE 13
Show that the graph of
3x
2
3y
2
12x 30y 45 0
is a circle and find its center and radius.
SOLUTION We will be completing the square, which requires that x
2
and y
2
each have coefficient 1. So we begin by dividing both sides of the equation by 3
and regrouping the terms.
x
2
y
2
4x 10y 15 0
(x
2
4x) (y
2
10y) 15.
SECTION 1.3 The Coordinate Plane 47
2
2
1
−11−2−3−4−5
3
4
x
y
(−3, 2)
Figure 1–25
(3, −1)
(2, 4)
x
y
26
Figure 1–26

Next we complete the square in both expressions in parentheses (see page 22). To
complete the square in x
2
4x, we add 4 (the square of half the coefficient of x),
and to complete the square in y
2
10y, we add 25 (why?). To have an equivalent
equation, we must add these numbers to both sides:
(x
2
4x 4) (y
2
10y 25) 15 4 25
(x 2)
2
(y 5)
2
14
Since 14 (14)
2
, this is the equation of the circle with center (2, 5) and
radius 14. ■
When the center of a circle of radius r is at the origin (0, 0), its equation takes
a simpler form.
48 CHAPTER 1 Basics
Circle at
the Origin
The circle with center (0, 0) and radius r is the graph of
x
2
y
2
r
2
.
Proof Substitute c 0 and d 0 in the equation for the circle with center (c, d)
and radius r.
(x c)
2
(y d)
2
r
2
(x 0)
2
(y 0)
2
r
2
x
2
y
2
r
2
. ■
EXAMPLE 14
Letting r 1 shows that the graph of x
2
y
2
1 is the circle of radius 1 centered
at the origin, as shown in Figure 1–27. This circle is called the unit circle. ■
y
2
1
−1
−2
−1−221
x
Figure 1–27
1. Find the coordinates of points A–I.
I
C
D
E
BA
G
H
1
2
3
321
F
In Exercises 2–5, find the coordinates of the point P.
2. P lies 4 units to the left of the y-axis and 5 units below the
x-axis.
3. P lies 3 units above the x-axis and on the same vertical line
as (6, 7).
4. P lies 2 units below the x-axis, and its x-coordinate is three
times its y-coordinate.
5. P lies 4 units to the right of the y-axis, and its y-coordinate
is half its x-coordinate.
EXERCISES 1.3
SECTION 1.3 The Coordinate Plane 49
Year 2000 2001 2002 2003 2004 2005
Tuition
and Fees 3487 3725 4081 4694 5127 5491
Year Number Sold
2000 257,000
2001 129,000
2002 143,000
2003 214,000
2004 315,000
2005 485,000
*eBrain Market Research
7.
The table shows sales of personal digital video recorders.*
Let x 0 correspond to 2000, and measure y in thousands.
8. The maximum yearly contribution to an individual retire-
ment account (IRA) was $3000 in 2003. It changed to
$4000 in 2005 and will change to $5000 in 2008. Assuming
3% inflation, however, the picture is somewhat different.
The table shows the maximum IRA contribution in fixed
2003 dollars. Let x 0 correspond to 2000.
In Exercises 6–8, sketch a scatter plot and a line graph of the
given data.
6. Tuition and fees at four-year public colleges in the fall of
each year are shown in the table (Source: The College
Board). Let x 0 correspond to 2000.
9. (a) If the first coordinate of a point is greater than 3 and its
second coordinate is negative, in what quadrant does
it lie?
(b) What is the answer in part (a) if the first coordinate is
less than 3?
10. In what quadrant(s) does a point lie if the product of its
coordinates is
(a) positive? (b) negative?
11. (a) Plot the points (3, 2), (4, 1), (2, 3), and (5, 4).
(b) Change the sign of the y-coordinate in each of the
points in part (a), and plot these new points.
Year Maximum Contribution
2003 3000
2004 2910
2005 3764
2006 3651
2007 3541
2008 4294
(c) Explain how the points (a, b) and (a, b) are related
graphically. [Hint: What are their relative positions
with respect to the x-axis?]
12. (a) Plot the points (5, 3), (4, 2), (1, 4), and (3, 5).
(b) Change the sign of the x-coordinate in each of the
points in part (a), and plot these new points.
(c) Explain how the points (a, b) and (a, b) are related
graphically. [Hint: What are their relative positions
with respect to the y-axis?]
In Exercises 13–20, find the distance between the two points
and the midpoint of the segment joining them.
13. (3, 5), (2, 7) 14. (2, 4), (3, 6)
15. (2, 5), (1, 2) 16. (2, 3), (3, 2)
17. (2
, 1), (3
, 2) 18. (1, 5
), (2
, 3
)
19. (a, b), (b, a) 20. (s, t), (0, 0)
21. Which of the following points is closest to the origin?
(4, 4.2), (3.5, 4.6), (3, 5), (2, 5.5)
22. Which of the following points is closest to (3, 2)?
(0, 0), (4, 5.3), (.6, 1.5), (1, 1)
23. Find the perimeter of the shaded region in the figure.
24. What is the perimeter of the triangle with vertices (1, 1),
(5, 4), and (2, 5)?
25. Find the area of the shaded region in Exercise 23. [Hint:
What is the area of the triangle with vertices (4, 0), (2, 2),
and (4, 5)?]
26. Find the area of the triangle with vertices (1, 4), (4, 3), and
(2, 5). You may assume that there is a right angle at
vertex (1, 4).
In Exercises 27–29, show that the three points are the vertices
of a right triangle, and state the length of the hypotenuse. [You
may assume that a triangle with sides of lengths a, b, c is a
right triangle with hypotenuse c provided that a
2
b
2
c
2
.]
27. (0, 0), (1, 1), (2, 2)
28. (3, 2), (0, 4), (2, 3)
29. (1, 4), (5, 2), (3, 2)
4
2
204
(2, 2)
0
y
x
30. Suppose a baseball playing field is placed on the coordinate
plane, as in Example 3.
(a) Find the coordinates of first and third base.
(b) If the left fielder is at the point (50, 325), how far is he
from first base?
(c) How far is the left fielder in part (b) from the right
fielder, who is at the point (280, 20)?
31. A standard football field is 100 yards long and 53
1
3
yards
wide. The quarterback, who is standing on the 10-yard line,
20 yards from the left sideline, throws the ball to a receiver
who is on the 45-yard line, 5 yards from the right sideline,
as shown in the figure.
(a) How long was the pass? [Hint: Place the field in the first
quadrant of the coordinate plane, with the left sideline
on the y-axis and the goal line on the x-axis. What are the
coordinates of the quarterback and the receiver?]
(b) A player is standing halfway between the quarterback
and the receiver. What are his coordinates?
32. How far is the quarterback in Exercise 31 from a player who
is on the 50-yard line, halfway between the sidelines?
33. The number of passengers annually on U.S. commercial
airlines was 650 million in 2002 and is expected to be 1.05
billion in 2016.*
(a) Represent this data graphically by two points.
(b) Find the midpoint of the line segment joining these two
points.
(c) How might this midpoint be interpreted? What assump-
tions, if any, are needed to make this interpretation?
34. The net revenues of Pepsico were $26,971 million in 2003 and
$32,562 million in 2005.
†
Estimate the net revenue in 2004.
In Exercises 35–40, determine whether the point is on the
graph of the given equation.
35. (2, 1); 3x y 5 0
36. (2, 1); x
2
y
2
6x 8y 15
50
40
Goal line
Quarterback
Receiver
30
20
10
50 CHAPTER 1 Basics
*Federal Aviation Agency.
†
Pepsico annual reports.
37.
(6, 2); 3y x 12
38. (1, 2); 3x y 12
39. (1, 4); (x 2)
2
(y 5)
2
4
40. (1, 1);
x
2
2
y
3
2
1
In Exercises 41–46, find the x- and y-intercepts of the graph of
the equation.
41. x
2
6x y 5 0
42. x
2
2xy 3y
2
1
43. (x 2)
2
y
2
9
44. (x 1)
2
(y 2)
2
4
45. 9x
2
24xy 16y
2
90x 128y 0
46. 2x
2
4xy 2y
2
3x 5y 10
47. The graph on the next page, which is based on data from the
Actuarial Society of South Africa and assumes no changes
in current behavior, shows the projected new cases of AIDS
in South Africa (in millions) in coming years (x 0 corre-
sponds to 2000).
(a) Estimate the number of new cases in 2010.
(b) Estimate the year in which the largest number of new
cases will occur. About how many new cases will there
be in that year?
(c) In what years will the number of new cases be below
7,000,000?
−1
1
y
−2 −1
0
21
x
3
1
−2−42468
−3
−1
−5
−7
5
x
y
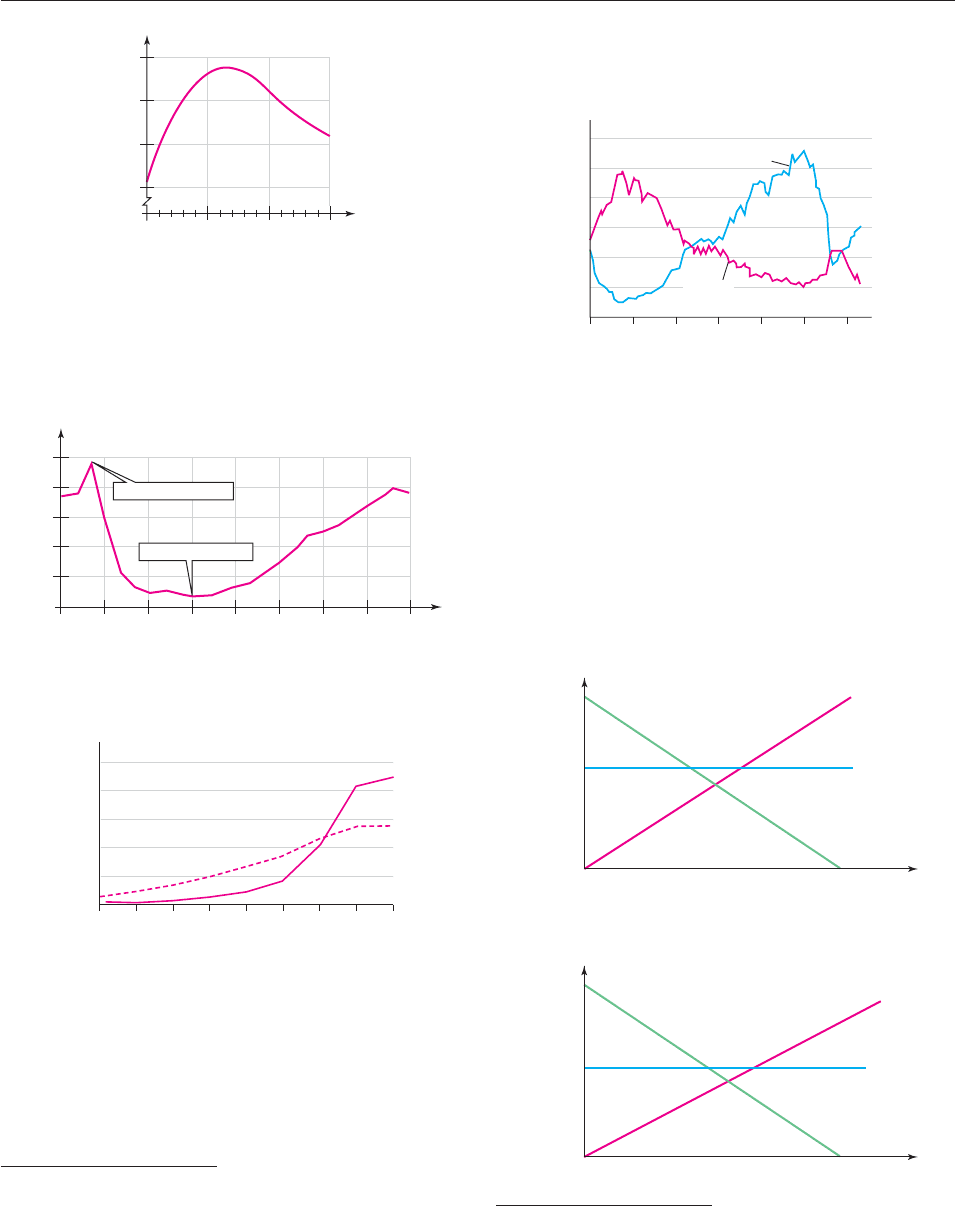
48. The graph shows the total number of alcohol-related car
crashes in Ohio at a particular time of the day for the years
1991–2000.* Time is measured in hours after midnight.
During what periods is the number of crashes
(a) below 5000?
(b) above 15,000?
49. Many companies are changing their traditional employee
pension plans to so-called cash balance plans. The graph
shows pension accrual by age for two hypothetical plans.
†
(a) Assuming that you can take your accrued pension
benefits in cash when you leave the company before
retirement, for what age group is the cash balance plan
better?
(b) At what age is the accrued amount the same for either
type of pension plan?
(c) If you remain with the company until retirement, how
much better off are you with a traditional instead of a
cash balance plan?
$100,000
80,000
60,000
40,000
20,000
0
25 30 35 40 45 50 55 60 65
Traditional
pension
Cash balance
pension
20,000
25,000
15,000
5000
10,000
0
2421181512963
0
y
x
2 A.M.: 24,486 crashes
9
A.M.: 2,051 crashes
7
8
6
5
501015
0
y
x
SECTION 1.3 The Coordinate Plane 51
50. In an ongoing consumer confidence survey, respondents are
asked two questions: Are jobs plentiful? Are jobs hard to
get? The graph shows the percentage of people answering
“yes” to each question over the years.*
(a) In what year did the most people feel that jobs were
plentiful? In that year, approximately what percentage
of people felt that jobs were hard to get?
(b) In what year did the most people feel that jobs were
hard to get? In that year approximately what percentage
of people felt that jobs were plentiful?
(c) In what years was the percentage of those who thought
jobs were plentiful the same as the percentage of those
that thought jobs were hard to get?
In Exercises 51–54, determine which of graphs A, B, C best
describes the given situation.
51. You have a job that pays a fixed salary for the week. The
graph shows your salary.
52. You have a job that pays an hourly wage. The graph shows
your salary.
Income
Hours worked
A
B
C
Income
Hours worked
A
B
C
Jobs are
hard to get
Jobs are
plentiful
0
10
20
30
40
50
60%
’90
’92 ’94 ’96 ’98 ’00 ’02
*The Cleveland Plain Dealer.
†
Data from Steve J. Kopp and Lawrence W. Sher, The Pension Forum,
Vol 11, No. 1. Graph from “What if a Pension Shift Hit Lawmakers
Too?” by M. W. Walsh, New York Times, March 9, 2003. Copyright
© 2003 The New York Times Co.
*Data for The Conference Board. Graph from “Tight U.S. Job Market
Adds to Jitters Among Consumers.” by A. Berenson, The New York
Times, March 1, 2003. Copyright © 2003 The New York Times Co.
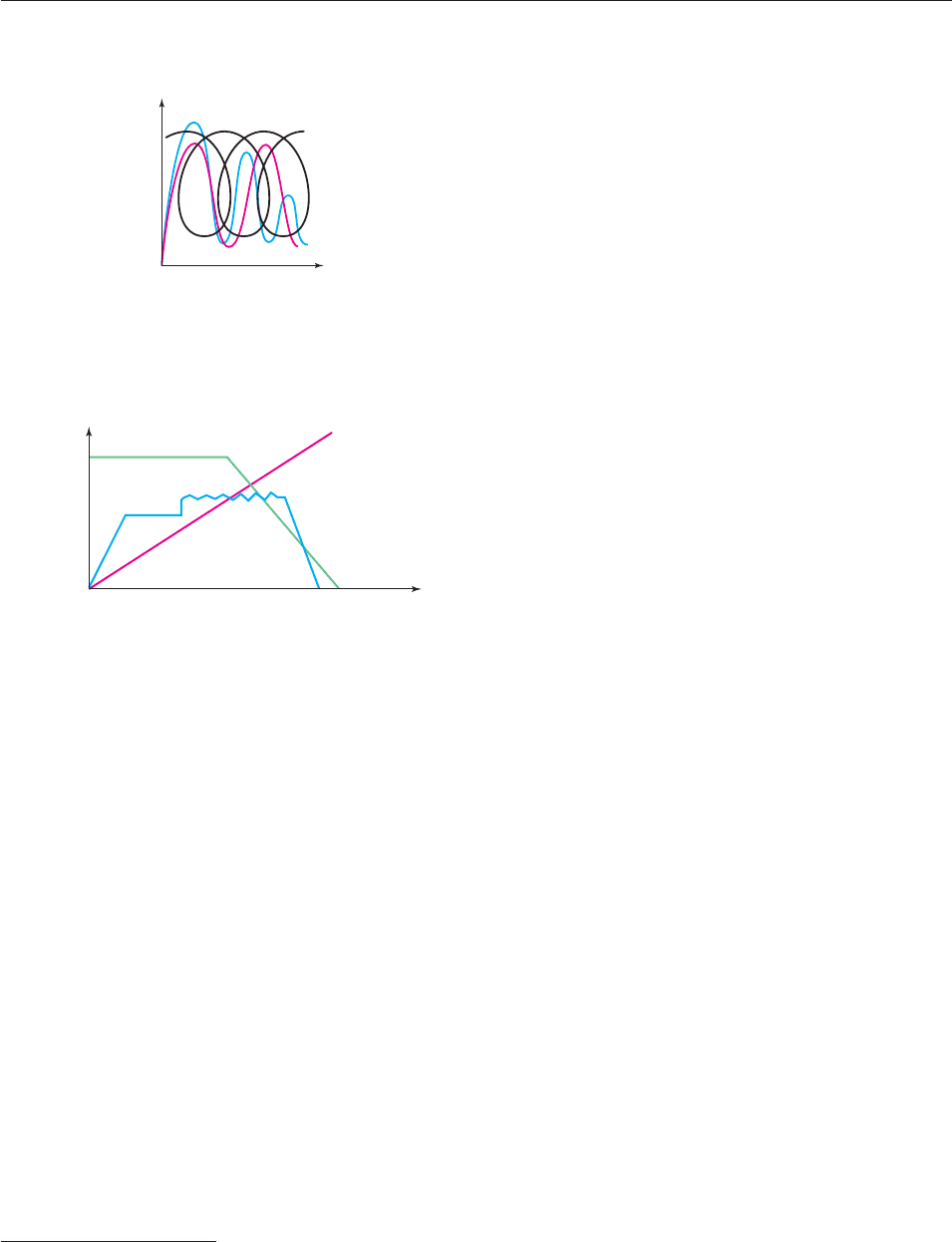
53. You take a ride on a Ferris wheel. The graph shows your
distance from the ground.*
54. Alison’s wading pool is filled with a hose by her big sister
Emily, and Alison plays in the pool. When they are finished,
Emily empties the pool. The graph shows the water level of
the pool.
In Exercises 55–58, find the equation of the circle with given
center and radius r.
55. (3, 4); r 2 56. (3, 5); r 3
57. (0, 0); r 3
58. (5, 2); r 1
In Exercises 59–62, sketch the graph of the equation. Label the
x- and y-intercepts.
59. (x 5)
2
(y 2)
2
5
60. (x 6)
2
y
2
4
61. (x 1)
2
(y 3)
2
9
62. (x 2)
2
(y 4)
2
1
In Exercises 63–68, find the center and radius of the circle
whose equation is given.
63. x
2
y
2
8x 6y 15 0
64. 15x
2
15y
2
10
65. x
2
y
2
6x 4y 15 0
66. x
2
y
2
10x 75 0
67. x
2
y
2
25x 10y 12
68. 3x
2
3y
2
12x 12 18y
Water level
Time
A
B
C
Time elapsed
B
A
C
Distance from ground
52 CHAPTER 1 Basics
69. Determine whether each point lies inside, or outside, or on
the circle
(x 1)
2
(y 3)
2
4.
(a) (2.2, 4.6) (b) (.2, 4.7) (c) (.1, 1.4)
(d) (2.6, 4.3) (e) (.6, 1.8)
70. Do the circles with the following equations intersect?
(x 3)
2
(y 2)
2
25 and (x 3)
2
(y 2)
2
4
[Hint: Consider the radii and the distance between the
centers.]
In Exercises 71–78, find the equation of the circle.
71. Center (3, 3); passes through the origin.
72. Center (1, 3); passes through (4, 2).
73. Center (1, 2); intersects x-axis at 1 and 3.
74. Center (3, 1); diameter 2.
75. Center (5, 4); tangent (touching at one point) to the
x-axis.
76. Center (2, 6); tangent to the y-axis.
77. Endpoints of a diameter are (3, 3) and (1, 1).
78. Endpoints of a diameter are (3, 5) and (7, 5).
79. One diagonal of a square has endpoints (3, 1) and
(2, 4). Find the endpoints of the other diagonal.
80. Find the vertices of all possible squares with this property:
Two of the vertices are (2, 1) and (2, 5). [Hint: There are
three such squares.]
81. Do Exercise 80 with (c, d ) and (c, k) in place of (2, 1) and
(2, 5).
82. Find the three points that divide the line segment from
(4, 7) to (10, 9) into four parts of equal length.
83. Find all points P on the x-axis that are 5 units from (3, 4).
[Hint: P must have coordinates (x, 0) for some x and the
distance from P to (3, 4) is 5.]
84. Find all points on the y-axis that are 8 units from (2, 4).
85. Find all points with first coordinate 3 that are 6 units from
(2, 5).
86. Find all points with second coordinate 1 that are 4 units
from (2, 3).
87. Find a number x such that (0, 0), (3, 2), and (x, 0) are the
vertices of an isosceles triangle, neither of whose two equal
sides lie on the x-axis.
88. Do Exercise 87 if one of the two equal sides lies on the
positive x-axis.
89. Show that the midpoint M of the hypotenuse of a right
triangle is equidistant from the vertices of the triangle.
[Hint: Place the triangle in the first quadrant of the plane,
with right angle at the origin so that the situation looks like
the figure.]
*Mathematics Teacher, Vol. 95, No. 9, December 2002.

90. Show that the diagonals of a parallelogram bisect each
other. [Hint: Place the parallelogram in the first quadrant
with a vertex at the origin and one side along the x-axis so
that the situation looks like the figure.]
91. Show that the diagonals of a rectangle have the same length.
[Hint: Place the rectangle in the first quadrant of the plane
and label its vertices appropriately, as in Exercises 89–90.]
92. If the diagonals of a parallelogram have the same length,
show that the parallelogram is actually a rectangle. [Hint:
See Exercise 90.]
THINKERS
93. For each nonzero real number k, the graph of
(x k)
2
y
2
k
2
is a circle. Describe all possible such
circles.
(c, 0)
(a, b)
(a + c, b)
y
x
c
c
(s, 0)
(0, r)
y
x
M
SECTION 1.4 Lines 53
94. Suppose every point in the coordinate plane is moved
5 units straight up.
(a) To what point does each of these points go:(0, 5),
(2, 2), (5, 0), (5, 5), (4, 1)?
(b) Which points go to each of the points in part (a)?
(c) To what point does (a, b) go?
(d) To what point does (a, b 5) go?
(e) What point goes to (4a, b)?
(f ) What points go to themselves?
95. Let (c, d) be any point in the plane with c 0. Prove that
(c, d) and (c, d) lie on the same straight line through the
origin, on opposite sides of the origin, the same distance
from the origin. [Hint: Find the midpoint of the line seg-
ment joining (c, d) and (c, d).]
96. Proof of the Midpoint Formula Let P and Q be the points
(x
1
, y
1
) and (x
2
, y
2
), respectively, and let M be the point with
coordinates
x
1
2
x
2
,
y
1
2
y
2
.
Use the distance formula to compute the following:
(a) The distance d from P to Q;
(b) The distance d
1
from M to P;
(c) The distance d
2
from M to Q.
(d) Verify that d
1
d
2
.
(e) Show that d
1
d
2
d. [Hint: Verify that d
1
1
2
d and
d
2
1
2
d.]
(f ) Explain why parts (d) and (e) show that M is the mid-
point of PQ.
1.4 Lines
■ Find the slope of a line.
■ Understand what its slope tells you about a line.
■ Construct and interpret the slope-intercept form of the equation
of a line.
■ Identify the equations of horizontal and vertical lines.
■ Use point-slope form of the equation of a line.
■ Recognize the general form of the equation of a line.
■ Understand the relationship between parallel lines and their
equations.
■ Understand the relationship between perpendicular lines and
their equations.
■ Interpret slope as a rate of change.
Section Objectives
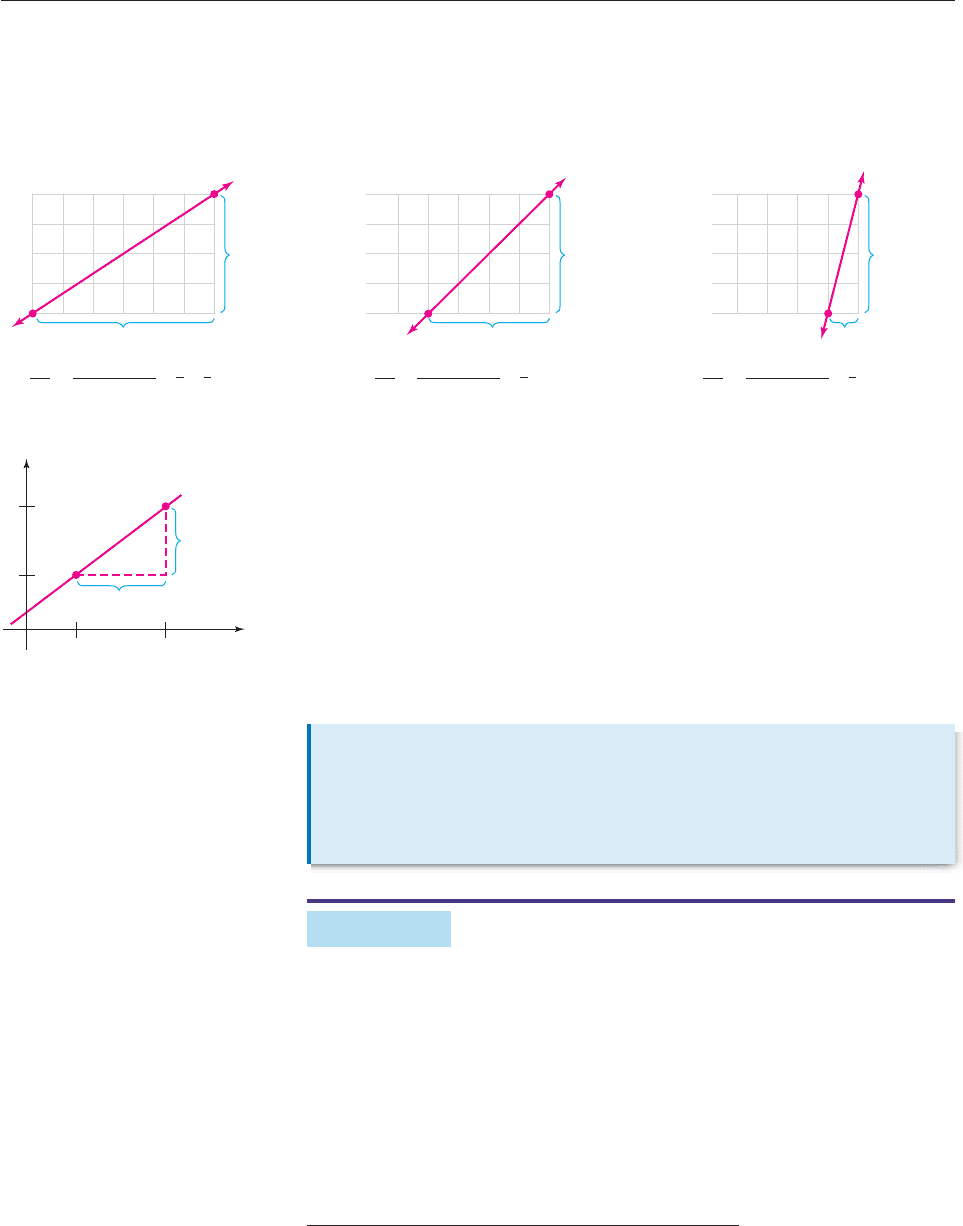
When you move from a point P to a point Q on a line,* two numbers are involved,
as illustrated in Figure 1–28:
(i) The vertical distance you move (the change in y, denoted y);
(ii) The horizontal distance you move (the change in x, denoted x).
†
Figure 1–28
The number
c
c
h
h
a
a
n
n
g
g
e
e
i
i
n
n
y
x
measures the steepness of the line: the steeper the line,
the larger the number. In Figure 1–28, the grid allowed us to measure the change
in y and the change in x. When the coordinates of P and Q are given, as in Fig-
ure 1–29, then:
The change in y is the difference of the y-coordinates of P and Q;
The change in x is the difference of the x-coordinates of P and Q.
Consequently, we have the following definition.
Change in x = 6
Change in x
Change in y
4
6
(a)
==
Change
in y = 4
P
Q
2
3
∆x
∆y
=
∆x
∆y
=
∆x
∆y
=
Change in x = 1
Change in x
Change in y
4
1
(c)
=
Change
in y = 4
P
Q
Change in x = 4
Change in x
Change in y
4
4
(b)
== 1 = 4
Change
in y = 4
P
Q
54 CHAPTER 1 Basics
*In this section, “line” means “straight line” and movement is from left to right.
†
(pronounced “delta”) is the Greek letter D.
EXAMPLE 1
Find the slope of the line through the two points.
(a) (0, 1) and (4, 1) (b) (2, 3) and (2, 1)
(c) (1, 1) and (3, 1) (d) (3, 1) and (3, 2)
SOLUTION
(a) We apply the formula in the preceding box, with x
1
0, y
1
1 and x
2
4,
y
2
1:
Slope
y
x
y
x
2
2
y
x
1
1
1
4
(
0
1)
2
4
1
2
.
Slope of
a Line
If (x
1
, y
1
) and (x
2
, y
2
) are points with x
1
x
2
, then the slope of the line
through these points is the number
y
x
c
c
h
h
a
a
n
n
g
g
e
e
i
i
n
n
y
x
y
x
2
2
y
x
1
1
.
y
(x
1
, y
1
)
(x
2
, y
2
)
P
Q
y
2
− y
1
x
2
− x
1
y
2
y
1
x
1
x
2
x
Figure 1–29

The order of the points makes no difference; if you use (4, 1) for (x
1
, y
1
) and
(0, 1) for (x
2
, y
2
), you obtain the same number:
Slope
y
x
y
x
2
2
y
x
1
1
0
1
4
1
2
4
1
2
.
The slope is positive and the line through the two points rises from left to
right, as shown in Figure 1–30.
(b) We have (x
1
, y
1
) (2, 3) and (x
2
, y
2
) (2, 1), as shown in Figure 1–31.
Hence,
Slope
y
x
y
x
2
2
y
x
1
1
2
1
(
3
2)
4
4
1.
The slope is negative and the line through the points falls from left to
right.
(c) The points (1, 1) and (3, 1) lie on a horizontal line, as shown in Figure 1–32,
and
Slope
y
x
y
x
2
2
y
x
1
1
1
3
1
1
0
2
0.
A similar argument shows that every horizontal line has slope 0.
(d) Figure 1–33 shows that the points lie on a vertical line. Applying the slope
formula to (x
1
, y
1
) (3, 1) and (x
2
, y
2
) (3, 2) yields
Slope
y
x
2
2
y
x
1
1
2
3
(
3
1)
3
0
not defined!
The same argument works for any vertical line: the slope of a vertical line is
not defined. ■
SECTION 1.4 Lines 55
y
1
−1
1
234
x
Figure 1–30
−1
1
2
3
−2
x
y
−2 −1
21
Figure 1–31
−1
1
2
3
−2
x
y
−1
231
Figure 1–32
−1
1
2
3
−2
x
y
−1
2341
Figure 1–33
EXAMPLE 2
The lines shown in Figure 1–34 on the next page are determined by these points:
L
1
: (1, 1) and (0, 2) L
2
: (0, 2) and (2, 4) L
3
: (6, 2) and (3, 2)
L
4
: (3, 5) and (3, 1) L
5
: (1, 0) and (2, 2).
Their slopes are as follows:
CAUTION
When finding slopes, you must subtract the y-coordinates and x-coordinates in the same order.
With the points (3, 4) and (1, 8), for instance, if you use 8 4 in the numerator, you must use
1 3 in the denominator (not 3 1).
