Hungerford T.W., Shaw D.J. Contemporary Precalculus: A Graphing Approach
Подождите немного. Документ загружается.

105. c d if c d 106. c d if c d
107. u v v u 108.
u
v
u
v
if u v, u 0, v 0
In Exercises 109 and 110, explain why the given statement is
true for any numbers c and d. [Hint: Look at the properties of
absolute value on page 10.]
109. (c d)
2
c
2
2cd d
2
110.
9c
2
18cd
9d
2
3c d
In Exercises 111–116, express the given geometric statement
about numbers on the number line algebraically, using
absolute values.
111. The distance from x to 5 is less than 4.
112. x is more than 6 units from c.
113. x is at most 17 units from 4.
114. x is within 3 units of 7.
115. c is closer to 0 than b is.
116. x is closer to 1 than to 4.
In Exercises 117–120, translate the given algebraic state-
ment into a geometric statement about numbers on the num-
ber line.
117. x 3 2 118. x c 6
119. x 7 3 120. u v 2
121. Match each of the following graphs with the appropriate
absolute value equation or inequality.
(a) i. x 17 7
(b) ii. x 17 7
(c) iii. x 17 7
(d) iv. x 17 7
(e) v. x 17 7
122. Explain geometrically why this statement is always false:
c 1 2 and simultaneously c 12 3.
In Exercises 123–134, use the geometric approach explained in
the text to solve the given equation or inequality.
123. x 1 124. x 3/2
125. x 2 1 126. x 3 2
127. x p 4 128.
x
3
2
5
129. x 7 130. x 5
131. x 5 2 132. x 6 2
133. x 2 3 134. x 4 2
THINKERS
135. Explain why the statement a b c 0 is algebraic
shorthand for “at least one of the numbers a, b, c, is dif-
ferent from zero.”
136. Find an algebraic shorthand version of the statement “none
of the numbers a, b, c, is zero.”
2410
2410
2410
16 CHAPTER 1 Basics
1.1.A SPECIAL TOPICS Decimal Representation of Real Numbers
■ Convert a repeating decimal to a rational number, and vice versa.
■ Distinguish between rational and irrational numbers.
Every rational number can be expressed as a terminating or repeating decimal.
For instance, 3/4 .75. To express 15/11 as a decimal, divide the numerator by
the denominator:
1.3636
15.0000
11
40
33
70
66
40
33
70
66
11
Same remainder
Repeats as above
Section Objectives
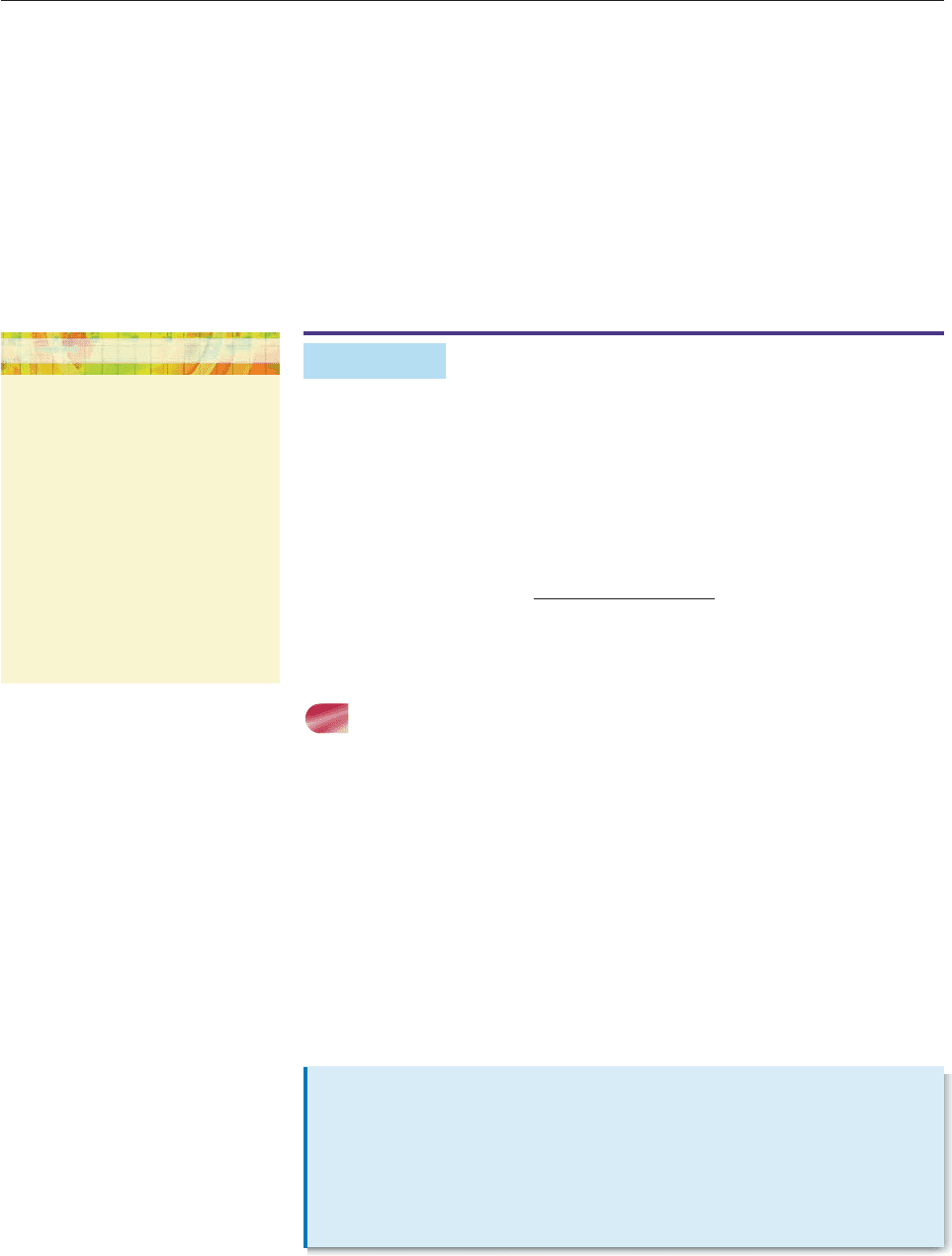
Since the remainder at the first step (namely, 4) occurs again at the third step, it
is clear that the division process goes on forever with the two-digit block “36”
repeating over and over in the quotient 15/11 1.3636363636 .
The method used in the preceding example can be used to express any
rational number as a decimal. During the division process, some remainder nec-
essarily repeats. If the remainder at which this repetition starts is 0, the result is a
repeating decimal ending in zeros—that is, a terminating decimal (for instance,
.75000 .75). If the remainder at which the repetition starts is nonzero, then
the result is a nonterminating repeating decimal, as in the example above.
Conversely, there is a simple method for converting any repeating decimal
into a rational number.
EXAMPLE 1
Write d .272727 as a rational number.
SOLUTION Assuming that the usual rules of arithmetic hold, we see that
100d 27.272727 and d .272727 .
Now subtract d from 100d:
100d 27.272727
d .272727
99d 27
Dividing both sides of this last equation by 99 shows that d 27/99 3/11. ■
IRRATIONAL NUMBERS
Many nonterminating decimals are nonrepeating (that is, no block of digits
repeats forever), such as .202002000200002 (where after each 2 there is one
more zero than before). Although the proof is too long to give here, it is true that
every nonterminating and nonrepeating decimal represents an irrational real
number. Conversely every irrational number can be expressed as a nonterminat-
ing and nonrepeating decimal (no proof to be given here).
A typical calculator can hold only the first 10–14 digits of a number in deci-
mal form. Consequently, a calculator can contain the exact value only of those
rational numbers whose decimal expansion terminates after 10–14 places. It must
approximate all other real numbers.
Since every real number is either a rational number or an irrational one, the
preceding discussion can be summarized as follows.
SPECIAL TOPICS 1.1.A Decimal Representation of Real Numbers 17
Decimal
Representation
1. Every real number can be expressed as a decimal.
2. Every decimal represents a real number.
3. The terminating decimals and the nonterminating repeating decimals
are the rational numbers.
4. The nonterminating, nonrepeating decimals are the irrational numbers.
TECHNOLOGY TIP
To convert repeating decimals to frac-
tions on TI, use Frac in this menu/
submenu:
TI-84: MATH
TI-86: MATH/MISC
On HP-39gs, select Fraction number
format in the MODE menu; then enter
the decimal.
On Casio, use the FRAC program in
the Program Appendix.

18 CHAPTER 1 Basics
In Exercises 1–6, express the given rational number as a
repeating decimal.
1. 79 2. 1988 3. 911
4. 213 5. 227 6. 119 (long)
In Exercises 7–13, express the given repeating decimal as a
fraction.
7. .373737 8. .929292
9. 76.63424242 [Hint: Consider 10,000d 100d, where
d 76.63424242 .]
10. 13.513513 [Hint: Consider 1000d d, where
d 13.513513 .]
11. .135135135 [Hint: See Exercise 10.]
12. .33030303 13. 52.31272727
14. If two real numbers have the same decimal expansion
through three decimal places, how far apart can they be on
the number line?
In Exercises 15–22, state whether a calculator can express the
given number exactly.
15. 2/3 16. 7/16 17. 1/64 18. 1/22
19. 3p/2 20. p 3 21. 1/.625 22. 1/.16
23. Use the methods in Exercises 7–13 to show that both
.74999 and .75000 are decimal expansions of 3/4.
[Every terminating decimal can also be expressed as a
decimal ending in repeated 9’s. It can be proved that these
are the only real numbers with more than one decimal
expansion.]
Finding remainders with a calculator
24. If you use long division to divide 369 by 7, you obtain:
52
Quotient
Divisor 7 369 Dividend
35
19
14
5
Remainder
If you use a calculator to find 369 7, the answer is dis-
played as 52.71428571. Observe that the integer part of this
calculator answer, 52, is the quotient when you do the prob-
lem by long division. The usual “checking procedure” for
long division shows that
7
52 5 369 or, equivalently 369 7
52 5.
Thus, the remainder is
Dividend (divisor)
integer part of
calculator answer
.
Use this method to find the quotient and remainder in these
problems:
(a) 5683 9 (b) 1,000,000 19
(c) 53,000,000 37
In Exercises 25–30, find the decimal expansion of the given
rational number. All these expansions are too long to fit in a
calculator but can be readily found by using the hint in
Exercise 25.
25. 1/17 [Hint: The first part of dividing 1 by 17 involves
working this division problem: 1,000,000 17. The
method of Exercise 24 shows that the quotient is 58,823 and
the remainder is 9. Thus the decimal expansion of 1/17 be-
gins .058823, and the next block of digits in the expansion
will be the quotient in the problem 9,000,000 17. The
remainder when 9,000,000 is divided by 17 is 13, so the
next block of digits in the expansion of 1/17 is the quotient
in the problem 13,000,000 17. Continue in this way until
the decimal expansion repeats.]
26. 3/19 27. 1/29 28. 3/43 29. 283/47
30. 768/59
THINKERS
31. If your calculator has a Frac key or program (see the Pro-
gram Appendix), test its limitations by entering each of the
following numbers and then pressing the Frac key.
(a) .058823529411 (b) .0588235294117
(c) .058823529411724 (d) .0588235294117985
Which of your answers are correct? [Hint: Exercise 25 may
be helpful.]
32. (a) Show that there are at least as many irrational numbers
(nonrepeating decimals) as there are terminating deci-
mals. [Hint: With each terminating decimal associate a
nonrepeating decimal.]
(b) Show that there are at least as many irrational numbers
as there are repeating decimals. [Hint: With each
repeating decimal, associate a nonrepeating decimal by
inserting longer and longer strings of zeros: for
instance, with .11111111 associate the number
.101001000100001 .]
EXERCISES 1.1.A
SECTION 1.2 Solving Equations Algebraically 19
*Any letter may be used for the variable.
Basic Principles for
Solving Equations
1.2 Solving Equations Algebraically
■ Understand the basic principles for solving equations.
■ Solve linear equations.
■ Solve quadratic equations by factoring, completing the square,
or using the quadratic formula.
■ Use the discriminant to determine the number of real solutions
of a quadratic equation.
■ Solve some types of higher-degree equations.
■ Solve fractional equations.
This section deals with equations such as
3x 6 7x 4, x
2
5x 6 0, 2x
4
13x
2
3.
A solution of an equation is a number that, when substituted for the variable
x, produces a true statement.* For example, 5 is a solution of 3x 2 17 because
3
5 2 17 is a true statement. To solve an equation means to find all its so-
lutions. Throughout this chapter, we shall deal only with real solutions, that is,
solutions that are real numbers.
Two equations are said to be equivalent if they have the same solutions. For
example, 3x 2 17 and x 2 3 are equivalent because 5 is the only solution
of each one.
The usual strategy in equation solving is to use these basic principles to transform
a given equation into an equivalent one whose solutions are known.
A first-degree, or linear, equation is one that can be written in the form
ax b 0
for some constants a, b, with a 0. Every first-degree equation has exactly one
solution, which is easily found.
EXAMPLE 1
To solve 3x 6 7x 4, we use the basic principles to transform this equation
into an equivalent one whose solution is obvious:
3x 6 7x 4
Add 6 to both sides: 3x 7x 10
Subtract 7x from both sides: 4x 10
Divide both sides by 4: x
10
4
5
2
.
Section Objectives
Performing any of the following operations on an equation produces an
equivalent equation:
1. Add or subtract the same quantity from both sides of the equation.
2. Multiply or divide both sides of the equation by the same nonzero quantity.
CAUTION
To guard against mistakes, check your
solutions by substituting each one in
the original equation to make sure it
really is a solution.
Since 5/2 is the only solution of this last equation, 5/2 is the only solution of
the original equation, 3x 6 7x 4. ■
EXAMPLE 2
Solve the equation a
2
x b
2
y 2 for y.
SOLUTION Since we are to solve for y, we treat y as the variable and treat all
other letters as constants. We begin by getting the y-term on one side and all other
terms on the other side of the equation.
a
2
x b
2
y 2
Subtract a
2
x from both sides: b
2
y 2 a
2
x
Divide both sides by b
2
: y
2
b
2
a
2
x
■
EXAMPLE 3
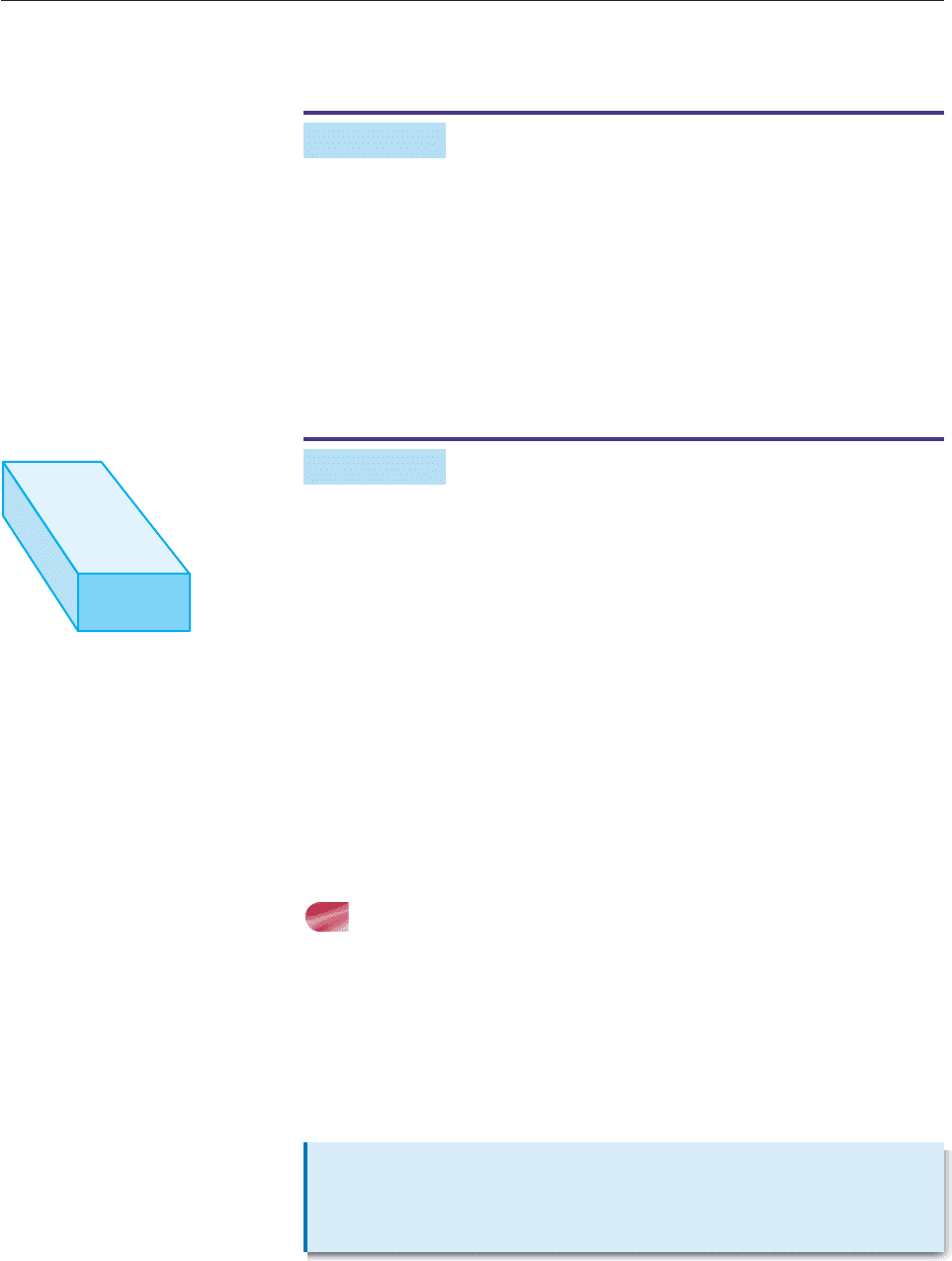
The surface area S of the rectangular box in Figure 1–9 is given by
2lh 2lw 2wh S.
Solve this equation for h.
SOLUTION Treat h as the variable and all the other letters as constants. First,
get all the terms involving the variable h on one side of the equation and every-
thing else on the other side.
2lh 2lw 2wh S
Subtract 2lw from both sides: 2lh 2wh S 2lw
Factor out h on the left side: (2l 2w)h S 2lw
Divide both sides by (2l 2w): h
S
2l
2
2
lw
w
. ■
QUADRATIC EQUATIONS
A second-degree, or quadratic, equation is an equation that can be written in the
form
ax
2
bx c 0
for some constants a, b, c, with a 0. There are several techniques for solving
such equations. We begin with the factoring method, which makes use of this
property of the real numbers:
20 CHAPTER 1 Basics
w
h
l
Figure 1–9
Zero
Products
If a product of real numbers is zero, then at least one of the factors is zero;
in other words,
If cd 0, then c 0 or d 0 (or both).

EXAMPLE 4
To solve 3x
2
x 10, we first rearrange the terms to make one side 0 and then
factor:
Subtract 10 from each side: 3x
2
x 10 0
Factor left side: (3x 5)(x 2) 0.
If a product of real numbers is 0, then at least one of the factors must be 0. So this
equation is equivalent to
3x 5 0orx 2 0
3x 5 x 2
x 5/3
Therefore the solutions are 5/3 and 2. ■
SECTION 1.2 Solving Equations Algebraically 21
There are two numbers whose square is 7, namely, 7
and 7
. So the solu-
tions of x
2
7 are 7
and 7
, or in abbreviated form, 7
. The same argu-
ment works for any positive real number d:
The solutions of x
2
d are d
and d
.
The same reasoning enables us to solve other equations.
EXAMPLE 5
Solve: (z 2)
2
5.
SOLUTION The equation says that z 2 is a number whose square is 5. Since
there are only two numbers whose square is 5, namely, 5
and 5
, we must
have
z 2 5
or z 2 5
z 5
2 z 5
2.
In compact notation, the solutions of the equation are 5
2. ■
CAUTION
You cannot use the factoring method unless one side of the equation is 0. Otherwise, you’ll get
the wrong answer, as is the case here:
x
2
3x 2 1
(x 2)(x 1) 1
x 2 1orx 1 1 Mistake here!
x
1or x 0
These are NOT solutions of the original equation, as you can easily verify.

We now use a slight variation of Example 5 to develop a method for solving
quadratic equations that don’t readily factor. Consider, for example, the expres-
sion x
2
6x. If you add 9, the result is a perfect square:
x
2
6x 9 (x 3)
2
.
The process of adding a constant to produce a perfect square is called comp-
leting the square. Note that one-half the coefficient of x in x
2
6x is
6
2
3. We
added 9, which is 3
2
, and the resulting perfect square was (x 3)
2
. The same idea
works in the general case, as is proved in Exercise 94.
22 CHAPTER 1 Basics
Completing
the Square
To change x
2
bx into a perfect square, add
b
2
2
. The resulting polynomial
x
2
bx
b
2
2
factors as
x
b
2
2
.
The following example shows how completing the square can be used to
solve quadratic equations.
EXAMPLE 6
To solve x
2
6x 1 0, we first rewrite the equation as x
2
6x 1. Next we
complete the square on the left side by adding the square of half the coefficient of x,
namely, (6/2)
2
9. To have an equivalent equation, we must add 9 to both sides:
x
2
6x 9 1 9
Factor left side: (x 3)
2
8.
Thus x 3 is a number whose square is 8. The only numbers whose squares equal
8 are 8
and 8
. So we must have
x 3 8
or x 3 8
x 8
3or x 8
3.
Therefore the solutions of the original equation are 8
3 and 8
3 or, in
more compact notation, 8
3. ■
We can use the completing-the-square method to solve any quadratic equation:*
ax
2
bx c 0
Divide both sides by a: x
2
b
a
x
a
c
0
Subtract
a
c
from both sides: x
2
b
a
x
a
c
*If you have trouble following any step here, do it for a numerical example, such as the case when
a 3, b 11, c 5.
CAUTION
Completing the square only works
when the coefficient of x
2
is 1. In an
equation such as
5x
2
x 2 0,
you must first divide every term on
both sides by 5 and then complete the
square.
Add
2
b
a
2
to both sides:
*
x
2
b
a
x
2
b
a
2
2
b
a
2
a
c
Factor left side:
x
2
b
a
2
2
b
a
2
a
c
Find common denominator
for right side:
x
2
b
a
2
4
b
a
2
2
a
c
b
2
4a
2
4ac
.
Since the square of x
2
b
a
equals
b
2
4a
2
4ac
, we must have
x
2
b
a
b
2
4a
2
4
ac
b
2
2
a
4
ac
Subtract
2
b
a
from
both sides:
x
2a
b
b
2
2
a
4
ac
b
2a
b
2
4
ac
.
We have proved
SECTION 1.2 Solving Equations Algebraically 23
*
This is the square of half the coefficient of x.
The Quadratic
Formula
The solutions of the quadratic equation ax
2
bx c 0 are
x
b
2a
b
2
4
ac
.
You should memorize the quadratic formula.
EXAMPLE 7
Solve x
2
3 8x.
SOLUTION Rewrite the equation as x
2
8x 3 0, and apply the quadratic
formula with a 1, b 8, and c 3:
x
b
2a
b
2
4
ac
8
2
52
8
2
213
4 13.
The equation has two distinct real solutions, 4 13 and 4 13. ■
8 4
13
2
8 4
13
2
8
8
2
4
1
3
2
1

EXAMPLE 8
Solve x
2
194x 9409 0.
SOLUTION Use a calculator and the quadratic formula with a 1, b 194,
and c 9409:
x
b
2a
b
2
4
ac
194
2
0
97.
Thus, 97 is the only solution of the equation. ■
EXAMPLE 9
Solve 2x
2
x 3 0.
SOLUTION Use the quadratic formula with a 2, b 1, and c 3:
x
b
2a
b
2
4
ac
1
4
1 24
1
4
23
.
Since 23
is not a real number, this equation has no real solutions (that is, no
solutions in the real number system). ■
The expression b
2
4 ac in the quadratic formula is called the discriminant.
As the last three examples illustrate, the discriminant determines the number of
real solutions of the equation ax
2
bx c 0.
1
1
2
4
2
3
2
2
194 37636
376
36
2
(194)
(194
)
2
4
1
9409
2
1
24 CHAPTER 1 Basics
Real Solutions of a
Quadratic Equation
Number of
Discriminant Real Solutions
b
2
4ac of ax
2
bx c 0 Example
0 Two distinct real solutions Example 7
0 One real solution Example 8
0 No real solutions Example 9
EXAMPLE 10
Use the discriminant to determine the number of real solutions of each of these
equations.
(a) 4x
2
20x 25 0 (b) 7x
2
3 5x (c) .5x
2
6x 2 0.

SOLUTION
(a) Here a 4, b 20, and c 25. So the discriminant is
b
2
4ac (20)
2
4 4 25 400 400 0.
The equation has one real solution.
(b) First rewrite the equation as 7x
2
5x 3 0. The discriminant is
b
2
4ac (5)
2
4 7 3 25 84 59,
so the equation has no real solutions.
(c) The discriminant is b
2
4ac 6
2
4 (.5) (2) 36 4 40. There
are two real solutions. ■
The quadratic formula and a calculator can be used to solve any quadratic
equation with nonnegative discriminant.
EXAMPLE 11
The number of identity theft complaints (in thousands) in year x is approxi-
mated by
5.5x
2
77.1x 26.3 (0 x 9),
where x is the number of years since 2000.* Use the quadratic formula and a cal-
culator to find the year in which there were 247,000 complaints.
SOLUTION Complaints are measured in thousands, so we must solve
5.5x
2
77.1x 26.3 247.
Subtracting 247 from both sides produces the equivalent equation
5.5x
2
77.1x 220.7 0.
To solve this equation, we compute the radical part of the quadratic formula
b
2
4
ac
77.1
2
4(5.
5)(22
0.7)
and store the result in memory D. By the quadratic formula, the solutions of the
equation are
x
b
2
a
D
2
7
(
7
.1
5
.5)
D
.
So the approximate solutions are
x
2
7
(
7
.1
5
.5)
D
4.009 and x
2
7
(
7
.1
5
.5)
D
10.009,
as shown in Figure 1–10. Since we are given that 0 x 9, the only applicable
solution here is x 4.009, which corresponds to early 2004. ■
b
b
2
4
ac
2a
SECTION 1.2 Solving Equations Algebraically 25
Figure 1–10
*Based on data from the Identity Theft Clearinghouse of the Federal Trade Commission.
