Hungerford T.W., Shaw D.J. Contemporary Precalculus: A Graphing Approach
Подождите немного. Документ загружается.

76
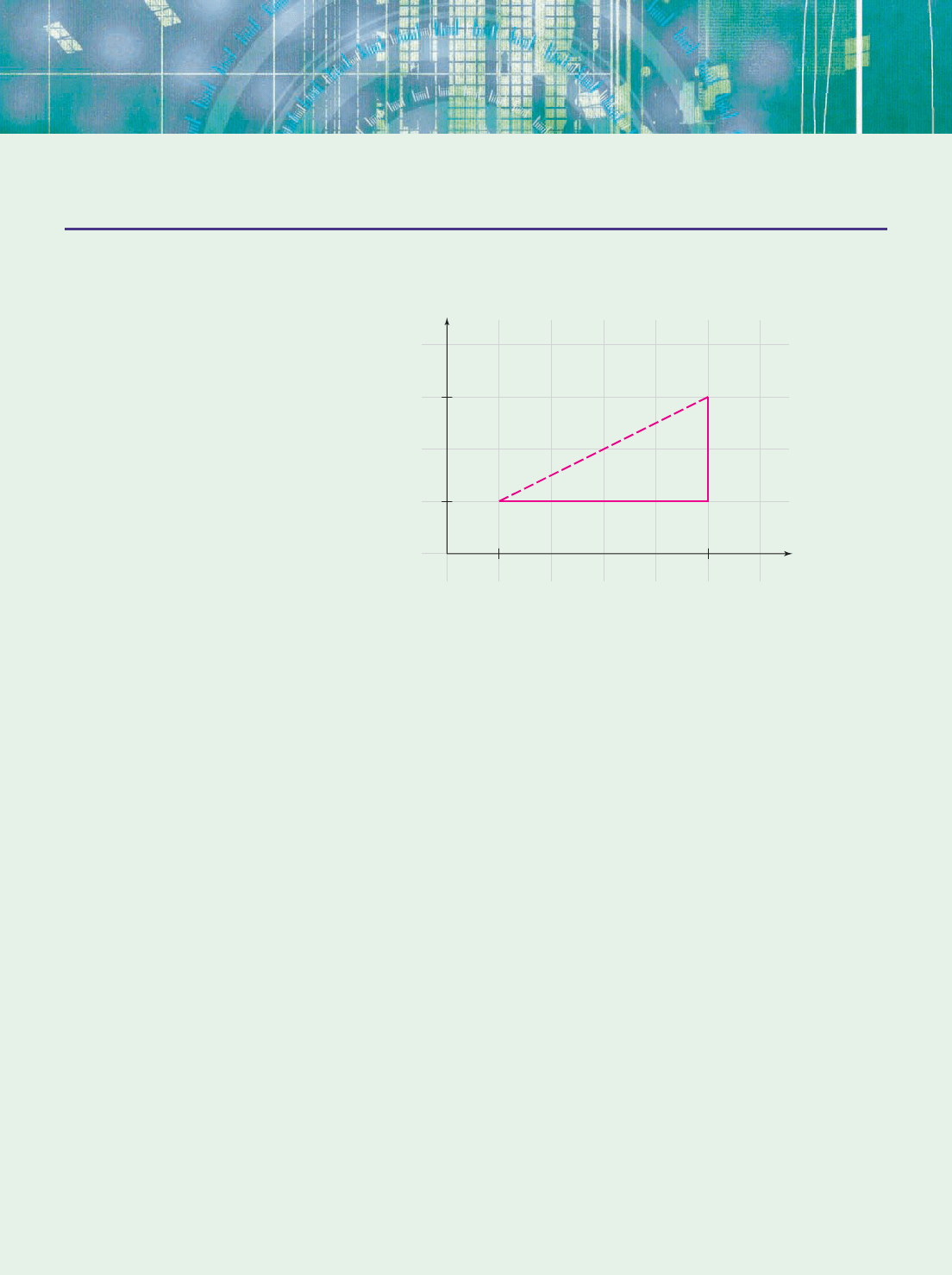
More generally, suppose A and B have coordinates (x
1
, y
1
) and (x
2
, y
2
) respec-
tively. Then Figure 2 shows that u x
2
x
1
and v y
2
y
1
(why?).
Figure 2
Therefore, the taxicab distance formula is
Taxicab distance from (x
1
, y
1
) to (x
2
, y
2
) x
2
x
1
y
2
y
1
.
The taxicab circle with center (a,b) and radius r consists of all points (x,y) whose
taxicab distance from (a, b)isr. Substituting (a, b) and (x, y) for (x
1
, y
1
) and (x
2
, y
2
)in
the taxicab distance formula, we see that the equation of this taxicab circle is
r x a y b, or equivalently, x a y b r.
Find the equations of these taxicab circles:
4. Center (0, 0), radius 4
5. Center (0, 0), radius 1000
6. Center (3, 4), radius 5
According to the equations above, the taxicab unit circle (center at (0, 0), ra-
dius 1) is the graph of
x 0 y 0 1, that is, x y 1.
7. Graph the taxicab unit circle. [Hint: You can plot points, but it’s better to
find the graph one quadrant at a time. Use the definition of absolute
value to rewrite the equation for each of the four quadrants. In quadrant I,
x 0 and y 0, so the equation is x y 1. In quadrant II, x 0 and
y 0 so the equation is (x) y 1, and so on.]
Suppose the drug dealer in the first paragraph of this project is standing at the origin.
8. Graph the taxicab circle of radius 1000 with the drug dealer as center.
9. On the same coordinate plane as in Exercise 8, graph the ordinary circle
of radius 1000 with the drug dealer as center.
B(x
2
, y
2
)
A(x
1
, y
1
)
(x
2
, y
1
)
u
v
x
y
y
1
x
1
x
2
y
2
DISCOVERY PROJECT 1

77
GRAPHS AND TECHNOLOGY
Are the financial rewards worth it?
Data from past years shows that the typical college
graduate earned more than the typical high school
graduate (with no college). Technology can be used to
construct a linear model to estimate the median
earnings of both groups of graduates in future years
and to determine whether the gap between the two
groups is increasing or decreasing. See Exercises 20
and 21 on page 130.
77
Chapter
© Barry Austin Photography/Getty Images
FPO
1200
−1
0
12

78
y
x
1
(0, 0)
(.5, .25)
(1, 1)
(1.5, 2.25)
(2.5, 6.25)
(2, 4)
234
1
2
3
4
5
6
7
8
−1−2−3−4
Figure 2–1
xy x
2
2.5 6.25
24
1.5 2.25
11
.5 .25
00
.5 .25
11
1.5 2.25
24
2.5 6.25
y
x
12
y = x
2
34
1
2
3
4
5
6
7
8
−1−2−3−4
Figure 2–2
Chapter Outline
Interdependence of
Sections
2.1 Graphs
2.2 Solving Equations Graphically and Numerically
2.3 Applications of Equations
2.4 Optimization Applications
2.5 Linear Models
Technology for graphing, solving equations, and building mathematical
models is introduced in this chapter. It is a powerful tool for dealing with
complicated mathematical situations and real-world problems that might
otherwise be intractable. Keep in mind, however, that technology is not a
substitute for mathematical knowledge or common sense. To use it effec-
tively, you need a sound grounding in algebra and geometry.
2.1 2.2 2.3 2.4
2.5
2.1 Graphs
■ Graph an equation by plotting points.
■ Graph an equation using technology.
■ Use the graphing tools available with graphing technology.
■ Use technology to create a scatter plot and line graph.
The traditional method of graphing an equation “by hand” is as follows: Construct
a table of values with a reasonable number of entries, plot the corresponding
points, and use whatever algebraic or other information is available to make an
educated guess about the rest.
EXAMPLE 1
The graph of y x
2
consists of all points (x, x
2
), where x is a real number. You can
easily construct a table of values and plot the corresponding points, as in Figure 2–1.
Section Objectives
SECTION 2.1 Graphs 79
These points suggest that the graph looks like the one in Figure 2–2, which is
obtained by connecting the plotted points and extending the graph upward. ■
GRAPHING WITH TECHNOLOGY
Graphing calculators and computer graphing programs use no algebraic reasoning
when sketching graphs. They plot 95 or more points and simultaneously connect
them with line segments. These graphs are generally quite accurate, but no tech-
nology is perfect. Algebra and geometry may be needed to interpret misleading or
incorrect screen images. The basic procedure for graphing with technology is
summarized in the following box and explained in Example 2 below.
Graphing Equations
with Technology
1. Solve the equation for y and enter it in the equation memory.
2. Set the viewing window—the portion of the coordinate plane that will
appear on the screen.
3. Graph the equation.
4. If necessary, adjust the viewing window for a better view.
EXAMPLE 2
Graph the equation
2x
3
8x 2y 4 0
(a) using a calculator;
(b) using a computer graphing program.
SOLUTION
(a) For calculator graphing, use the four steps in the preceding box.
Step 1 Solve the equation for y:
2x
3
8x 2y 4 0
Rearrange terms: 2y 2x
3
8x 4
Divide by 2: y x
3
4x 2.
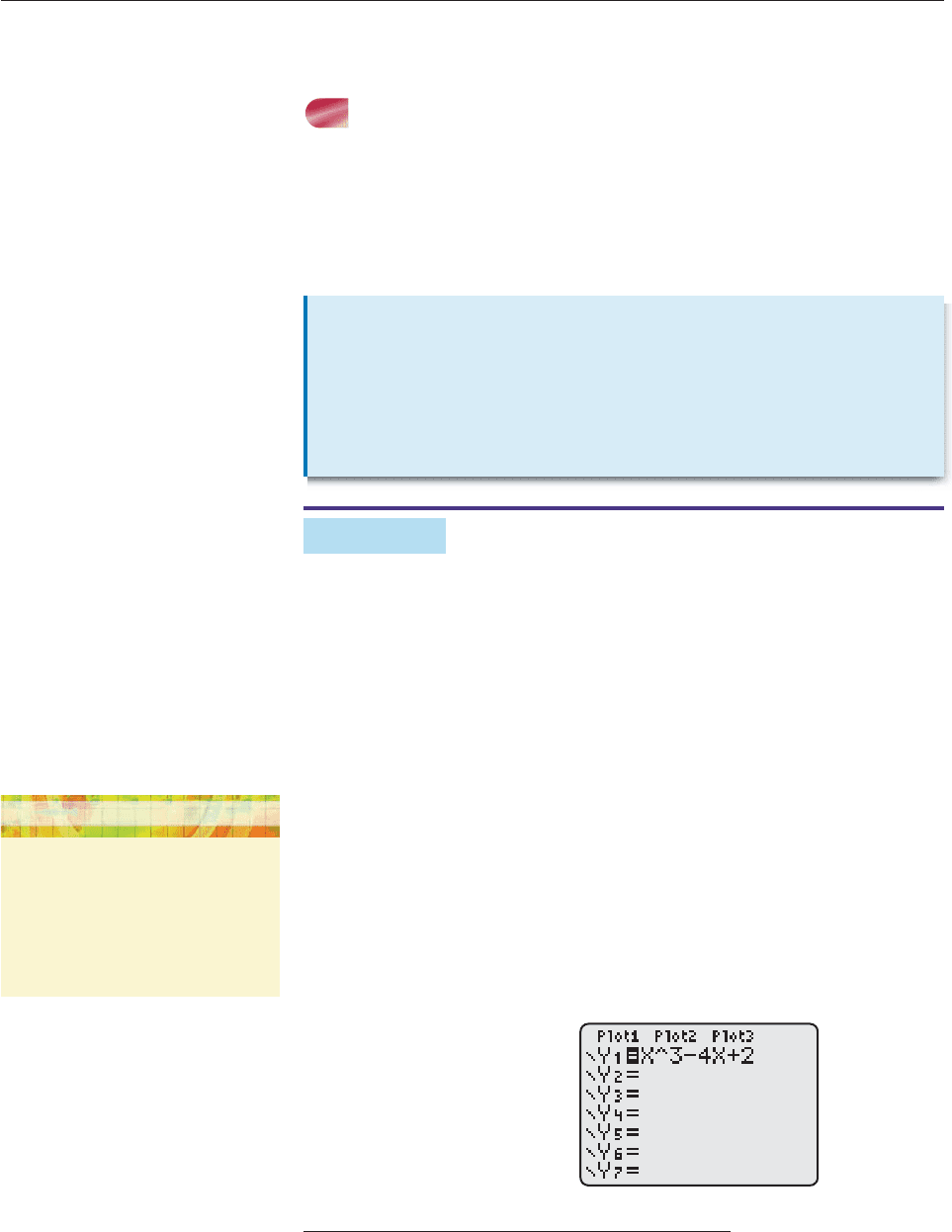
Now call up the equation memory by pressing Y on TI (or
SYMB on HP-39gs or GRAPH (main menu) on Casio).* Use the
Technology Tip in the margin to enter the equation, as shown in
Figure 2–3.
Figure 2–3
*On TI-86, press GRAPH first, then y(x) will appear as a menu choice.
TECHNOLOGY TIP
When entering an equation for graph-
ing, use the “variable” key rather than
the ALPHA X key. It has a label such as
X, T, u or X, T, u, n or X, u, T or x-VAR.
On TI-89, however, use the x key on the
keyboard.
80 CHAPTER 2 Graphs and Technology
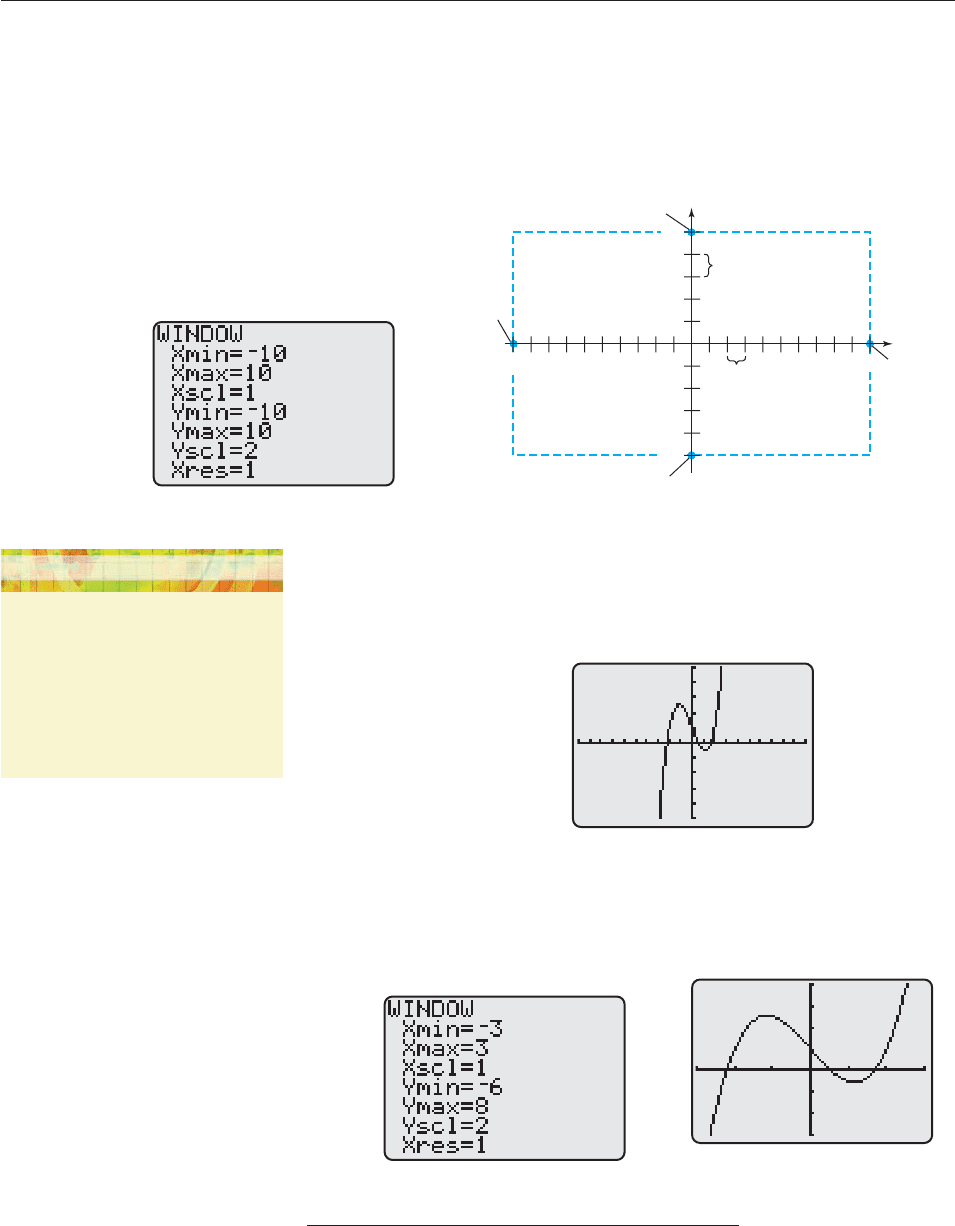
Step 2 Since we don’t know where the graph lies, we’ll use the standard
window—the one with 10 x 10 and 10 y 10. We can
change it later if necessary. Press WINDOW or WIND on TI (or
V-WINDOW on Casio or PLOT SETUP on HP), and enter the
appropriate numbers, as in Figure 2–4. Figure 2–5 shows how
these entries determine the portion of the plane to be shown and
the placement of axis tick marks.*
Figure 2–4
y
x
x min
x max
Yscl = 2
Xscl = 1
y max
y min
510
4
−2
−6
−4
−8
−10
8
2
6
10
−5−10
Figure 2–5
Step 3 Press GRAPH on TI (or DRAW on Casio or PLOT on HP) to ob-
tain Figure 2–6. Because of the limited resolution of a calculator
screen, the graph appears to consist of short adjacent line segments
rather than a smooth unbroken curve.
10
−10
−10 10
Figure 2–6
Step 4 The graph in Figure 2–6 is squeezed into the middle of the screen.
So we change the viewing window (Figure 2–7) and press GRAPH
again to obtain Figure 2–8.
*Xscl is labeled “X scale” on Casio and “Xtick” on HP-39gs. Xres should normally be set at 1 on TI
and “res” should normally be set at “detail” on HP. Casio has no resolution setting.
Figure 2–7
8
−6
−33
Figure 2–8
TECHNOLOGY TIP
On TI-83/86 you may get an error mes-
sage when you press GRAPH if one of
Plot 1, Plot 2, or Plot 3, at the top of
the Y menu (see Figure 2–3) is
shaded. In this case, move the cursor
over the shading and press ENTER to
remove it.
SECTION 2.1 Graphs 81
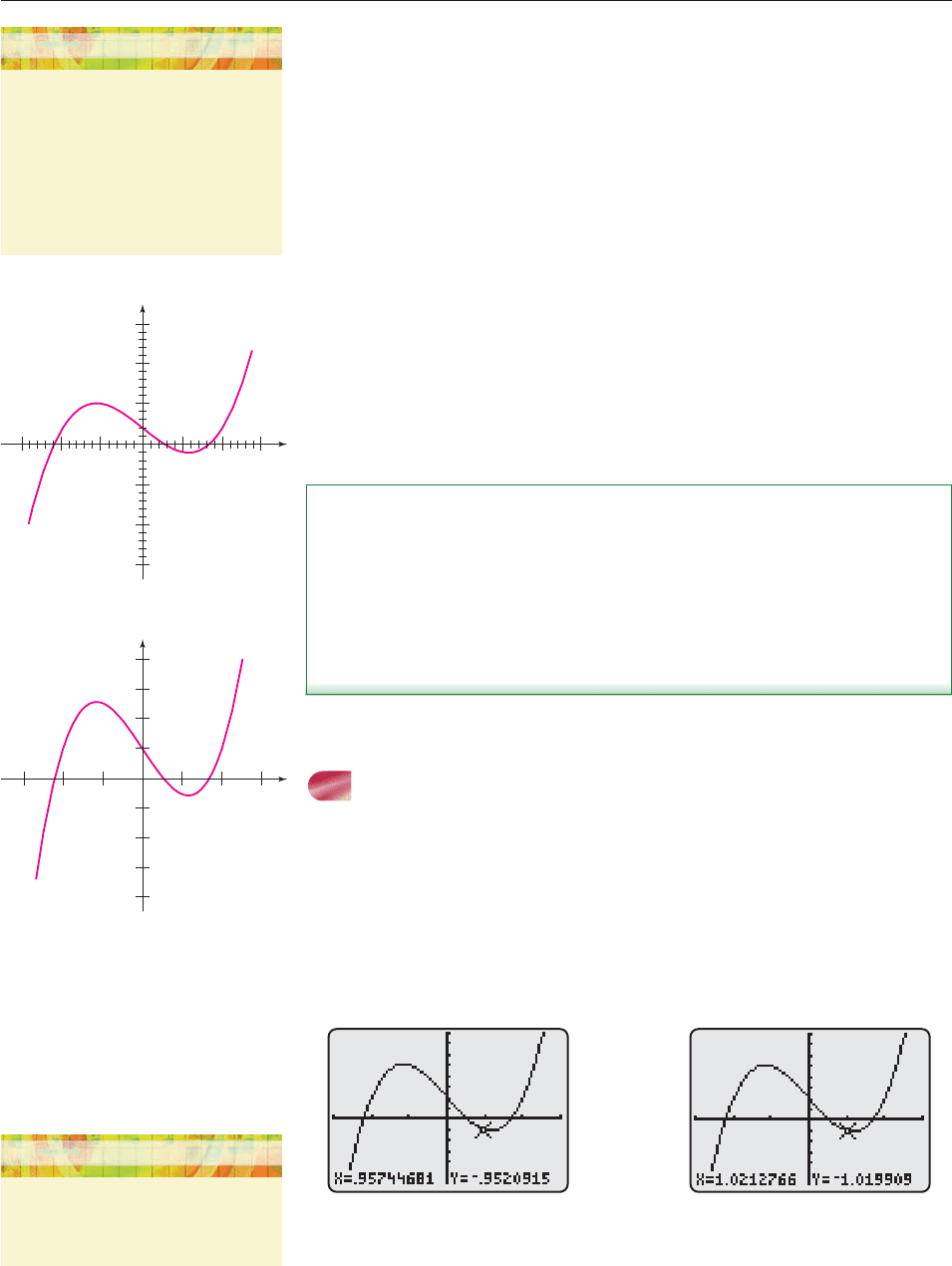
(b) The procedure for a typical computer graphing program is basically the same
as for calculators, but various details may be a bit different. So check your in-
struction manual or help key index. On Maple, for example, the following
command produces Figure 2–9, in which the range of y-values was chosen
automatically by Maple.
plot(x^3 4*x 2, x 3..3);
To duplicate Figure 2–8, we specify the range of y-values and the number of
tick marks on each axis:
plot(x^3 4*x 2, x 3..3, y 6..8,
xtickmarks 6, ytickmarks 6);
The result is Figure 2–10.
As is typical of computer-generated graphs, this one appears smooth and
connected, as it should. ■
5
−1
1
2
3−2−3
−10
−15
−5
10
15
x
y
Figure 2–9
4
2
−1123−2−3
−2
−6
−8
−4
6
8
x
y
Figure 2–10
GRAPHING TOOLS: THE TRACE FEATURE
A calculator obtains a graph by plotting points and simultaneously connecting
them. To see which points were actually plotted, press TRACE, and a flashing
cursor appears on the graph. Use the left and right arrow keys to move the cursor
along the graph. The coordinates of the point the cursor is on appear at the bottom
of the screen. Figure 2–11 illustrates this for the graph of y x
3
4x 2.
8
−6
(a)
−33
8
−6
(b)
−33
Figure 2–11
TECHNOLOGY TIP
Most calculators understand “implied
multiplication” (for instance, that
4x means 4 x), but some computer
graphing programs do not. If we had
typed in 4x in Example 2(b) instead of
4*x we would have gotten an error mes-
sage in MAPLE, but not in Mathematica.
TECHNOLOGY TIP
If TRACE is not on the keyboard, it will
appear on screen after you press
GRAPH (or PLOT or DRAW).
NOTE
An equation stays in a calculator’s equation memory until you delete it. When several equations are
in the memory, you must turn “on” those you want graphed and turn “off” those you don’t want
graphed. An equation is “on” if its equal sign is shaded or if there is a check mark next to it. Only
equations that are “on” are graphed when you press GRAPH. To turn an equation “on” or “off” on
TI-84+, move the cursor over the equal sign and press ENTER. On other calculators, move the cur-
sor to the equation and press SELECT or CHECK.

The trace cursor displays only the points that the calculator actually plotted. For
instance, (1, 1) is on the graph of y x
3
4x 2, as you can easily verify, but
was not one of the points the calculator plotted to produce Figure 2–11. So the
trace lands on two nearby points that were plotted, but skips (1, 1).
GRAPHING TOOLS: ZOOM IN/OUT
The ZOOM menu makes it easy to change the size of the viewing window.
EXAMPLE 3
How many x-intercepts does the graph of y x
3
1.8x .97 have between 5
and 5?
SOLUTION The graph of this equation in Figure 2–12 suggests that there is one
x-intercept near 1.5 and another one between 0 and 1. But appearances can be
deceiving. Use the Technology Tip in the margin to set the zoom factors at 10, then
move the cursor to the apparent positive x-intercept. Choose Zoom In in the ZOOM
menu and press ENTER. The result is Figure 2–13, which shows clearly that the
graph does not touch the x-axis there. So there is only one x-intercept. ■
82 CHAPTER 2 Graphs and Technology
5
3
3
5
.245
.3
.3
1.245
Figure 2–12
Figure 2–13
The calculator automatically changes the range of x- and y-values when
zooming, but does not change the Xscl or Yscl settings. This may cause occasional
viewing problems.
NOTE
The heading GRAPHING EXPLORATION
indicates that you are to use your cal-
culator or computer as directed to com-
plete the discussion.
GRAPHING TOOLS: SPECIAL VIEWING WINDOWS
On most calculators, frequently used viewing windows can be obtained with a
single keystroke. These include the following.
1. The standard viewing window has 10 x 10 and 10 y 10. It
is labeled ZStandard, ZStd, or ZoomStd in the ZOOM menu on TI, and Std
in the V-WINDOW menu on Casio.
TECHNOLOGY TIP
If ZOOM is not on the keyboard, it will
appear on screen after you press
GRAPH (or PLOT or DRAW).
To set the zoom factors, look for
Fact, ZFact, or (Set) Factors in the
ZOOM menu (or its MEMORY submenu).
Graph y x
3
1.8x .97 in the same window as Figure 2–12. Then zoom out
from the origin by a factor of 10. Can you read the tick marks on the axes? Change
the settings to Xscl 5 and Yscl 5, and regraph. Can you read them now?
GRAPHING EXPLORATION
2. A decimal window is one in which the horizontal distance between two
adjacent pixels is .1. The width of a decimal window depends on the
width of your calculator screen. To find this width, call up the preset
decimal window (see the Technology Tip) and look in WINDOW. For
example, the preset decimal window in the TI-84+ has 4.7 x 4.7,
so its width is 4.7 (4.7) 9.4. Consequently, any TI-84 window
with Xmax Xmin 9.4 (such as 0 x 9.4 or 5 x 14.4) is a
decimal window.
SECTION 2.1 Graphs 83
3. In a square window, a one-unit segment on the x-axis has the same length
on the screen as a one-unit segment on the y-axis. Because calculator
screens are wider than they are high, the y-axis in a square window must
be shorter than the x-axis (see the Technology Tip in the margin).
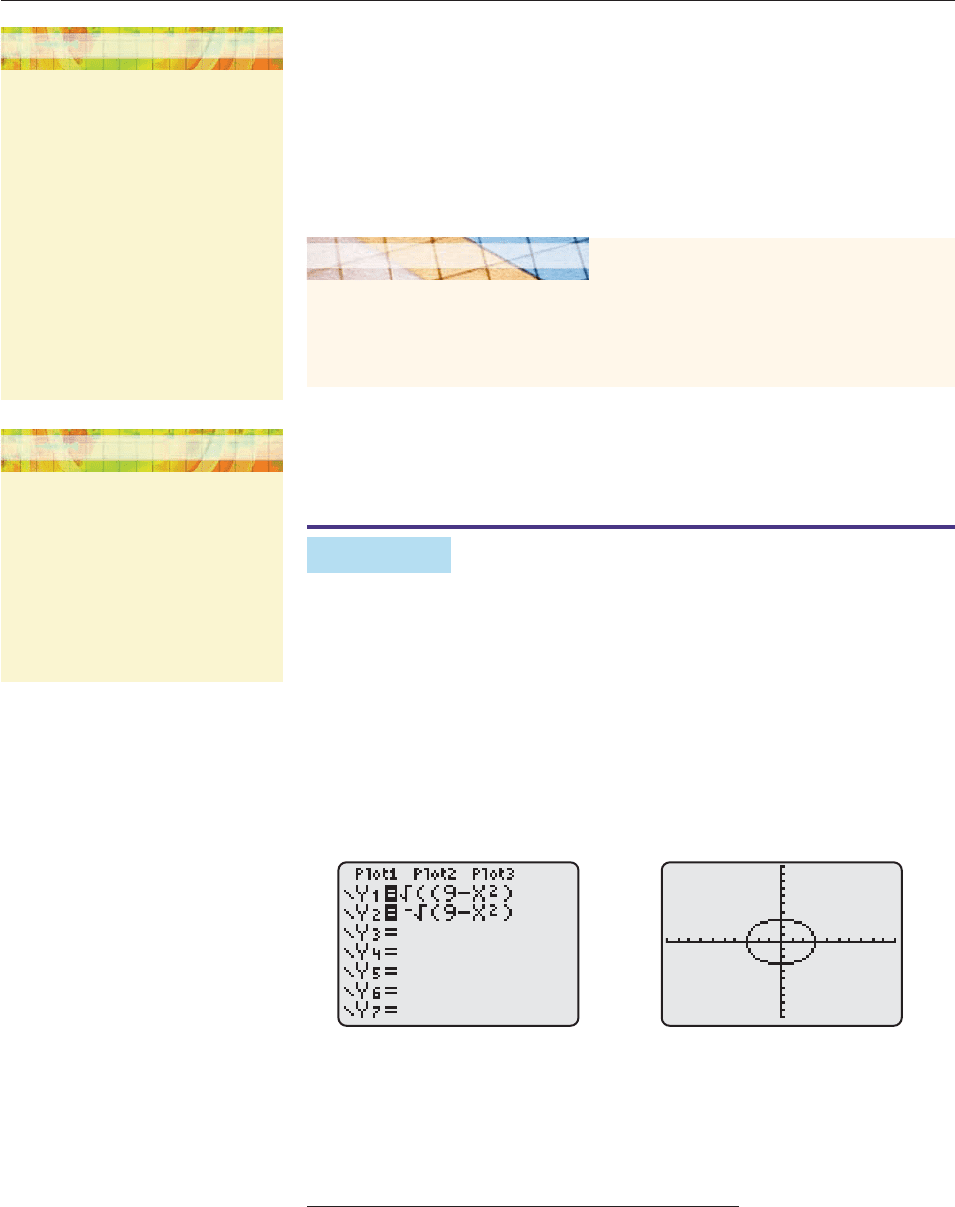
EXAMPLE 4
Graph the circle x
2
y
2
9 on a calculator.
SOLUTION First, we solve the equation for y:
y
2
9 x
2
y 9 x
2
or y 9 x
2
.
Graphing both of these equations on the same screen will produce the graph of the
circle (Figure 2–14). However, the graph does not look like a circle because the
standard window in Figure 2–14 is not square (a one-unit segment on the x-axis is
a tad longer than a one-unit segment on the y-axis).
10
−10
−10 10
Figure 2–14
If we select Square (or ZSquare, ZSqr, ZoomSqr, or Sqr) in the ZOOM menu, the
length of the x-axis is adjusted to produce a square window in which the circle looks
round (Figure 2–15 on the next page).* Alternatively, we can change the WINDOW
settings by hand to obtain a square window such as Figure 2–16.
†
■
*On HP-39gs, SQUARE adjusts the length of the y-axis to produce a square window.
†
The gap between the top and bottom of the circle (more apparent here than in Figure 2–15) is caused
by the low resolution of the calculator screen.
TECHNOLOGY TIP
For a decimal window in which both
the horizontal and vertical distance
between adjacent pixels is .1, use this
menu/choice
TI-84+: ZOOM/Zdecimal
TI-86: ZOOM/Zdecm
TI-89: ZOOM/ZoomDec
Casio 9850: V-WINDOW/Init
HP-39gs: ZOOM/Decimal
On these windows you may need to
change the Ymin and Ymax settings to
get the full picture.
TECHNOLOGY TIP
For an approximately square window,
the y-axis should be 2/3 as long as the
x-axis on TI-84 and 3/5 as long on
TI-86. It should be half as long on
TI-89, Casio, and HP-39gs.
On calculators other than TI-86,
the decimal window is a square
window.
Graph y x
4
2x
2
2 in the standard window. Use the TRACE key, and watch
the values of the x-coordinates. Now regraph in a decimal window (use the Technol-
ogy Tip). Then use the TRACE key again. How do the x-coordinates change at each
step? Finally, look in WINDOW to find the width of your decimal window.
GRAPHING EXPLORATION
Although any convenient viewing window is usually OK, you should use a
square window when you want circles to look round and perpendicular lines to
look perpendicular.
84 CHAPTER 2 Graphs and Technology
15.16
10
.10
15.16
6
4
4
6
Figure 2–15
Figure 2–16
The method used to graph the circle x
2
y
2
9 in Example 4 can be used to
graph any equation that can be solved for y.
EXAMPLE 5
To graph 12x
2
4y
2
16x 12 0, solve the equation for y:
4y
2
12x
2
16x 12
y
2
3x
2
4x 3
y 3x
2
4x 3
.
Every point on the graph of the equation is on the graph of either
y 3x
2
4x 3
or y 3x
2
4x 3
.
GRAPHING TOOLS: THE MAXIMUM/MINIMUM FINDER
Many graphs have peaks and valleys (for instance, see Figure 2–12 on page 82 or
Figure 2–17 on the next page). A calculator’s maximum finder or minimum finder
can locate these points with a high degree of accuracy, as illustrated in the next
example.
The lines y .5x and y 2x 2 are perpendicular (why?). Graph them in the
standard viewing window. Do they look perpendicular? Now graph them in a square
window. Do they look perpendicular?
GRAPHING EXPLORATION
Graph the previous two equations on the same screen. The result will be the graph of
the original equation.
■
GRAPHING EXPLORATION
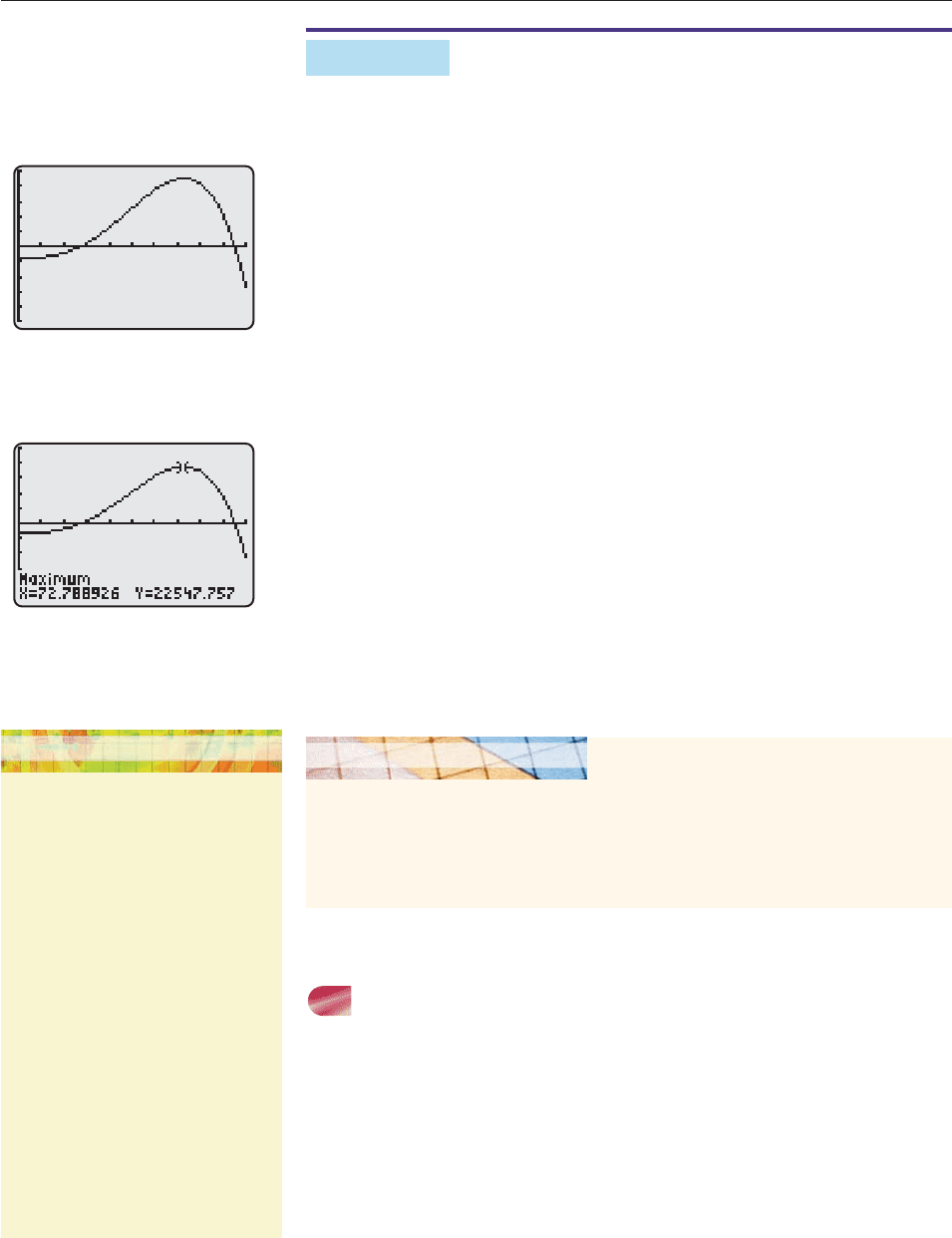
EXAMPLE 6
The Cortopassi Computer Company can produce a maximum of 100,000 com-
puters a year. Their annual profit is given by
y .003x
4
.3x
3
x
2
5x 4000,
where y is the profit (in thousands of dollars) from selling x thousand computers.
Use graphical methods to estimate how many computers should be sold to make
the largest possible profit.
SOLUTION We first choose a viewing window. The number x of computers is
nonnegative, and no more than 100,000 can be produced, so that 0 x 100
(because x is measured in thousands). The profit y may be positive or negative (the
company could lose money). So we try a window with 25,000 y 25,000
and obtain Figure 2–17. For each point on the graph,
The x-coordinate is the number of thousands of computers produced;
The y-coordinate is the profit (in thousands) on that number of computers.
The largest possible profit occurs at the point with the largest y-coordinate, that is,
the highest point in the window. The maximum finder on a TI-84+ (see the Tech-
nology Tip in the margin) produced Figure 2–18. Since x and y are measured in
thousands, we see that making about 72,789 computers results in a maximum
profit of about $22,547,757. ■
SECTION 2.1 Graphs 85
25,000
−25,000
0 100
Figure 2–17
25,000
−25,000
0 100
Figure 2–18
COMPLETE GRAPHS
A viewing window is said to display a complete graph if it shows all the impor-
tant features of the graph (peaks, valleys, intercepts, etc.) and suggests the general
shape of the portions of the graph that aren’t in the window. Many different win-
dows may show a complete graph. It’s usually best to use a window that is small
enough to show as much detail as possible.
In later chapters we shall develop algebraic facts that will enable us to know
when certain graphs are complete. For the present, however, the best you may be
able to do is try several different windows to see which, if any, appear to display
a complete graph.
Graph y .3x
3
.8x
2
2x 1 in the window with 5 x 5 and 5 y 5.
Use your maximum finder to approximate the coordinates of the highest point to the
left of the y-axis. Then use your minimum finder (in the same menu) to approximate
the coordinates of the lowest point to the right of the y-axis. How do these answers
compare with the ones you get by using the trace feature?
GRAPHING EXPLORATION
TECHNOLOGY TIP
The graphical maximum finder is in
the following menu/submenu:
TI-84+: CALC
TI-86/89: GRAPH/MATH
Casio: GRAPH/G-SOLVE
HP-39gs: PLOT/FNC
It is labeled Maximum, Max, FMax, or
Extremum.
On some TI calculators, you
must first select a left (or lower)
bound, meaning an x-value to the left
of the highest point, and a right (or
upper) bound, meaning an x-value to
its right, and make an initial guess.
On other calculators, you may have to
move the cursor near the point you
are seeking.
