Hungerford T.W., Shaw D.J. Contemporary Precalculus: A Graphing Approach
Подождите немного. Документ загружается.

SOLUTION First draw a sketch of the situation and labels the sides of the gar-
den as in Figure 2–52.
116 CHAPTER 2 Graphs and Technology
For the parallel sides, she needs 2x feet of fencing at $4 per foot. For the side
opposite the river, she needs z feet of fencing at $18 per foot. So her cost is
C 2x(4) z(18) 8x 18z.
We must find the values of x and z that make C as small as possible. We begin by
expressing C in terms of a single variable. The garden is to have an area of 10,000
square feet and the area of a rectangle is its length times its width. So
xz area 10,000
z
10,
x
000
.
Substituting this expression for z in the cost equation, we obtain
C 8x 18z
C 8x 18
10,
x
000
C 8x
180
x
,000
.
Now graph y 8x
180
x
,000
(Figure 2–53). If (x, y) is a point on the graph, then
x represents the side length of the garden;
y represents the cost of fencing a garden with this side length.
To find the minimum cost we use a minimum finder to determine the lowest point
on the graph (that is, the one with the smallest y-coordinate), as in Figure 2–54.
Therefore, the minimum cost is $2400 and the garden with this minimum cost has
dimensions
x 150 ft and z
10,
x
000
10
1
,
5
0
0
00
66
2
3
ft. ■
4000
0
1000
300
Figure 2–53
4000
0
1000
300
Figure 2–54
xx
z
Figure 2–52
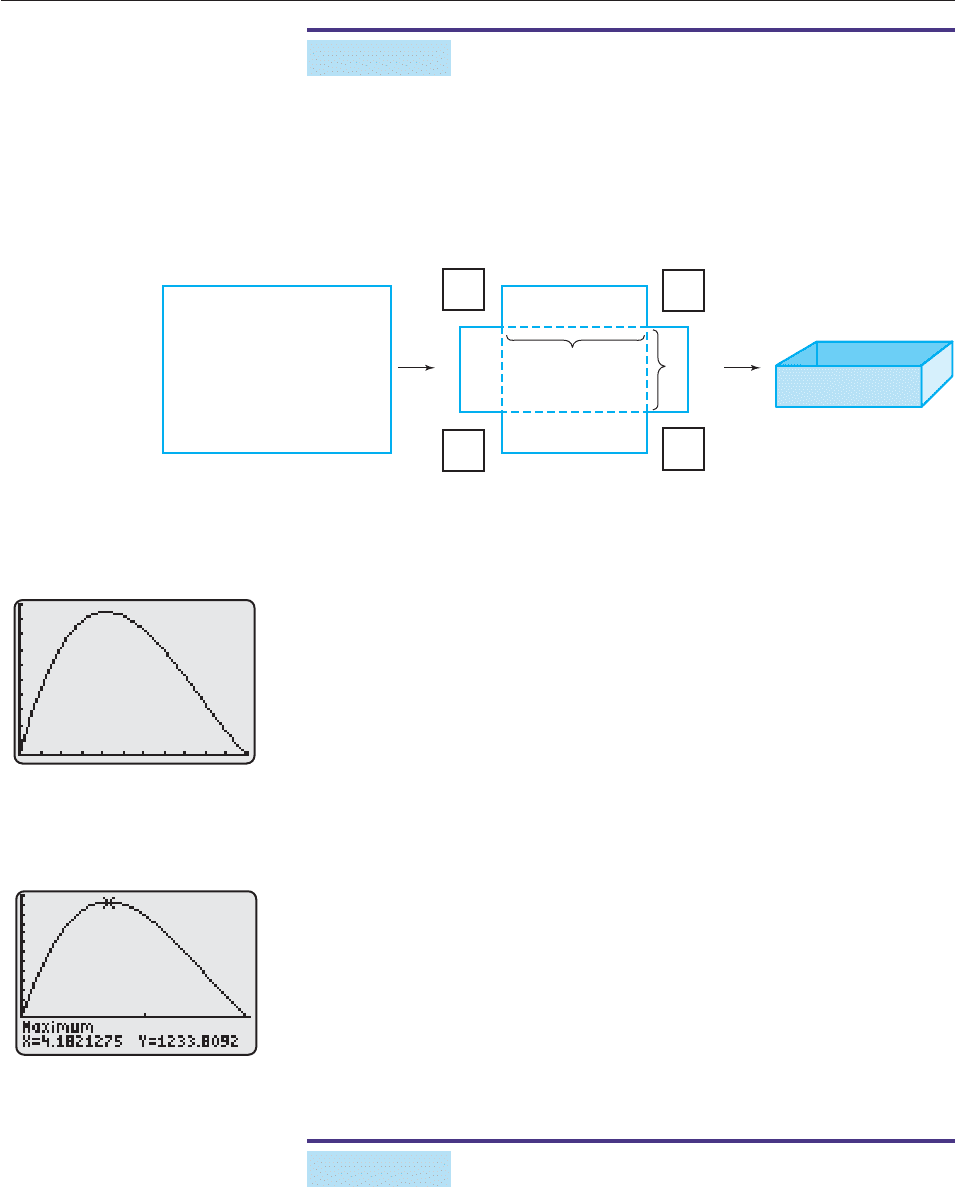
EXAMPLE 3
A box with no top is to be made from a 22 30 inch sheet of cardboard by cut-
ting squares of equal size from each corner and bending up the flaps, as shown in
Figure 2–55. To the nearest hundredth of an inch, what size square should be cut
from each corner in order to obtain a box with the largest possible volume, and
what is the volume of this box?
Figure 2–55
SOLUTION Let x denote the length of the side of the square to be cut from
each corner. Then, as we saw in Example 10 of Section 2.3 (page 109),
Volume of box Length Width Height
(30 2x)
(22 2x)
x
4x
3
104x
2
660x.
Thus, the equation y 4x
3
104x
2
660x gives the volume y of the box that
results from cutting a square of side x from each corner. Since the shortest side of
the cardboard is 22 inches, the length x of the side of the cut-out square must be
less than 11 (why?).
Each point on the graph of y 4x
3
104x
2
660x (0 x 11) in Fig-
ure 2–56 represents one of the possibilities:
The x-coordinate is the size of the square to be cut from each corner;
The y-coordinate is the volume of the resulting box.
The box with the largest volume corresponds to the point with the largest
y-coordinate, that is, the highest point in the viewing window. A maximum finder
(Figure 2–57) shows that this point is approximately (4.182, 1233.809). Therefore,
a square measuring approximately 4.18 4.18 inches should be cut from each
corner, producing a box of volume approximately 1233.81 cubic inches. ■
EXAMPLE 4
A cylindrical can of volume 58 cubic inches (approximately 1 quart) is to be
designed. For convenient handling, it must be at least 1 inch high and 2 inches in
diameter. What dimensions will use the least amount of material?
22
30
30 − 2x
xx
x
x
22 − 2x
SECTION 2.4 Optimization Applications 117
——
——
——
1300
0
0
11
Figure 2–56
1300
011
Figure 2–57
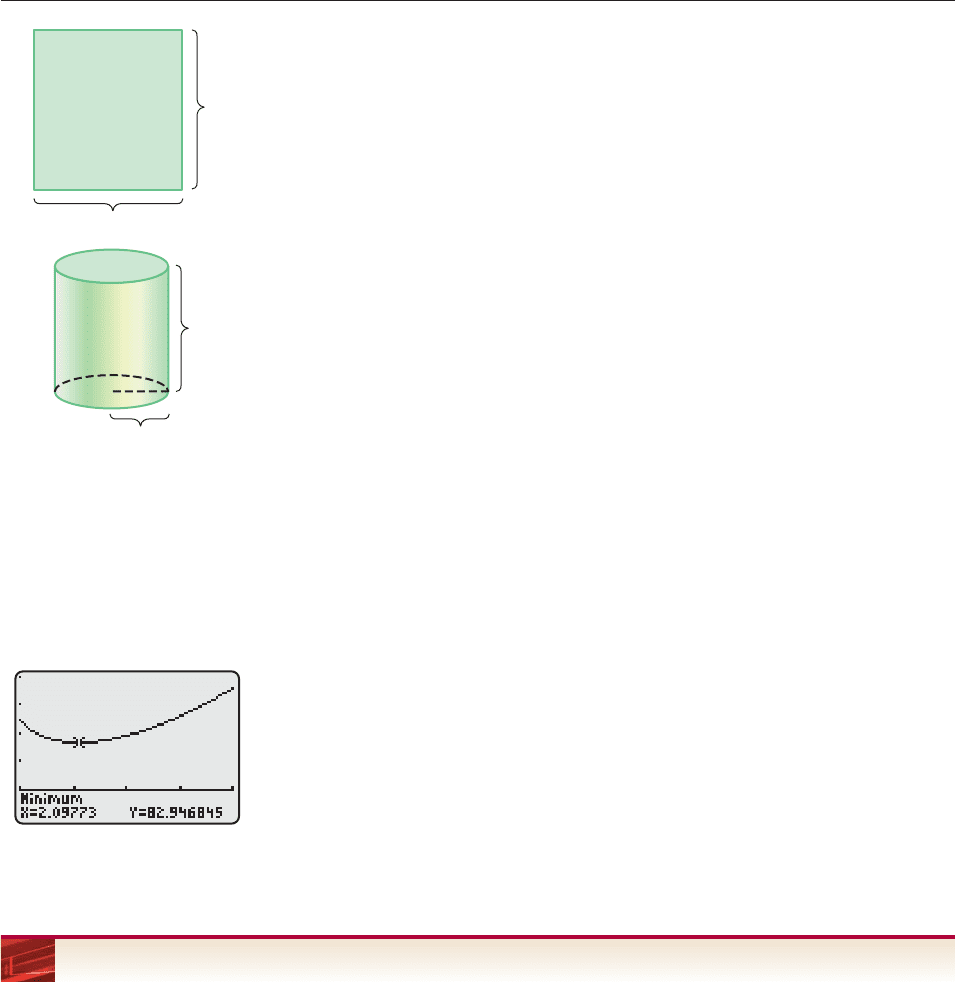
SOLUTION We can construct a can by rolling a rectangular sheet of metal into
a tube and then attaching the top and bottom, as shown in Figure 2–58. The sur-
face area of the can (which determines the amount of material) is
Area of rectangular Area of Area of
sheet top bottom
ch pr
2
pr
2
ch 2pr
2
.
When the sheet is rolled into a tube, the width c of the sheet is the circumference
of the end of the can, so that c 2pr, and hence,
Surface area ch 2pr
2
2prh 2pr
2
.
The volume of a cylinder of radius r and height h is pr
2
h. Since the can is to have
volume 58 cubic inches, we have
pr
2
h 58, or equivalently, h
p
5
r
8
2
.
Therefore,
Surface area 2prh 2pr
2
2pr
p
5
r
8
2
2pr
2
11
r
6
2pr
2
.
Note that r must be greater than 1 (since the diameter 2r must be at least 2). Fur-
thermore, r cannot be more than 5 (if r 5 and h 1, then the volume pr
2
h
would be at least p
25
1, which is greater than 58).
The situation can be represented by the graph of the equation
y 116/x 2px
2
,
as in Figure 2–59. The x-coordinate of each point represents a possible radius, and
the y-coordinate represents the surface area of the corresponding can. We must
find the point with the smallest y-coordinate, that is, the lowest point on the graph.
A graphical minimum finder (Figure 2–59) shows that the coordinates of this
point are approximately (2.09773, 82.946845). If the radius is 2.09773, then the
height is 58/(p2.09773
2
) 4.1955. As a practical matter, it would probably be
best to round to one decimal place and construct a can of radius 2.1 and height
4.2 inches. ■
118 CHAPTER 2 Graphs and Technology
———
—
—
h
c
r
h
Figure 2–58
200
−50
15
Figure 2–59
EXERCISES 2.4
In Exercises 1–6, find the coordinates of the highest or lowest
point on the part of the graph of the equation in the given view-
ing window. Only the range of x-coordinates for the window are
given; you must choose an appropriate range of y-coordinates.
1. y 2x
3
3x
2
12x 1; highest point when
3 x 3
2. y 2x
6
3x
5
3x
3
2x
2
; lowest point when
3 x 3
3. y
x
4
2
7
x
1; lowest point when 10 x 10
4. y
x
2
2
1
x 2
; highest point when 5 x 5
5. y
(x
x
2
(
2
x
)
2
(x
1
)
3
4)
2
; highest point when 1 x 0
[Hint: Think small.]
6. y
(x
x
2
(
2
x
)(
x
1)
3
4)
2
; lowest point when 10 x 1
7. Find the highest point on the part of the graph of
y x
3
3x 2 that is shown in the given window. The an-
swers are not all the same.
(a) 2 x 0 (b) 2 x 2
(c) 2 x 3
8. Find the lowest point on the part of the graph of
y x
3
3x 2 that is shown in the given window.

(a) 0 x 2 (b) 2 x 2
(c) 3 x 2
9. The fuel economy y of a representative car (in miles per gal-
lon) can be approximated by
y .00000636x
4
.001032x
3
.067x
2
2.19x 8.6,
where x is the speed of the car (in miles per hour).* At what
speed does this car get the most miles per gallon?
†
10. Between 1997 and 2005, the number y of unemployed (in
thousands) was approximated by
y 53.4x
3
1772.33x
2
18,681.32x 69,188.1
(7 x 15),
where x 7 corresponds to 1997.
‡
In what year was unem-
ployment the highest?
11. In the situation described in Exercise 33 of Section 2.3
(page 113), how far from the building wall should the rope
meet the fence, if as little rope as possible is to be used.
12. In the situation described in Exercise 34 of Section 2.3
(page 113), how far should Anne run along the road if she
wants her trip to the helicopter to take the least possible
amount of time?
13. A farmer has 1800 feet of fencing. He plans to enclose a rec-
tangular region bordering a river (with no fencing needed
along the river side). What dimensions should he use to
have an enclosure of largest possible area?
14. A rectangular field will be fenced on all four sides. Fencing
for the north and south sides costs $5 per foot and fencing
for the other two sides costs $10 per foot. What is the max-
imum area that can be enclosed for $5000?
15. A rectangular area of 24,200 square feet is to be fenced on
all four sides. Fencing for the east and west sides costs $10
per foot and fencing for the other two sides costs $20 per
foot. What is the cost of the least expensive fence?
16. A fence is needed to enclose an area of 30,246 square feet.
One side of the area is bounded by an existing fence, so no
new fencing is needed there. Fencing for the side opposite
the existing fence costs $18 per foot. Fencing for the other
two sides costs $6 per foot. What is the cost of the least
expensive fence?
17. Find the dimensions of the rectangular box with a square
base and no top that has volume 20,000 cubic centime-
ters and the smallest possible surface area. [Hint: See
Example 3 in Section 2.3 (page 103).]
18. An open-top box with a square base is to be constructed
from 120 square centimeters of material. What dimensions
will produce a box
(a) of volume 100 cubic centimeters?
(b) with largest possible volume?
SECTION 2.4 Optimization Applications 119
19. A 20-inch square piece of metal is to be used to make an
open-top box by cutting equal-sized squares from each cor-
ner and folding up the sides (as in Example 3 on page 117).
The length, width, and height of the box are each to be less
than 14 inches. What size squares should be cut out to pro-
duce a box with
(a) volume 550 cubic inches?
(b) largest possible volume?
20. A cylindrical waste container with no top, a diameter of at
least 2 feet, and a volume of 25 cubic feet is to be con-
structed. What should its radius be if
(a) 65 square feet of material are to be used to construct it?
(b) the smallest possible amount of material is to be used to
construct it? In this case, how much material is needed?
21. If c(x) is the cost of producing x units, then c(x)/x is the
average cost per unit.* Suppose the cost of producing
x units is given by c(x) .13x
3
70x
2
10,000x and that
no more than 300 units can be produced per week.
(a) If the average cost is $1100 per unit, how many units
are being produced?
(b) What production level should be used in order to mini-
mize the average cost per unit? What is the minimum
average cost?
22. A manufacturer’s revenue (in cents) from selling x items per
week is given by 200x .02x
2
. It costs 60x 30,000 cents
to make x items.
(a) Approximately how many items should be made each
week to make a profit of $1100? (Don’t confuse cents
and dollars.)
(b) How many items should be made each week to have the
largest possible profit? What is that profit?
23. (a) A company makes novelty bookmarks that sell for
$142 per hundred. The cost (in dollars) of making
x hundred bookmarks is x
3
8x
2
20x 40. Because
of other projects, a maximum of 600 bookmarks per
day can be manufactured. Assuming that the company
can sell all the bookmarks it makes, how many should it
make each day to maximize profits?
(b) Owing to a change in other orders, as many as 1600 book-
marks can now be manufactured each day. How many
should be made to maximize profits?
24. If the cost of material to make the can in Example 4 on
pages 117–118 is 5 cents per square inch for the top and bot-
tom and 3 cents per square inch for the sides, what dimen-
sions should be used to minimize the cost of making the
can? [The answer is not the same as in Example 4.]
25. A certain type of fencing comes in rigid 10-foot-long seg-
ments. Four uncut segments are used to fence in a garden on
the side of a building, as shown in the figure on the next page.
*Based on data from the U.S. Department of Energy.
†
The most fuel efficient speed for a particular car may differ by 3 or
4 mph from the answer here.
‡
Based on data from the U.S. Department of Labor Statistics.
*Depending on the situation, a unit of production might consist of a
single item or several thousand items. Similarly, the cost of x units might
be measured in thousands of dollars.
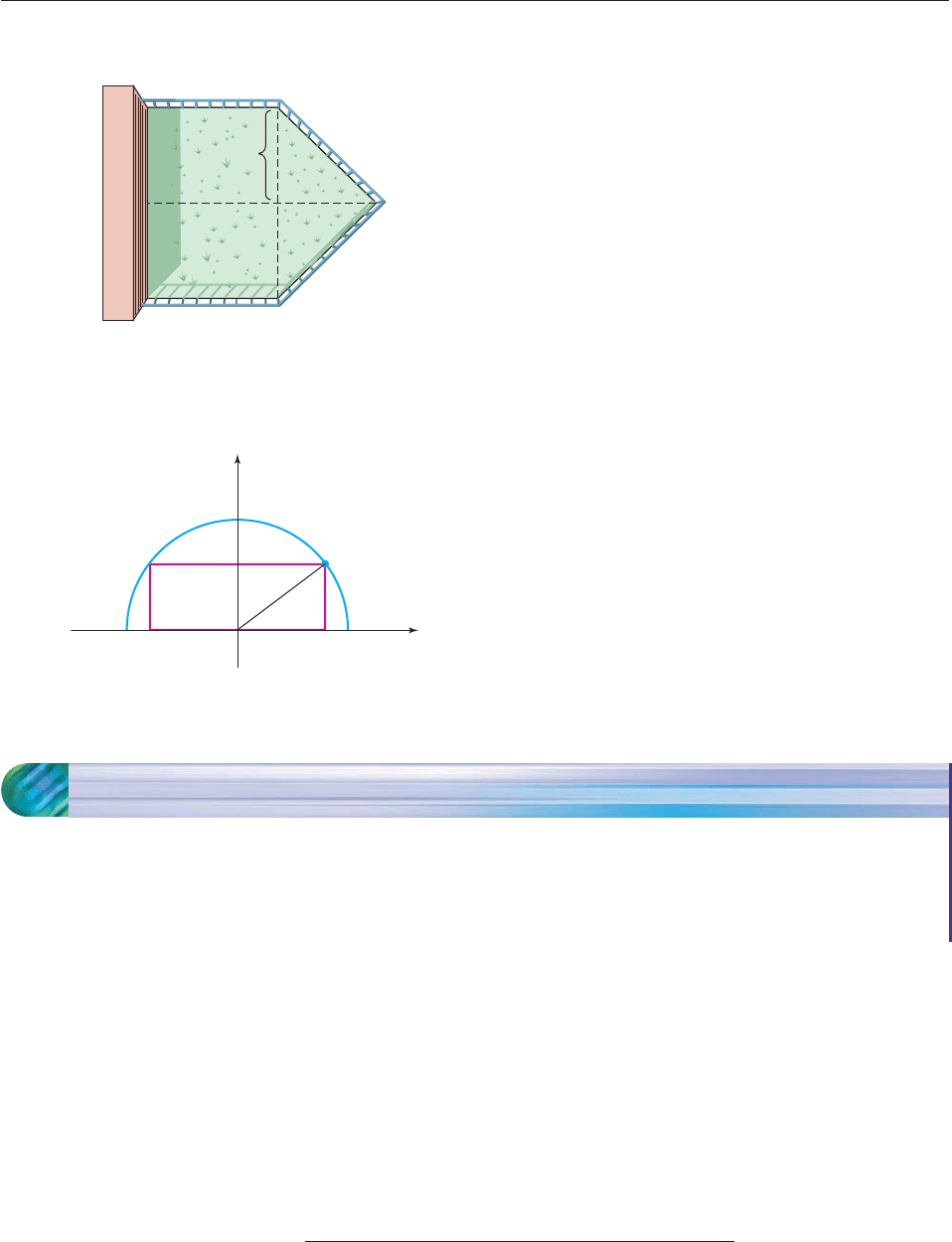
What value of x will result in a garden of the largest possi-
ble area, and what is that area?
26. A rectangle is to be inscribed in a semicircle of radius 2, as
shown in the figure. What is the largest possible area of
such a rectangle? [Hint: The width of the rectangle is the
second coordinate of the point P (why?), and P is on the top
half of the circle x
2
y
2
4.]
y
P
x
2
+ y
2
= 4
−22
2
0
x
−x
x
x
120 CHAPTER 2 Graphs and Technology
27. Find the point on the graph of y 5 x
2
that is closest to
the point (0, 1) and has positive coordinates. [Hint: The dis-
tance from the point (x, y) on the graph to (0, 1) is
(x 0
)
2
(
y 1)
2
; express y in terms of x.]
28. A manufacturer’s cost (in thousands of dollars) of produc-
ing x thousand units is x
3
6x
2
15x dollars, and the rev-
enue (in thousands) from x thousand units is 9x dollars.
What production level(s) will result in the largest possible
profit?
29. A hardware store sells ladders throughout the year. It costs
$20 every time an order for ladders is placed and $10 to
store a ladder until it is sold. When ladders are ordered x
times per year, then an average of 300/x ladders are in
storage at any given time. How often should the company
order ladders each year to minimize its total ordering
and storage costs? [Be careful: The answer must be an
integer.]
30. A mathematics book has 36 square inches of print per page.
Each page has a left side margin of 1.5 inches and top, bot-
tom, and right side margins of .5 inch. If a page cannot be
wider than 7.5 inches, what should its length and width be
to use the least amount of paper?
2.5 Linear Models*
■ Construct a linear model.
■ Gauge the accuracy of a linear model using residuals.
■ Use linear regression to find the least squares regression line.
■ Interpret the correlation coefficient r.
People working in business, medicine, agriculture, and other fields often need to
make judgments based on past data. For instance, a stock analyst might use the
past profits of a company to estimate next year’s profits, or a doctor might use
data on previous patients to determine the ideal dosage of a drug for a new
patient. In such situations, the available data can sometimes be used to construct
a mathematical model, such as an equation or graph, that approximates the
likely outcome in cases that are not included in the data. In this section, we
consider applications in which the data can be modeled by a linear equation.
The simplest way to construct a linear model is to use the line determined by
two of the data points, as illustrated in the following example.
Section Objectives
*This section is optional. It will be used only in clearly identifiable exercises or (sub)sections of the
text that can be omitted by those not interested.
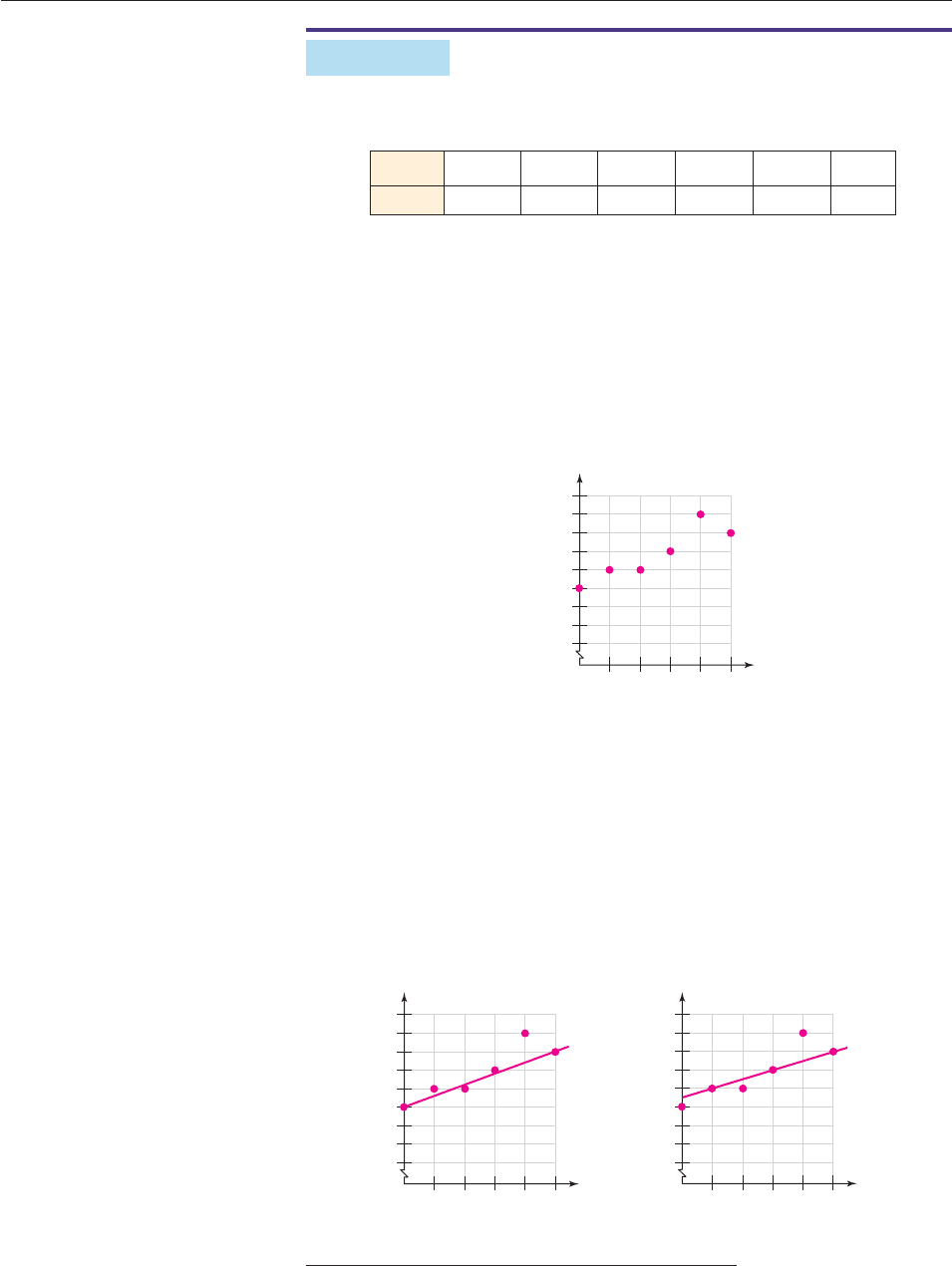
EXAMPLE 1
The profits of the General Electric Company (in billions of dollars) during the
first part of this decade are shown in the table.*
Let x 0 correspond to 2000, so that the data points are (0, 13), (1, 14), (2, 14),
(3, 15), (4, 17) and (5, 16).
(a) Make a scatter plot of the data points.
(b) Use the points (0, 13) and (5, 16) to find a line that models the data and graph
this line.
(c) Use the points (1, 14) and (5, 16) to find another line that models the data and
graph this line.
SOLUTION
(a)
Figure 2–60
Figure 2–60 shows that the data is approximately linear, so a line would be a
reasonable model.
(b) Points: (0, 13) and (5, 16)
Slope of line:
16
5
1
0
3
3
5
.6
Equation: y y
1
m(x x
1
)
y 13 .6(x 0)
y .6x 13
14
12345
12
10
18
16
x
y
SECTION 2.5 Linear Models 121
Year 2000 2001 2002 2003 2004 2005
Profit 13 14 14 15 17 16
*GE Annual Report 2005. The profit figures (net earnings) are rounded to the nearest billion.
(c) Points: (1, 14) and (5, 16)
Slope:
16
5
1
1
4
2
4
.5
Equation: y y
1
m(x x
1
)
y 14 .5(x 1)
y 14 .5x .5
y .5x 13.5
14
12345
12
10
18
16
x
y
Figure 2–61
14
12345
12
10
18
16
x
y
Figure 2–62
■
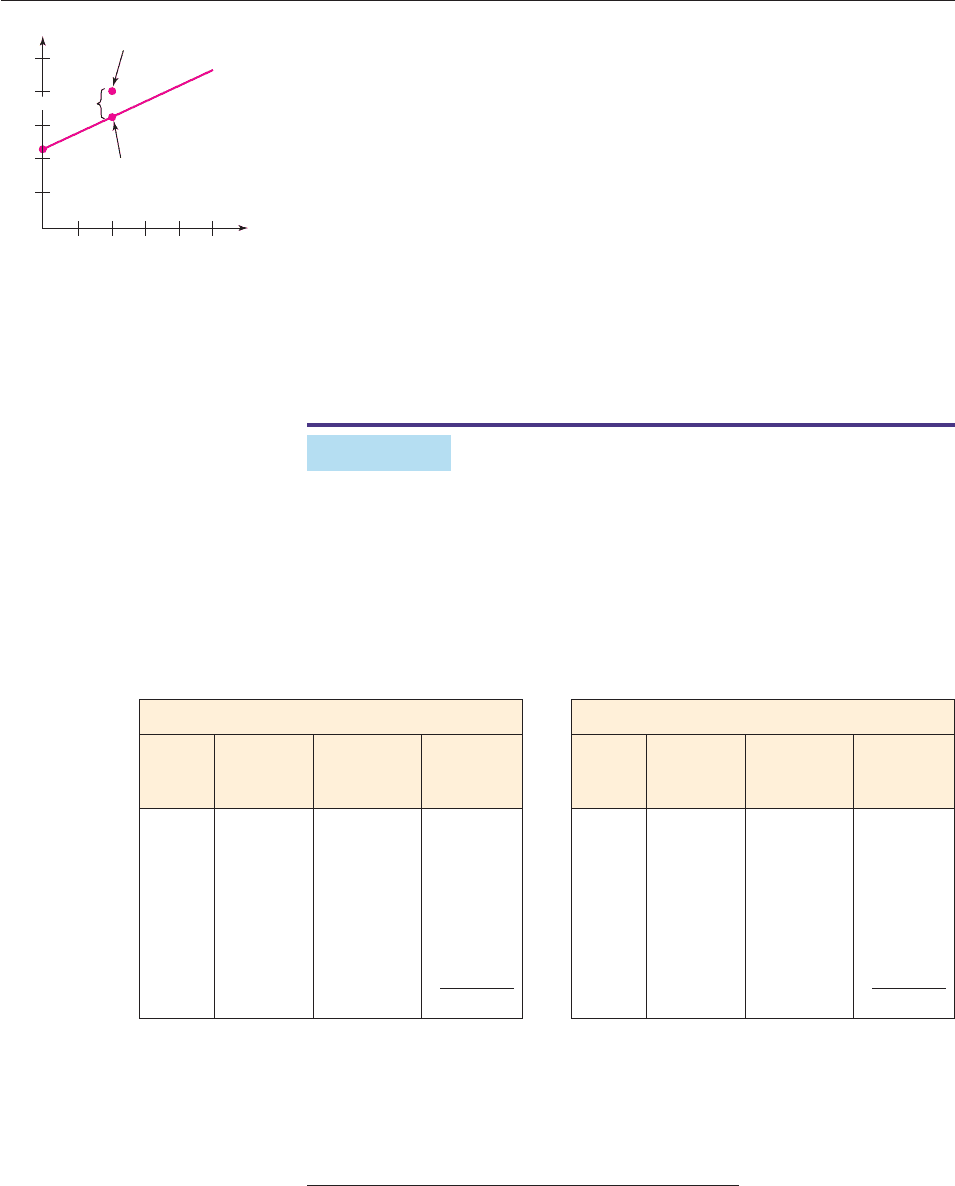
Both models in Example 1 seem reasonable. To determine the better one, we
first measure the errors in each model by computing the difference between the
actual profit p and the amount y given by the model. If the data point is (x, p) and
the corresponding point on the line is (x, y), then the difference p y measures the
error in the model for that particular value of x. The number p y is called a
residual. As shown in Figure 2–63, the residual p y is the vertical distance from
the data point to the line (positive when the data point is above the line, negative
when it is below the line, and 0 when it is on the line).
The universally accepted measure of the overall accuracy of a linear model is
the sum of the squares of its residuals—the smaller this number is, the better the
model fits the data points.* Using this number has the effect of emphasizing large
errors (those with absolute value greater than 1) because the square is greater than
the residual and minimizing small errors (those with absolute value less than 1)
because the square is less than the residual. So a smaller sum means that the line
has less overall error and fits the data better.
EXAMPLE 2
Two models for GE’s profits were constructed in Example 1:
y .6x 13 and y .5x 13.5.
For each model, determine the residuals, the squares of the residuals, and the sum
of these squares. Decide which model is a better fit.
SOLUTION The following tables give the required information.
122 CHAPTER 2 Graphs and Technology
(
x
, y) Model point
(
x
, p) Data point
Residual p − y
x
y
Figure 2–63
*The sum of the residuals themselves is less useful. As Exercise 1 shows, the residuals for two dif-
ferent models of the data may each sum to 0 (which doesn’t mean there is no error, but only that the
positive and negative errors cancel each other out). In contrast, the sum of the squares of the residuals
is 0 only when every residual is 0, that is, when all the data points lie on the model line.
y ⫽ .6x ⫹ 13
Data Model Squared
Point Point Residual Residual
(x, p)(x, y) p y (p y)
2
(0, 13) (0, 13) 0 0
(1, 14) (1, 13.6) .4 .16
(2, 14) (2, 14.2) .2 .04
(3, 15) (3, 14.8) .2 .04
(4, 17) (4, 15.4) 1.6 2.56
(5, 16) (5, 16) 0 0
Sum: 2.8
y ⫽ .5x ⫹ 13.5
Data Model Squared
Point Point Residual Residual
(x, p)(x, y) p y (p y)
2
(0, 13) (0, 13.5) .5 .25
(1, 14) (1, 14) 0 0
(2, 14) (2, 14.5) .5 .25
(3, 15) (3, 15) 0 0
(4, 17) (4, 15.5) 1.5 2.25
(5, 16) (5, 16) 0 0
Sum: 2.75
Since the sum of the squares of the residuals of y .5x 13.5 is less than the sum
of the squares of the residuals of y .6x 13, we conclude that y .5x 13.5
fits the data better. ■

LINEAR REGRESSION
The following fact, which requires multivariate calculus for its proof, shows that
there is always a best possible model for linear data.
The computational process for finding the least squares regression line is
called linear regression. The linear regression formulas are quite complicated
and can be tiresome to use with a large data set. Fortunately, however, linear
regression routines are built into most calculators and are also available in spread-
sheet and other computer programs.
EXAMPLE 3
As we saw in Example 1, GE’s profits (in billions of dollars) during the first part
of this decade were as follows.
Use technology to find the least squares regression line that models this data.
Graph the data points and the regression line.
SOLUTION Let x 0 correspond to 2000, so that the data points are (0, 13),
(1, 14), and so on. Enter the data points as two lists in the calculator’s statistics
editor (Figure 2–64) and make a scatter plot of the data (Figure 2–65).*
SECTION 2.5 Linear Models 123
Linear Regression
Theorem
For any set of data points, there is one and only one line for which the sum
of the squares of the residuals is as small as possible. This line is called the
least squares regression line.
Year 2000 2001 2002 2003 2004 2005
Profit 13 14 14 15 17 16
*Directions for doing this are in the Technology Tip on page 88.
†
See the Technology Tip at the end of this section for directions on how to do this.
Figure 2–64
20
1
0
6
Figure 2–65
In the statistics calculation menu, choose linear regression (Figure 2–66 on the
next page) and enter the list names and the variable where the regression line
graph should be stored (Figure 2–67).
†
Press ENTER to obtain the equation of the
regression line (Figure 2–68).
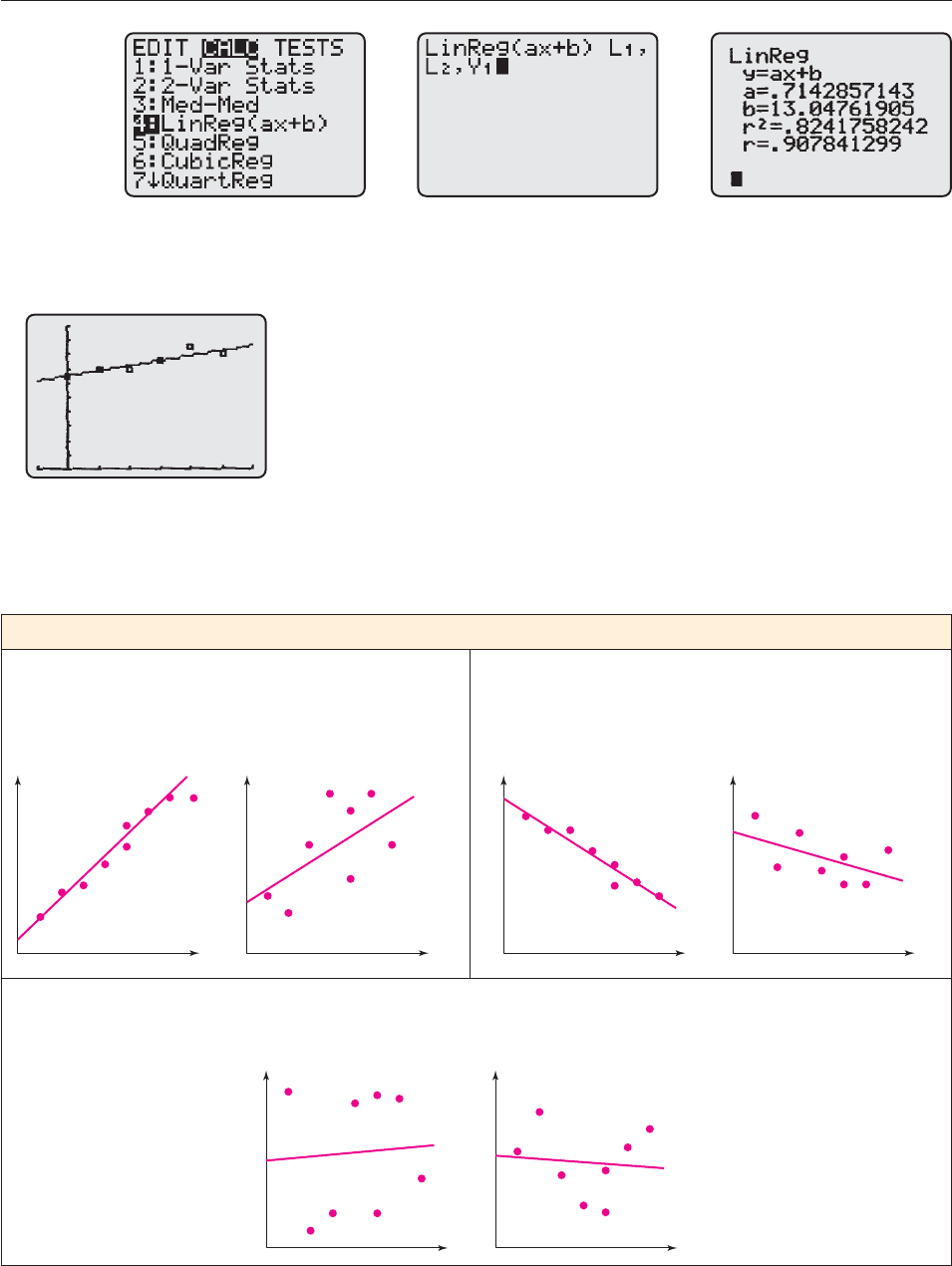
Figure 2–66 Figure 2–67 Figure 2–68
So the equation of the least squares regression line, which best fits the data, is
y .7142857143x 13.04761905.
Finally, press GRAPH to see the graph of the regression line (Figure 2–69). ■
In addition to the coefficients of the regression line, Figure 2–68 contains a
number r (and its square). The number r, which is called the correlation coeffi-
cient, is always between 1 and 1. It is a statistical measure of how well the
regression line fits the data. The closer the absolute value of r is to 1, the better the
fit. For instance, the regression line in Example 3 is a good fit because r .91, as
shown in Figure 2–68. When r 1 or r 1, the fit is perfect: All the data points
are on the regression line. Conversely, a regression coefficient near 0 indicates a
poor fit, as shown in the summary below.
124 CHAPTER 2 Graphs and Technology
Figure 2–69
20
1
0
7
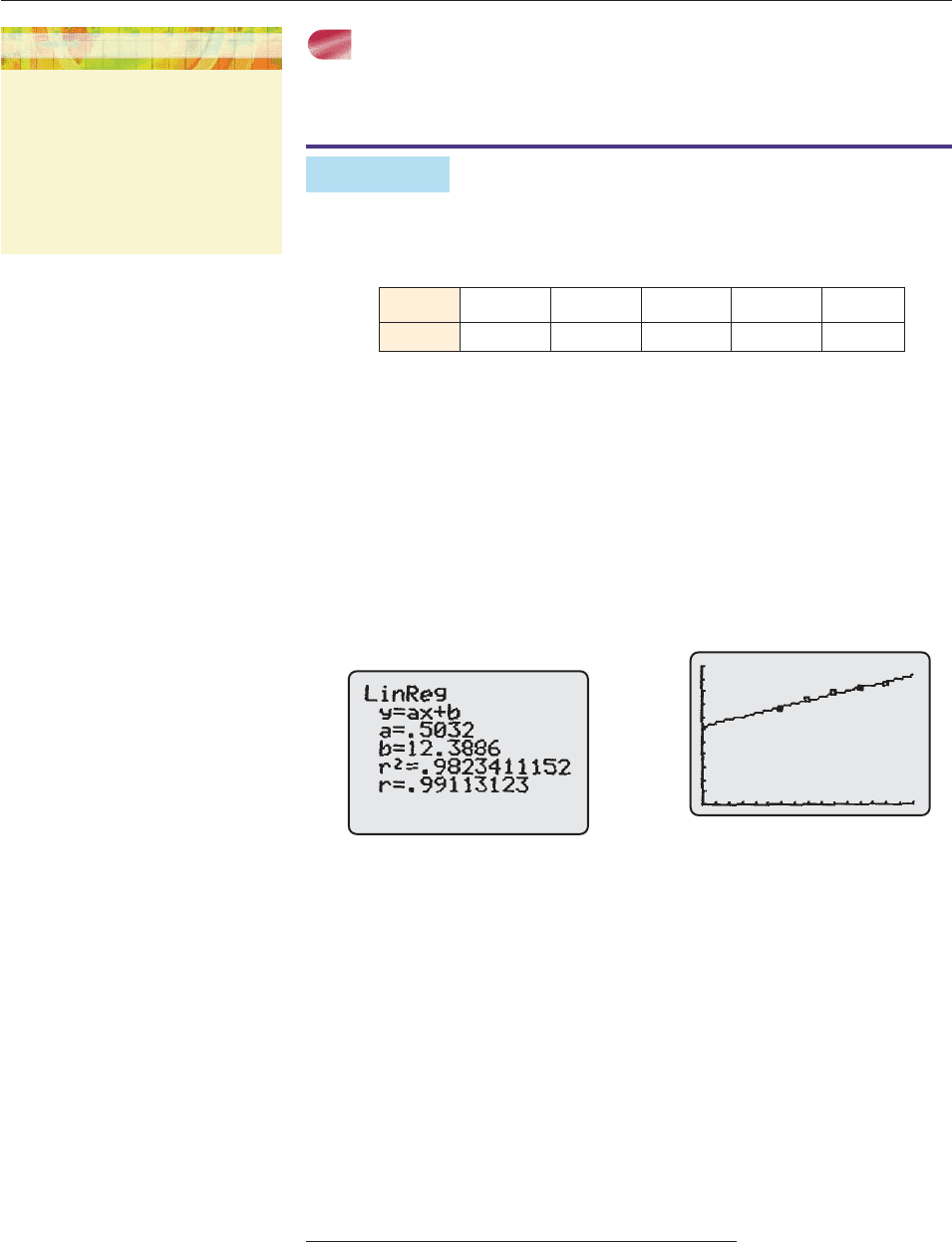
Correlation Coefficient r
0 b r X 1 1 X r b 0
The regression line has positive slope and moves upward The regression line has negative slope and moves downward
from left to right. As x increases, y also increases. We say from left to right. As x increases, y decreases. We say that the
that the data has positive correlation. Examples: data has negative correlation. Examples:
r is very close to 0 (regardless of sign)
The regression line is a very poor fit for the data. We say that the data has no correlation. Examples:
x
y
x
y
x
y
x
y
x
y
x
y
APPLICATIONS
The various possibilities in the preceding box are illustrated in the following
applied examples.
EXAMPLE 4
The table shows the poverty level for a family of four in selected years (families
whose income is below this level are considered to be living in poverty).*
SECTION 2.5 Linear Models 125
*U.S. Census Bureau.
Year 1996 1998 2000 2002 2004
Income $15,141 $16,660 $17,603 $18,392 $19,307
TECHNOLOGY TIP
The correlation coefficient r is labeled
“corr” on TI-86/89, and also on HP-39gs
(where it is in the NUM/STATS menu).
If r fails to appear on TI-84, go
to CATALOG, select “Diagnostics On,”
and press ENTER twice. Then re-run
the regression calculation.
(a) Use linear regression to find an equation that models this data.
(b) If the model fits the data well, use the equation to estimate the poverty level
in 2003 and in 2008.
SOLUTION
(a) Let x 0 correspond to 1990 and write the income in thousands (for instance,
15.141 in place of 15,141). Then the data points are (6, 15.141), ...,
(14, 19.307). We proceed as in Example 3 to find the least squares regression
line (Figure 2–70) and its graph (Figure 2–71).
Figure 2–70
Figure 2–71
22
0
0
16
The correlation coefficient r .99 shows that the data is positively correlated
and that the model is an excellent fit. The graph confirms this.
(b) The year 2003 corresponds to x 13. To estimate the poverty level in 2003,
substitute x 13 in the regression equation:
y .5032x 12.3886
.5032(13) 12.3886
18.9302.
So the regression model estimates the poverty level in 2003 to be $18,930.
The actual level in that year was $18,811, a difference of only $119. Simi-
larly, for 2008 (x 18) the model estimates the poverty level to be
y .5032(18) 12.3886 21.4462
