Hua C., Wong R. Differential Equations and Asymptotic Theory in Mathematical Physics
Подождите немного. Документ загружается.


312
In order to get the exact boundary controllability in the quasilinear
hyperbolic case, we present a constructive method which works for general
quasilinear hyperbolic systems with general nonlinear boundary conditions
at least in one-dimensional case. The main idea can be shown
as
follows.
In order to realize the exact boundary controllability, it is only necessary
to find a time
T
>
0
such that the given hyperbolic equation (system)
admits
a
classical solution
u
=
u(t,z)
on the domain
[0,
T]
x
n,
which
verifies simultaneously the initial condition
t=O:
u='p(z),
zER
(2)
and the final condition
(1).
In fact, putting
u
=
u(t,
x)
into the boundary
conditions, we get immediately the boundary controls. By uniqueness,
the classical solution to the corresponding mixed initial-boundary value
problem with the initial data
'p
must be
u
=
u(t,x),
which automatically
satisfies the given final data
$.
Moreover, if the solution
u
=
u(t,
z)
constructed above also satisfies
a
part
of
boundary conditions, then we need only to put
u
=
u(t,z)
into
the other part of boundary conditions to get the corresponding boundary
controls, and, as a result, the number
of
boundary controls will be reduced
and the boundary controls can be asked to act only on a part of boundaries,
however, the controllability time will be enlarged.
Of course, for the purpose of application, the controllability time
T
will
be asked to be
as
small
as
possible.
3.
Statement on the exact boundary controllability
of
unsteady flows in a network
of
open canals
We now consider unsteady flows in a network composed
of
N
horizontal and
cylindrical canals. Let
La
be the length of the a-th canal,
a1
and
a0
the
z-coordinates
of
two ends of the a-th canal:
La
=
a1
-
ao
(a
=
1,
. .
.
,
N).
Suppose that there is no friction, the corresponding Saint-Venant system
(cf.
[2],
[14])
is
=
0,
tLO,
ao<~<al
(a=l,...,N),
(3)
where
for
the a-th canal,
A(a)
=
A(")(t,z)
stands
for
the area of the cross
section at
z
occupied by the water at time
t,
V(")
=
V(")(t,z)
the average

313
velocity over the cross section and
where
g
is
the gravity constant, constant
Yd")
denotes the altitude of the
bed
of
the a-th canal and
ha
=
h,(A("))
(5)
is the depth of the water in the a-th canal,
ha
(A("1)
being a suitably smooth
function
of
A(")
such that
hL(A("))
>
0.
(6)
The initial condition is
t=O:
(A("),V("))=(A~)(X),VJ")(X)>,
UO<X_<U~
(~=1,.-.
,N).
When
x
=
a0
(resp.
x
=
al)
is
a
simple nodelthe boundary condition on
x
=
a0
(resp.
x
=
u1)
is
given by
(7)
x
=
a0
(resp.
x
=
al)
:
A(")V(a)
=
qt)(t)
(resp.
qp)(t)).
(8)
When
,
for
instance,
x
=
a0
is
a
multiple node and the open canals jointed
at
x
=
a0
are indexed by
5,
6,
3,
. .
,
the interface conditions
at
x
=
a0
are given by the total flux-type interface condition
__.
x
=
a0
:
C
&A(i)V(i)
=
Qa,(t)
(9)
i=jj
b
E
...
0,
and the energy-type interface conditions
(cf.
121,
1141).
Consider an equilibrium state
(A("),
V("))
=
(A?), Vd"')
with
A?)
>
0
(a
=
1,.
.
.
,
N)
for system
(3),
which belongs to
a
subcritical case, i.e.,
IVd"'l
<
dgA?)h;(A?))
(a
=
1,
.. .
,
N),
(11)
and satisfies the energy-type interface conditions
(10).

314
In a neighbourhood of any given subcritical equilibrium state
(A("),
V(a))
=
(A?),
VJ"')
(a
=
1,.
. .
N),
(3)
is
a
hyperbolic system with
real eigenvalues
For
a
=
l,...
,N,
introducing the Riemann invariants
r,
and
s,
as
follows:
(13)
2r,,=
v(")
-
vJa)
-
G, (A(")),
2s,
=
v(a)
-
+
G,(A(~)),
where
we have
V(")
=
r,
+
s,
+
Vi"',
A(")
=
H,(s,
-
r,)
>
0,
where
H,
is the inverse function of
G,(A(,)),
H,(O)
=
A:?)
and
(17)
Taking
(r,,
s,)
(a
=
1,.
. .
,
N)
as
new unknown variables, the equi-
librium state
(A("),
V("))
=
(At),
V;"))(a
=
1,.
.
,
N)
corresponds to
(r,,~,)
=
(0,O)
(a
=
l,...
,N)
and system
(3)
can be reduced
to
the
following system of diagonal form:
(a=
l,...
,N),
(19)
315
The boundary condition (8) on
z
=
a0
is now written
as
(21)
z
=
a0
:
(r,
+
s,
+
VJ"')H,(S,
-
r,)
=
qo
(a)
(t).
It
is easy to see that in
a
neighbourhood of
(r,,s,)
=
(O,O),
(21)
can be
equivalently rewritten as
z
=
a0
:
s,
=
ga(t,
r,)
+
h,(t)
r,
=
~,(t,
s.1
+
L,(t),
(22)
(23)
(24)
or
z
=
a0
:
in which
ga(t,O)
3
ij"(t,O)
=
0
and
C1
norm of
ha(.)
(resp.
La(.))
small enough
(25)
C1
norm of
(q(,)(-)
-
At)VJ"))
small enough.
The interface conditions
(9)-(10)
on
z
=
a0
are now written as
2
=
ao
:
C
f(ri
+
si
+
V:))Hi(si
-
ri)
=
Qa,(t)
(26)
i=ij
b
E
...
I0
and
1
2
2
5
=
a0
:
-
(ra
+
sa
+
VJZ))
+
ghi(Hi(si
-
ri))
+
gYb(i)
1
=
(#-"
+
s,
+
Vd"))2
+
gh,(H,(s,
-
r,))
+
,yp)
(27)
-
(i
=
b,
c,
.
*
.).
For the purpose of the exact boundary controllability of unsteady flows
in a network of open canals, we want to find
a
time
T
>
0
such that for
any given initial data
t
=
0
:
(A("), I""')
=
(A?)(z),
L$"'(x)),
a0
_<
IC
_<
a1
(a
=
1,
...
,N)
(28)
and any given final data
t
=
T
:
(A("), V'"))
=
(A$)(z),
V$'(z)),
a0
5
z
5
a1
(a
=
1,.--
,N)
in
a
C1
neighbourhood of the subcritical equilibrium state
(At), VJ"))
(a
=
1,.
. .
,
N),
there exist suitable boundary flux controls at some sim-
ple nodes and multiple nodes, such that the corresponding mixed initial-
boundary value problem for Saint-Venant systems
(3)
with the initial data
(29)

316
and the corresponding boundary conditions and interface conditions admits
a
unique semi-global piecewise
C1
solution on the time interval
0
<
t
5
T,
which verifies exactly the final data.
To
this end, it suffices to construct
a
piecewise
C1
solution to Saint-
Venant system
(3)
on
the time interval
0
<
t
<
T,
which satisfies the
initial condition on
t
=
0,
the final condition on
t
=
T,
all the energy-type
interface conditions and a part of flux boundary conditions and total flux-
type interface conditions.
If
we can
do
so,
putting this solution to the rest
of flux boundary conditions and total flux-type interface conditions, we get
the desired flux boundary controls and total flux interface controls which
realize the exact boundary controllability.
In what follows we will see that there are still many possibilities to get
this kind of semi-global piecewise
C1
solution. The main principle is to
make the number of controls
or
the optimal controllability time as small
as
possible. However,
for
a smaller number of controls, we need a larger
optimal controllability time, and vise versa.
4.
Preliminaries for quasilinear hyperbolic systems of
diagonal form
Since Saint-Venant system can be reduced to
a
quasilinear hyperbolic sys-
tem of diagonal form, in this section we first give some results for quasilinear
hyperbolic systems of diagonal form
duz
dUa
-
+
&(u)-
=
Fz(u)
at
ax
(i
=
1,.
.
.
,
n),
where
u
=
(~1,.
. .
,u,)~
is the unknown vector function of
(t,x),
Xi(.)
and
Fi(u)
are
C1
functions of
u
and
Fi(0)
=
0
(i
=
1,.
.
*
3.1.
(31)
Suppose that on the domain under consideration
&(u)
<
0
<
X,(u)
(r
=
1,e.a
,m;
s
=
m+l,...
,n).
(32)
Consider the mixed initial-boundary value problem for system
(30)
with
the following initial condition
t=O:
u=cp(z)
O<X<L
(33)
and boundary conditions
x=O:
U,
=G,(t,ul,... ,um)+Hs(t)
(s=m+l,...
,n),
(34)

317
z=L:
U,=G~(~,U~+~,...
,un)+HT(t)
(~=1,...
,m),
(35)
where
(p,
Gi
and
Hi(i
=
1,.
.
+
,
n)
are
C1
functions with respect to their
arguments, and, without loss of generality, we assume that
Gi(t,O,*..
,0)
EO
(i
=
l,...
In).
(36)
Moreover, the conditions of
C1
compatibility are assumed to be satisfied
at
points
(t,
Z)
=
(0,O)
and (0,L) respectively.
Lemma
4.1
([15]):
Under the assumptions mentioned above, for any
preassigned and possibly quite large
T
>
0,
the mixed initial-boundary
value problem
(30)
and
(33)-(35)
admits a unique
C1
solution (called the
semi-global
C1
solution)
u
=
u(t,
Z)
with small
C1
norm on the domain
R(T)
=
{(t,~)l
0
5
t
5
T,
0
5
z
5
L},
(37)
provided that the
C1
norms
II(pllClpL1
and
IIHillclpT]
(i
=
1,e.a
,n)
are
small enough (depending on
T).
We have the following two theorems which lead to the local exact bound-
ary controllability directly (cf.
[16]-[18]).
Theorem
4.1:
Let
Under the assumptions mentioned at the beginning of this section, for any
given initial state
V(Z)
and final state
G(z)
with small
C1
norms
II(pllcl[o,L]
and
Il$llcl[o,L],
there exists a
C1
solution
u
=
u(t,~)
with small
C1
norm
on the domain
R(T)
=
{(t,Z)l
0
5
t
5
T,
0
5
Z
5
L},
(39)
which satisfies simultaneously the initial condition
(33)
and the final con-
dition
t=T:
U=+(Z),
O~Z~L.
(40)
To
construct this kind of solution is a non-standard problem. Roughly
speaking, the procedure contains the following steps:
1)
By means of the initial data we solve a forward mixed problem to
get
a
semi-global
C1
solution on the time interval
0
5
t
5
TI,
where
2)
By means of the final data we solve
a
backward mixed problem to
;
>TI
x
$.
get a semi-global
C1
solution on the time interval
T
-
TI
.<
t
.<
T.

318
L
3)
By suitably supplying the value of
u
for
Tl
5
T
5
T
-
TI
on
x
=
2
and changing the order of
t
and
x,
we solve the rightward and leftward
mixed problem respectively to get the desired solution.
From Theorem
4.1,
there exist boundary controls
Hi
E
C1[O,T]
(i
=
1,
.
.
,
n)
with small
C1
norm, which realize the exact boundary controlla-
bility. Here, the number of boundary controls is equal to
n,
the number of
unknown variables, and the boundary controls act on two ends.
This procedure is denoted by
Figure
1.
Here,
”x”
stands for the starting point, the middle point
x
=
$,
on
which the value of solution is given,
”0”
the arriving end on which the
value
of
solution can be determined and then there are boundary controls,
and
”
-”
dedicates the direction pointing to the control end, along which
we solved our rightward or leftward problem respectively.
Theorem
4.2:
Let
Under the assumptions mentioned at the beginning of this section, suppose
furthermore that
n=2m (42)
and in a neighbourhood of
u
=
0
the boundary condition
(34)
can be
equivalently rewritten as
5
=
0:
u,
=
G,(t,um+l,...
,un)
+R,.(tj
(r
=
I,...
,m),
(43)
where
c,
and
R,(r
=
1,.
.
.
,m)
are
C1
functions with respect to their
arguments,
G,(t,O,...
,O)
=
0
(r
=
I,...
,m)
(44)
and, consequently,
(45)
c1
norms
of
H,(.)
(s
=
m
+
1,
. .
.
,
n)
small enough
H
c1
norms
of
R,(.)
(r
=
1,.
. .
,
m)
small enough.

319
Then, for any given initial state
‘p,
final state
$J
and boundary func-
tions
H,(t)
(s
=
rn
+
I,...
,n)
at x
=
0
with small
C1
norms
conditions of
C1
compatibility are satisfied at points (t,x)
=
(0,O)
and
(T,O)
respectively, there exists a
C1
solution
u
=
u(t,x) with small
C1
norm on the domain
R(T),
which satisfies the initial condition
(33),
the
final condition
(40)
and the boundary condition
(34)
on x
=
0.
The procedure
of
constructing this solution contains the following steps:
1)
By means of the initial data and the boundary conditions
(34)
on
x
=
0,
we solve a forward mixed problem to get a semi-global
C1
solution
on the time interval
0
5
t
5
TI,
where;
>
TI
M
;.
2)
By means
of
the final data and the boundary conditions
(43)
on
2
=
0,
we solve a backward mixed problem to get a semi-global
C1
solution
on the time interval
T
-
TI
5
t
5
T.
3)
Suitably supplying the value of
u
for
TI
5
T
5
T
-
TI
on x
=
0,
such that the boundary conditions
(34)
on
x
=
0
are satisfied for the whole
interval
0
5
t
5
T,
and changing the order
oft
and x,we solve the rightward
mixed problem to get the desired solution.
From Theorem
4.2,
there exist boundary controls
HT(t)
(r
=
1,.
.
. ,
m)
at x
=
1
with small
C1
norms
IIHT]IclpTl
(r
=
l,...
,rn),
which realize
the exact boundary controllability. Here, the number of boundary controls
is equal to
m
=
2
and the boundary controls act only on one end, however,
the controllability time is doubled.
ll’pllCl[O,L],
lllClllCl[O,L]
and
II~SllCl[O,T]
(s
=
m
+
I,...
,n)>
such that the
This procedure is denoted by
A
Figure
2.
Here
”0”
stands
for
the starting end on which there are no boundary
controls,
”0”
the arriving end on which there are boundary controls, and
”
-”dedicates the direction of solving the rightward problem and points
to the control end.
5.
Corresponding consideration for Saint-Venant system
5.1.
For
a
single canal with flux boundary conditions on both ends, Theo-
rems
4.1
and
4.2
can be applied directly to get the results denoted by (cf.
1141)
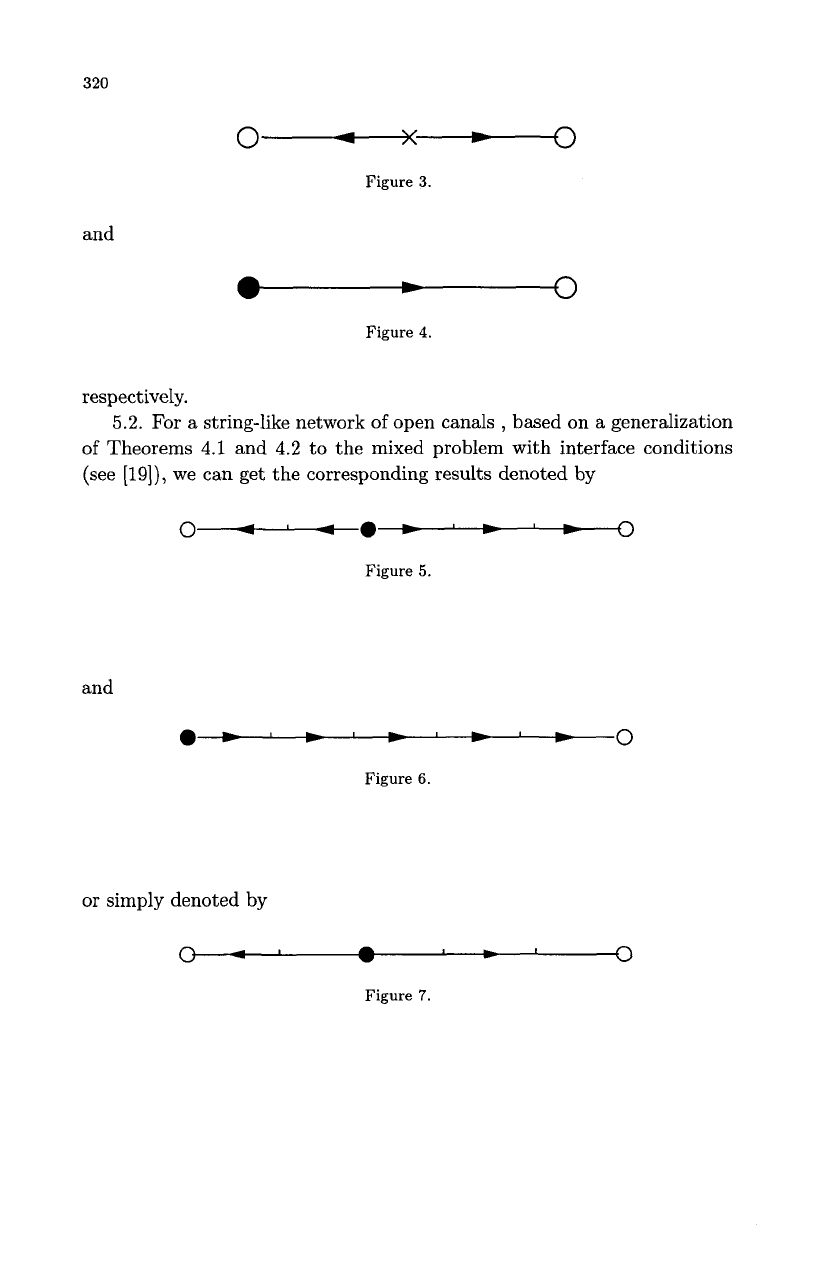
320
0-V
Figure
3.
and
A
Figure
4.
respectively.
5.2.
For
a
string-like network of open canals
,
based on a generalization
of Theorems
4.1
and
4.2
to the mixed problem with interface conditions
(see
[19]),
we can get the corresponding results denoted by
0-0-
I
=
L
-
0
Figure
5.
and
o-'='=m
=-I
=
0
Figure
6.
or simply denoted by
L
-
0
Figure
7.

321
and
0
I-
-
0
Figure
8.
Here, the piecewise
C1
solution is still constructed along the direction
-+
from the node
"0"
to the end
"0".
In the first case, the node
is
anyone
of
double nodes and both two simple nodes are the control ends
"0".
There
are two
flux
controls acting on both simple nodes respectively; while, in the
second case, the end
"0"
is a simple node and another simple node is the
control end
"0".
There is only one flux control acting on a simple node.
Both cases are completely similar to the cases
for
a single canal, however,
the controllability time should be much larger: it
is
a
corresponding sum
of
controllability time for each individual canal (for the detail, see
[19])
.
5.3.
By rescaling and folding all corresponding 2-intervals to an interval
0
5
2
5
1,
Theorem
4.2
can be almost directly applied to a star-like
network
of
open canals. Then we can get the desired piecewise
C1
solution
by solving the problem
from
the joint end (multiple node) to all simple
nodes, as denoted by
P
Figure
9.
Here, all simple nodes are the control ends "o", while there is no control
on the joint end
"e".
The number of boundary flux controls is equal to the
