Houze Robert A., Jr. Cloud Dynamics

Подождите немного. Документ загружается.

11.2 Circulation at a Front 449

thickness contours. The

coLdfront marks the warm edge of the frontal zone in the

cold polar air moving equatorward and eastward on the west side of the cyclone.

The

warm front marks the warm edge of the receding frontal zone on the east side

of the cyclone; it indicates the advancing edge of the tropical air flowing poleward

at the 1000-mb level. Since the cold front advances more rapidly than the warm

front recedes (cf. Fig. 11.4a and b), the warm sector progressively narrows, and

warm-sector air is lifted off the surface by the time of Fig. 11.4c. At this stage, the

developing cyclone is said to be

occluded. At 1000mb an occludedfront is drawn

along the line of maximum temperature extending from the point where the cold

and warm fronts meet to the center of the low-pressure system.

Figure 11.4 suggests that the low-level cyclone and fronts appear and develop

simultaneously as a continuous process in the context of a baroclinic wave devel-

opment. In many real cases, a baroclinic wave that is well defined at upper or

middle levels, but weak in the lower atmosphere, moves over a

pre-existing low-

level frontal zone. This process is indicated schematically in Fig. 11.5. When the

area of upward motion ahead of the trough

ofthe

upper-level wave (Figs. 11.2 and

11.3) appears over the pre-existing front, cyclogenesis and frontogenesis at low

levels are hastened. The surface cyclone is excited at a location along the pre-

existing front, as shown in Fig. 11.5. The surface front intensifies and becomes

distorted with cold and warm fronts extending out of the low center and moving

and developing in a manner not unlike that shown in Fig. 11.4.

11.2 Circulation at a Front

While the general vertical motion pattern in a developing baroclinic wave (Fig.

11.3)goes a long way toward explaining the cloud patterns associated with extra-

tropical cyclones, it does not adequately account for the details of the circulations

producing the clouds. The patterns of temperature and geostrophic wind in a

baroclinic wave are frontogenetical, which means that the large-scale winds tend

to concentrate the temperature gradients and form fronts. The vertical circulation

required to maintain thermal-wind balance-" is thus locally concentrated and

intensified in the vicinity of frontal zones. In this section, we investigate the

dynamics of frontogenesis to gain a better appreciation of the cloud-forming circu-

lations in extratropical cyclones. To establish some basic features of frontogene-

sis, we will first review the dynamics of dry frontogenesis (Sees. 11.2.1 and

11.2.2). Then we will examine moist frontogenesis, the case most relevant to

cloud dynamics, as an extension of the dry theory (Sec. 11.2.3). Finally, we will

inspect some example calculations of the vertical circulation at a front (Sec.

11.2.4).

l89 Actually, the circulation at strong fronts is probably not exactly in thermal-wind balance, and

this imbalance may be important in the frontal circulation. However, the balanced flow at a front is a

good first approximation and is sufficient for our purposes in this chapter.

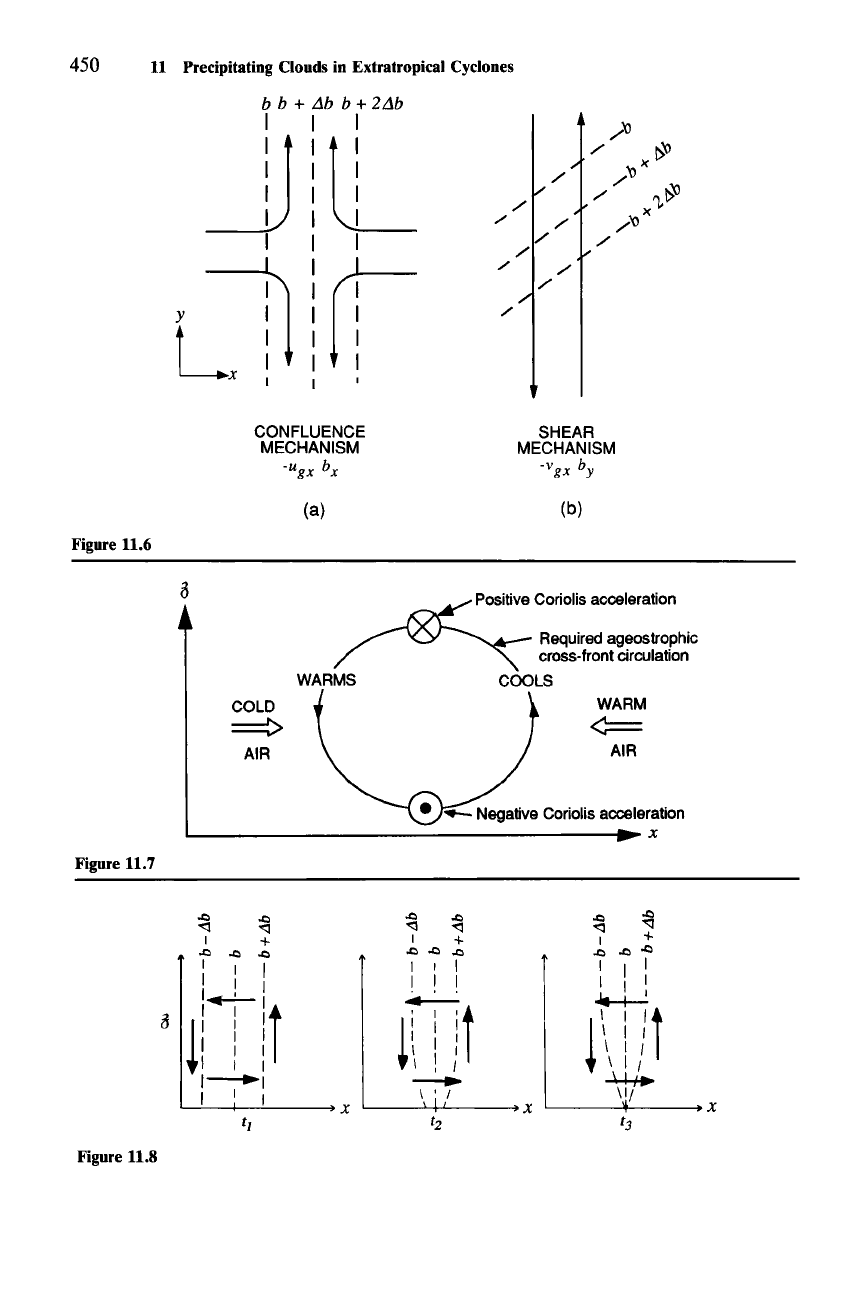
450 11 Precipitating Clouds in Extratropical Cyclones

Figure 11.6

b b + t1b b + 2t1b

I I

JJlL

I I

CONFLUENCE

MECHANISM

-u

(a)

SHEAR

MECHANISM

-v

(b)

Figure 11.7

COLD

AIR

Coriolis acceleration

Required ageostrophic

cross-front circulation

WARMS COOLS

WARM

AIR

Figure 11.8

I +

,Q ,Q

I I I

~jiii

I I

'---'1

I I I

,Q ,Q

"::] "::]

I +

,Q,Q,Q

I I I

! !

....--

i i

\ I I

\ , /

--.

\ ' I

,Q ,Q

: I :

\ t I I

\ I I

-W..+.

, 1/

11.2 Circulation at a Front

451

11.2.1 Quasi-Geostrophic Frontogenesis

To keep the discussion as simple as possible, we will consider fronts from a two-

dimensional perspective, examining the circulation in a vertical plane oriented

perpendicular to a front oriented parallel to the y-axis.

290 In the case of the quasi-

geostrophic motions considered in Sec. 11.1, this circulation is expressed by the

x-component of (11.13):

- 2 - 2

N W

f U

= 2Q

(11.16)

The Q-vector component

is thus the forcing for the ageostrophic circulation

w) at the front, in the absence of friction and diabatic heating. From the

y-cornponent of (11.10):

(11.17)

can be seen that Q, contributes, along with the horizontal gradient of

to the

rate at which the x-gradient of

b is becoming concentrated within a fluid parcel. If

the horizontal gradient

b is increasing, the parcel is said to be undergoing

frontogenesis. If the gradient is decreasing, the situation is referred to asfrontoly-

sis.

The two terms contributing to QI , as defined in (11.11), are -uRxb

which is

called the

confluence

mechanism,

and -vRxb

which is referred to as the shear

mechanism.

These mechanisms are illustrated in Fig. 11.6. An important differ-

ence in the two mechanisms is that the confluence mechanism can be active when

there is no gradient of

b in the y-direction, and the shear mechanism can be active

when there is no gradient of

b in the x-direction. Some theoretical analyses of

frontogenesis are based entirely on either one or the other mechanism. In reality,

both mechanisms are active, and the winds and isotherms in the vicinity of a front

in a developing cyclone (e.g., the low-level geostrophic wind and thickness lines

in Fig. 11.4) are composed of a combination of the two mechanisms.

290 The discussion in this subsection is extracted mainly from the excellent review of Hoskins

(1982). Further very useful reviews are given by Bluestein (1986) and Keyser (1986).

Figure 11.6 Confluence and shear mechanisms of frontogenesis. Streamlines of the horizontal

geostrophic wind (v

= ugi +

vgj)

are superimposed on the field of b. (Adapted from Hoskins, 1982.)

Figure 11.7 Quasi-geostrophic frontogenesis forced by the deformation mechanism. Double

arrows show geostrophic flow in x-direction. The geostrophic flow is in thermal wind balance.

Temperature field is indicated by locations of warm and cold air. Flow is into the page at upper levels

«(8))

and out of the page at lower levels (circled dot). The ageostrophic flow required to maintain

thermal wind balance is indicated by the streamline. The upper-level component

ofthe

flow normal to

the page is being accelerated by the action of the Coriolis force on the ageostrophic circulation, while

the lower-level component is negatively accelerated. (Adapted from Hoskins,

1982. Reprinted with

permission from Annual Reviews, Inc.)

Figure 11.8 Idealization of the evolution of the

b field at a sequence of times

(II,

12, and 1

in the

case of quasi-geostrophic frontogenesis. Arrows show the ageostrophic cross-front circulation.

(Adapted from Bluestein,

1986. Reproduced with permission from the American Meteorological

Society.)

452 11 Precipitating Clouds in Extratropical Cyclones

The relations (11.16) and (11.17) are useful in formulating the theory of quasi-

geostrophic frontogenesis,

which is an oversimplification of real atmospheric

frontogenesis but nonetheless a valuable foundation on which to build more realis-

tic theories, to be considered below. Henceforth, it will be assumed that the

geostrophic wind components

and v

are invariant in the front-parallel y-direc-

tion and that the front-parallel flow has no ageostrophic component. Since geo-

strophic motion is horizontally nondivergent [as is evident from (2.68)], the conti-

nuity equation (11.8) becomes

+ w

Mass continuity is then satisfied by a stream function

1Jr

of the form

(ua,w)

(-~,~)

(11.18)

(11.19)

in which case we can rewrite (11.16) as

-2

+ f

= 2Q

(11.20)

Solution of this elliptic equation for

1Jr

allows the ageostrophic circulation at a

front characterized by a given

Q, to be obtained.

The formulation of (11.16) and (11.20) provides insight into the vertical circula-

tion at a front under hydrostatically and geostrophically balanced conditions.

For

example, Fig. 11.7 represents a case where frontogenesis is being forced by the

confluence mechanism (Fig. 11.6a). Convergent geostrophic flow in the x-direc-

tion is advecting warm and cold air toward each other. The required ageostrophic

circulation given by (11.20) is indicated qualitatively by the streamline. The physi-

cal sense

ofthis

solution is seen as follows. In the illustrated confluence case, b, >

0, u

< 0, and by =

Hence, according to the definition

(ll.ll),

Q, >

follows

from (11.17) that the geostrophic wind is acting to

strengthen the horizontal tem-

perature gradient. At the same time, the positive value of

QI in the y-component of

(11.12) acts to

weaken the vertical shear of the along-front geostrophic current.

Thus, the Q-vector component

acts to destroy the along-front part of the

thermal-wind balance (11.6). As always in quasi-geostrophic flow, the role of the

ageostrophic circulation is to compensate this destruction in order to maintain the

thermal-wind balance.

The

two terms on the left-hand side of (11.16) must to-

gether exactly counteract the tendency of

Q, to destroy thermal-wind balance. In

the illustrated solution in Fig. 11.7, the ageostrophic circulation

w) has the

characteristics

< 0 and Wx > 0, except on lower and upper boundaries. (11.21)

This effect of

> 0 is to counteract the effect of

in (11.17) through differential

adiabatic temperature changes. The adiabatic cooling and warming associated

with the upward and downward components, respectively, of the ageostrophic

circulation act to weaken the buoyancy gradient at middle levels. Consequently,

the horizontal thermal gradient at midlevels does not become as strong as at lower

and upper levels. At those levels

w (and, hence, w

)

are zero. Therefore, the

thermal wind balance is maintained at lower and upper boundaries (e.g., the

(11.23)

11.2 Circulation at a Front

453

ground and the tropopause) entirely by the horizontal component of the ageo-

strophic circulation, which everywhere in the example of Fig. 11.7 has vertical

shear such that

uaa

> 0

(11.22)

which counteracts the effect of

in the along-front component of (11.12). The

Coriolis acceleration of the horizontal component of the ageostrophic circulation

thus acts to strengthen the vertical shear of the along-line geostrophic wind.

At lower and upper boundaries, (11.22) is the only effect mitigating the destruc-

tion of thermal wind balance. Adiabatic temperature changes are therefore absent,

and it is possible to build up very concentrated gradients of potential temperature

at the lower and upper boundaries. Given enough time, the thermal gradient on

the boundaries may collapse to a near discontinuity. Such a collapse of the low-

level field of

b in a quasi-geostrophic front of the type we have been considering is

indicated in Fig. 11.8.

11.2.2 Semigeostrophic Frontogenesis

As indicated in Fig. 11.8, quasi-geostrophic frontogenesis produces a front that is

vertically oriented. However, real frontal zones are observed to have sloping

leading edges. Another unrealistic feature, evident from Fig. 11.8, is that regions

of static instability

(aii/az

< 0) can be formed at low levels.

turns out that there

are further unrealistic features, among which is that the frontogenesis proceeds

much too slowly.

291

The major shortcomings of the quasi-geostrophic theory of frontogenesis are

traced to the fact that it does not take into account that a front is highly nonisotro-

pic, with different characteristic length and velocity scales in the along-front and

cross-front directions. To take these differences in scale into account we make use

of the semigeostrophic theory summarized in Sec. 2.2.2. The equation of motion

for the along-front component of the wind is (2.30). Recall that the total derivative

operator in the semigeostrophic system.

(DAIDt)

includes advection by the ageos-

trophic component of motion

(ua,w) as well as by the geostrophic flow (ug,V

g).

Thus, the First Law of Thermodynamics (2.11) in the semigeostrophic system is

DAb = 0

The form of the semigeostrophic momentum and thermodynamic equations

(2.30) and (11.23) can be simplified by a coordinate transformation in which a new

cross-front coordinate is defined as

X=x+~

291 See Bluestein (1986) for further discussion.

(11.24)

(11.26)

454

11 Precipitating Clouds in Extratropical Cyclones

From (2.110), it is seen that X is related to the absolute momentum M. Specifi-

cally,

x =

(11.25)

where M

is the value

M computed with the geostrophic wind

VI('

According to

(2.30) and the coordinate transformation (11.24), the wind in the new coordinate

system, obtained by applying the total derivative operator

DlDt

[defined by (2.2)]

to (11.24), is the geostrophic wind:

-=u

Dt g

Using the transformation from x to X, we can recover the simple geostrophic

form of the basic equations. Consider an arbitrary quantity

.91

=.91

(X,y, a,t)

(11.27)

Taking

D(l1.27)lDt, applying the chain rule of differentiation, substituting from

(11.26), and recalling that the wind component in the y-direction is geostrophic

yields

where

D.91

:tJ.91

a.91

--=--+w-

:tJ-r

(11.28)

:tJ

a a a

-;:

-+u

- (11.29)

:tJ-r

a-r

g ax g

and the notation

a/aT

and a/az is used to indicate that X (not x) is being held

constant in the differentiation; that is,

(11.30)

Applying (11.28) to

= V gand b, and noting from (2.30) and (11.23) that Dv g/Dt =

DAvg/Dt =

-Ju

and

Db/Dt

= DAb/Dt = 0, we obtain

:tJv

:tJ: +

= 0 (11.31)

and

where

:tJb

-+W-=O

:tJ-r

waV

;:--+u

a J

(11.32)

(11.33)

11.2 Circulation at a Front 455

By comparing (11.31) and (11.32) to the y-component of (2.23) and (11.9), the

similarity in form to the quasi-geostrophic equations can be seen.

Before proceeding, it is useful to note some further properties of the geo-

strophic coordinate transformation. By the chain rule of differentiation,

and

Taking

il(11.24)/ilx, we obtain

a.s4.

-=--

a.s4. a.s4.

a.s4.

-=--+-

c.;

ax f

(11.34)

(11.35)

(11.36)

where

'ag

is the vertical component of the geostrophic absolute vorticity, as de-

fined by (2.65). Since the geostrophic flow is invariant in y, according to our

assumptions,

(11.37)

Taking il(11.24)/il

we obtain

With substitution from (11.36)-(11.38), (11.34) and (11.35) become

a.s4.

-=--

ax f

and

a.s4. a.s4.

a.s4.

-=---+-

In the special case where

.s4.

= v

, (11.39) becomes

'ag

-=--

ax f

and, with the aid

(11.41), (11.40) becomes

g =

'ag

(11.38)

(11.39)

(11.40)

(11.41)

(11.42)

456 11 Precipitating Clouds in Extratropical Cyclones

The identities (11.34)-(11.42) are useful in converting several of the basic equa-

tions from

x to X space. First, it can be seen that the thermal-wind relation retains

its form in

X space. If.stl = b, then from (11.39) we have

'ag

- =

(11.43)

dx f dX

From (11.42) and (11.43) and the thermal-wind equation in x-space (11.6), we

obtain

= b

(11.44)

which is analogous to the along-front part (i.e., the y-component) of (11.6).

follows from the thermal-wind balance (11.44) that there exists a function

that satisfies relations of the form

(11.45)

(11.48)

and

b =

C'i>z

(11.46)

which are analogs to the geostrophic and hydrostatic relationships in x-space

[(2.68) and (11.5)].

can be seen, moreover, that the function

C'i>

---.!..

(11.47)

where

is the geopotential.v" Thus, if

is used instead of

<1>,

the forms of the

geostrophic and hydrostatic relationships are preserved in X-space.

The identities

(11.39)-(11.42) can be further used to show that the form of the

mass-continuity equation is also preserved in the X-coordinate system, if we

define new velocity components. If we use the ageostrophic component

Us,

defined in

(11.33), and define a new vertical-velocity component

W=w

then the continuity equation (11.18) can be rewritten, with the aid of (11.39) and

(11.40), as

--+-0::0

dX dZ

(11.49)

A particularly useful quantity in the context of the X-coordinate system is

IJ'.=-CI)

.v»

g f ag

(11.50)

292 To show that

1.47) satisfies

1.45) and

1.46), one must simply differentiate

and make use

of (2.68), (11.5), (11.39), and (11.40).

11.2 Circulation at a Front 457

where

Wag

is the geostrophic absolute vorticity, defined in x, y, and z coordinates

by (2.65).

is defined in pseudoheight coordinates as

(11.51)

(11.52)

The quantity

I!P

g is similar to the geostrophic Ertel's potential vorticity given by

(2.64), and for the remainder of the chapter we will refer to

I!P

Ii simply as potential

vorticity. In the case of two-dimensional-?' flow

(a/ ay = 0), it can be shown with

substitution of (11.39) and (11.40) into (11.50) that

I!P.

= 'ag

g /

Substituting this form of

I!P

g into (11.32), we obtain

(11.53)

From (11.52) and (2.98), it is apparent that the potential vorticity has the form of a

buoyancy frequency in X-coordinates. Comparing (11.53) to the quasi-geostrophic

form of the thermodynamic equation (11.9), we see that the potential vorticity

indeed plays the role

buoyancy frequency in the thermodynamic equation in the

X system. Additionally, the potential vorticity

I!P

g has the important property that

it is conserved following parcels of air:

--=0

(11.54)

(11.55)

This conservation property is obtained for the two-dimensional, semigeostrophic,

adiabatic, inviscid case considered here by taking

D(11.52)/Dt and making use of

(11.41) to obtain

D'ag

';g

'ag Db

--=-b

--+---=-b

--+---

Dt / z Dt / Dt

Z Dt / Dt

can

be shown that the two terms on the right-hand side of (11.55) cancel by

substituting from the equation

motion (11.31) and thermodynamic equation

(11.53) and making use

mass continuity (11.49), thermal-wind balance for v

[as

expressed by (11.44)] and u

[as given by the x-component of (11.6)], the assump-

tion

no y-variation (a/ay = 0), and the nondivergence of the geostrophic wind

[seen from (2.68)]. The usefulness of (11.54) will be seen below, as we explore the

nature of the ageostrophic circulation in X-space.

293 Note that by making an additional coordinate transformation, Y = y -

(u.lf)

, we could have

shown (11.52) to be valid also for three-dimensional flow.

458 11 Precipitating Clouds in Extratropical Cyclones

By analogy to the quasi-geostrophic case, we can perform further operations on

(11.31) and (11.53) to obtain

(11.56)

and

(11.57)

where

is defined the same as

in (11.11), but with X replacing x. Equations

(11.56) and (11.57) are analogous to the y-components

(11.10) and (11.12), and

subtraction of (11.57) from (11.56) leads to

(11.58)

Since

U; and

Wobey

mass continuity according to (11.49), we can employ a new

stream function

0/',

such that

(Va'

(-p

)

Substituting this stream function into (11.58), we obtain

(

t +

pzz = 2Q,

(11.59)

(11.60)

This relation-?' is similar in form to the quasi-geostrophic ageostrophic stream-

function equation (11.20) in physical space, except that

x has been replaced by X

and the potential vorticity

rzp

g has replaced the buoyancy frequency

N2.

As long as

rzp

g is positive, (11.60) remains an elliptic partial differential equation, meaning that

it has a unique solution everywhere within the

X-Z

domain, if values on the

boundaries

the domain are given.F" Since

rzp

g > 0 is also the condition for the

flow to be symmetrically stable [Sec. 2.9.1, Eq. (2.150)], it becomes evident that

(11.60) has such a solution as long as the flow is symmetrically stable. If

rzp

g < 0

(i.e., the flow is symmetrically unstable), (11.60) is no longer elliptic.

From the similarity of (11.20) and (11.60), it is inferred that the semigeostrophic

frontogenesis forced by the confluence mechanism in X-space would have the

circulation shown in Fig. 11.9a, which is similar to that for the case of geostrophic

frontogenesis illustrated in Fig. 11.7. Recalling from (11.30) that

(ax/aZ) is defined

(ax/aa) at constant X, we note from the definition (11.24) that

axl

! (11.61)

x f

Thus, the stronger the shear along a surface of constant X, the more the surface

tilts. Hence, the circulation in Fig. 11.9a becomes skewed as shown in Fig. 11.9b

294 Sometimes called the

"Sawyer-Eliassen"

equation in honor of its developers, J. F. Sawyer

(1956) and A. Eliassen (1959, 1962).

295 See Hildebrand (1976, p. 417).