Houze Robert A., Jr. Cloud Dynamics

Подождите немного. Документ загружается.

10.3 Basic

Hurricane

Dynamics 419

First Law of Thermodynamics (2.6). The quantity

It is defined as

(10.3)

Its differential is seen to be

(10.4)

(10.6)

(10.10)

from which it follows that

a~ a~

= T (10.5)

s p

Since the partial derivative of the first expression with respect to S must equal the

partial derivative of the second expression with respect to

p, we obtain

aal

aTI

p =

It follows from the definition of the saturation equivalent potential temperature

()es

in (2.146) that

cpT

din

0es

= cpT

din

Ldqvs - LqvsT-1 dT (10.7)

The last term is negligible, and this expression may be rewritten as

cpT d In

0es

T dS (10.8)

Thus, lines of constant B

above the boundary layer in Fig. 10.15 may be regarded

as lines of constant saturated moist entropy.

Since it has been assumed that the value of

on an msurface is equal to the

value of

where the msurface intersects the top of the boundary layer, we may

write

S = c

fern

only) = c

~(h),

on an msurfaceat z

h (10.9)

Expressing the field of mean specific volume a as a function of

and

obtain

alii

ami

alii

ami

aTI

p =

p' dm =

m din

The expressions on the right follow from (10.6) and the condition that a surface of

constant moist entropy

is also a surface of constant

With

amlar

given by

(10.10) and

ami

by the thermal wind equation (2.42), the slope of the m surface

(10.1) becomes

arl

aTI

----

m 2m din

(10.11)

420 10 Clouds in Hurricanes

Integrating (10.11) along an msurface from some arbitrary radius r to r =

00,

obtain

lIdS

- =

--[T

-T

(p)]

m diii 0 m

(10.12)

where Tm(p) is the temperature on the m surface at pressure p and

is the

outflow temperature on the

m surface (i.e., the temperature at r =

00).

Since it is

assumed that the hurricane has adjusted to a state of conditional symmetric neu-

trality,

Tm(p) is given by the temperature along the saturation moist adiabat corre-

sponding to

In using (10.12) to construct the fields of mand ii.

throughout the

region above the boundary layer, we need the radial distributions of

and ii. at

the top of the boundary layer (z

= h). These distributions determine

dSldm,

according to (10.9), and give us a point on the m surface from which to integrate

the saturated moist-adiabatic lapse rate to obtain

Tm(p).

remains to make some

assumption about the value of

To; we will return to this question. First, we seek

the radial distributions of

and ii. at z = h.

An assumption is made, on the basis of observations, that the temperature at

the top of the boundary layer is a constant

Te-

In this case, (10.12) applied at the

top of the boundary layer is

(To

- T

)

m dm = 1, Z = h (10.13)

Since

as/ar

-=--

dm am/ar

(10.14)

(10.13)

may be written as

(To

Tn)r

=:r (

~').

z = h (10.15)

Substitution from the equation of state (2.3), the gradient-wind equation (2.36),

and (10.9) changes (10.15) to

-T

alne

= R

~(lnp+~

alnp)+~

z = h (10.16)

ar c

ar 2 ar

2cp~

which gives us a relation between ii. and p at z = h if we integrate once in r. The

integration is carried out from some distant radius

r-,

which represents the outer

boundary of the storm, where

ii. = B

at z = h to an arbitrary radius r within the

storm. The integration is made difficult because

is a function of mand therefore

r. The following definition of a mean outflow temperature is used to simplify the

problem:

(10.17)

(10.18)

(10.21)

10.3 Basic Hurricane Dynamics 421

This quantity turns out to be an insensitive function of r and is treated as a

specified constant. Then integration of (10.16) gives

- T

Oe(r) R

p(r)

c)Inp(r)

---"-----'~

-In

+ - -

-,------

(}ea

o; c

+L(r

-r,n,

z = h

which is one relation between iJe(r) and

p(r)

at the top of the boundary layer.

At the center of the storm, where

r = 0 and a In

plar

= 0, (10.18) becomes

c (f T) (j

In Pc = p 0 - B

In~

+~,

z = h (10.19)

RdT

(}ea

dTB

where subscript c indicates the center of the storm. Since

- T

is negative, this

relation implies a linear proportionality between the central pressure deficit of the

storm and the equivalent potential temperature excess in the eye of the storm. The

implied relationship agrees well with data in hurricanes and thus adds confidence

to the applicability of

(10.18).

If iJe(r) at the top of the boundary layer can be determined independently, then

p(r)

at z = h will be determined by (10.18), and

m(r)

will follow from the gradient-

wind equation

(2.36). Independent determination of iJe(r) at the top of the bound-

ary layer is obtained by quantifying the boundary-layer model represented sche-

matically in Fig.

10.15.

The boundary layer may be considered in terms of a quantity stl that is con-

served (like

and m) in laminar inviscid flow. Under turbulent conditions,

.sa

governed by a mean-variable equation of a form similar to (2.78), (2.81), and

(2.83). In the Boussinesq case (which is suitable for the boundary layer), the

density factor

in those equations is not present, and the equation for

.sa

may be

written in axisymmetric cylindrical coordinates as

- I

a~A

stl +ustl

+wd

---

(10.20)

t r z

where

is the vertical eddy/flux of

as defined for the examples in (2.186)-

(2.189).

If we now assume that the storm is in a steady state

(.sal

= 0) and the

boundary layer is well mixed

(.sa

= 0), then the vertical eddy-flux convergence

just balances the radial advection and

(10.20) may be integrated over the depth of

the boundary layer (from

z = 0 to h) to obtain

a;:-

l/I(h) = r[

(h)

(0)]

where we have made use of the two-dimensional stream function

(10.22)

422 10 Clouds in Hurricanes

which satisfies the mean-variable form of the anelastic continuity equation (2.54)

in cylindrical coordinates, with

p as the density weighting factor. The value of

l/J

has been set to 0 at z =

The surface flux

over

the ocean, represented by term

TA(O)

in (10.21), can be

calculated from the bulk aerodynamic forrnula-"

1"A(O)

-pCAlvl(sd

-sd

SFC

)

(10.23)

where v is the tangential component, sd

is the value of di in the well-mixed

boundary layer,

SFC

is the value of di at the sea surface, and C

is an empirical

coefficient.

For

sd = c

In Be, (10.23) becomes

1"s(O)

-pcpcslvl[ln

e;,(h)

-In

(SST )] (10.24)

where Bes(SST) is the saturation equivalent potential temperature calculated at the

sea-surface temperature (SST).

For

sd = m, (10.23) becomes

(10.25)

where the notation

CD stands for drag coefficient, and substitution for m from

(2.35) has been made to obtain the last expression on the right. The sea-surface

temperature enters the calculations as a crucial specified quantity in (10.24).

through the surface flux of

that the storm obtains its energy. In region II of the

boundary layer, where fluxes at

h are negligible, (10.21) for di =

and

iii

becomes,

with substitution from (10.9), (10.24), and (10.25),

alne;,

I-If

- ]

lfI(h)

Cp-----a;-

lfI(h)

= rpcpC

In8

e(h)-ln

~s(SST)

(10.26)

and

ami

I-I~

a;:

lfI(h)

V V

Since

jaml

(10.26) divided by (10.27) gives us

= (CScp/CDrv)

In[Oe

(h)/8

(SST)]

Substitution of this expression and (2.35) into (10.13) leads to

(-2

)

In 8

= In 8

(SST) - ( ) v +

z = h

Csc

276 See Roll (1965, p. 25\).

(10.27)

(10.28)

(10.29)

(10.30)

10.3 Basic Hurricane Dynamics 423

When this expression is substituted into (10.18) for In

and Ii is expressed in

terms of radial pressure gradient by means of the gradient-wind equation

(2.36),

(10.18) becomes a differential equation for per) at z = h in region II. Thus, (10.18)

and (10.30) form a set of simultaneous equations for

and p at the top of the

boundary layer in region II.

Equation

(10.30) was derived assuming that the fluxes at the top of the bound-

ary layer

[TA

(h)]

are negligible in region II. That such an assumption is inappro-

priate for region III can be seen from the ratio

Oe!Bes(SST)

implied by (10.30). This

ratio is directly proportional to the surface relative humidity.

277

can be seen

from

(10.30) that In 0" and hence the surface relative humidity, is a minimum at

the radius of maximum wind, implying that the relative humidity would increase

with increasing radius (and decreasing

Ii) in region III. Observations indicate that

the surface relative humidity is approximately constant in hurricanes, with a value

of about

80%. This result evidently is not given by (10.30) because the eddy flux at

the top of the boundary layer was set equal to zero. In region III, strong down-

drafts are associated with convection in rainbands. These drafts evidently contrib-

ute strongly to the fluxes at the top of the boundary layer and thus keep the

relative humidity lower than predicted by

(10.30).

Therefore, outside the radius of maximum wind (i.e., in region III) the bound-

ary layer is parameterized simply by setting the surface relative humidity empiri-

cally to a constant value of

80%. The radius of maximum wind is then that radius

at which the relative humidity in region II, implied by

(10.30), reaches 80%, and

the value of

in the boundary layer outside this radius is the value corresponding

80% relative humidity. Use of this value of

in (10.18) then gives an equation

for

per) at z = h in region III, which matches that in region II at the radius of

maximum wind. Since

(10.30) determines per) in region II,

Oe(r),

and mer) at z = h

can now be calculated throughout regions II and III. [The value of mer) is deter-

mined from

per) and the gradient-wind equation (2.36).] Since these quantities are

known at z

= h, (10.12) can be solved for the msurfaces above the boundary layer,

and according to

(10.9) the m surfaces can also be labeled as Ssurfaces corre-

sponding to the value of

at z = h at the radius where they intersect the boundary

layer. Thus, the streamlines within the eyewall cloud can be constructed if the

sea-surface temperature SST, the outflow temperature

To, the ambient surface

relative humidity

(80% in the above discussion), and several less critical

quantities

(!,

Po,

rs,

Cs/C

and T

)

are specified.

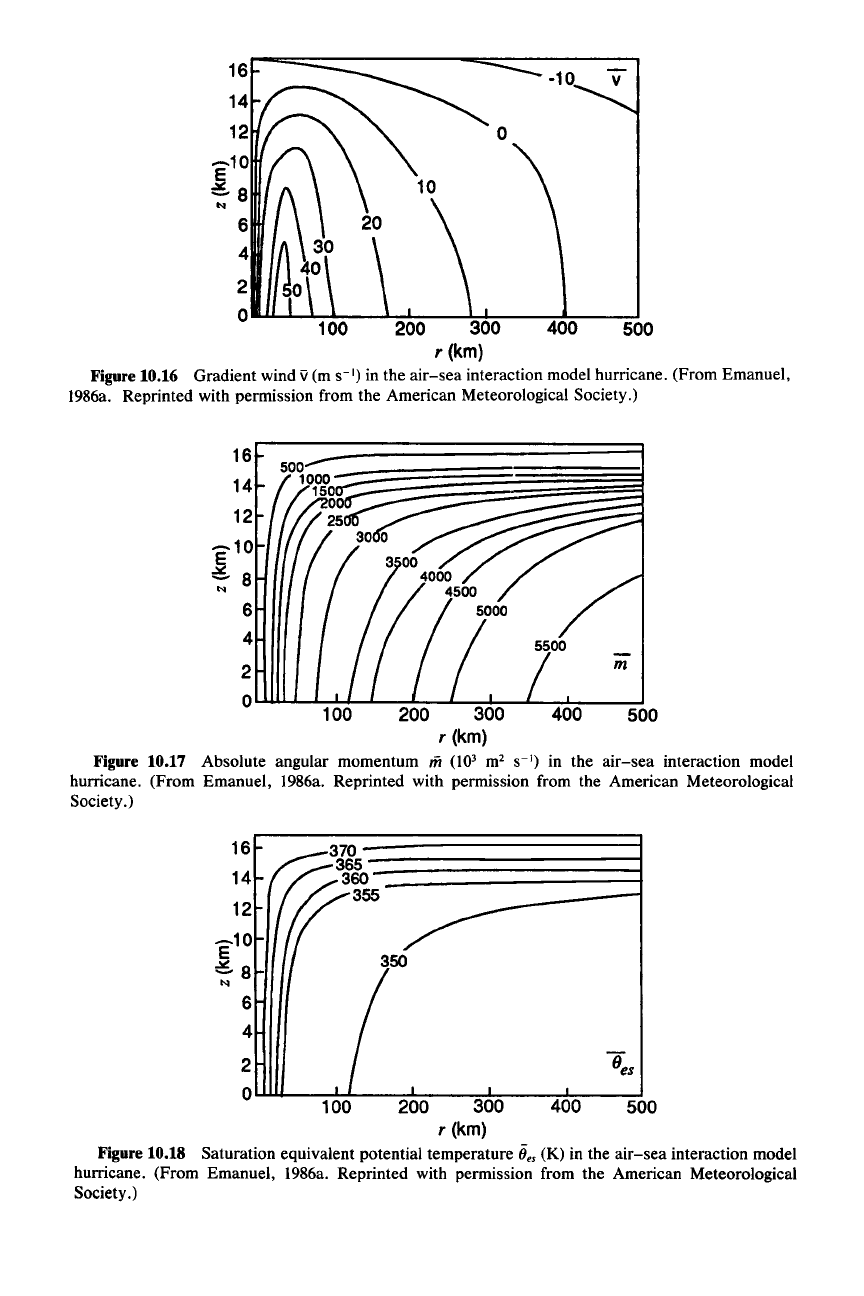
The results of an example of this type of calculation are shown in Figs.

10.16-

10.19 for a case in which the sea-surface temperature SST = 300 K, T

= 295 K,

To = 206 K, RHo = 80%,f(cP) =

!(28°),

Po = lOIS mb,

= 400 km, and C, = CD.

The central pressure of the model storm is 941 mb, and the maximum tangential

wind component is

58 m

S-I.

To obtain these results, the region II boundary-layer

model was assumed to extend into the eye (region

1). The solutions in region I are

thus not reasonable since in region I the gradient wind balance

(2.36) does not hold

there. This procedure was adopted only for convenience. Since our main purpose

in this chapter is to gain some insight into the nature of the air motions in the

277 See Emanuel (l986a) for details.

500

400

................

"""""'":~-"""""'":~----'.::+=--~~-~

300

(km)

Figure 10.16 Gradient wind Ii (m

S-I)

in the

air-sea

interaction model hurricane. (From Emanuel,

1986a. Reprinted with permission from the American Meteorological Society.)

500

400

1Sr----=====================t

-10

'&a

0~..L..l-...L.:-~.....L..--=~.....L.."""":"::!-=-.....L..~:!-=-_~

300

(km)

Figure 10.17 Absolute angular momentum m (10

S-I)

in the

air-sea

interaction model

hurricane. (From Emanuel, 1986a. Reprinted with permission from the American Meteorological

Society.)

500

400

200

350

u.u'-----:~

___::~

_ ___::+=

~~~~

1Sr---:;;~================1

-10

300

(km)

Figure 10.18 Saturation equivalent potential temperature ii" (K) in the

air-sea

interaction model

hurricane. (From Emanuel, 1986a. Reprinted with permission from the American Meteorological

Society.)

10.4 Clouds and Precipitation in the Eyewall

425

hurricane's clouds, which occur only in regions II and III, the inadequate treat-

ment of the eye dynamics is not a serious deficiency. The primary vortex circula-

tion is shown by Fig. 10.16. The distribution of maximum winds in the eyewall

resembles that seen in Fig. 10.7, although the winds are stronger in the calculated

case than in the composite section, where averaging from many cases has smeared

the basic pattern. The

Iii and B

surfaces in Fig. 10.17 and Fig. 10.18 may be

regarded as the streamlines

the flow above the boundary layer. The upward and

outward flow demanded by the conservation of

Iii is clearly evident from these

cross sections. That the upward flow is highly concentrated in the eyewall region

is indicated by Fig. 10.19, where the vertical velocity at the top of the boundary

layer implied by the stream function in (10.26) and (10.27) is seen to have a strong

maximum in an annular zone corresponding to the eyewall.

The theoretical picture

just

developed has been further examined by numerical

model simulations, which use a nonhydrostatic cloud model of the type discussed

in Sec. 7.5.3. The model is adapted to the hurricane by formulating it in cylindrical

coordinates and making it two-dimensional by assuming uniformity in the azi-

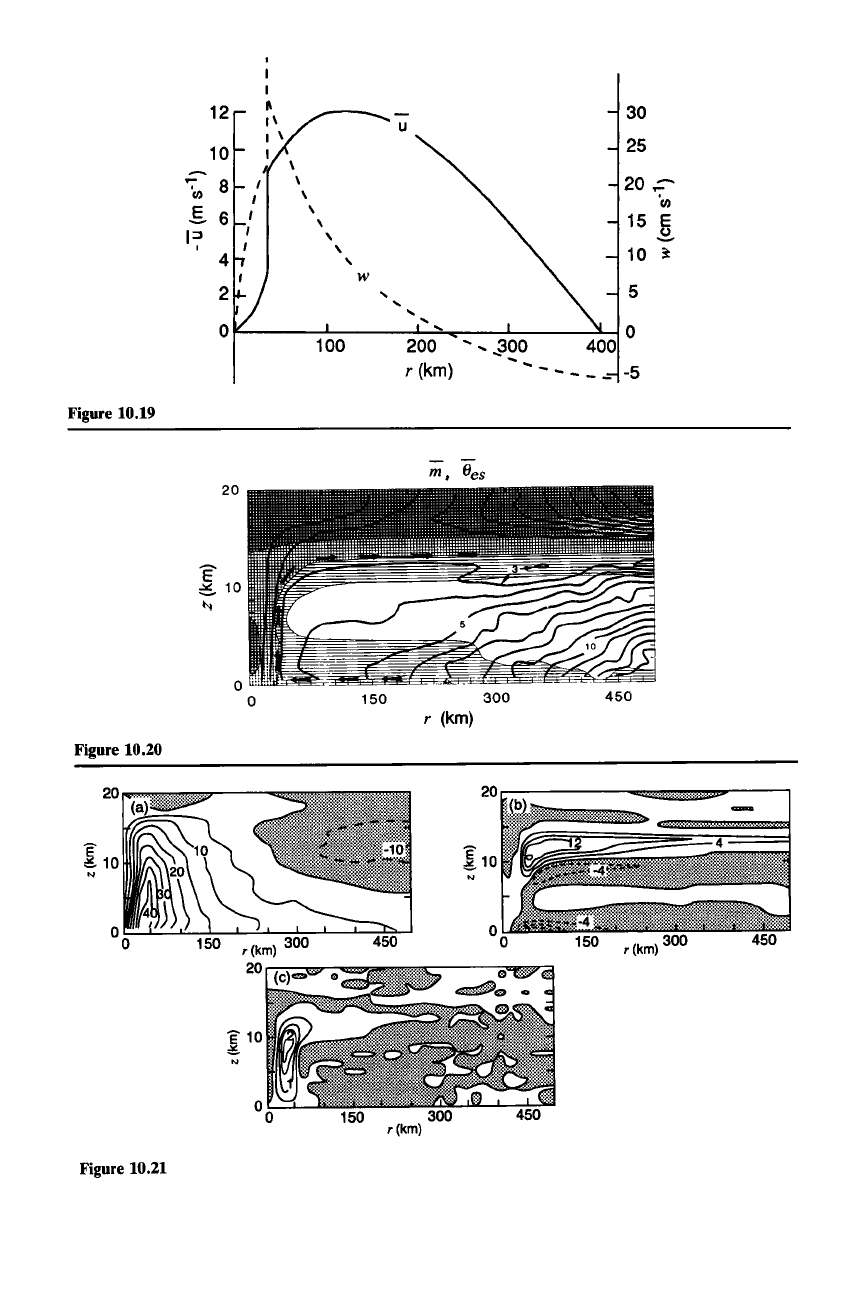
muthal direction. Results from such a model are shown in Fig. 10.20. In this

particular calculation, the undisturbed environment was assumed to be neutral to

conditional instability but unstable in the conditionally symmetric sense. This

assumption represents real hurricane environments fairly well, except that the

latter are not actually neutral but characterized by a small degree of conditional

instability. The numerical experiment was meant to minimize the role of vertical

convection in the development

ofthe

storm. The idea was to see if storm develop-

ment could take place without a conditionally unstable environment. The result

was a rather realistic hurricane vortex. As we will see below, this model storm

was similar to model storms simulated with conditionally unstable environments

and resembles observations of intense hurricanes reasonably well. In Fig. 10.20it

can be seen that, after the model storm became well developed, streamlines in the

eyewall region were parallel to the

Iii and S surfaces. Thus, it is evident that the

eyewall region of the model storm developed as a conditionally symmetrically

neutral circulation connected to a boundary layer in contact with the warm sea

surface.

10.4 Clouds and Precipitation in the Eyewall

10.4.1 Slantwise Circulation in the Eyewall Cloud

As always in this book, our objective here is to gain insight into the air motions

associated with clouds and precipitation. Since, in the hurricane, the clouds are

mainly associated with the eyewall and the rainbands, we devote the last two

sections

ofthis

chapter to these components of the storm. In this section we focus

on the eyewall. Then in Sec. 10.5 we will examine the rainbands.

We begin our discussion of the eyewall clouds by returning to the observations

of the inner-core region of the hurricane (Figs. 10.13 and 10.14) to compare them

E 10

150

300

450

r (km)

Figure 10.20

110

10;;

150

r(km) 300

450

I \

20 .::-

'I/)

1::::1

.2-

...

100

200

,3~0

400

r (km)

'--

---

-5

Figure 10.19

Figure 10.21

10.4 Clouds and Precipitation in the Eyewall 427

to the theoretical picture developed in Sec. 10.3 (Figs. 10.15-10.20). We have

already noted that at the top of the boundary layer the strong vertical velocity in

the theoretical circulation is concentrated at the location of the eyewall cloud (Fig.

10.19). Airborne Doppler radar observations, such as those illustrated in Fig.

10.13, also show the strong narrow updraft maximum in the eyewall. In addition,

the radar observations indicate that the upward flux occurs in a slantwise pattern.

Thus, the vertical mass transport in the eyewall cloud appears to be dominated by

the momentum-conserving flow described by theory. Further consistency is seen

in the upper-level radial outflow, which in both the theoretical and observed cross

sections occurs in a concentrated layer aloft. The radial outflow is an important

feature

ofthe

cloud and precipitation pattern since it spreads ice particles outward

and thus accounts for the stratiform precipitation region lying typically just out-

side and adjacent to the eyewall convection. The strong tangential circulation

predicted by theory also agrees well with the observed primary circulation, which

in the context of the clouds and precipitation is important in distributing ice

particles around the storm (Fig. 10.14).

10.4.2 Strength of the Radial-Vertical Circulation in the

Eyewall Cloud

The comparisons made in Sec. 10.4.1 show

qualitatively that the air motions

observed in the eyewall region are generally similar to those computed from the

theory of the symmetrically neutral circulation connected to the well-mixed

boundary layer over the warm sea surface. We now explore the nature of the

eyewall motions

quantitatively by inquiring about the strength of the radial-verti-

cal circulation responsible for determining the structure of the eyewall clouds and

precipitation. We proceed by examining the results of both model simulations and

data. We saw at the end of Sec. 10.3 that, when adapted to the hurricane, the

nonhydrostatic cloud model of the type discussed in Sec. 7.5.3 produces a mature

vortex with a conditionally symmetrically neutral eyewall circulation (Fig. 10.20).

A few more results of this simulation are shown in Fig. 10.21. In addition, Fig.

Figure 10.19 Radial distribution of vertical velocity w (ern

S-I)

at the top of the boundary layer and

mean radial velocity (j (m

S-I)

within the boundary layer in the

air-sea

interaction model hurricane.

(From Emanuel, 1986a. Reprinted with permission from the American Meteorological Society.)

Figure 10.20 Results of a two-dimensional nonhydrostatic numerical-model simulation of a

hurricane. Fields were averaged over a 20-h period in which the storm was approximately steady.

Shading indicates equivalent potential temperature values of 345-350 K (horizontal lines), 350-360 K

(medium shading), and >360 K (heavy shading). Absolute angular momentum is shown by contours

labeled in nondimensional units. Also indicated is the airflow through the updraft. (From Rotunno and

Emanuel, 1987. Reprinted with permission from the American Meteorological Society.)

Figure 10.21 Results of a two-dimensional nonhydrostatic numerical-model simulation of a

hurricane. Fields were averaged

over

a 20-h period in which the storm was approximately steady. (a)

Tangential, (b) radial, and (c) vertical wind components (m

S-I)

are shown. Negative values of fields

are indicated by shading. (From Rotunno and Emanuel, 1987. Reprinted with permission from the

American Meteorological Society.)

428 10 Clouds in Hurricanes

Figure 10.22 Results of a two-dimensional nonhydrostatic numerical-model simulation of a

hurricane. Fields shown are (a) tangential, (b) radial, and (c) vertical wind components (m

S-I).

Negative values of fields are indicated by shading. (From Willoughby et al., 1984a. Reprinted with

permission from the American Meteorological Society.)

10.22 contains results from a similar model for a simulation in which the ambient

environment is not restricted to neutrality or to conditional symmetric instability,

but rather is conditionally unstable. Despite this difference in large-scale environ-

ment, the model results are remarkably similar, indicating again that the eyewall

dynamics are dominated by the slantwise motions. Both model simulations show

maximum vertical motions in the eyewall (Figs.

1O.21c

and 10.22c)

00-5

m s

radial outflow aloft (Figs.

1O.21b

and 10.22b) is concentrated into an eyewall

detrainment layer between 10 and 14 km in height, where

u reaches values of

15-

20 m

S-I.

These model results agree well with data from aircraft penetrations of hurricane

eyewall regions. There are two principal types of data: flight track data obtained

in situ measurements made from the aircraft, and data from Doppler radar,

airborne, which provides measurements in a large volume of space surrounding the

flight path. Flight track data of the vertical velocities in the eyewall of an intense

hurricane are shown in Fig. 10.23. Vertical velocities determined from the hori-

zontal wind data by integrating the anelastic continuity equation (2.54) are shown

in Fig. 10.23a, while Fig. 10.23b shows vertical velocities derived from measure-

ments made with the inertial navigation system of the aircraft. Peak magnitudes of

just over 6 m

S-l

are indicated by both types of measurement. Figure 10.24 shows

that these vertical velocities are typical of those seen at flight level in other

hurricanes. These values are slightly, though probably not significantly, larger

than the values indicated by the model calculations. Vertical velocity observa-

tions by Doppler radar aboard an aircraft flying through another intense storm are

shown in Fig. 10.25a. These data also show vertical velocity peaks (the largest

S-I)

somewhat stronger than in the models or the other aircraft data. These