Houze Robert A., Jr. Cloud Dynamics

Подождите немного. Документ загружается.

(5.20)

5.2 Stratus, Stratocumulus, and SmaU Cumulus in Boundary Layer Heated from Below 159

where

w(h)

is the mean vertical velocity

ofthe

air at z = h (i.e., the rate

change

height associated with

net

horizontal convergence or divergence in the mixed

layer), while

is the entrainment velocity, or the rate at which less dense,

laminar air is incorporated into the denser, turbulent layer. Typically, the cloud-

topped

boundary

layer

is divergent so

that

w(h)

< 0, while the entrainment veloc-

ity is positive as the

boundary

layer grows by incorporation

air from above.

According to (2.16)

and

(5.18), calculation

averages qr and

within the layer

z = 0 to h yields the vertical distribution

the horizontal averages q

q,.,

and Bin

the cloud, since the cloud layer is saturated and nonprecipitating.

is therefore

useful to

seek

the predictive equations for qr and

Be.

The

equation for qr is

obtained from the Boussinesq version

the mean-variable form of the water-

continuity equation (2.8I), for the

case

in which there is only one category of

water

substance

(qr =

q;)

and the sources and sinks

are all zero. The Bous-

sinesq assumption implies

that

the density terms do not

appear

in (2.8I). There are

no horizontal or vertical advection terms since

qr varies neither horizontally nor

vertically.

The

total derivative

D/Dt

in (2.8I) simplifies to d/ dt, and (2.8I) reduces

dqT

(-,-,)

=--

wqT

By similar reasoning, the equation for

is obtained from the Boussinesq version

the mean-variable form

the First

Law

of Thermodynamics (2.78). Both

radiation and the latent

heat

phase

change (condensation or evaporation) are

included in the heating-rate

term

'Ie

(2.78).

The

horizontal and vertical advec-

tion terms again

are

zero.

Thus,

(2.78) may be written as

)

e =

w'9'

\5Jt

(5.21)

(5.22)

where the

overbar

represents a horizontal average, the primed terms are turbulent

fluctuations away from the average, and

\5Jt

is the

net

radiative flux, as in (5.4). We

have written (5.2I) in terms

On so

that

\5Jt

is the only heat source/sink that

appears explicitly.

Since, according to the mixed-layer assumption,

qr and

are constant in

height, (5.20) and (5.2I) imply

that

(w'

qT)

= constant, 0 s z s h

and

~(w'9;

\5Jt)

= constant, 0 s z s h

The

water

and

heat

fluxes at the

earth's

surface are denoted by

(

w'q' )

==;yi;

ToTo

(5.23)

(5.24)

160 5 ShaDow-Layer Clouds

and

(w'o;t

(5.25)

The turbulent fluxes at the top of the mixed layer are assumed to be responsible

for diluting the average values of

ar and ()e within the mixed layer. Since the net

rate of dilution is determined by the rate at which air from the layer above the

mixed layer (whose values of

and

()e

differ from those in the mixed layer by

amounts

!:J.qr

and

!:J.()e)

is incorporated into the mixed layer, we may set

(5.26)

and

(W'O;)h

-weA~

(5.27)

where the subscript h indicates conditions at the top of the boundary layer.

has

already been assumed that the air entrained at rate

is instantaneously mixed

through the turbulent layer, thus maintaining constant values of

iir and if

through-

out the layer. Substituting

(5.24)-(5.27) into (5.22) and (5.23), we obtain

(5.28)

(5.29)

and

(--

)

-we

-CJF

ffi-L

ffi-

- w' 0' +

ffi-

---"-----='-------=:.::----'-'-,,---"'-

e h

which may be substituted into (5.20) and (5.21) to obtain the following predictive

equations for

iir

and if

and

(5.30)

ae,

--=

~AOe

-ffi-

ffi-

(5.31)

For our purposes, the fluxes of

and

()e

at the surface

(;giro

and

;gieo,

respec-

tively), the radiative flux difference

(ffi-h

ffi-

) ,

and the vertical velocity

w(h)

may

be considered as given.

128 In this case, (5.19), (5.30), and (5.31) form a set of three

equations with four unknowns:

iir,

if., and We' The problem reduces to deter-

mining the entrainment rate

in a physically reasonable way in order to close the

set of equations. If this can be done, then the evolution of the mixed layer, as

characterized by its height

(h),

thermodynamic structure (if

) ,

and water content

(iir), can be computed.

128 The surface flux and radiation could also be parameterized in terms of other variables. But that

extra complication is not necessary to illustrate the basic ideas of the mixed-layer model.

5.2 Stratus, Stratocumulus, and SmaU Cumulus in Boundary Layer Heated from Below

161

There are two approaches to closing the equations for the mixed layer, depend-

ing on whether they are being solved diagnostically or prognostically. In the

former case, the entrainment rate and the time derivatives are determined from

observations, and the turbulent fluxes implied by the equations are then compared

to observed fluxes. In the prognostic case, the entrainment is determined from the

turbulent kinetic energy equation, and the time derivatives are computed to deter-

mine the evolution of the boundary layer.

We will examine both the diagnostic and prognostic cases briefly. However, we

first note that in either case, we first need to split the fluxes of

qT and

into

component parts. To do this, we make use of the approximate expression for

equivalent potential temperature (2.19) and the definition of

cloud

virtual

potential

temperature,

0cv

0(1 + 0.61qv - qL) = 0v -

OqL

(5.32)

With appropriate scaling of 0 and ql" (2.19) implies that the turbulent eddy flux of

potential temperature can be approximated as

LO-

w'O' ::= w'O; -

-T

w'q~

(5.33)

For the subcloud layer, where there is no liquid water, (5.18), (5.32), and (5.33)

imply

(5.34)

w'O' = W'O' ::= W'O' -

o[~

- 0 61]

w'q'

(5.35)

veT'

In the cloud layer, the air is saturated and liquid water is present. The saturation

mixing ratio

qvs is a function of both temperature and pressure. However, it is a

much stronger function of temperature, and at a given height in the boundary layer

the pressure is nearly constant. Hence, for the cloud layer, it is a good approxima-

tion to write the vapor flux as

w'q'

::= T

w'o'

v 0

follows from (5.32), (5.33), and (5.36) that

a.,»

W U

::= T w U

where

(5.36)

(5.37)

(5.38)

- 1+ 1.61T(aqvs

faT)

-1+(L/c

p)(aqvs/

aT)

The factor

f3T

is a slowly varying function of temperature, which has a value of

about 0.5 under cloud-topped mixed-layer conditions.

162 5 Shallow-Layer Clouds

In the diagnostic case, closure of the equations is obtained from observations of

the eddy flux of total water near the top of the mixed layer

(w'q~).

The entrain-

ment velocity

is obtained simply by substituting this observed value into (5.26).

When this value of

is substituted in the right-hand sides of (5.30) and (5.31),

then

dih/dt

and dOe/dt are known and according to (5.20) and (5.21) imply the

vertical distributions of the fluxes

(w'q~)

and (w'O; +

!Jt).

If a profile of the

radiative flux

!Jt

is assumed, then the equations imply values of w'

and w'

0;.

these fluxes are further decomposed according to (5.33)-(5.37), we obtain the

profiles of

w'O',

w'O~,

q~,

(w'O;),

(w'

q~),

and

(w'

q;,). Thus, the equations for the

mixed layer are used to diagnose the turbulent fluxes from measurements of

tiO

tiqT, h, and w'

at h.

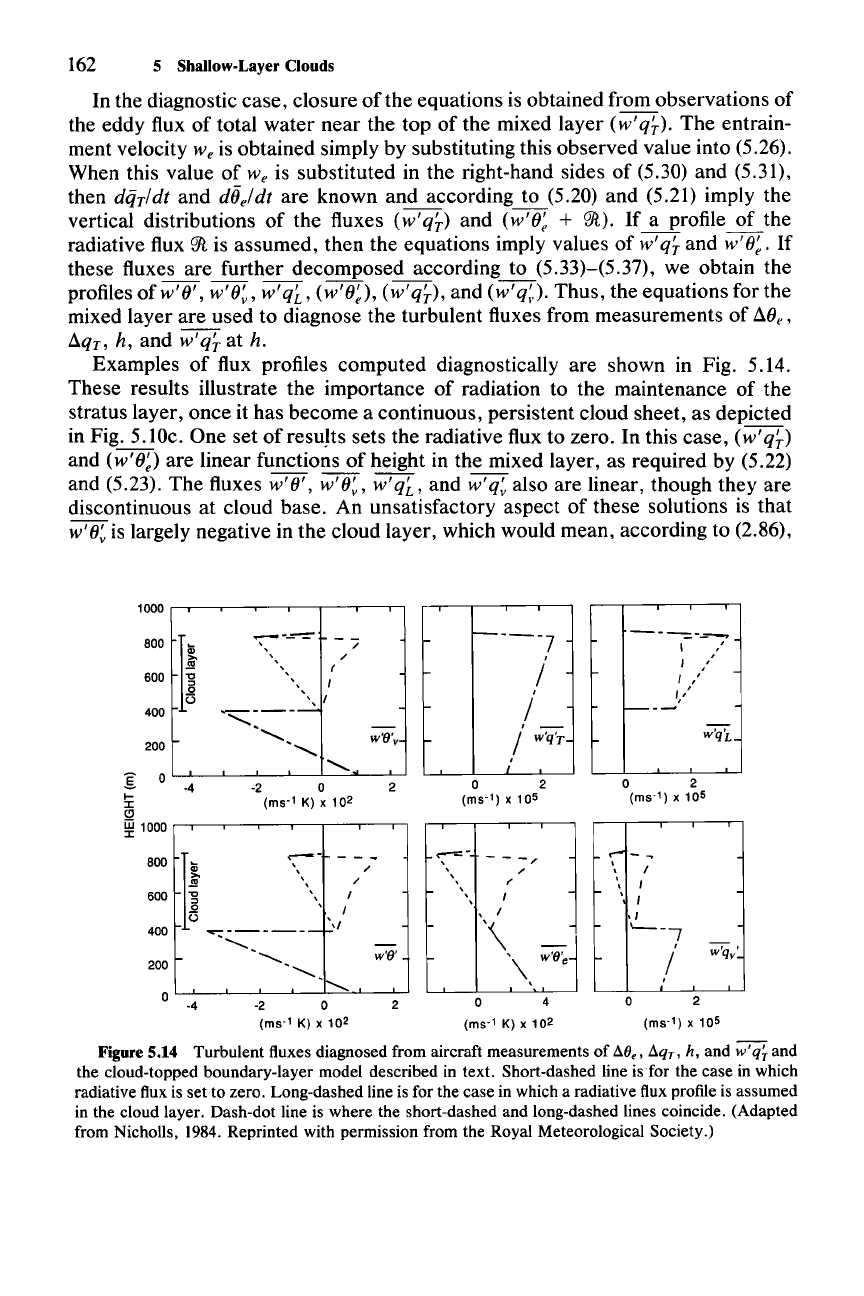
Examples of flux profiles computed diagnostically are shown in Fig. 5.14.

These results illustrate the importance of radiation to the maintenance of the

stratus layer, once it has become a continuous, persistent cloud sheet, as depicted

in Fig. 5.10c. One set of results sets the radiative flux to zero. In this case,

(w'q~)

and (w'O;) are linear functions of height in the mixed layer, as required by (5.22)

and (5.23). The fluxes

w'O',

w'O~,

q~,

and w'

also are linear, though they are

discontinuous at cloud base. An unsatisfactory aspect of these solutions is that

w'O~

is largely negative in the cloud layer, which would mean, according to (2.86),

----=--.

- "

J /

I :

_ ..

o 2

(ms'

)

x 10

o 2

(ms'

) x 10

;- -

, I

.. I

, I

'--,

I-

I w'q'T

1-----

o 4

(ms'

K) x 10

o 2

(ms'

)

x 10

·2 0

(ms·

x 10

~.~

-7

(

" ,

,---~

........................

w'O'v

200

w'O'

............

r-;

·4 ·2

(ms'

x 10

...---

800

600

-g

o '

(3 ,

400

~------

200

400

800

600

1000

I 0 .4

I-

:I:

1000

,,----.---,..---,-,----.----,--,

Figure 5.14 Turbulent fluxes diagnosed from aircraft measurements of

!!.()"

!!.qT, h, and w'

and

the cloud-topped boundary-layer model described in text. Short-dashed line is for the case in which

radiative flux is set to zero. Long-dashed line is for the case in which a radiative flux profile is assumed

in the cloud layer. Dash-dot line is where the short-dashed and long-dashed lines coincide. (Adapted

from Nicholls,

1984. Reprinted with permission from the Royal Meteorological Society.)

(5.39)

(5.40)

5.2 Stratus, Stratocumulus, and SmaU Cumulus in Boundary Layer Heated from Below

163

that turbulent kinetic energy is being destroyed in the cloud layer, thus contradict-

ing the characterization of the cloud as a turbulent entraining layer. When a

reasonable profile of upward radiative flux is assumed to apply in the cloud layer,

the results are modified as indicated in Fig. 5.14. In this case, the loss of heat by

radiation at cloud top is sufficiently large that the eddy flux of virtual potential

temperature (i.e., the buoyancy flux) can be positive throughout most of the cloud

layer. According to (2.86), the positive buoyancy flux generates turbulent kinetic

energy, and the stratus is consequently maintained as an active turbulent entrain-

ing cloud layer. Thus, after the cloud forms, the radiation in the cloud layer

becomes a crucial factor, continually destabilizing the lapse rate to maintain the

cloud as an unstable, turbulent layer.

In the prognostic application of the equations of the idealized mixed layer, one

cannot defer to observations to determine the entrainment velocity

We'

The ap-

proach generally used is to consider the budget of turbulent kinetic energy

'JC

in the

mixed layer, which is expressed by (2.86). In the boundary layer heated from

below and the cloud layer cooled at the top by radiation, buoyancy generation

(i};l

the important source term, while dissipation

q[; is the only sink of turbulent kinetic

energy in (2.86). Conversion from mean-flow kinetic energy

fi,

which also appears

in (2.86) may also contribute whenever the shear in the boundary layer is large,

but it is often not as significant as the buoyancy generation. In this regard, the

cloud-topped mixed layer is vastly different from the fog dynamics, considered in

Sec. 5.1, where buoyancy generation is zero or negative and all of the turbulence

must be derived from the weak mean flow. To keep our discussion as simple as

possible, we will consider the case where buoyancy generation is the only source

of turbulence. Generation via

and through pressure-velocity correlation

our

are

ignored. We also assume that

':J{

has no vertical or horizontal variability in the

well-mixed boundary layer. The total derivative

ott»

in (2.86) then simplifies to

d/dt.

With these assumptions, (2.86) becomes

d'JC

-=@-q[;

From (2.89), it is recalled that the buoyancy generation derives from the corre-

lation of buoyancy and vertical velocity. The vertical integral of the buoyancy

generation may be written as

(@;=

dz=

fg(W~~~)dZ

This integral has the units (velocity)", and

may be thought of as the portion of

the kinetic energy generation that is used to effect the entrainment. Various

schemes for determining what this portion should be have been devised, and this

remains a topic of research.

129

For

a review of some of these schemes, see Nicholls and Turton (1986).

(c)

(a)

(b)

20'

,::"

o ,

(c)

(a)

(b)

Figure 5.15

Figure 5.16

rows of

convergencel

divergence

(a)

(b) (c)

Figure 5.17

800 90° 60°

40° 20°

0°

-10° -60° 90°

600

-1.0

-0.8 -0.6 -0.4 -0.2 0 0.2 0.4

LATERAL

EKMAN

VELOCITY

0.6 0.8 1.0

Figure 5.18

5.2 Stratus, Stratocumulus, and Small Cumulus in Boundary Layer Heated from Below

165

5.2.3 Mesoscale Structure of Mixed-Layer Clouds

The layer of cloud at the top of the mixed layer often consists of discrete stratocu-

mulus elements in the form of rolls or cells. In this section, we will examine briefly

the factors giving rise to this structure, which we characterize as mesoscale since

the horizontal dimension of the cells and rolls ranges from 1 to 100 km. Not

everything about what leads to these patterns is known. However, there are three

processes that appear to play some role. These are the shear and thermal instabili-

ties

ofthe

boundary layer and the cloud-top entrainment process. These processes

will be considered in the sections below. We first consider long rolls of stratocu-

mulus, which are called

cloud streets.

5.2.3.1 Cloud Streets

In Sec. 2.9.2, it was shown that sheared flows are intrinsically unstable when

the Richardson number Ri

< 1/4 and that at the interface of two adjacent, horizon-

tally homogeneous, two-dimensional, inviscid, incompressible flows of different

density and velocity, this instability is manifest as Kelvin-Helmholtz waves (Figs.

2.6-2.8). These waves are the simplest form of a more general type of wave

motion, which can arise in sheared flows whenever the vertical profile of the wind

speed has an inflection point (i.e., a change of curvature).

130 Examples of two-

dimensional shear profiles that have been used in more sophisticated analyses of

Kelvin-Helmholtz instability are shown in Fig. 5.15. All of these profiles exhibit

Kelvin-Helmholtz waves, and each has an inflection point.

A wind profile with an inflection point can be produced by either speed shear or

by turning of the wind direction with height. The profiles in Fig. 5.16 are repre-

sented analytically by an arctangent profile in the vertical plane containing the tips

of the velocity vectors. These inflection point profiles are associated with pure

speed shear, speed plus turning, and pure turning. Stability analysis for convec-

130 The discussion of inflection point instability given here is based largely on comprehensive

review articles by Brown (1980, 1983).

Figure

5.15 Examples of two-dimensional shear profiles that have been used in analyses of

Kelvin-Helmholtz instability. Horizontal line divides fluid into two layers. Arrows indicate fluid

velocity. (From Brown, 1980.

Figure

5.16 Arctangent velocity variation between constant-velocity regions Va and V, over depth

h. (a) Pure speed shear. (b) Speed plus turning shear. (c) Pure turning shear. (From Brown, 1980.

Figure

5.17 Direction and orientation of phase lines of fastest-growing waves (and cloud streets)

with respect to type of velocity shear: (a) Pure speed shear. (b) Speed plus turning shear. (c) Pure

turning shear. (From Brown, 1980.

Figure

5.18 Theoretical Ekman-layer velocity profiles in perpendicular planes at various angles to

the free-stream (geostrophic) flow. The lateral Ekman velocity shown is the component of the

Ekman-layer wind perpendicular to planes oriented at various angles to the left of the geostrophic flow.

The velocity scale is labeled in fractions of the geostrophic wind speed. (From Brown, 1980.

American Geophysical Union.)

166 5 ShaUow-Layer Clouds

tively neutral conditions shows that all these profiles are unstable and that long

rolls are the preferred geometry of the most unstable solutions. The orientation of

the rolls depends on whether the profiles are due to speed shear or turning (Fig.

5.17). Pure speed shear leads to rolls perpendicular to the flow (Fig. 5.17a). These

are essentially Kelvin-Helmholtz billows. They have a characteristic wavelength

approximately twice the layer depth. Pure turning profiles (Fig. 5.17c) yield rolls

approximately parallel to the mean flow in the layer and have a characteristic

wavelength two to four times the layer depth.

is an interesting characteristic of the theoretical Ekman layer (Sec. 2.11.1)

that its velocity profile has an inflection point (Fig. 5.18). The inflection point

instability in the Ekman layer appears to produce disturbances which can grow to

finite size and come into equilibrium with the mean flow. The secondary roll flow

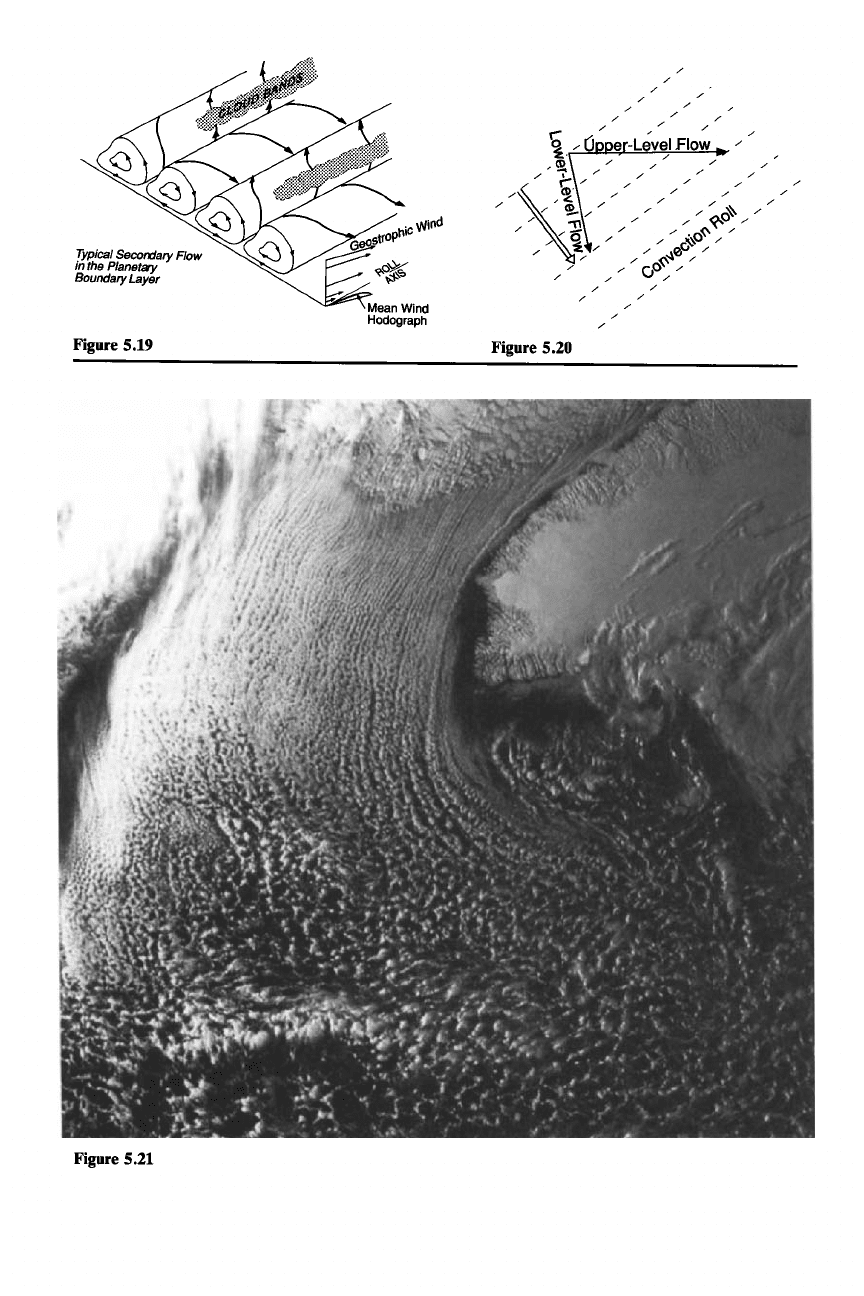
associated with an Ekman layer is illustrated in Fig. 5.19. The upward branches of

the rolls are conducive to supporting cloud lines generally parallel to mean flow in

the planetary boundary layerand may thus sometimes be responsible for organiza-

tion of stratocumulus, or small cumulus, into

cloud streets.

131

is doubtful that the inflection point shear instability alone accounts for cloud

streets. Usually there is also some degree of thermal instability in the planetary

boundary layer. When the boundary layer is heated from below, instability of the

Rayleigh-Benard type (Sec. 2.9.3) may arise. According to the instability crite-

rion (2.180), there is no preferred geometry of the convection in a stagnant basic

state. The convective overturning may be in the form of long rolls or symmetric

cells. However, the situation changes if the basic state of the unstable layer of

fluid is characterized by a horizontal velocity that changes with height. The con-

vective solutions then have a preferred geometry.

132 Specifically, they are in the

form of rolls parallel to the shear vector (Fig. 5.20).

We have also seen that when the thermal stratification is neutral, inflection

point instability rolls transverse to the shear can appear. The general case of a

thermally unstable and unstably sheared fluid layer has been considered theoreti-

cally.!" When the basic-state wind field for a layer heated from below is pre-

scribed to be a theoretical Ekman layer, Rayleigh-Benard rolls parallel to the

131 Long rows of clouds sitting atop the boundary layer were dubbed

"cloud

streets"

by glider

pilots. Since the top of one of these cloud rows marks the top of an updraft, and the row extends

downwind, the cloud street encompasses the optimum combination of tail wind and updraft, which

allows a long glide to be achieved. In 1935, Dr. E. Steinhoff reported the first glider flight in cloud

streets. He left from Bayreuth in western Germany and finally landed in Brunn, Czechoslovakia, a

distance of over 500 km and exceeding the world record for that time. There he met three other glider

pilots, who had

just

accomplished the same feat. Cloud streets are described by Kuettner (1947, 1959,

1971). He noted in 1959 that although the glider pilots had become

"fond"

of cloud streets,

"the

priority of the discovery that the tedious circling technique in columnar thermals could be replaced by

a comfortable tailwind flight beneath the cloud streets must be given to the seagulls

...

who seem to

have enjoyed this technique for millions of

years."

The observations of seagulls soaring was reported

by Woodcock (1942).

132 This effect was first noted when Benard tilted his cells in the laboratory.

133 An especially lucid account can be found in the series of articles of Asai (1964, 1970a,b, 1972)

and Asai and Nakasuji (1973).

5.2 Stratus, Stratocumulus, and Small Cumulus in Boundary Layer Heated from Below 167

shear dominate as long as the Richardson number is low (i.e., the differential

heating of the layer dominates). At higher Richardson number, inflection point

instability dominates, with rolls 20° to the left of the geostrophic flow. A "parallel

instability" mode, not associated with the inflection point, is also found.

characterized by rolls

10°

to the right of the geostrophic flow. However, the

parallel instability occurs under conditions not likely to be significant in the atmo-

sphere.P'

When cold air flows off a cold land mass or region of ice over an adjacent region

of warm water, well-defined cloud streets appear (Fig. 5.21; see also Figs. l.11b

and 1.30). In this situation, the shear and mean flow vectors in the boundary layer

are approximately the same; therefore, it is not easy to distinguish from the

orientation of the cloud streets whether they are of thermal or shear origin. How-

ever, the strong surface flux that occurs when the cold air lies over the warm

water indicates that the Richardson number is quite low and that the rolls are most

likely of the thermal instability type. Before the air reaches the water, inflection

point instability must dominate, and it probably produces rolls in the boundary

layer of size and orientation similar to the thermally induced rolls, but without the

cloud tracers to make their appearance evident in the satellite picture. When the

winds are moderate

(>5

S-2)

and the stratification is only weakly unstable, the

organization of the cloud streets is more likely dominated by the Ekman-layer

inflection point instability.

135

Returning to Fig. 5.21, we note that as the air flows farther out to sea, the cloud

rolls widen and deepen. Finally the cloud field turns into a more complex pattern

of clouds, which have more the character of cumulus or small cumulonimbus than

stratocumulus (as in Fig. 5.11b). The widening and deepening of the roll circula-

tions are not well understood. The roll circulations may grow as a result ofinstabil-

ity of the flow to perturbations of finite size. To the extent that cumulonimbus

occurs, precipitation may also affect the structure of the cloud pattern at this

stage.

Whatever the nature

ofthe

rolls, the upward branch of the roll circulation is the

favored environment for the formation of the cloud street. The flow is directed

along the rolls, and the stages of the life cycle of the cloud-topped mixed layer

depicted in Fig. 5.10 and Fig. 5.11 can be thought of as occurring at points along

the upward branch of a roll at locations successively farther out over the ocean,

while cloud formation is suppressed in the downward branches of the roIls. The

alternating cloud streets of stratocumulus and clear gaps comprise the cloud pat-

tern until far out to sea, where the stratocumulus elements develop into cumulus

or cumulonimbus and the pattern becomes more ceIlular.

5.2.3.2 Cellular Patterns

The cellular pattern seen out at sea in Fig. 5.21 is rather common for mixed-

layer clouds east of cold continents in the winter as well as offshore from large ice-

134 See Brown (1980) for discussion of the relative importance of the parallel and inflection point

modes.

iss LeMone (1973) has presented evidence to this effect.

Typical SeccrrJ

in the Planet

al)'

Flow

Boundal)'

La~r

Figure 5.19

Figure 5.21

MeanWind

Hodograph

Figure 5.20