Hirsch M., Smale S., Devaney R., Differential Equations, Dynamical Systems, and an Introduction to Chaos
Подождите немного. Документ загружается.


156 Chapter 7 Nonlinear Systems
record, use the value e = 2. 71828182845235360287 ... in calculat-
ing the error.
(h) Finally calculate how the error changes as you change the step size
from 0. 1 to 0. 05 and then from 0. 05 to 0. 01. That is, if ρ
denotes the
error made using step size , compute both ρ
0.1
/ρ
0.05
and ρ
0.05
/ρ
0.01
.
3. Now repeat the previous exploration, this time for the nonautonomous
equation x
= 2t (1 + x
2
). Use the value tan 1 = 1. 557407724654 ....
4. Discuss how the errors change as you shorten the step size by a factor of
2 or a factor of 5. Why, in particular, is the Runge-Kutta method called a
“fourth-order” method?
EXERCISES
1. Write out the first few terms of the Picard iteration scheme for each of the
following initial value problems. Where possible, find explicit solutions
and describe the domain of this solution.
(a) x
= x + 2; x(0) = 2
(b) x
= x
4/3
; x(0) = 0
(c) x
= x
4/3
; x(0) = 1
(d) x
= cos x; x(0) = 0
(e) x
= 1/(2x); x(1) = 1
2. Let A be an n × n matrix. Show that the Picard method for solving X
=
AX, X(0) = X
0
gives the solution exp(tA)X
0
.
3. Derive the Taylor series for sin 2t by applying the Picard method to the
first-order system corresponding to the second-order initial value problem
x
=−4x; x(0) = 0, x
(0) = 2.
4. Verify the linearity principle for linear, nonautonomous systems of
differential equations.
5. Consider the first-order equation x
= x/t. What can you say about
“solutions” that satisfy x(0) = 0? x(0) = a = 0?
6. Discuss the existence and uniqueness of solutions of the equation x
= x
a
where a>0 and x(0) = 0.
7. Let A(t ) be a continuous family of n×n matrices and let P(t ) be the matrix
solution to the initial value problem P
= A(t )P, P(0) = P
0
. Show that
det P(t ) = (det P
0
) exp
t
0
Tr A(s) ds
.
Exercises 157
8. Construct an example of a first-order differential equation on R for which
there are no solutions to any initial value problem.
9. Construct an example of a differential equation depending on a parameter
a for which some solutions do not depend continuously on a.
This Page Intentionally Left Blank

8
Equilibria in
Nonlinear Systems
To avoid some of the technicalities that we encountered in the previous chap-
ter, we henceforth assume that our differential equations are C
∞
, except when
specifically noted. This means that the right-hand side of the differential equa-
tion is k times continuously differentiable for all k. This will at the very least
allow us to keep the number of hypotheses in our theorems to a minimum.
As we have seen, it is often impossible to write down explicit solutions of
nonlinear systems of differential equations. The one exception to this occurs
when we have equilibrium solutions. Provided we can solve the algebraic
equations, we can write down the equilibria explicitly. Often, these are the
most important solutions of a particular nonlinear system. More importantly,
given our extended work on linear systems, we can usually use the technique of
linearization to determine the behavior of solutions near equilibrium points.
We describe this process in detail in this chapter.
8.1 Some Illustrative Examples
In this section we consider several planar nonlinear systems of differential
equations. Each will have an equilibrium point at the origin. Our goal is to see
that the solutions of the nonlinear system near the origin resemble those of
the linearized system, at least in certain cases.
159

160 Chapter 8 Equilibria in Nonlinear Systems
As a first example, consider the system:
x
= x + y
2
y
=−y.
There is a single equilibrium point at the origin. To picture nearby solutions,
we note that, when y is small, y
2
is much smaller. Hence, near the origin
at least, the differential equation x
= x + y
2
is very close to x
= x.In
Section 7.4 in Chapter 7 we showed that the flow of this system near the origin
is also “close” to that of the linearized system X
= DF
0
X. This suggests that
we consider instead the linearized equation
x
= x
y
=−y,
derived by simply dropping the higher order term. We can, of course, solve
this system immediately. We have a saddle at the origin with a stable line along
the y-axis and an unstable line along the x-axis.
Now let’s go back to the original nonlinear system. Luckily, we can also solve
this system explicitly. For the second equation y
=−y yields y(t) = y
0
e
−t
.
Inserting this into the first equation, we must solve
x
= x + y
2
0
e
−2t
.
This is a first-order, nonautonomous equation whose solutions may be deter-
mined as in calculus by “guessing” a particular solution of the form ce
−2t
.
Inserting this guess into the equation yields a particular solution:
x(t ) =−
1
3
y
2
0
e
−2t
.
Hence any function of the form
x(t ) = ce
t
−
1
3
y
2
0
e
−2t
is a solution of this equation, as is easily checked. The general solution is then
x(t ) =
x
0
+
1
3
y
2
0
e
t
−
1
3
y
2
0
e
−2t
y(t) = y
0
e
−t
.
If y
0
= 0, we find a straight-line solution x(t) = x
0
e
t
, y(t ) = 0, just as in
the linear case. However, unlike the linear case, the y-axis is no longer home

8.1 Some Illustrative Examples 161
Figure 8.1 The phase plane
for x
= x + y
2
, y
= −y.
Note the stable curve tangent
to the y-axis.
to a solution that tends to the origin. Indeed, the vector field along the y-axis is
given by (y
2
, −y), which is not tangent to the axis; rather, all nonzero vectors
point to the right along this axis.
On the other hand, there is a curve through the origin on which solutions
tend to (0, 0). Consider the curve x +
1
3
y
2
= 0inR
2
. Suppose (x
0
, y
0
) lies on
this curve, and let (x(t ), y(t )) be the solution satisfying this initial condition.
Since x
0
+
1
3
y
2
0
= 0 this solution becomes
x(t ) =−
1
3
y
2
0
e
−2t
y(t) = y
0
e
−t
.
Note that we have x(t ) +
1
3
(y(t))
2
= 0 for all t , so this solution remains
for all time on this curve. Moreover, as t →∞, this solution tends to the
equilibrium point. That is, we have found a stable curve through the origin on
which all solutions tend to (0, 0). Note that this curve is tangent to the y-axis
at the origin. See Figure 8.1.
Can we just “drop” the nonlinear terms in a system? The answer is, as we
shall see below, it depends! In this case, however, doing so is perfectly legal,
for we can find a change of variables that actually converts the original system
to the linear system.
To see this, we introduce new variables u and v via
u = x +
1
3
y
2
v = y.
162 Chapter 8 Equilibria in Nonlinear Systems
Then, in these new coordinates, the system becomes
u
= x
+
2
3
yy
= x +
1
3
y
2
= u
v
= y
=−y =−v.
That is to say, the nonlinear change of variables F (x, y) = (x +
1
3
y
2
, y) converts
the original nonlinear system to a linear one, in fact, to the linearized system
above.
Example. In general, it is impossible to convert a nonlinear system to a linear
one as in the previous example, since the nonlinear terms almost always make
huge changes in the system far from the equilibrium point at the origin. For
example, consider the nonlinear system
x
=
1
2
x − y −
1
2
x
3
+ y
2
x
y
= x +
1
2
y −
1
2
y
3
+ x
2
y
.
Again we have an equilibrium point at the origin. The linearized system is now
X
=
1
2
−1
1
1
2
X,
which has eigenvalues
1
2
± i. All solutions of this system spiral away from the
origin and toward ∞ in the counterclockwise direction, as is easily checked.
Solving the nonlinear system looks formidable. However, if we change to
polar coordinates, the equations become much simpler. We compute
r
cos θ − r(sin θ )θ
= x
=
1
2
r − r
3
cos θ − r sin θ
r
sin θ + r(cos θ )θ
= y
=
1
2
r − r
3
sin θ + r cos θ
from which we conclude, after equating the coefficients of cos θ and sin θ ,
r
= r(1 − r
2
)/2
θ
= 1.
We can now solve this system explicitly, since the equations are decoupled.
Rather than do this, we will proceed in a more geometric fashion. From the
equation θ
= 1, we conclude that all nonzero solutions spiral around the
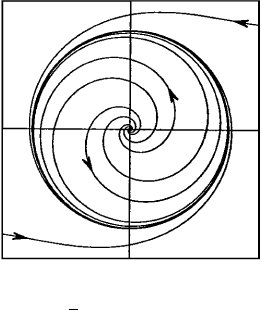
8.1 Some Illustrative Examples 163
Figure 8.2 The phase plane
for r
=
1
2
(r − r
3
), θ
=1.
origin in the counterclockwise direction. From the first equation, we see that
solutions do not spiral toward ∞. Indeed, we have r
= 0 when r = 1, so all
solutions that start on the unit circle stay there forever and move periodically
around the circle. Since r
> 0 when 0 <r<1, we conclude that nonzero
solutions inside the circle spiral away from the origin and toward the unit
circle. Since r
< 0 when r>1, solutions outside the circle spiral toward it.
See Figure 8.2.
In this example, there is no way to find a global change of coordinates that
puts the system into a linear form, since no linear system has this type of
spiraling toward a circle. However, near the origin this is still possible.
To see this, first note that if r
0
satisfies 0 <r
0
< 1, then the nonlinear vector
field points outside the circle of radius r
0
. This follows from the fact that, on
any such circle, r
= r
0
(1 − r
2
0
)/2 > 0. Consequently, in backward time, all
solutions of the nonlinear system tend to the origin, and in fact spiral as they
do so.
We can use this fact to define a conjugacy between the linear and nonlinear
system in the disk r ≤ r
0
, much as we did in Chapter 4. Let φ
t
denote the
flow of the nonlinear system. In polar coordinates, the linearized system above
becomes
r
= r/2
θ
= 1.
Let ψ
t
denote the flow of this system. Again, all solutions of the linear
system tend toward the origin in backward time. We will now define a
conjugacy between these two flows in the disk D given by r<1. Fix r
0
with 0 <r
0
< 1. For any point (r, θ )inD with r>0, there is a unique
164 Chapter 8 Equilibria in Nonlinear Systems
t = t (r, θ) for which φ
t
(r, θ ) belongs to the circle r = r
0
. We then define the
function
h(r, θ) = ψ
−t
φ
t
(r, θ )
where t = t (r, θ). We stipulate also that h takes the origin to the origin. Then
it is straightforward to check that
h ◦ φ
s
(r, θ ) = ψ
s
◦ h(r, θ)
for any point (r, θ)inD, so that h gives a conjugacy between the nonlinear
and linear systems. It is also easy to check that h takes D onto all of
R
2
.
Thus we see that, while it may not always be possible to linearize a system
globally, we may sometimes accomplish this locally. Unfortunately, such a
local linearization may not provide any useful information about the behavior
of solutions.
Example. Now consider the system
x
=−y + x(x
2
+ y
2
)
y
= x + y(x
2
+ y
2
).
Here is a parameter that we may take to be either positive or negative.
The linearized system is
x
=−y
y
= x,
so we see that the origin is a center and all solutions travel in the counter-
clockwise direction around circles centered at the origin with unit angular
speed.
This is hardly the case for the nonlinear system. In polar coordinates, this
system reduces to
r
= r
3
θ
=−1.
Thus when > 0, all solutions spiral away from the origin, whereas when
< 0, all solutions spiral toward the origin. The addition of the nonlinear
terms, no matter how small near the origin, changes the linearized phase
portrait dramatically; we cannot use linearization to determine the behavior
of this system near the equilibrium point.

8.2 Nonlinear Sinks and Sources 165
Figure 8.3 The phase plane
for x
= x
2
, y
= −y.
Example. Now consider one final example:
x
= x
2
y
=−y.
The only equilibrium solution for this system is the origin. All other solutions
(except those on the y-axis) move to the right and toward the x-axis. On the
y-axis, solutions tend along this straight line to the origin. Hence the phase
portrait is as shown in Figure 8.3.
Note that the picture in Figure 8.3 is quite different from the corresponding
picture for the linearized system
x
= 0
y
=−y,
for which all points on the x-axis are equilibrium points, and all other solutions
lie on vertical lines x = constant.
The problem here, as in the previous example, is that the equilibrium point
for the linearized system at the origin is not hyperbolic. When a linear planar
system has a zero eigenvalue or a center, the addition of nonlinear terms often
completely changes the phase portrait.
8.2 Nonlinear Sinks and Sources
As we saw in the examples of the previous section, solutions of planar nonlinear
systems near equilibrium points resemble those of their linear parts only in
