Hirsch M., Smale S., Devaney R., Differential Equations, Dynamical Systems, and an Introduction to Chaos

Подождите немного. Документ загружается.

136 Chapter 6 Higher Dimensional Linear Systems

2. Consider the linear system



⎛

⎝

0 λ

00λ

⎞

⎠

where λ

< λ

< 0. Describe how the solution through an arbitrary

initial value tends to the origin.

3. Give an example of a 3 × 3 matrix A for which all nonequilibrium

solutions of X



= AX are periodic with period 2π. Sketch the phase

portrait.

4. Find the general solution of



⎛

⎜

⎝

0110

−1001

0001

00−10

⎞

⎟

⎠

5. Consider the system



⎛

⎝

00a

0 b 0

a 00

⎞

⎠

depending on the two parameters a and b.

(a) Find the general solution of this system.

(b) Sketch the region in the ab–plane where this system has different

types of phase portraits.

6. Consider the system



⎛

⎝

a 0 b

0 b 0

−b 0 a

⎞

⎠

depending on the two parameters a and b.

(a) Find the general solution of this system.

(b) Sketch the region in the ab–plane where this system has different

types of phase portraits.

7. Coupled Harmonic Oscillators. In this series of exercises you are asked

to generalize the material on harmonic oscillators in Section 6.2 to the

case where the oscillators are coupled. Suppose there are two masses m

Exercises 137

Figure 6.10 A coupled oscillator.

and m

attached to springs and walls as shown in Figure 6.10. The springs

connecting m

to the walls both have spring constants k

, while the spring

connecting m

and m

has spring constant k

. This coupling means that

the motion of either mass affects the behavior of the other.

Let x

denote the displacement of each mass from its rest position, and

assume that both masses are equal to 1. The differential equations for

these coupled oscillators are then given by



=−(k

+ k



= k

− (k

+ k

These equations are derived as follows. If m

is moved to the right

> 0), the left spring is stretched and exerts a restorative force on

given by −k

. Meanwhile, the central spring is compressed, so it

exerts a restorative force on m

given by −k

. If the right spring is

stretched, then the central spring is compressed and exerts a restorative

force on m

given by k

(since x

< 0). The forces on m

are similar.

(a) Write these equations as a ﬁrst-order linear system.

(b) Determine the eigenvalues and eigenvectors of the corresponding

matrix.

(d) Let ω

√

and ω

√

+ 2k

. What can be said about the

periodicity of solutions relative to the ω

? Prove this.

8. Suppose X



= AX where A isa4×4 matrix whose eigenvalues are ±i

√

and ±i

√

3. Describe this ﬂow.

9. Suppose X



= AX where A isa4× 4 matrix whose eigenvalues are ±i

and −1 ± i. Describe this ﬂow.

10. Suppose X



= AX where A isa4× 4 matrix whose eigenvalues are ±i

and ±1. Describe this ﬂow.

11. Consider the system X



= AX where X = (x

, ..., x

) and

A =

⎛

⎜

⎝

0 ω

−ω

0 ω

−ω

−1

⎞

⎟

⎠

138 Chapter 6 Higher Dimensional Linear Systems

and ω

/ω

is irrational. Describe qualitatively how a solution behaves

when, at time 0, each x

is nonzero with the exception that

(a) x

= 0;

(b) x

= 0;

= x

= 0;

(d) x

= x

= 0.

12. Compute the exponentials of the following matrices:

(a)



5 −6

3 −4



(b)



2 −1



(c)



2 −1



(d)





(e)

⎛

⎝

012

003

000

⎞

⎠

(f )

⎛

⎝

200

030

013

⎞

⎠

(g)

⎛

⎝

λ 00

1 λ 0

01λ

⎞

⎠

(h)



i 0

0 −i



(i)



1 + i 0

21+ i



(j)

⎛

⎜

⎝

1000

⎞

⎟

⎠

13. Find an example of two matrices A, B such that

exp(A + B) = exp(

A) exp(B).

14. Show that if AB = BA, then

(a) exp(A) exp(B) = exp(B) exp(A)

(b) exp(A)B = B exp(A).

15. Consider the triplet of harmonic oscillators



=−x



=−2x



=−ω

where ω is irrational. What can you say about the qualitative behavior of

solutions of this six-dimensional system?

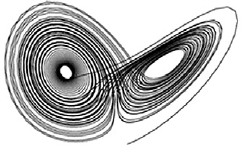
Nonlinear Systems

In this chapter we begin the study of nonlinear differential equations. Unlike

linear (constant coefﬁcient) systems, where we can always ﬁnd the explicit

solution of any initial value problem, this is rarely the case for nonlinear sys-

tems. In fact, basic properties such as the existence and uniqueness of solutions,

which was so obvious in the linear case, no longer hold for nonlinear systems.

As we shall see, some nonlinear systems have no solutions whatsoever to a

given initial value problem. On the other hand, some systems have inﬁnitely

many different such solutions. Even if we do ﬁnd a solution of such a sys-

tem, this solution need not be deﬁned for all time; for example, the solution

may tend to ∞ in ﬁnite time. And other questions arise: For example, what

happens if we vary the initial condition of a system ever so slightly? Does the

corresponding solution vary continuously? All of this is clear for linear sys-

tems, but not at all clear in the nonlinear case. This means that the underlying

theory behind nonlinear systems of differential equations is quite a bit more

complicated than that for linear systems.

In practice, most nonlinear systems that arise are “nice” in the sense that we

do have existence and uniqueness of solutions as well as continuity of solutions

when initial conditions are varied, and other “natural” properties. Thus we

have a choice: Given a nonlinear system, we could simply plunge ahead and

either hope that or, if possible, verify that, in each speciﬁc case, the system’s

solutions behave nicely. Alternatively, we could take a long pause at this stage

to develop the necessary hypotheses that guarantee that solutions of a given

nonlinear system behave nicely.

139

140 Chapter 7 Nonlinear Systems

In this book we pursue a compromise route. In this chapter, we will spell

out in precise detail many of the theoretical results that govern the behavior

of solutions of differential equations. We will present examples of how and

when these results fail, but we will not prove these theorems here. Rather,

we will postpone all of the technicalities until Chapter 17, primarily because

understanding this material demands a ﬁrm and extensive background in the

principles of real analysis. In subsequent chapters, we will make use of the

results stated here, but readers who are primarily interested in applications of

differential equations or in understanding how speciﬁc nonlinear systems may

be analyzed need not get bogged down in these details here. Readers who want

the technical details may take a detour to Chapter 17 now.

7.1 Dynamical Systems

As mentioned previously, most nonlinear systems of differential equations are

impossible to solve analytically. One reason for this is the unfortunate fact

that we simply do not have enough functions with speciﬁc names that we

can use to write down explicit solutions of these systems. Equally problem-

atic is the fact that, as we shall see, higher dimensional systems may exhibit

chaotic behavior, a property that makes knowing a particular explicit solution

essentially worthless in the larger scheme of understanding the behavior of the

system. Hence we are forced to resort to different means in order to understand

these systems. These are the techniques that arise in the ﬁeld of dynamical

systems. We will use a combination of analytic, geometric, and topological

techniques to derive rigorous results about the behavior of solutions of these

equations.

We begin by collecting some of the terminology regarding dynamical sys-

tems that we have introduced at various points in the preceding chapters. A

dynamical system is a way of describing the passage in time of all points of a

given space

S. The space S could be thought of, for example, as the space of

states of some physical system. Mathematically,

S might be a Euclidean space

or an open subset of Euclidean space or some other space such as a surface in

. When we consider dynamical systems that arise in mechanics, the space S

will be the set of possible positions and velocities of the system. For the sake of

simplicity, we will assume throughout that the space

S is Euclidean space R

although in certain cases the important dynamical behavior will be conﬁned

to a particular subset of

Given an initial position X ∈

, a dynamical system on R

tells us where

X is located 1 unit of time later, 2 units of time later, and so on. We denote

these new positions of X by X

, X

, and so forth. At time zero, X is located

at position X

. One unit before time zero, X was at X

−1

. In general, the

7.1 Dynamical Systems 141

“trajectory” of X is given by X

. If we measure the positions X

using only

integer time values, we have an example of a discrete dynamical system, which

we shall study in Chapter 15. If time is measured continuously with t ∈

we have a continuous dynamical system. If the system depends on time in

a continuously differentiable manner, we have a smooth dynamical system.

These are the three principal types of dynamical systems that arise in the

study of systems of differential equations, and they will form the backbone of

Chapters 8 through 14.

The function that takes t to X

yields either a sequence of points or a curve

that represents the life history of X as time runs from −∞ to ∞.

Different branches of dynamical systems make different assumptions about

how the function X

depends on t . For example, ergodic theory deals with

such functions under the assumption that they preserve a measure on

Topological dynamics deals with such functions under the assumption that

varies only continuously. In the case of differential equations, we will

usually assume that the function X

is continuously differentiable. The map

: R

→ R

that takes X into X

is deﬁned for each t and, from our

interpretation of X

as a state moving in time, it is reasonable to expect φ

have φ

−t

as its inverse. Also, φ

should be the identity function φ

(X) = X

and φ

(φ

(X)) = φ

t+s

(X) is also a natural condition. We formalize all of this

in the following deﬁnition:

Definition

A smooth dynamical system on

is a continuously differentiable

function φ :

R × R

→ R

where φ(t , X ) = φ

(X) satisfies

1. φ

: R

→ R

is the identity function: φ

) = X

;

2. The composition φ

◦ φ

= φ

t+s

for each t , s ∈ R.

Recall that a function is continuously differentiable if all of its partial deriva-

tives exist and are continuous throughout its domain. It is traditional to call a

continuously differentiable function a C

function. If the function is k times

continuously differentiable, it is called a C

function. Note that the deﬁnition

above implies that the map φ

: R

→ R

is C

for each t and has a C

inverse

−t

(take s =−t in part 2).

Example. For the ﬁrst-order differential equation x



= ax, the function

) = x

exp(at) gives the solutions of this equation and also deﬁnes a

smooth dynamical system on

R. 

Example. Let A be an n ×n matrix. Then the function φ

) = exp(tA)X

deﬁnes a smooth dynamical system on R

. Clearly, φ

= exp(0) = I and, as

142 Chapter 7 Nonlinear Systems

we saw in the previous chapter, we have

t+s

= exp((t + s)A) = (exp(tA))(exp(sA)) = φ

◦ φ



Note that these examples are intimately related to the system of differential

equations X



= AX . In general, a smooth dynamical system always yields a

vector ﬁeld on

via the following rule: Given φ

, let

F(X ) =



t=0

(X).

Then φ

is just the time t map associated to the ﬂow of X



= F(X).

Conversely, the differential equation X



= F(X) generates a smooth dynam-

ical system provided the time t map of the ﬂow is well deﬁned and continuously

differentiable for all time. Unfortunately, this is not always the case.

7.2 The Existence and Uniqueness

Theorem

We turn now to the fundamental theorem of differential equations, the

existence and uniqueness theorem. Consider the system of differential

equations



= F(X)

where F :

→ R

. Recall that a solution of this system is a function X : J →

deﬁned on some interval J ⊂ R such that, for all t ∈ J ,



(t) = F(X (t )).

Geometrically, X(t ) is a curve in

whose tangent vector X



(t) exists for all

t ∈ J and equals F(X(t )). As in previous chapters, we think of this vector

as being based at X (t), so that the map F :

→ R

deﬁnes a vector ﬁeld

.Aninitial condition or initial value for a solution X : J → R

a speciﬁcation of the form X(t

) = X

where t

∈ J and X

∈ R

. For

simplicity, we usually take t

= 0. The main problem in differential equations

is to ﬁnd the solution of any initial value problem; that is, to determine the

solution of the system that satisﬁes the initial condition X (0) = X

for each

∈ R

Unfortunately, nonlinear differential equations may have no solutions

satisfying certain initial conditions.

7.2 The Existence and Uniqueness Theorem 143

Example. Consider the simple ﬁrst-order differential equation





1ifx<0

−1ifx ≥ 0.

This vector ﬁeld on

R points to the left when x ≥ 0 and to the right if x<0.

Consequently, there is no solution that satisﬁes the initial condition x(0) = 0.

Indeed, such a solution must initially decrease since x



(0) =−1, but for all

negative values of x, solutions must increase. This cannot happen. Note further

that solutions are never deﬁned for all time. For example, if x

> 0, then the

solution through x

is given by x(t) = x

− t , but this solution is only valid

for −∞ <t<x

for the same reason as above.

The problem in this example is that the vector ﬁeld is not continuous at

0; whenever a vector ﬁeld is discontinuous we face the possibility that nearby

vectors may point in “opposing” directions, thereby causing solutions to halt

at these bad points.



Beyond the problem of existence of solutions of nonlinear differential equa-

tions, we also must confront the fact that certain equations may have many

different solutions to the same initial value problem.

Example. Consider the differential equation



= 3x

2/3

The identically zero function u :

R → R given by u(t ) ≡ 0 is clearly a solution

with initial condition u(0) = 0. But u

(t) = t

is also a solution satisfying this

initial condition. Moreover, for any τ > 0, the function given by

(t) =



0ift ≤ τ

(t − τ )

if t>τ

is also a solution satisfying the initial condition u

(0) = 0. While the differ-

ential equation in this example is continuous at x

= 0, the problems arise

because 3x

2/3

is not differentiable at this point. 

From these two examples it is clear that, to ensure existence and uniqueness

of solutions, certain conditions must be imposed on the function F. In the ﬁrst

example, F was not continuous at the problematic point 0, while in the second

example, F failed to be differentiable at 0. It turns out that the assumption that

F is continuously differentiable is sufﬁcient to guarantee both existence and

uniqueness of solutions, as we shall see. Fortunately, differential equations

that are not continuously differentiable rarely arise in applications, so the

144 Chapter 7 Nonlinear Systems

phenomenon of nonexistence or nonuniqueness of solutions with given initial

conditions is quite exceptional.

The following is the fundamental local theorem of ordinary differential

equations.

The Existence and Uniqueness Theorem. Consider the initial value

problem



= F(X), X(t

) = X

where X

∈ R

. Suppose that F : R

→ R

is C

. Then, ﬁrst of all, there exists a

solution of this initial value problem and, secondly, this is the only such solution.

More precisely, there exists an a > 0 and a unique solution

X : (t

− a, t

+ a) → R

of this differential equation satisfying the initial condition X (t

) = X

. 

The important proof of this theorem is contained in Chapter 17.

Without dwelling on the details here, the proof of this theorem depends

on an important technique known as Picard iteration. Before moving on, we

illustrate how the Picard iteration scheme used in the proof of the theorem

works in several special examples. The basic idea behind this iterative process

is to construct a sequence of functions that converges to the solution of the

differential equation. The sequence of functions u

(t) is deﬁned inductively

by u

(t) = x

where x

is the given initial condition, and then

r+1

(t) = x



(s) ds.

Example. Consider the simple differential equation x



= x. We will pro-

duce the solution of this equation satisfying x(0) = x

. We know, of course,

that this solution is given by x(t ) = x

. We will construct a sequence of

functions u

(t), one for each k, which converges to the actual solution x(t )as

k →∞.

We start with

(t) = x

the given initial value. Then we set

(t) = x



(s) ds = x



ds,

7.2 The Existence and Uniqueness Theorem 145

so that u

(t) = x

+ tx

. Given u

we deﬁne

(t) = x



(s) ds = x



+ sx

) ds,

so that u

(t) = x

+ tx

. You can probably see where this is heading.

Inductively, we set

k+1

(t) = x



(s) ds,

and so

k+1

(t) = x

k+1



i=0

As k →∞, u

(t) converges to

∞



i=0

= x

= x(t ),

which is the solution of our original equation.



Example. For an example of Picard iteration applied to a system of

differential equations, consider the linear system



= F(X) =



−10



with initial condition X (0) = (1, 0). As we have seen, the solution of this initial

value problem is

X(t ) =



cos t

−sin t



Using Picard iteration, we have

(t) =





(t) =











ds =









−1



ds =



−t



(t) =









−s

−1



ds =



1 − t

−t

