Hirsch M., Smale S., Devaney R., Differential Equations, Dynamical Systems, and an Introduction to Chaos

Подождите немного. Документ загружается.

146 Chapter 7 Nonlinear Systems

(t) =









−s

−1 + s



ds =



1 − t

−t + t

/3!



(t) =



1 − t

/2 + t

/4!

−t + t

/3!



and we see the inﬁnite series for the cosine and sine functions emerging from

this iteration.



Now suppose that we have two solutions Y (t ) and Z (t) of the differential

equation X



= F(X), and that Y (t) and Z(t) satisfy Y (t

) = Z(t

). Suppose

that both solutions are deﬁned on an interval J . The existence and uniqueness

theorem guarantees that Y (t ) = Z (t ) for all t in an interval about t

, which

may a priori be smaller than J . However, this is not the case. To see this,

suppose that J

∗

is the largest interval on which Y (t) = Z(t ). Let t

be an

endpoint of J

∗

. By continuity, we have Y (t

) = Z (t

). The theorem then

guarantees that, in fact, Y (t ) and Z (t ) agree on an open interval containing t

This contradicts the assertion that J

∗

is the largest interval on which the two

solutions agree.

Thus we can always assume that we have a unique solution deﬁned on a

maximal time domain. There is, however, no guarantee that a solution X(t )

can be deﬁned for all time, no matter how “nice” F(X) is.

Example. Consider the differential equation in

R given by



= 1 + x

This equation has as solutions the functions x(t ) = tan(t + c) where c is a

constant. Such a function cannot be extended over an interval larger than

−c −

<t<−c +

since x(t ) →±∞as t →−c ± π /2.



This example is typical, for we have

Theorem. Let U ⊂

be an open set, and let F : U → R

be C

. Let X(t)

be a solution of X



= F(X) deﬁned on a maximal open interval J = (α, β) ⊂ R

with β < ∞. Then given any closed and bounded set K ⊂ U , there is some

t ∈ (α, β) with X(t) ∈ K.



This theorem says that if a solution X(t) cannot be extended to a larger time

interval, then this solution leaves any closed and bounded set in U . This implies

7.3 Continuous Dependence of Solutions 147

that X (t ) must come arbitrarily close to the boundary of U as t → β. Similar

results hold as t → α.

7.3 Continuous Dependence of Solutions

For the existence and uniqueness theorem to be at all interesting in any physical

(or even mathematical) sense, this result needs to be complemented by the

property that the solution X (t) depends continuously on the initial condition

X(0). The next theorem gives a precise statement of this property.

Theorem. Consider the differential equation X



= F(X) where F : R

→ R

is C

. Suppose that X (t ) is a solution of this equation which is deﬁned on the

closed interval [t

, t

] with X(t

) = X

. Then there is a neighborhood U ⊂ R

of X

and a constant K such that if Y

∈ U , then there is a unique solution Y (t )

also deﬁned on [t

, t

] with Y (t

) = Y

. Moreover Y (t ) satisﬁes

|Y (t ) − X(t)|≤K |Y

− X

|exp(K (t − t

))

for all t ∈[t

, t

]. 

This result says that, if the solutions X(t ) and Y (t ) start out close together,

then they remain close together for t close to t

. While these solutions may

separate from each other, they do so no faster than exponentially. In particular,

since the right-hand side of this inequality depends on |Y

− X

|, which we

may assume is small, we have:

Corollary. (Continuous Dependence on Initial Conditions) Let

φ(t , X) be the ﬂow of the system X



= F (X) where F is C

. Then φ is a

continuous function of X .



Example. Let k>0. For the system





−10

0 k



we know that the solution X(t) satisfying X (0) = (−1, 0) is given by

X(t ) = (−e

−t

, 0).

For any η = 0, let Y

(t) be the solution satisfying Y

(0) = (−1, η). Then

(t) = (−e

−t

, ηe

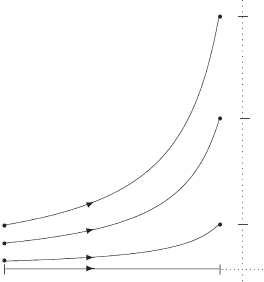
148 Chapter 7 Nonlinear Systems

X(t)

⫺1

(⫺1, g

)

(t)

⫺e

⫺r

Figure 7.1 The solutions Y

(t) separate

exponentially from X (t) but nonetheless

are continuous in their initial conditions.

As in the theorem, we have

(t) − X(t )|=|ηe

− 0|=|η − 0|e

=|Y

(0) − X(0)|e

The solutions Y

do indeed separate from X (t ), as we see in Figure 7.1, but

they do so at most exponentially. Moreover, for any ﬁxed time t , we have

(t) → X(t)asη → 0. 

Differential equations often depend on parameters. For example, the har-

monic oscillator equations depend on the parameters b (the damping constant)

and k (the spring constant). Then the natural question is how do solutions of

these equations depend on these parameters? As in the previous case, solutions

depend continuously on these parameters provided that the system depends

on the parameters in a continuously differentiable fashion. We can see this

easily by using a special little trick. Suppose the system



= F

(X)

depends on the parameter a in a C

fashion. Let’s consider an “artiﬁcially”

augmented system of differential equations given by



= f

, ..., x

, a)



= f

, ..., x

, a)



= 0.

7.4 The Variational Equation 149

This is now an autonomous system of n +1 differential equations. While this

expansion of the system may seem trivial, we may now invoke the previous

result about continuous dependence of solutions on initial conditions to verify

that solutions of the original system depend continuously on a as well.

Theorem. (Continuous Dependence on Parameters) Let X



= F

(X)

be a system of differential equations for which F

is continuously differentiable

in both X and a. Then the ﬂow of this system depends continuously on a as

well.



7.4 The Variational Equation

Consider an autonomous system X



= F(X ) where, as usual, F is assumed to

be C

. The ﬂow φ(t , X ) of this system is a function of both t and X . From the

results of the previous section, we know that φ is continuous in the variable X .

We also know that φ is differentiable in the variable t , since t → φ(t , X ) is just

the solution curve through X. In fact, φ is also differentiable in the variable X,

for we shall prove in Chapter 17:

Theorem. (Smoothness of Flows). Consider the system X



= F(X) where

FisC

. Then the ﬂow φ(t , X) of this system is a C

function; that is, ∂φ/∂t and

∂φ/∂X exist and are continuous in t and X.



Note that we can compute ∂φ/∂t for any value of t as long as we know the

solution passing through X

, for we have

∂φ

∂t

(t, X

) = F(φ(t , X

)).

We also have

∂φ

∂X

(t, X

) = Dφ

)

where Dφ

is the Jacobian of the function X → φ

(X). To compute ∂φ/∂X,

however, it appears that we need to know the solution through X

as well as

the solutions through all nearby initial positions, since we need to compute

the partial derivatives of the various components of φ

. However, we can

get around this difﬁculty by introducing the variational equation along the

solution through X

To accomplish this, we need to take another brief detour into the world of

nonautonomous differential equations. Let A(t ) be a family of n ×n matrices

150 Chapter 7 Nonlinear Systems

that depends continuously on t . The system



= A(t )X

is a linear, nonautonomous system. We have an existence and uniqueness

theorem for these types of equations:

Theorem. Let A(t) be a continuous family of n × n matrices deﬁned for t ∈

[α, β]. Then the initial value problem



= A(t )X , X (t

) = X

has a unique solution that is deﬁned on the entire interval [α, β]. 

Note that there is some additional content to this theorem: We do not

assume that the right-hand side is a C

function in t . Continuity of A(t)

sufﬁces to guarantee existence and uniqueness of solutions.

Example. Consider the ﬁrst-order, linear, nonautonomous differential

equation



= a(t )x.

The unique solution of this equation satisfying x(0) = x

is given by

x(t ) = x

exp





a(s) ds



as is easily checked using the methods of Chapter 1. All we need is that a(t )is

continuous in order that x



(t) = a(t )x(t ); we do not need differentiability of

a(t ) for this to be true.



Note that solutions of linear, nonautonomous equations satisfy the linearity

principle. That is, if Y (t ) and Z (t ) are two solutions of such a system, then so

too is αY (t ) + βZ (t ) for any constants α and β.

Now we return to the autonomous, nonlinear system X



= F(X ). Let X(t )

be a particular solution of this system deﬁned for t in some interval J =[α, β].

Fix t

∈ J and set X(t

) = X

. For each t ∈ J let

A(t ) = DF

X(t)

where DF

X(t)

denotes the Jacobian matrix of F at the point X (t ) ∈ R

. Since

F is C

, A(t ) = DF

X(t)

is a continuous family of n ×n matrices. Consider the

7.4 The Variational Equation 151

nonautonomous linear equation



= A(t )U .

This equation is known as the variational equation along the solution X(t ). By

the previous theorem, we know that this variational equation has a solution

deﬁned on all of J for every initial condition U (t

) = U

The signiﬁcance of this equation is that, if U (t ) is the solution of the

variational equation that satisﬁes U (t

) = U

, then the function

t → X(t) + U (t )

is a good approximation to the solution Y (t ) of the autonomous equation

with initial value Y (t

) = X

+ U

, provided U

is sufﬁciently small. This is

the content of the following result.

Proposition. Consider the system X



= F(X) where F is C

. Suppose

1. X (t) is a solution of X



= F(X ), which is deﬁned for all t ∈[α, β] and

satisﬁes X (t

) = X

;

2. U (t) is the solution to the variational equation along X(t) that satisﬁes

U (t

) = U

;

3. Y (t ) is the solution of X



= F(X) that satisﬁes Y (t

) = X

+ U

Then

lim

→0

|Y (t ) − (X(t) + U (t ))|

converges to 0 uniformly in t ∈[α, β].



Technically, this means that for every  > 0 there exists δ > 0 such that if

|≤δ, then

|Y (t ) − (X(t) + U (t ))|≤|U

for all t ∈[α, β]. Thus, as U

→ 0, the curve t → X(t ) + U (t ) is a better

and better approximation to Y (t ). In many applications, the solution of the

variational equation X(t ) + U (t) is used in place of Y (t ); this is convenient

because U (t ) depends linearly on U

by the linearity principle.

Example. Consider the nonlinear system of equations



= x + y



=−y.

We will discuss this system in more detail in the next chapter. For now, note

that we know one solution of this system explicitly, namely, the equilibrium

152 Chapter 7 Nonlinear Systems

solution at the origin X (t ) ≡ (0, 0). The variational equation along this

solution is given by



= DF

(U ) =



0 −1



U ,

which is an autonomous linear system. We obtain the solutions of this equation

immediately: They are given by

U (t ) =



−t



The result above then guarantees that the solution of the nonlinear equation

through (x

, y

) and deﬁned on the interval [−τ , τ ] is as close as we wish to

U (t ), provided (x

, y

) is sufﬁciently close to the origin. 

Note that the arguments in this example are perfectly general. Given any

nonlinear system of differential equations X



= F(X) with an equilibrium

point at X

, we may consider the variational equation along this solution. But

is a constant matrix A. The variational equation is then U



= AU , which

is an autonomous linear system. This system is called the linearized system at

. We know that ﬂow of the linearized system is exp(tA)U

, so the result

above says that near an equilibrium point of a nonlinear system, the phase

portrait resembles that of the corresponding linearized system. We will make

the term resembles more precise in the next chapter.

Using the previous proposition, we may now compute ∂φ/∂X, assuming we

know the solution X (t ):

Theorem. Let X



= F(X ) be a system of differential equations where F is C

Let X (t ) be a solution of this system satisfying the initial condition X(0) = X

and deﬁned for t ∈[α, β], and let U (t , U

) be the solution to the variational

equation along X (t ) that satisﬁes U (0, U

) = U

. Then

Dφ

) U

= U (t, U

That is, ∂φ/∂X applied to U

is given by solving the corresponding variational

equation starting at U

Proof: Using the proposition, we have for all t ∈[α, β]:

Dφ

= lim

h→0

+ hU

) − φ

)

= lim

h→0

U (t , hU

)

= U (t, U



7.5 Exploration: Numerical Methods 153

Example. As an illustration of these ideas, consider the differential equation



= x

. An easy integration shows that the solution x(t ) satisfying the initial

condition x(0) = x

x(t ) =

−x

t − 1

Hence we have

∂φ

∂x

(t, x

) =

t − 1)

On the other hand, the variational equation for x(t )is



= 2x(t ) u =

−2x

t − 1

The solution of this equation satisfying the initial condition u(0) = u

given by

u(t ) = u



t − 1



as required. 

7.5 Exploration: Numerical Methods

In this exploration, we ﬁrst describe three different methods for approximating

the solutions of ﬁrst-order differential equations. Your task will be to evaluate

the effectiveness of each method.

Each of these methods involves an iterative process whereby we ﬁnd a

sequence of points (t

, x

) that approximates selected points (t

, x(t

)) along

the graph of a solution of the ﬁrst-order differential equation x



= f (t , x). In

each case we will begin with an initial value x(0) = x

.Sot

= 0 and x

is our

given initial value. We need to produce t

and x

In each of the three methods we will generate the t

recursively by choosing

a step size t and simply incrementing t

at each stage by t . Hence

k+1

= t

+ t

in each case. Choosing t small will (hopefully) improve the accuracy of the

method.

Therefore, to describe each method, we only need to determine the values

of x

. In each case, x

k+1

will be the x-coordinate of the point that sits directly

154 Chapter 7 Nonlinear Systems

over t

k+1

on a certain straight line through (t

, x

)inthetx–plane. Thus all we

need to do is to provide you with the slope of this straight line and then x

k+1

is determined. Each of the three methods involves a different straight line.

1. Euler’s method. Here x

k+1

is generated by moving t time units along

the straight line generated by the slope ﬁeld at the point (t

, x

). Since the

slope at this point is f (t

, x

), taking this short step puts us at

k+1

= x

+ f (t

, x

) t .

2. Improved Euler’s method. In this method, we use the average of two slopes

to move from (t

, x

)to(t

k+1

, x

k+1

). The ﬁrst slope is just that of the

slope ﬁeld at (t

, x

), namely,

= f (t

, x

The second is the slope of the slope ﬁeld at the point (t

k+1

, y

), where

is the terminal point determined by Euler’s method applied at (t

, x

That is,

= f (t

k+1

, y

) where y

= x

+ f (t

, x

) t .

Then we have

k+1

= x



+ n



t.

3. (Fourth-order) Runge-Kutta method. This method is the one most often

used to solve differential equations. There are more sophisticated numer-

ical methods that are speciﬁcally designed for special situations, but this

method has served as a general-purpose solver for decades. In this method,

we will determine four slopes, m

, n

, p

, and q

. The step from (t

, x

)

to (t

k+1

, x

k+1

) will be given by moving along a straight line whose slope

is a weighted average of these four values:

k+1

= x



+ 2n

+ 2p

+ q



t.

These slopes are determined as follows:

(a) m

is given as in Euler’s method:

= f (t

, x

7.5 Exploration: Numerical Methods 155

(b) n

is the slope at the point obtained by moving halfway along the

slope ﬁeld line at (t

, x

) to the intermediate point (t

+(t )/2, y

so that

= f (t

t

, y

) where y

= x

+ m

t

is the slope at the point obtained by moving halfway along a

different straight line at (t

, x

), where the slope is now n

rather

than m

as before. Hence

= f (t

t

, z

) where z

= x

+ n

t

(d) Finally, q

is the slope at the point (t

k+1

, w

) where we use a line with

slope p

at (t

, x

) to determine this point. Hence

= f (t

k+1

, w

) where w

= x

+ p

t.

Your goal in this exploration is to compare the effectiveness of these three

methods by evaluating the errors made in carrying out this procedure in sev-

eral examples. We suggest that you use a spreadsheet to make these lengthy

calculations.

1. First, just to make sure you comprehend the rather terse descriptions of

the three methods above, draw a picture in the tx–plane that illustrates

the process of moving from (t

, x

)to(t

k+1

, x

k+1

) in each of the three

cases.

2. Now let’s investigate how the various methods work when applied to an

especially simple differential equation, x



= x.

(a) First ﬁnd the explicit solution x(t ) of this equation satisfying the

initial condition x(0) = 1 (now there’s a free gift from the math

department...).

(b) Now use Euler’s method to approximate the value of x(1) = e using

the step size t = 0. 1. That is, recursively determine t

and x

for

k = 1, ..., 10 using t = 0. 1 and starting with t

= 0 and x

= 1.

(d) Again use Euler’s method, this time reducing the step size by a factor

of 5, so that t = 0. 01, to approximate x(1).

(e) Now repeat the previous three steps using the improved Euler’s

method with the same step sizes.

(f) And now repeat using Runge-Kutta.

(g) You now have nine different approximations for the value of x(1) =

e, three for each method. Now calculate the error in each case. For the