Hirsch M., Smale S., Devaney R., Differential Equations, Dynamical Systems, and an Introduction to Chaos
Подождите немного. Документ загружается.


176 Chapter 8 Equilibria in Nonlinear Systems
saw in Section 8.1. Even a small linear perturbation can make a center into a
sink or a source.
Thus when the linearization of the system at an equilibrium point is hyper-
bolic, we can immediately determine the stability of that point. Unfortunately,
many important equilibrium points that arise in applications are nonhyper-
bolic. It would be wonderful to have a technique that determined the stability
of an equilibrium point that works in all cases. Unfortunately, as yet, we have
no universal way of determining stability except by actually finding all solu-
tions of the system, which is usually difficult if not impossible. We will present
some techniques that allow us to determine stability in certain special cases in
the next chapter.
8.5 Bifurcations
In this section we will describe some simple examples of bifurcations that occur
for nonlinear systems. We consider a family of systems
X
= F
a
(X)
where a is a real parameter. We assume that F
a
depends on a in a C
∞
fashion.
A bifurcation occurs when there is a “significant” change in the structure of
the solutions of the system as a varies. The simplest types of bifurcations occur
when the number of equilibrium solutions changes as a varies.
Recall the elementary bifurcations we encountered in Chapter 1 for first-
order equations x
= f
a
(x). If x
0
is an equilibrium point, then we have f
a
(x
0
) =
0. If f
a
(x
0
) = 0, then small changes in a do not change the local structure near
x
0
: that is, the differential equation
x
= f
a+
(x)
has an equilibrium point x
0
() that varies continuously with for small.
A glance at the (increasing or decreasing) graphs of f
a+
(x) near x
0
shows
why this is true. More rigorously, this is an immediate consequence of the
implicit function theorem (see Exercise 3 at the end of this chapter). Thus
bifurcations for first-order equations only occur in the nonhyperbolic case
where f
a
(x
0
) = 0.
Example. The first-order equation
x
= f
a
(x) = x
2
+ a

8.5 Bifurcations 177
has a single equilibrium point at x = 0 when a = 0. Note f
0
(0) = 0, but
f
0
(0) = 0. For a>0 this equation has no equilibrium points since f
a
(x) > 0
for all x, but for a<0 this equation has a pair of equilibria. Thus a bifurcation
occurs as the parameter passes through a = 0.
This kind of bifurcation is called a saddle-node bifurcation (we will see the
“saddle” in this bifurcation a little later). In a saddle-node bifurcation, there is
an interval about the bifurcation value a
0
and another interval I on the x-axis
in which the differential equation has
1. Two equilibrium points in I if a<a
0
;
2. One equilibrium point in I if a = a
0
;
3. No equilibrium points in I if a>a
0
.
Of course, the bifurcation could take place “the other way,” with no equilibria
when a>a
0
. The example above is actually the typical type of bifurcation for
first-order equations.
Theorem. (Saddle-Node Bifurcation) Suppose x
= f
a
(x) is a first-order
differential equation for which
1. f
a
0
(x
0
) = 0;
2. f
a
0
(x
0
) = 0;
3. f
a
0
(x
0
) = 0;
4.
∂f
a
0
∂a
(x
0
) = 0.
Then this differential equation undergoes a saddle-node bifurcation at a = a
0
.
Proof: Let G(x, a) = f
a
(x). We have G(x
0
, a
0
) = 0. Also,
∂G
∂a
(x
0
, a
0
) =
∂f
a
0
∂a
(x
0
) = 0,
so we may apply the implicit function theorem to conclude that there is a
smooth function a = a(x) such that G(x, a(x)) = 0. In particular, if x
∗
belongs to the domain of a(x), then x
∗
is an equilibrium point for the equation
x
= f
a(x
∗
)
(x), since f
a(x
∗
)
(x
∗
) = 0. Differentiating G(x, a(x)) = 0 with
respect to x,wefind
a
(x) =
−∂G/∂x
∂G/∂a
.

178 Chapter 8 Equilibria in Nonlinear Systems
Now (∂G/∂x)(x
0
, a
0
) = f
a
0
(x
0
) = 0, while (∂G/∂a)(x
0
, a
0
) = 0 by assump-
tion. Hence a
(x
0
) = 0. Differentiating once more, we find
a
(x) =
−
∂
2
G
∂x
2
∂G
∂a
+
∂G
∂x
∂
2
G
∂a
2
∂G
∂a
2
.
Since (∂G/∂x)(x
0
, a
0
) = 0, we have
a
(x
0
) =
−
∂
2
G
∂x
2
(x
0
, a
0
)
∂G
∂a
(x
0
, a
0
)
= 0
since (∂
2
G/∂x
2
)(x
0
, a
0
) = f
a
0
(x
0
) = 0. This implies that the graph of a = a(x)
is either concave up or concave down, so we have two equilibria near x
0
for
a-values on one side of a
0
and no equilibria for a-values on the other side.
We said earlier that such saddle-node bifurcations were the “typical” bifur-
cations involving equilibrium points for first-order equations. The reason for
this is that we must have both
1. f
a
0
(x
0
) = 0
2. f
a
0
(x
0
) = 0
if x
= f
a
(x) is to undergo a bifurcation when a = a
0
. Generically (in the sense
of Section 5.6), the next higher order derivatives at (x
0
, a
0
) will be nonzero.
That is, we typically have
3. f
a
0
(x
0
) = 0
4.
∂f
a
∂a
(x
0
, a
0
) = 0
at such a bifurcation point. But these are precisely the conditions that guarantee
a saddle-node bifurcation.
Recall that the bifurcation diagram for x
= f
a
(x) is a plot of the various
phase lines of the equation versus the parameter a. The bifurcation diagram
for a typical saddle-node bifurcation is displayed in Figure 8.6. (The directions
of the arrows and the curve of equilibria may change.)
Example. (Pitchfork Bifurcation) Consider
x
= x
3
− ax.
8.5 Bifurcations 179
x
a
0
x
0
a
Figure 8.6 The bifurcation diagram for a
saddle-node bifurcation.
x
a
Figure 8.7 The bifurcation diagram
for a pitchfork bifurcation.
There are three equilibria for this equation, at x = 0 and x =±
√
a when
a>0. When a ≤ 0, x = 0 is the only equilibrium point. The bifurcation
diagram shown in Figure 8.7 explains why this bifurcation is so named.
Now we turn to some bifurcations in higher dimensions. The saddle-node
bifurcation in the plane is similar to its one-dimensional cousin, only now we
see where the “saddle” comes from.
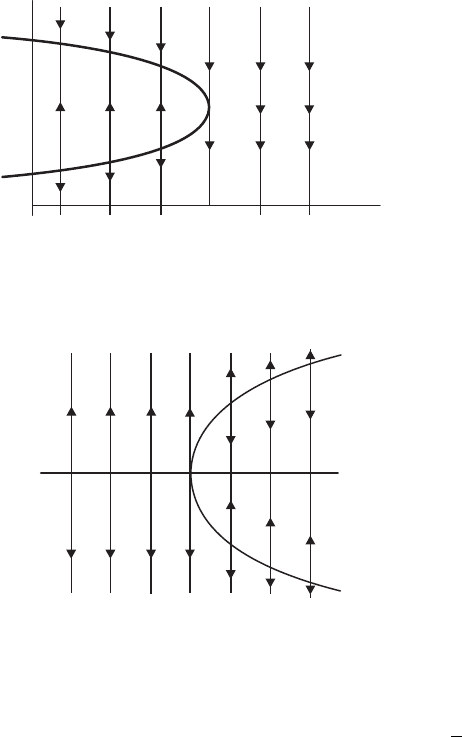
Example. Consider the system
x
= x
2
+ a
y
=−y.

180 Chapter 8 Equilibria in Nonlinear Systems
Figure 8.8 The saddle-node bifurcation when, from left to right,
a <0,a =0,anda >0.
When a = 0, this is one of the systems considered in Section 8.1. There is a
unique equilibrium point at the origin, and the linearized system has a zero
eigenvalue.
When a passes through a = 0, a saddle-node bifurcation occurs. When
a>0, we have x
> 0 so all solutions move to the right; the equilibrium point
disappears. When a<0 we have a pair of equilibria, at the points (±
√
−a, 0).
The linearized equation is
X
=
2x 0
0 −1
X.
So we have a sink at (−
√
−a, 0) and a saddle at (
√
−a, 0). Note that solutions
on the lines x =±
√
−a remain for all time on these lines since x
= 0 on these
lines. Solutions tend directly to the equilibria on these lines since y
=−y.
This bifurcation is sketched in Figure 8.8.
A saddle-node bifurcation may have serious global implications for the
behavior of solutions, as the following example shows.
Example. Consider the system given in polar coordinates by
r
= r − r
3
θ
= sin
2
(θ) + a
where a is again a parameter. The origin is always an equilibrium point since
r
= 0 when r = 0. There are no other equilibria when a>0 since, in that
case, θ
> 0. When a = 0 two additional equilibria appear at (r, θ) = (1, 0)
and (r, θ) = (1, π). When −1 <a<0, there are four equilibria on the circle
r = 1. These occur at the roots of the equation
sin
2
(θ) =−a.
8.5 Bifurcations 181
We denote these roots by θ
±
and θ
±
+π , where we assume that 0 < θ
+
< π /2
and −π /2 < θ
−
< 0.
Note that the flow of this system takes the straight rays through the origin
θ = constant to other straight rays. This occurs since θ
depends only on θ ,
not on r. Also, the unit circle is invariant in the sense that any solution that
starts on the circle remains there for all time. This follows since r
= 0 on this
circle. All other nonzero solutions tend to this circle, since r
> 0if0<r<1
whereas r
< 0ifr>1.
Now consider the case a = 0. In this case the x-axis is invariant and all
nonzero solutions on this line tend to the equilibrium points at x =±1. In
the upper half-plane we have θ
> 0, so all other solutions in this region wind
counterclockwise about 0 and tend to x =−1; the θ -coordinate increases
to θ = π while r tends monotonically to 1. No solution winds more than
angle π about the origin, since the x-axis acts as a barrier. The system behaves
symmetrically in the lower half-plane.
When a>0 two things happen. First of all, the equilibrium points at x =±1
disappear and now θ
> 0 everywhere. Thus the barrier on the x-axis has been
removed and all solutions suddenly are free to wind forever about the origin.
Secondly, we now have a periodic solution on the circle r = 1, and all nonzero
solutions are attracted to it.
This dramatic change is caused by a pair of saddle-node bifurcations at
a = 0. Indeed, when −1 <a<0 we have two pair of equilibria on the unit
circle. The rays θ = θ
±
and θ = θ
±
+ π are invariant, and all solutions
on these rays tend to the equilibria on the circle. Consider the half-plane
θ
−
< θ < θ
−
+ π. For θ-values in the interval θ
−
< θ < θ
+
, we have θ
< 0,
while θ
> 0 in the interval θ
+
< θ < θ
−
+π . Solutions behave symmetrically
in the complementary half-plane. Therefore all solutions that do not lie on the
rays θ = θ
+
or θ = θ
+
+ π tend to the equilibrium points at r = 1, θ = θ
−
or at r = 1, θ = θ
−
+ π. These equilibria are therefore sinks. At the other
equilibria we have saddles. The stable curves of these saddles lie on the rays
θ = θ
+
and θ = π + θ
+
and the unstable curves of the saddles are given by
the unit circle minus the sinks. See Figure 8.9.
The previous examples all featured bifurcations that occur when the lin-
earized system has a zero eigenvalue. Another case where the linearized system
fails to be hyperbolic occurs when the system has pure imaginary eigenvalues.
Example. (Hopf Bifurcation) Consider the system
x
= ax − y − x(x
2
+ y
2
)
y
= x + ay − y(x
2
+ y
2
).
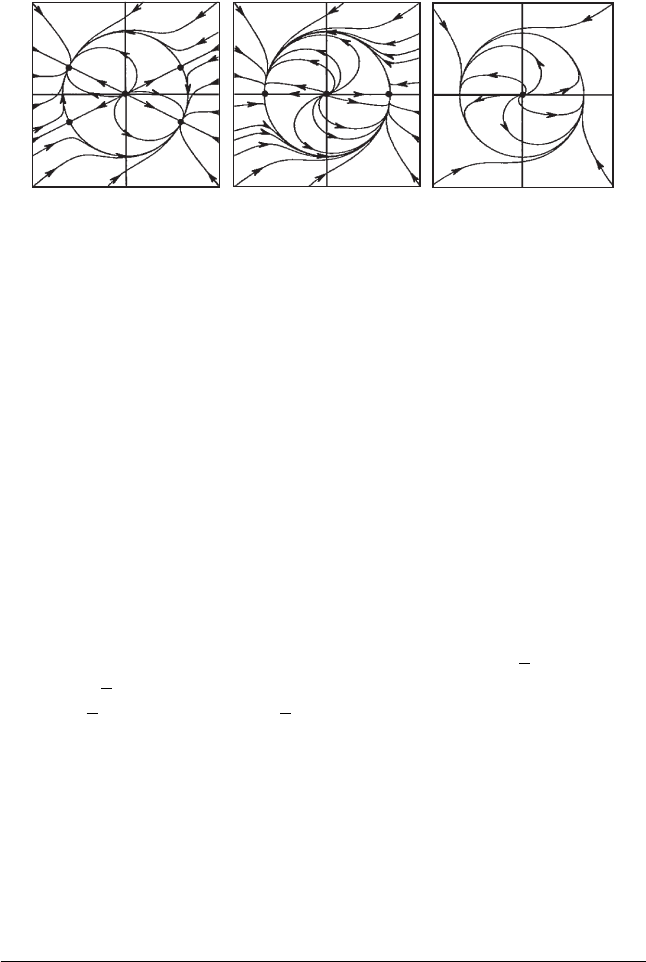
182 Chapter 8 Equilibria in Nonlinear Systems
Figure 8.9 Global effects of saddle-node bifurcations when, from left
to right, a <0,a =0,anda >0.
There is an equilibrium point at the origin and the linearized system is
X
=
a −1
1 a
X.
The eigenvalues are a ± i, so we expect a bifurcation when a = 0.
To see what happens as a passes through 0, we change to polar coordinates.
The system becomes
r
= ar − r
3
θ
= 1.
Note that the origin is the only equilibrium point for this system, since θ
= 0.
For a<0 the origin is a sink since ar − r
3
< 0 for all r>0. Thus all solutions
tend to the origin in this case. When a>0, the equilibrium becomes a source.
So what else happens? When a>0 we have r
= 0ifr =
√
a. So the circle
of radius
√
a is a periodic solution with period 2π . We also have r
> 0if
0 <r<
√
a, while r
< 0ifr>
√
a. Thus, all nonzero solutions spiral toward
this circular solution as t →∞.
This type of bifurcation is called a Hopf bifurcation. Thus at a Hopf
bifurcation, no new equilibria arise. Instead, a periodic solution is born
at the equilibrium point as a passes through the bifurcation value. See
Figure 8.10.
8.6 Exploration: Complex Vector Fields
In this exploration, you will investigate the behavior of systems of differential
equations in the complex plane of the form z
= F(z). Throughout this
section z will denote the complex number z = x + iy and F(z) will be a

8.6 Exploration: Complex Vector Fields 183
Figure 8.10 The Hopf bifurcation for a < 0 and
a >0.
polynomial with complex coefficients. Solutions of the differential equation
will be expressed as curves z(t ) = x(t ) + iy(t ) in the complex plane.
You should be familiar with complex functions such as the exponential, sine,
and cosine as well as with the process of taking complex square roots in order
to comprehend fully what you see below. Theoretically, you should also have
a grasp of complex analysis as well. However, all of the routine tricks from
integration of functions of real variables work just as well when integrating
with respect to z. You need not prove this, because you can always check the
validity of your solutions when you have completed the integrals.
1. Solve the equation z
= az where a is a complex number. What kind
of equilibrium points do you find at the origin for these differential
equations?
2. Solve each of the following complex differential equations and sketch the
phase portrait.
(a) z
= z
2
(b) z
= z
2
− 1
(c) z
= z
2
+ 1
3. For a complex polynomial F (z), the complex derivative is defined just as
the real derivative
F
(z
0
) = lim
z→z
0
F(z) − F (z
0
)
z − z
0
,
only this limit is evaluated along any smooth curve in
C that passes
through z
0
. This limit must exist and yield the same (complex) number
for each such curve. For polynomials, this is easily checked. Now write
F(x + iy) = u(x, y) + iv(x, y).

184 Chapter 8 Equilibria in Nonlinear Systems
Evaluate F
(z
0
) in terms of the derivatives of u and v by first taking the
limit along the horizontal line z
0
+t , and secondly along the vertical line
z
0
+it. Use this to conclude that, if the derivative exists, then we must have
∂u
∂x
=
∂v
∂y
and
∂u
∂y
=−
∂v
∂x
at every point in the plane. The equations are called the Cauchy-Riemann
equations.
4. Use the above observation to determine all possible types of equilibrium
points for complex vector fields.
5. Solve the equation
z
= (z − z
0
)(z − z
1
)
where z
0
, z
1
∈ C, and z
0
= z
1
. What types of equilibrium points occur
for different values of z
0
and z
1
?
6. Find a nonlinear change of variables that converts the previous system to
w
= αw with α ∈ C. Hint: Since the original system has two equilibrium
points and the linear system only one, the change of variables must send
one of the equilibrium points to ∞.
7. Classify all complex quadratic systems of the form
z
= z
2
+ az + b
where a, b ∈
C.
8. Consider the equation
z
= z
3
+ az
with a ∈
C. First use a computer to describe the phase portraits for these
systems. Then prove as much as you can about these systems and classify
them with respect to a.
9. Choose your own (nontrivial) family of complex functions depending on
a parameter a ∈
C and provide a complete analysis of the phase por-
traits for each a. Some neat families to consider include a exp z, a sin z,
or (z
2
+ a)(z
2
− a).
EXERCISES
1. For each of the following nonlinear systems,
(a) Find all of the equilibrium points and describe the behavior of the
associated linearized system.
Exercises 185
(b) Describe the phase portrait for the nonlinear system.
(c) Does the linearized system accurately describe the local behavior
near the equilibrium points?
(i) x
= sin x, y
= cos y
(ii) x
= x(x
2
+ y
2
), y
= y(x
2
+ y
2
)
(iii) x
= x + y
2
, y
= 2y
(iv) x
= y
2
, y
= y
(v) x
= x
2
, y
= y
2
2. Find a global change of coordinates that linearizes the system
x
= x + y
2
y
=−y
z
=−z + y
2
.
3. Consider a first-order differential equation
x
= f
a
(x)
for which f
a
(x
0
) = 0 and f
a
(x
0
) = 0. Prove that the differential equation
x
= f
a+
(x)
has an equilibrium point x
0
() where → x
0
() is a smooth function
satisfying x
0
(0) = x
0
for sufficiently small.
4. Find general conditions on the derivatives of f
a
(x) so that the equation
x
= f
a
(x)
undergoes a pitchfork bifurcation at a = a
0
. Prove that your conditions
lead to such a bifurcation.
5. Consider the system
x
= x
2
+ y
y
= x − y + a
where a is a parameter.
(a) Find all equilibrium points and compute the linearized equation at
each.
(b) Describe the behavior of the linearized system at each equilibrium
point.
