Hillert M. Phase Equilibria, Phase Diagrams and Phase Transformations: Their Thermodynamic Basis

Подождите немного. Документ загружается.

Projected and mixed phase diagrams

10.1 Schreinemakers’ projection of potential phase diagrams

Another method of reducing the number of axes is based on projection. By projecting all

the features onto one side of the phase diagram, one will retain all the features, but the fea-

tures of the highest dimensionality will no longer be visible because the dimensionality of

a geometrical element will decrease by one unit by projection and they may thus overlap

each other and also overlap features of the next-higher dimensionality. As an example,

Fig. 10.1(b) shows a P, T diagram obtained by projection of Fig. 8.11 (shown again as

Fig.10.1(a))inthe µ

direction. Such a P, T diagram is called Schreinemakers’ projection

[16]. In a system with c components it is obtained by projecting in the directions of c − 1

axes. It will show invariant equilibria with c + 2 phases as points, univariant equi-

libria with c + 1 phases as lines and in the angles between them there will be surfaces

representing divariant equilibria with c phases. Using a short-hand notation developed

by Schreinemakers, the coexistence lines for c − 1 phases are here identiﬁed also by

giving in parentheses the phases from the invariant equilibrium which do not take part.

Forexample, the (α) curve represents the α-absent equilibrium, i.e. β + γ + δ.Bycom-

parison with Fig. 10.1(a) it can be seen that the angle between (α) and (β)iscovered

by the γ + δ surface but also by the α + δ surface which extends to the (γ) line and by

the β + γ surface which extends to the (δ) line. The α one-phase ﬁeld covers the whole

diagram and the other one-phase ﬁelds each cover part of it.

Suppose we have a binary system with ﬁve phases, denoted 1, 2, 3, 4 and 5. An invariant

equilibrium would have four phases. Suppose the system shows two such equilibria and

by giving the absent phase they may be denoted (1) and (5). The complete phase diagram

would have three dimensions (same as for a one-phase ﬁeld). Projection would give just

one of the diagrams shown in Fig. 10.2 but by presenting two diagrams obtained by

projection in slightly different directions as a stereographic pair one can preserve the

three-dimensional information. It is thus evident that the apparent intersection between

the lines (1, 4) and (5, 3) is not an intersection in three dimensions. Therefore, it does

not represent an invariant equilibrium.

T, P diagrams obtained by projection are particularly useful for multinary systems and

are obtained by projecting in the direction of all the independent chemical potentials. We

shall return to such diagrams in Section 10.5 but ﬁrst we shall consider simpler cases.

In a projected diagram one sometimes includes a series of parallel sections drawn

with thinner lines. Such lines may be called equipotentials (or isotherms or isobars when

206 Projected and mixed phase diagrams

α+β+δ (γ)

β+γ+δ (α)

α+γ+δ (β)

α+β+γ (δ)

α+δ

γ+δ

β+γ

(a) (b)

Figure 10.1 (a) The binary potential phase diagram of Fig. 8.11 reproduced to illustrate the

projection in the µ

direction. (b) The diagram obtained by projection. The positions of some of

the two-phase surfaces are shown.

(5.3)

(1.4)

(5.4)

(5)

(1)

(1.5)

(1.3)

(1.2)

(5.2)

(5.3)

(1.4)

(1.3)

(5.4)

(1.5)

(1)

(5)

(1.2)

(5.2)

Figure 10.2 Stereographic pair of Schreinemakers’ projection of a binary system, showing the

three-dimensional shape. The phases not taking part in an equilibrium are given in parentheses.

It can be seen that lines (1.4) and (5.3) do not intersect.

appropriate). Such a section was presented in Fig. 8.12.Figure 10.3(b) shows a diagram

with several parallel sections. In order to simplify this picture, only the equilibria with

the δ phase are shown here. Arrows within the ﬁgure show the direction of decreasing

temperature.

Sometimes one uses both projecting and equipotential sectioning in order to reduce

the number of axes. One may be interested in the changes of various phase equilibria

with T and the chemical potential of some volatile component, e.g. oxygen, and one

is willing to limit the information by making an equipotential section at P = 1 bar.

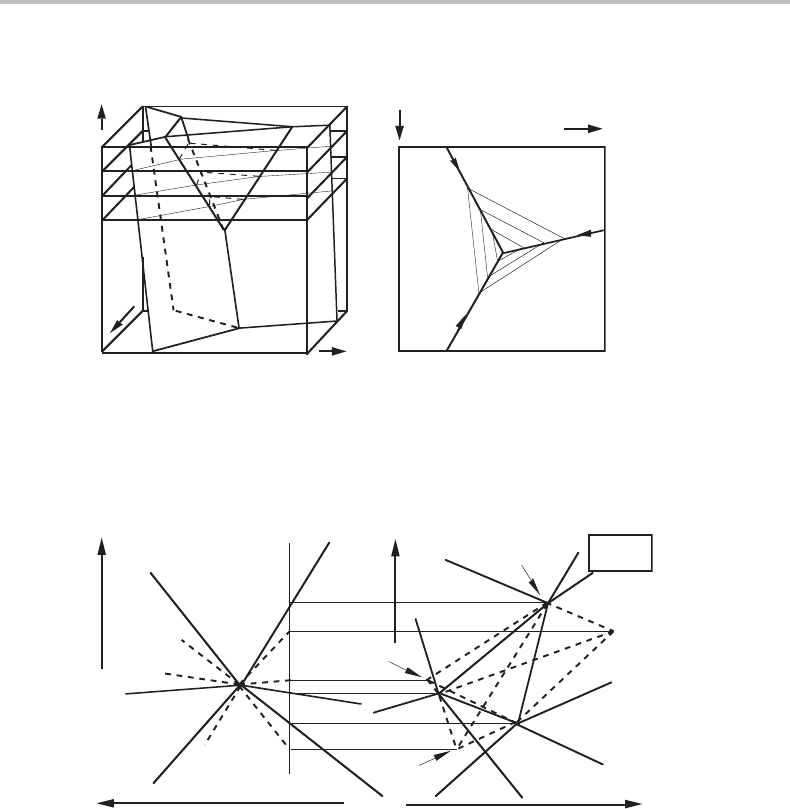
Figure 10.4 gives an illustration from a quaternary system. According to Gibbs’ phase

rule an invariant equilibrium is obtained with c + 2 = 6 phases for c = 4, and six uni-

variant equilibria should radiate from it. Let us denote the phases by 1 to 6. A section

at P = P

will cut through the lines (1), (2) and (3). They will thus appear as points in

the right-hand part where one of the projected axes, µ

,isnow shown. The surfaces

extending between the lines in the T, P diagram (see Fig. 10.1(b)) will appear as lines in

10.1 Schreinemakers’ projection of potential phase diagrams 207

(a) (b)

Figure 10.3 (a) Equipotential sections inserted in the potential phase diagram of Fig. 8.11.

(b) The projection of the same potential phase diagram with inserted equipotential sections of

the two-phase surfaces involving the δ phase.

(1)

(2)

(3)

(4)

(5)

(6)

(1.3)

(2.3)

(2.4)

(2.5)

(2.6)

(3.6)

P = P

(a) (b)

(1.5)

(1.4)

(1.6)

(1.2)

(3.4)

(3.5)

Figure 10.4 (a) Schreinemakers’ projection of a quaternary system. (b) Section at P = P

. The

new axis, µ

,isone of those projected in the T, P diagram.

the section. A major difference between the two diagrams is that in (a) all other potentials

were projected but in (b) one of them, P,was sectioned.

Exercise 10.1

Find the section of the 2 + 4 + 5 + 6 equilibrium in the T,µ

diagram of Fig. 10.4.

Then, ﬁnd its surface in the T, P diagram.

Hint

How would that equilibrium be denoted using the absent phases?

208 Projected and mixed phase diagrams

Solution

It would be (1.3). In the T,µ

diagram it is represented by a line between the points (1)

and (3). In the T, P diagram its surface covers the angle between the (1) and (3) lines.

Exercise 10.2

A series of Fe–Cr alloys are heat treated together in a ﬂowing gas of constant C and N

potentials. After heat treatment for a long time at 1273 K, it is sometimes found that

four phases are present but not all in the same specimen. The experiment is repeated

several times with different C and N potentials and in some of those experiments the

four phases are again found. It may be assumed that Cr is not transferred between the

alloys. Is it possible that the four phases are found in more than one experiment, i.e. at

different combinations of C and N potentials?

Hint

We may treat T and P as constant in addition to the potentials of C and N. With four

components we thus have the same situation as in a binary system at variable P and T.

We may use Fig. 10.1(b) and identify µ

with µ

, T with µ

and − P with µ

Solution

It is thus useful to look at a µ

,µ

diagram obtained by projection in the µ

direction.

Each experiment should be represented by a point in that diagram but individual spec-

imens would fall on different positions along the projected µ

axis, which may also

be regarded as a projection along the conjugate molar axis, z

according to Table 9.2.

Such a diagram is given in Fig. 10.1(b).Wecan see that all experiments falling between

lines (α) and (β)may cut through three two-phase surfaces, together involving all four

phases. With all such combinations of µ

and µ

we will cut through all four one-phase

ﬁelds in Fig. 10.1(a).Four phases can thus be found in several of the experiments with

different values of µ

and µ

10.2 The phase ﬁeld rule and projected diagrams

In Section 8.5 we derived the phase ﬁeld rule for equipotential sections. Expressed in

terms of the number of components, c,itwasgivenbyEq. (8.23) and in terms of the

number of axes in the diagram, r,byEq. (8.24)bythe use of r = c + 1 − n

. The rule

will now be extended to include projections as well. The dimensionality of phase ﬁelds

with a large number of phases will not change their dimensionality by projecting. For

example, the phase ﬁeld for an invariant equilibrium will still be a point, Eq. (8.23)would

still hold,

d = c + 2 − p − n

. (10.1)

10.2 The phase ﬁeld rule and projected diagrams 209

On the other hand, the dimensionality of the diagram would decrease by each projection,

yielding the following relation,

r = c + 1 − n

− n

. (10.2)

Inserting this in Eq. (8.23), here reproduced as Eq. (10.1), we obtain instead of Eq. (8.24),

d = υ − n

= c + 2 − p − n

= 1 + r − p + n

. (10.3)

The dimensionality of the diagram after a number of projections may have decreased to

the dimensionality of a phase ﬁeld, i.e. to r = d, and that happens when n

= p −1as

demonstrated by Eq. (10.3). Each further projection will decrease the dimensionalities

of the diagram and the phase ﬁeld by one unit because a feature in the diagram can never

have a higher dimensionality than the diagram itself. We thus ﬁnd that

d = r = c + 1 − n

− n

for n

≥ p −1. (10.4)

whereas Eq. (10.3) holds for n

≤ p −1.

A practical example is given in Fig. 10.5, concerning the Fe–O–S system. Since there

are four lines radiating from each point we may conclude that the invariant equilibria

concern four phases. The phase ﬁeld rule in Eq. (10.3)gives, for large p,

0 = c + 2 − p − n

= 3 + 2 − 4 − n

= r + 1 − p + n

= 2 + 1 − 4 + n

= 1; n

= 1.

It is evident that one has sectioned at a constant value of some potential, probably P at

1 bar. Then one has projected once, in the direction of µ

or µ

.However, it must be

remembered that the complete phase diagram was ﬁrst obtained from the fundamental

property diagram by projecting in the direction of some µ

, the one which was consid-

ered as the dependent variable. Figure 10.5 has thus been obtained from the fundamental

property diagram by projecting twice, and sectioning once, and it does not matter which

projection was made ﬁrst, µ

or µ

.Itshould be emphasized that n

represents the num-

ber of projections of the complete phase diagram. The ﬁrst projection of the fundamental

property diagram is not included in n

It is interesting to note that the two three-phase lines h (FeO +Fe

+ L) and

f(Fe+ FeO + L) stop inside the diagram. They stop at invariant three-phase points

in the binary Fe–O system which overlaps the diagram. In principle, the whole surface

of the diagram is covered by the binary Fe–O diagram which may be regarded as the

bottom plate of the three-dimensional phase diagram, where µ

=−∞, assuming that

the fundamental property diagram was ﬁrst projected in the µ

direction to give a phase

diagram. On the bottom plate, there is no S and the number of components c is thus 2

instead of 3. Three-phase equilibria would thus appear as points and two-phase equi-

libria as lines. That bottom plate is shown in (b) but was not included in (a) because

210 Projected and mixed phase diagrams

(a)

−200

−300

−400

1000 1500 1000 1500

(b)

Temperature (K)

RT InP

(kJ)

Temperature (K)

Fe+Fe

Fe+L

FeO

FeO +Fe

III

Figure 10.5 (a) Projected and sectioned (P = 1bar) phase diagram for the Fe–O–S system.

(a) Fe + Fe

+ FeS; (b) FeO + Fe

+ FeS; (c) Fe + FeO + FeS; (d) FeO +FeS + L;

(e) Fe + FeS + L; (f) Fe + FeO + L; (g) Fe

+ FeS + L; (h) FeO + Fe

+ L. The invariant

four-phase equilibria are (I) Fe + FeO + Fe

+ FeS; (II) Fe + FeO + FeS + L; (III)

FeO + Fe

+ FeS + L. (b) The Fe–O bottom plate.

−5

−10

−15

−25 −20 −15 −10 −5 −20 −15 −10 −5

logP

MnS

MnO

MnSO

(a) (b)

Figure 10.6 Potential phase diagram for (a) Cu−O−S and (b) Mn−O−Sat1bar and 1000 K.

These phase diagrams are two-dimensional and are not projections.

it would have made the diagram difﬁcult to interpret. Only the binary end-points for

FeO + Fe

+ L and Fe + FeO + Lwere marked.

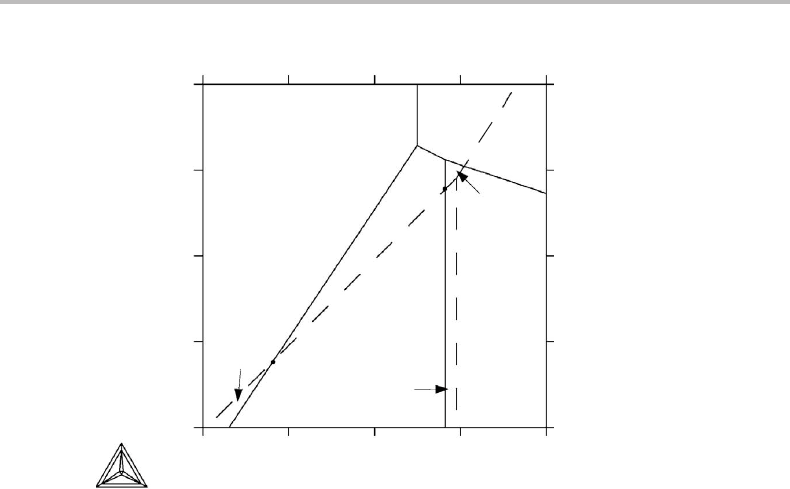
In many cases one should consider the top plate as well as the bottom plate. A

log P

, log P

diagram of the Cu–Mn–O–S system under P = 1 bar and T = 1000

Kwould be an example. The top and bottom would represent the Cu–O–S and Mn–O–S

systems, respectively, if the projected axis is taken as (µ

− µ

). These diagrams are

given in Fig. 10.6.

The solubilities of Cu in the Mn phases and of Mn in the Cu phases are all very

low. The equilibria between the Cu–O–S phases will not be affected by the presence

10.2 The phase ﬁeld rule and projected diagrams 211

−5

−10

−15

−25 −20 −15 −10 −5

MnS + Cu

+ MnSO

MnO+Cu

+Cu

MnSO

+Cu

MnS

+Cu

MnO

logP

Figure 10.7 Projected phase diagram for Cu–Mn–O–S at 1 bar and 1000 K. For clarity, all the

lines from the Cu–O–S side are presented with dashed lines here.

of Mn, nor the Mn–O–S phases by Cu. Both diagrams can thus be plotted in the same

RT ln P

, RT ln P

coordinate frame to form the Cu−Mn−O−S diagram (Fig. 10.7).

The lines in the ternary systems can be copied into the quaternary system and they

become surfaces in the projected direction and still appear as lines in the Cu–Mn–O–S

diagram. New two-phase surfaces form between the previous one-phase ﬁelds and they

are identiﬁed in the diagram.

An interesting question is the choice of projected axis in Fig. 10.7.Inorder to treat Cu

and Mn in a symmetric way, it is convenient to consider (µ

+ µ

)asthe projected axis

to give a phase diagram from the fundamental property diagram and then (µ

− µ

)

as the axis used for projection of the phase diagram to reduce the number of axes to two.

Exercise 10.3

Only three lines intersect at the invariant equilibrium I in Fig. 10.5. What line is not

shown and why not?

Hint

The fourth line should be the one without FeS.

Solution

The Fe + FeO + Fe

line is not shown because one has projected the diagram exactly

in its direction and the line thus appears as a point. The reason is that the projection has

212 Projected and mixed phase diagrams

been made in the µ

direction and S does not dissolve in any one of these three phases.

Thus, the equilibrium Fe + FeO + Fe

is not affected by S and its line goes exactly in

the µ

direction. It exists at a certain T, P

, only, and it is shown in the binary Fe−O

diagram in Fig. 10.5(b).

Exercise 10.4

At 1000 K one measures the emf of an electrolytic cell where one electrode is a mixture

of MnS, MnO, Cu

S and Cu and the other is a mixture of Cu

O and Cu. The electrolyte

is solid zirconia stabilized with calcia. Use Fig. 10.7 to estimate the resulting emf.

Hint

The electrical current can pass through this electrolyte mainly by the diffusion of

−2

ions. The emf will thus be an expression of the difference in oxygen potential

between the two electrodes and it can be estimated from the difference in RT ln P

for

two points in the diagram representing the electrodes.

Solution

The point for Cu

O + Cu can be taken anywhere on the corresponding line yield-

ing log P

=−10.2inFig.10.6(a) (also dashed line in Fig. 10.7). The other point

is obtained as the intersection between two lines in the lower left part of Fig. 10.7

and yields log P

=−21.2. We get µ

= 0.5µ

= 0.5RT (1n P



− 1n P



) =

0.5RT 1n 10 ·(−10.2 + 21.2) = 12.7 RT. Remembering that the O ion is divalent we

get E · 27 = µ

where 7 is Faraday’s constant (96 486 coulomb/mole) and thus E =

0.547 V.

10.3 Relation between molar diagrams and Schreinemakers’

projected diagrams

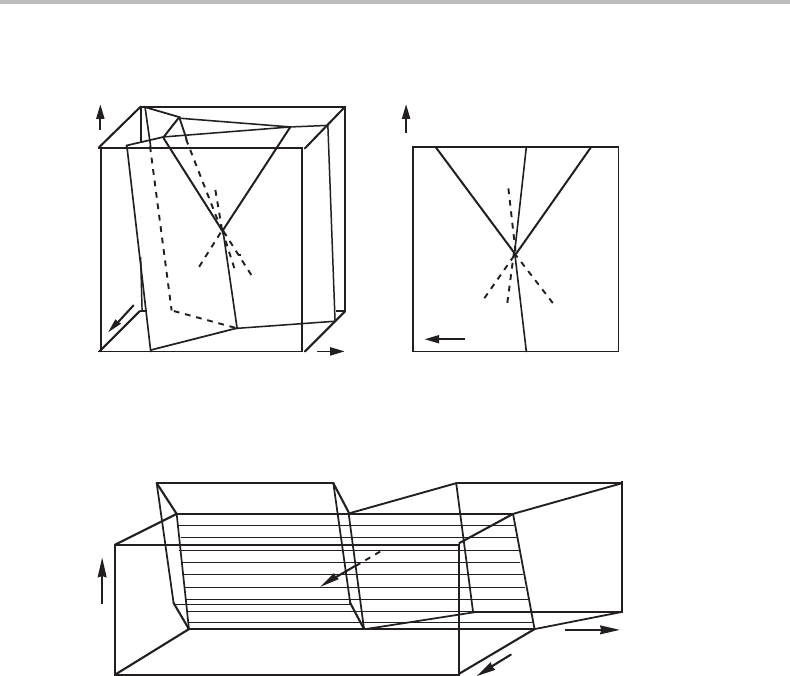
As demonstrated byFigs.8.7 and 8.11, the elementary units of potential diagrams are very

simple from the topological point of view. In this sense, the projections of such diagrams

are more interesting. This is evident if one considers the dashed extrapolations shown in

the projected diagram in Fig. 10.8(b). Between the lines there are two extrapolations in

one case, one extrapolation in two cases, and no extrapolation in one case. In fact, this

is the only way to draw four lines in different directions if the 180

◦

rule is to be obeyed.

It is evident that, in the projected direction, the four phases are related to each other in a

special way. This phenomenon will now be examined. In order to simplify the discussion

the method of identifying a univariant line by giving within parentheses the absent phase

is used in Fig. 10.8(b).

If potential axes are chosen for plotting the complete, three-dimensional phase diagram

of a binary system, the four phases of an invariant equilibrium will fall on one point. If

10.3 Relation between molar and Schreinemakers’ projected diagrams 213

(γ)

(α)

(β)

(δ)

(a) (b)

Figure 10.8 (a) Binary phase diagram and (b) projection in the µ

direction, taken from

Fig. 10.1. The extrapolations of the three-phase lines are marked with dashed lines.

Figure 10.9 Introduction of a molar axis into the potential diagram of Fig. 10.8. Only the lower

half of that diagram is used here. The surface marked with horizontal tie-lines represents the

α + β + γ equilibrium.

one molar quantity is introduced, say, instead of Y

, then the four phases will fall on a

line, just as the three phases in the three-phase equilibrium in Fig. 9.2(a) fall on a line

in Fig. 9.2(b).Inthat case, it is easy to see the order in which the phases are arranged

along the line. The hcp phase must be placed between bcc and fcc. Otherwise, there

would be some overlapping of the one-phase ﬁelds which is not allowed according to

Section 9.1. Using the same reasoning, it is easy to see the order in which the four phases

of Fig. 10.8 will be arranged when a molar quantity is introduced. One simply looks at

the direction of the two-phase surfaces. Each one will turn into a two-phase volume when

is introduced instead of the µ

axis. In Fig. 10.9 these volumes are demonstrated for

the three surfaces between α, β and γ.Itisevident that γ must fall between α and β

along the z

axis.

When the phase diagram of Fig. 10.8(a) is projected in the µ

direction and

Fig. 10.8(b) is formed, much information is lost. However, the information regarding the

order of arrangement along the projected direction, obtained when the molar quantity is

introduced, is not lost. This is because some conclusions can still be drawn regarding the

directions of the two-phase surfaces. They are situated between the three-phase lines.

214 Projected and mixed phase diagrams

Figure 10.10 One-dimensional molar phase diagram at constant T and P, showing the relative

position of four phases along the z

axis, introduced instead of a µ

axis, through the invariant

equilibrium in Fig. 10.8(a). The composition is here expressed with the z

variable because it is

the conjugate variable to µ

according to Table 9.2. The relative positions of all the four phases

along a z

axis, going through the invariant phase equilibrium are demonstrated schematically in

Fig. 10.3.

This was demonstrated in Fig. 10.1(a).Itisthus possible to get an impression of the

relative positions of the six surfaces and thus of the relative positions of the phases along

the molar axis of the projection.

The simplest method to interpret an experimental diagram like Fig. 10.8(b) is to

draw the four extrapolations and then turn the diagram in the same way as Fig. 10.8(b)

with respect to the dashed extrapolations. The compositions of the phases will then be

arranged in the order given by Fig. 10.10 or in the completely reverse order. A more

logical method will be described in the following section.

Exercise 10.5

In Exercise 10.2 we considered a heat treatment of several Fe–Cr specimens under

carburizing and nitriding conditions at constant T and P. It had been found that four

phases could be present in some experiments but not in the same specimen. Now try to

ﬁnd what is the maximum number of phases in any one specimen.

Hint

As already explained, we can use Fig. 10.1(b) because our quaternary system at constant

T and P behaves like a binary system at variable T and P.Inour case the two axes should

be µ

and µ

and the projection has been made in the direction of µ

,which is the

same as the direction of z

Solution

In Exercise 10.2 we saw that four phases can be present if µ

and µ

fall between

the lines (α) and (β)inFig. 10.1. The specimens fall on different positions along the

projected axis. Most of them may fall between the surfaces representing two phases and

they will thus have only one phase. What is the chance that some fall on the two-phase

surface? Since the specimens are deﬁned by their contents of Cr we should regard the

projected molar axis rather than the potential axis. The two-phase surface in the potential

diagram has a thickness when the molar axis has been introduced. There is thus deﬁnite

chance that a specimen falls within the two-phase region.