Hillert M. Phase Equilibria, Phase Diagrams and Phase Transformations: Their Thermodynamic Basis

Подождите немного. Документ загружается.

Molar phase diagrams

9.1 Molar axes

If one starts from a potential phase diagram, one may decide to replace one of the poten-

tials by its conjugate variable. However, the potential phase diagram has no information

on the size of the system and one should thus accept introducing a molar quantity rather

than its extensive variable. By replacing all the potentials with their conjugate molar

variables, one gets a molar diagram. One would like to retain the diagram’s character

of a true phase diagram, which means that there should be a unique answer as to which

phase or phases are stable at each location. In this chapter we shall examine the properties

of molar diagrams and we shall ﬁnd under what conditions they are true phase diagrams.

Only then may they be called molar phase diagrams.However, we shall start with a

simple demonstration of how a diagram changes when molar axes are introduced.

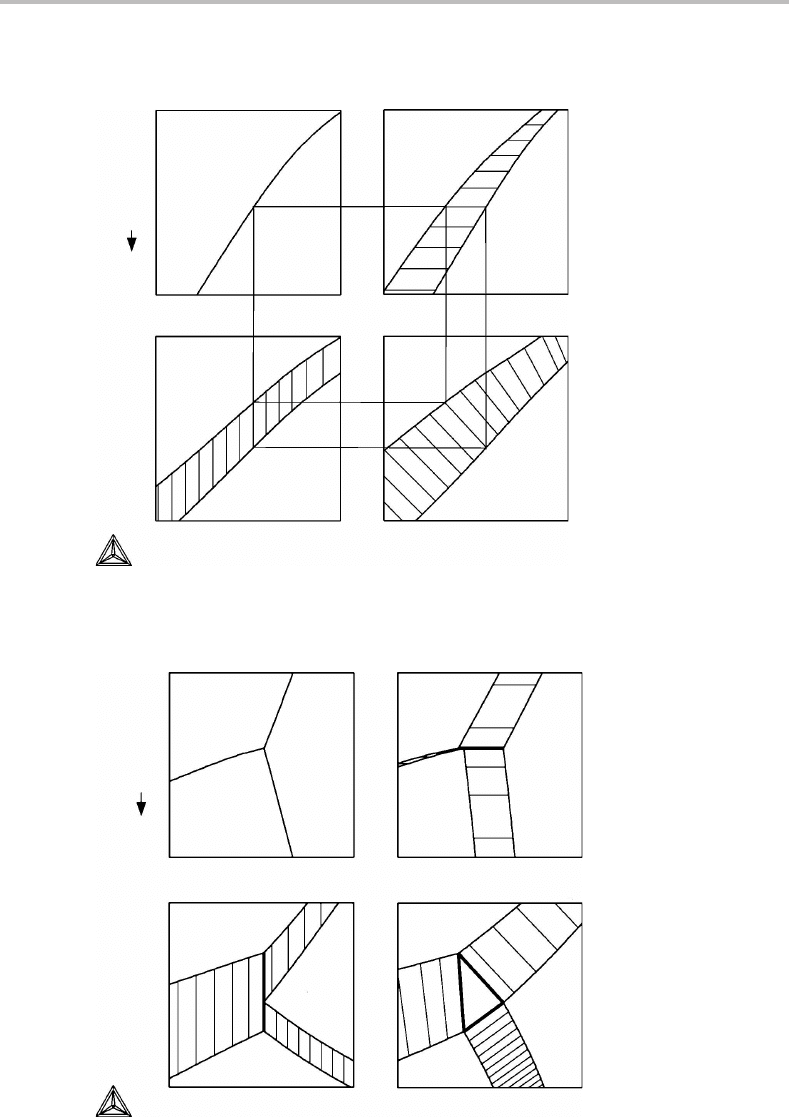
Figure 9.1(a)–(d) demonstrates what happens to a part of the T , P potential phase

diagram for Fe when S

and V

axes are introduced. Initially the P axis is plotted in the

negative direction because V is conjugate to −P. It can be seen that the one-phase ﬁelds

separate and leave room for a two-phase ﬁeld. It can be ﬁlled with tie-lines connecting the

points representing the individual phases in the two-phase equilibrium. It is self-evident

how to draw them when one axis is still a potential but they yield additional information

when all axes are molar (Fig. 9.1(d)).

Figure 9.2(a)–(d) is a similar demonstration using a part of the Fe phase diagram with

a three-phase equilibrium, a triple point. It forms a tie-triangle when both potentials

have been replaced (Fig. 9.2(d)). All the phase ﬁelds are then two-dimensional. One may

also notice that each one-phase ﬁeld from the potential diagram maintains its general

shape. Their corners still have angles less than 180

◦

(see the 180

◦

rule formulated in

Section 8.3).

It should be emphasized that the phase ﬁelds never overlap in these diagrams. They

may all be classiﬁed as true phase diagrams because each point represents one and only

one phase equilibrium. Three requirements must be fulﬁlled in order for this to happen.

Firstly, the two one-phase ﬁelds meeting at a two-phase line in a potential phase diagram

must move away from each other and leave room for an extended two-phase ﬁeld, when

a molar axis is introduced. Secondly, the one-phase ﬁeld extending from the two-phase

ﬁeld in the direction of increasing values of a potential must also extend to increasing

values of the conjugate molar variable that is introduced. If it goes the other way, it

would overlap the two-phase region. The other one-phase ﬁeld must extend in the other

186 Molar phase diagrams

(a) (b)

800 1100 58 74

(J/mol K)

bcc

P (kbar)

T (K)

fcc

bcc

⋅ 10

)

fcc

bcc

fcc

bcc

fcc

Figure 9.1 Introduction of molar axes instead of potential axes in a part of the unary phase

diagram for Fe with two phases.

(a) (b)

140

500 1000 45 65

(J/mol K)

bcc

P (kbar)

T (K)

fcchcp hcp

bcc

⋅ 10

)

fcc

hcp

bcc

fcc

hcp

bcc

fcc

Figure 9.2 Introduction of molar axes instead of potential axes in a part of the unary phase

diagram for Fe with three phases. All phase ﬁelds here become two-dimensional.

9.1 Molar axes 187

−28 −26 −24

Helmholtz energy (kJ/mol)

Entropy (J/molK)

−22 −20

hcp

fcc

bcc

Figure 9.3 S, H diagram for Fe. This is not a true phase diagram because S and H never appear in

the same set of conjugate variables.

direction, before as well as after replacing the potential with the conjugate molar variable.

Thirdly, a one-phase ﬁeld is nowhere allowed to fold over itself.

The last two requirements are fulﬁlled if the system is everywhere stable because of

the stability condition from Eq. (6.28),



∂Y

∂ X



> 0. (9.1)

The potential Y

and its conjugate variable X

thus increase in the same direction.

However, as already emphasized, this stability condition requires that all the variables to

be kept constant, here represented by Y

, come from the same set of conjugate pairs

as Y

and X

. Nine such sets were presented in Table 3.1 but it is necessary to examine

what happens to them when the size of the system is measured in different ways. This

will be discussed in the next section. Figure 9.3 is an example of what can happen if

one uses two molar variables which do not appear in the same set of conjugate variables,

S and H. It is not a true phase diagram according to the deﬁnition given at the very

beginning of this section. Other cases will be discussed in Section 10.7.

The ﬁrst requirement can be tested as follows, using the form of the Gibbs–Duhem

relation with molar quantities introduced in Eq. (8.4),

dµ

=−S

dT + V

dP −



dµ

=−

c+2



. (9.2)

Consider two phases, α and β,which are initially in equilibrium with each other. The

system is then moved away from equilibrium by changing the value of one poten-

tial, Y

,keeping the other independent potentials in the summation constant. Apply-

ing the Gibbs–Duhem relation to each of the two phases and taking the difference, we

obtain



− µ





jα

− X

jβ



. (9.3)

188 Molar phase diagrams

Figure 9.4 Four-phase equilibrium in a phase diagram with three molar axes. The four-phase

ﬁeld is tetrahedral and is covered by triangular prisms representing three-phase equilibria. The

two- and one-phase ﬁelds are not outlined but they are also three-dimensional.

Suppose α is the phase favoured by the increased Y

value. Then µ

must be smaller

than µ

as demonstrated by Fig. 8.3.Wethus obtain

jα

− X

jβ



− µ



> 0. (9.4)

It is thus evident that the two one-phase ﬁelds will move apart by a positive distance

jα

− X

jβ

when X

is introduced as an axis instead of Y

. The one-phase ﬁelds will

separate and give room for the two-phase ﬁeld in between, X

jα

− X

jβ

being the length

of the tie-line.

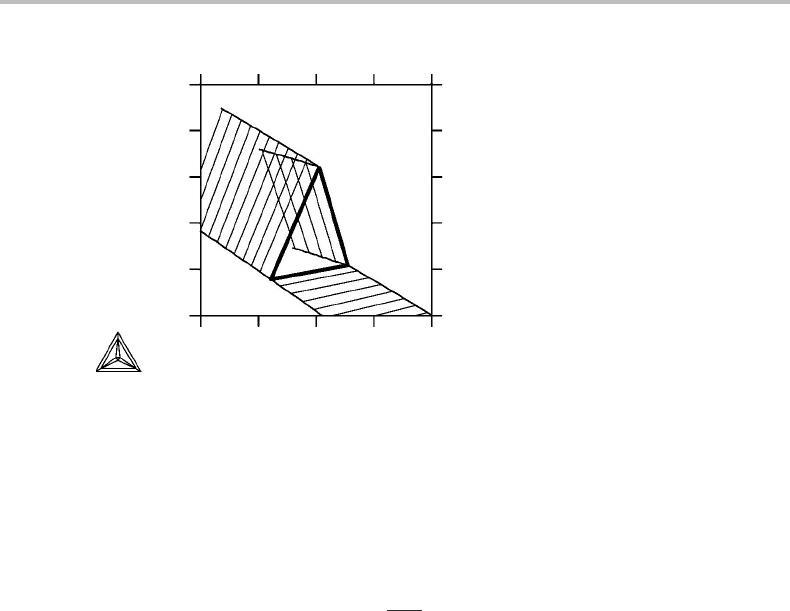
In a binary system there are three independent potential axes. If they are all replaced

by molar axes, all the phase ﬁelds become three-dimensional and the invariant four-

phase equilibrium expands into a tetrahedron. This is demonstrated by Fig. 9.4 which

corresponds to the central region of Fig. 8.11.

It was emphasized that the topology of potential phase diagrams is very simple and

each geometrical element is a phase ﬁeld. A phase diagram with only molar axes has

a relatively simple topology. All the phase ﬁelds have the same dimensionality as the

diagram itself. For the unary system in Fig. 9.2 all the phase ﬁelds have two dimensions

and for the binary system in Fig. 9.4 they have three dimensions.

Exercise 9.1

Suppose one studies the total vapour pressure of a liquid mixture of two metals, A and

B, at a constant temperature. One ﬁnds that the total vapour pressure increases if more

Bisadded to the mixture. Show whether the vapour or the liquid is richer in B.

9.2 Sets of conjugate pairs containing molar variables 189

before

(a) (b)

vapour

liquid

after

Figure 9.5 Solution to Exercise 9.1.

Hint

At constant T, the P, µ

potential phase diagram will be two-dimensional. Sketch it

using µ

as the dependent potential variable. Remember that the conjugate composition

variable to µ

would then be z

= N

. High pressure should favour the liquid, being

much denser than the vapour.

Solution

The construction (Fig. 9.5) shows that the vapour would be richer in B than the liquid if

measured relative to A.

9.2 Sets of conjugate pairs containing molar variables

A molar variable can easily be introduced in the stability condition, Eq. (6.28), by dividing

with the quantity used to deﬁne the size of the system because that quantity is kept

constant. Expressing the size by N,weget for instance,



∂Y

∂ X



= N ·



∂Y

∂ X



> 0. (9.5)

However, with this measure of size the Gibbs–Duhem relation gives

dT − V

dP +



dµ

= 0, (9.6)

where one of the x

is dependent on the others because



= 1. Choosing x

as the

dependent one, we obtain x

= 1 −



− dµ

= S

dT − V

dP +



d(µ

− µ

). (9.7)

Then it is logical to regard µ

as the dependent potential but the consequence is that the

conjugate variable to x

is no longer µ

but (µ

− µ

If we instead measure the size with the amount of a certain component, N

, then we

obtain the form given by Eq. (9.2),

− dµ

= S

dT − V

dP +



dµ

. (9.8)

190 Molar phase diagrams

Table 9.1 Sets of conjugate pairs of independent state variables using

molar quantities defined by dividing with  N

T, S

−P, V



(µ

− µ

), x

T, (TS

− PV

)/T −P/T, TV



(µ

− µ

), x

T/P, PS

P, (TS

− PV

)/P



(µ

− µ

), x

−1/T, U

−P/T, V



(µ

− µ

)/T, x

−1/T, H

−P, V



(µ

− µ

)/T, x

−P/T, H

/P −1/P, PU



(µ

− µ

)/T, x

T/P, S

−1/P, U



(µ

− µ

)/P, x

−1/T, TU

/P −T /P, F



(µ

− µ

)/P, x

T, S

/P −1/P, F



(µ

− µ

)/P, x

In this way one may keep µ

but its conjugate variable is z

= N

and S

and V

are also deﬁned by dividing with N

Sometimes it is convenient to measure the size as the total content of more than one

component, e.g. of those which do not easily evaporate. Suppose they are the ﬁrst k

components. Using u

= 1 −



we obtain

m(1...k)

dT − V

m(1...k)

dP +



i(1...k)

dµ

= 0 (9.9)

−dµ

= S

m(1...k)

dT − V

m(1...k)

dP +



i(1...k)

d(µ

− µ



k+1

i(1...k)

dµ

= 0.

(9.10)

where the S, V and u variables are deﬁned in Section 4.3.

These three methods of measuring the size of the system can be applied to all the

rows in Table 3.1.Wemay thus construct Tables 9.1, 9.2 and 9.3 for the sets of conjugate

potentials and molar variables. Each row deﬁnes a set of conjugate variables and each

pair can be used to construct a stability condition if the variables to be kept constant are

taken from the same set. There is an important difference from Table 3.1 which gave

sets of conjugate pairs related by the Gibbs–Duhem relation. A dependent potential has

now been eliminated using the Gibbs–Duhem relation and the new tables contain one

pair less and give sets of pairs of independent variables.

9.2 Sets of conjugate pairs containing molar variables 191

Table 9.2 Sets of conjugate pairs of independent state variables using

molar quantities defined by dividing with N

T, S

−P, V



, z

T, (TS

− PV

)/T −P/T, TV



, z

T/P, PS

P, (TS

− PV

)/P



, z

−1/T, U

−P/T, V



/T, z

−1/T, H

−P, V



/T, z

−P/T, H

/P −1/P, PU



/T, z

T/P, S

−1/P, U



/P, z

−1/T, TU

/P −T /P, F



/P, z

T, S

/P −1/P, F



/P, z

Table 9.3 Sets of conjugate pairs of independent state variables using molar quantities defined by

dividing with N

+ N

T, S

m12

−P, V

m12

(µ

− µ

), u

i(12)



, u

i(12)

T, (TS

m12

− PV

m12

)/T −P/T, TV

m12

(µ

− µ

), u

i(12)



, u

i(12)

T/P, PS

m12

P, (TS

m12

− PV

m12

)/P (µ

− µ

), u

i(12)



, u

i(12)

−1/T, U

m12

−P/T, V

m12

(µ

− µ

)/T, u

i(12)



/T, u

i(12)

−1/T, H

m12

−P, V

m12

/T (µ

− µ

)/T, u

i(12)



/T, u

i(12)

−P/T, H

m12

/P −1/P, PU

m12

/T (µ

− µ

)/T, u

i(12)



/T, u

i(12)

T/P, S

m12

−1/P, U

m12

(µ

− µ

)/P, u

i(12)



/P, u

i(12)

−1/T, TU

m12

/P −T /P, F

m12

/T (µ

− µ

)/P, u

i(12)



/P, u

i(12)

T, S

m12

/P −1/P, F

m12

(µ

− µ

)/P, u

i(12)



/P, u

i(12)

192 Molar phase diagrams

3000

(a) (b)

log(P

) (bar)

−60

log(x

)

L/α

α/L

α/Mo

N/α

L/Mo

N/L

1000

500

100

1 bar

2500

2000

T (K)

1500

1000

0 0.5

Figure 9.6 See Exercise 9.3.

Exercise 9.2

At the end of Section 6.6 we found that the stability limit in a binary solution is g

= 0.

Show how this condition can be obtained from the list of conjugate variables presented

in Table 9.1.

Hint

The index 2 in g

indicates a derivative with respect to x

, with x

as a dependent

variable. Thus, one should use a set of conjugate variables containing x

Solution

From the ﬁrst row of Table 9.1 we can formulate the condition (∂(µ

− µ

)/∂x

)

T,P,N

0. However, x

is a dependent variable and µ

− µ

= ∂G

/∂x

and our stabil-

ity condition can be expressed as ∂

/∂x

= 0 and g

is the notation for that

derivative.

Exercise 9.3

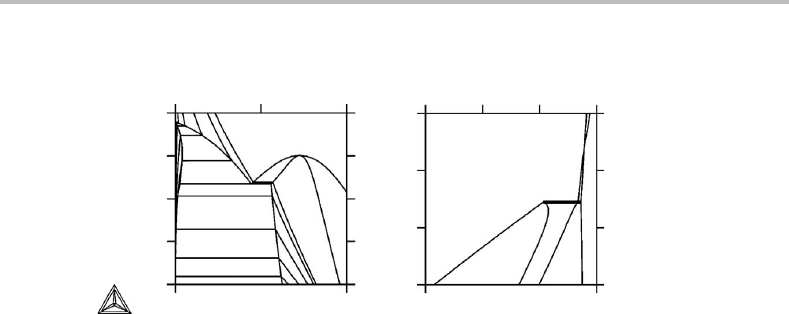
Two diagrams of the Mo–N system are presented in Fig. 9.6.How would you interpret

them?

Hint

In diagram (a) notice that the phase ﬁeld for the gas is not included but isobars for the N

gas are given. In order to interpret diagram (b) it is helpful ﬁrst to construct a T, log P

diagram and then replace the T axis with a log x

axis.

Solution

Diagram (a) above is a T, x

diagram at 1 bar. The lines for various N

pressures should

be understood as isoactivity lines for N expressed as P

of a gas which is not present.

9.3 Phase boundaries 193

(a) (b)

log(P

) (bar)

−60

log(x

)

L/α

α/L

α/Mo

N/α

L/Mo

N/L

log(P

) (bar)

3000 10002000

T (K)

Figure 9.7 Solution to Exercise 9.3.

(a) (b)

Figure 9.8 (a) Elementary unit of a phase diagram with two molar axes. (b) Topological

equivalence.

Using these values of P

it is easy to construct a T , log P

diagram (see Fig. 9.7(a)).

For convenience, we shall make T the abscissa. Next we shall introduce x

(with a

logarithmic scale) instead of T, i.e. a molar quantity instead of a potential. The two-

phase ﬁelds will open up but there may be overlapping because the new variable, x

,is

not conjugate to the old one, T. As an example, the α + L ﬁeld falls inside the α + Mo

ﬁeld.

9.3 Phase boundaries

Since all the phase ﬁelds in a molar diagram have the same dimensionality as the diagram

has axes, it is evident that all other geometrical elements, surfaces, line and points in

a three-dimensional diagram, are not phase ﬁelds. They separate phase ﬁelds and may

be called phase boundaries. When discussing the topology of a molar phase diagram

in terms of the phase boundaries, it is possible and convenient to choose a smaller

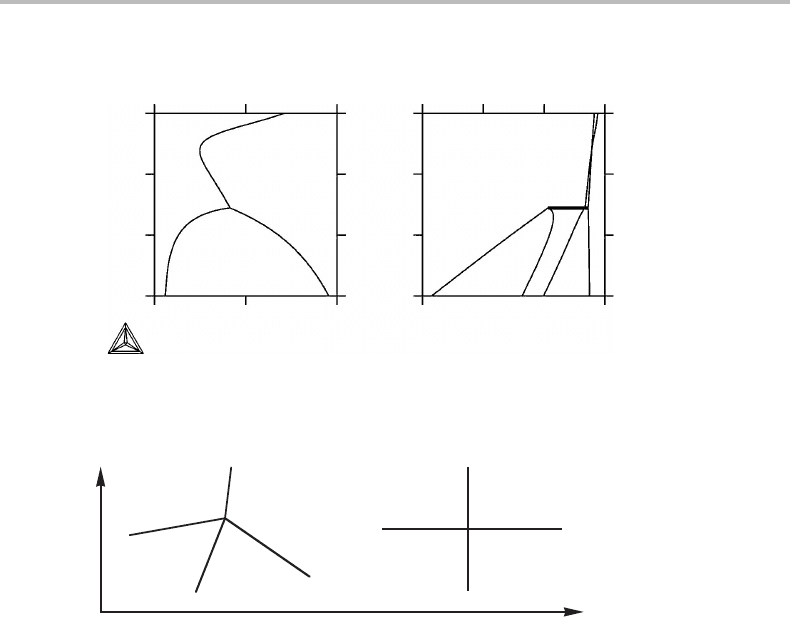
elementary unit than a phase ﬁeld. A smaller unit is shown in Fig. 9.8(a) and it is

composed of four linear phase boundaries meeting at a point. Topologically it may be

represented by two intersecting lines as shown in Fig. 9.8(b).Any complicated two-

dimensional phase diagram with molar axes is composed of such units.

194 Molar phase diagrams

Figure 9.9 Elementary unit of a phase diagram with three molar axes.

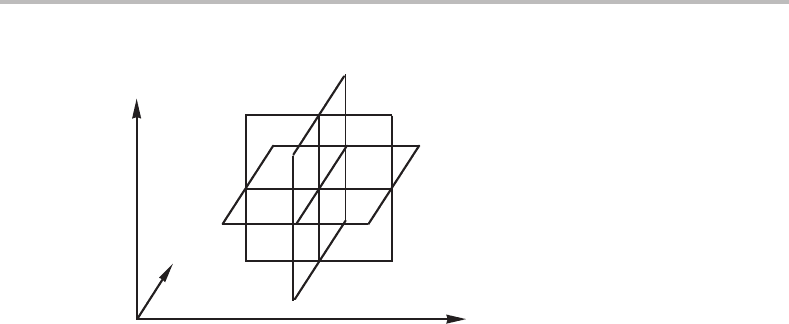
It can be seen by inspection of the three-dimensional diagram in Fig. 9.4, that it

is possible to divide it into four topologically identical, elementary units, each one

composed of a point where eight phase ﬁelds meet, although only four of them are shown.

Six linear phase boundaries radiate from these points. They are all shown for the β and

δ points. Topologically, this elementary unit can be represented by three intersecting

planes as shown in Fig. 9.9. Evidently, the topology of a complicated three-dimensional

molar diagram can be represented by a system of intersecting surfaces.

When studying two-dimensional molar diagrams, Masing [11] observed that the num-

ber of phases in the phase ﬁelds changes by one unit when one crosses a linear phase

boundary. This is easily veriﬁed by inspection of Fig. 9.2(d). Masing’s rule was later

generalized by Palatnik and Landau [12]who gave it the following form

+ D

−

= r − b, (9.11)

where D

and D

−

are the number of phases that appear and disappear, respectively, as

one crosses a phase boundary of dimensionality b, and r is the number of axes in the

molar diagram. This rule may be referred to as the MPL boundary rule, after Masing,

Palatnik and Landau.

It may be added that phase boundaries sometimes have special names. The boundary

between a liquid phase and a liquid + solid phase ﬁeld is called the liquidus and the

corresponding boundary for the coexistingsolid phase is called the solidus. The boundary

between a solid and the two-phase ﬁeld with another solid is sometimes called the solvus.

Exercise 9.4

In the central region of Fig. 9.4 there is a tetrahedron, representing a four-phase ﬁeld.

Apply the MPL rule in order to ﬁnd how many phases there are outside the α − β line

and outside the β point.

Hint

There are only four phases in the system and D

must be zero when we move out from

the four-phase ﬁeld because there is no new phase that can be added.