Hillert M. Phase Equilibria, Phase Diagrams and Phase Transformations: Their Thermodynamic Basis

Подождите немного. Документ загружается.

10.4 Coincidence of projected surfaces 215

(γ)

(α)

(β)

(δ)

(α)

(δ)

(a) (b)

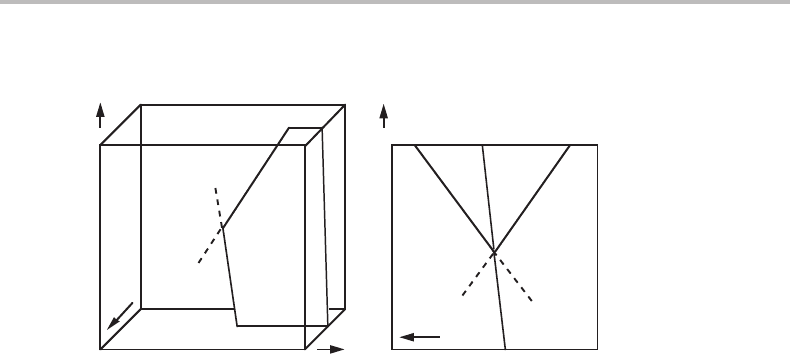
Figure 10.11 Modiﬁcation of Fig. 10.8 by rotation of the β + γ surface until it is parallel to the

axis. In the µ

projection the β + γ + δ(α) and α + β + γ + (δ) lines will now coincide

and their extrapolations will not be visible.

On the other hand, if predetermined amounts of C and N are added to a set of specimens

in a capsule, then one could not use Fig. 10.1(b) directly. For each specimen one should

rather consider a molar diagram like Fig. 9.4 and it is evident that the four phases could

occur in the same specimen and this could even happen in more than one specimen in

the same experiment.

10.4 Coincidence of projected surfaces

The method to determine the relative compositions of phases, now to be described, can

be used in higher-order systems as demonstrated in the next section, but a binary system

will be considered ﬁrst.

Suppose one could gradually change the properties of the system in such a way that

the β + γ surface in Fig. 10.8 would rotate around an axis roughly parallel to the T axis.

One could thus make the two lines (α) and (δ)inthe projection approach each other

without changing the topology of the projected diagram. At the moment of coincidence,

one has a situation such as that illustrated in Fig. 10.11.

The β + γ surface is now parallel to the direction of projection, µ

, and a continued

rotation would put the β + γ surface on the other side of the (α) and (δ) lines. Thus,

β and γ would be transposed in Fig. 10.10.Itispossible to conclude that the β and γ

phases have the same value of z

if the µ

projections of the (δ) and (α) lines coincide

when they meet at the four-phase point. Evidently, before the gradual rotation the β and

γ phases must have been neighbours along the z

line in Fig. 10.10. When the lines

coincide, the phases fall on the same point on the z

axis. This rule of coincidence is

closely related to Konovalov’s rule which will be discussed in Section 10.8. The relative

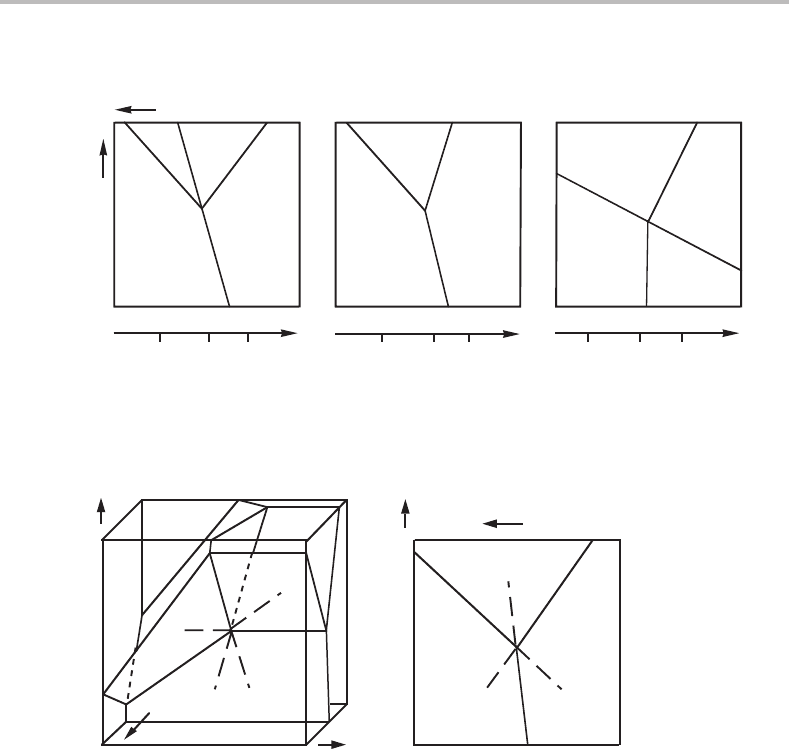
positions of the phases for the various cases of coincidence are shown in Fig. 10.12.

Other cases of coincidence may occur but not until at least one of these has occurred.

Before any rotation, the phases must have been arranged along the z

axis as shown in

Fig. 10.10 or in the completely reverse order.

216 Projected and mixed phase diagrams

(α)

(β)

(γ)

(δ)

αδβ,γ

α γ,δ β α,δ γ β

(a) (b) (c)

Figure 10.12 Three cases of coincidence of three-phase lines in a projected potential phase

diagram obtained by modifying Fig. 10.8.

(γ)

(β)

(δ)

(a) (b)

Figure 10.13 (a) Modiﬁcation of Fig. 10.8 by rotation of the entire diagram until the

β + γ + δ(α)isparallel to the µ

axis. All three surfaces, β + γ, γ + δ and δ + β, are then

parallel to the µ

axis. In the µ

projection (b), β + γ + δ(α)degenerates to a point and will

thus coincide with all the other lines without them coinciding with one another.

It is interesting to note from Fig. 10.8 that it should be possible to rotate the α + β

surface in such a way that the (γ) and (δ) lines approach each other and ﬁnally coincide.

However, the 180

◦

rule prevents this from happening before there is another coincidence.

What happens if three of the four phases β, γ and δ,have the same z

value will

now be investigated. The three surfaces representing β + γ, β + δ, γ + δ must all be

parallel to the µ

axis and the β + γ + δ(α) line must point in the µ

direction. It thus

degenerates to a point. This case is illustrated in Fig. 10.13.

Exercise 10.6

Prove mathematically that the compositions of β and γ must coincide when the µ

axis

in a binary system is parallel to the β + γ surface, as in Fig. 10.11.

10.5 Projection of higher-order invariant equilibria 217

Hint

Apply Eq. (8.47)tothe binary case.

Solution

Forabinary system we get (z

− z

)dµ

=−(S

− S

)dT +(V

− V

)dP. When

the β + γ surface is parallel to µ

, then we can change µ

and stay on the surface

without changing T or P, i.e. with dT = 0 and dP = 0. The coefﬁcient of dµ

must

thus be zero, i.e. z

= z

Exercise 10.7

Suppose one has measured µ

as function of T at 1 bar for a ternary A–B–C system.

What conclusion could be drawn if the diagram looks like Fig. 10.11(b) with µ

inserted

instead of P?

Hint

Compared to Fig. 10.11 we have one component more but the dimensionality has been

reduced to the same by keeping P constant. In both cases µ

and µ

are the potentials

that are not shown in the projection, i.e. those used to reduce the number of axes by

projection from the four-dimensional fundamental property diagram.

Solution

One of µ

and µ

is the dependent variable and the ﬁnal projection has been made in the

direction of the other one. From the coincidence of the (α) and (δ) lines we may conclude

that z

= z

if µ

is the dependent variable and z

= z

if µ

is the dependent one.

These two results are identical since z

= N

= 1/z

10.5 Projection of higher-order invariant equilibria

The topological examination may be extended to higher-order invariant equilibria and

adjoining univariant equilibria, although the visibility is then lost. However, it has been

shown by analytical methods [17–19] that the same principles, which have been derived

here by inspection, apply. Three components will yield a four-dimensional phase diagram

and it must be projected twice in order to yield a two-dimensional picture. It may show an

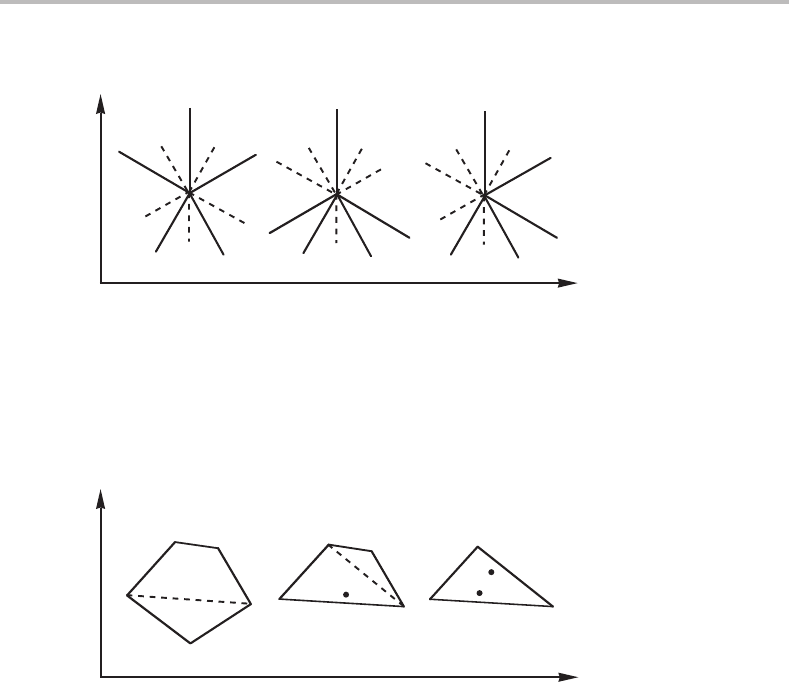
invariant ﬁve-phase equilibrium and ﬁve adjoining four-phase lines. If no lines coincide,

they can arrange themselves in three different ways, as illustrated in Fig. 10.14.

Foracloser discussion of the compositions of the phases taking part in the ﬁve-

phase equilibrium, the two potentials on the axes will be kept constant at the values of

the invariant equilibrium, while the two projected potentials will be replaced by their

218 Projected and mixed phase diagrams

(α) (α) (α)

(β)

(γ)

(δ)

(ε)

(a) (b) (c)

Figure 10.14 Possible Schreinemakers’ projections for a ternary system obtained by projecting the

, Y

phase diagram in the Y

and Y

directions. Points represent invariant ﬁve-phase

equilibria. The ﬁve lines radiating from each point represent four-phase equilibria and are

identiﬁed by giving the absent phase in parentheses. Dashed lines are metastable extrapolations.

αα

(a) (b) (c)

Figure 10.15 Molar phase diagrams at constant Y

and Y

showing the relative positions of the

ﬁve phases in the invariant equilibria in Fig. 10.14. The change occurring when lines (ε) and (β)

in case (a) are rotated to approach each other can be illustrated by moving point α towards the

straight line between δ and γ. Case (b) is obtained by letting the (ε) and (β) lines pass one

another, thus making point α cross the δ − γ tie-line. Case (c) is obtained by letting the (α) and

(δ) lines rotate and pass one another, whereupon ε will cross the β − γ line.

conjugate molar quantities. The ﬁve phases will fall on different points on the plane

formed by the two molar quantities, and Fig. 10.15 illustrates the arrangement of the

phases in the three different cases. Three phases may here be regarded as neighbours

if their points can be connected to form a triangle with no other point inside and if the

triangle can be changed into a line without any one of its points ﬁrst moving inside any

other such triangle. If two lines in the projected potential phase diagram coincide, then

the three phases they have in common will fall on a straight line in the molar diagram.

Four components yield a ﬁve-dimensional phase diagram and it must be projected

three times in order to yield a two-dimensional picture. A six-phase equilibrium will

be invariant and represented by a point from which six lines will radiate, representing

univariant equilibria with one phase absent in each. The relative positions of the six lines

will reveal how the six phases are arranged in the three-dimensional compositional space

formed by three molar quantities. However, this is not easy to visualize. The rule relating

10.5 Projection of higher-order invariant equilibria 219

(L)

(w)

(met)

logP

(gas)

(fay)

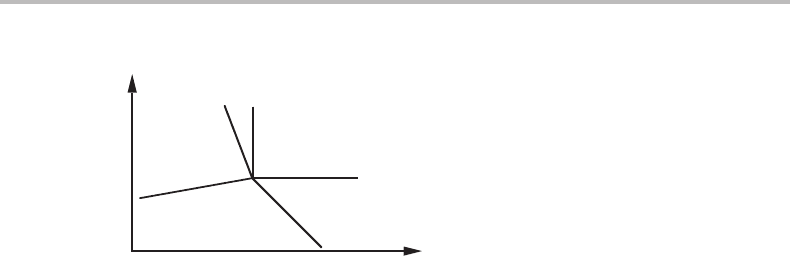
Figure 10.16 See Exercise 10.8.

the coincidence of lines in a projected potential phase diagram to the positions of the com-

mon phases in the space formed by the molar quantities has been called the ‘coincidence

theorem’ [19]. The theorem can be generalized as demonstrated by the following exam-

ple. Suppose that two of the points, α and δ,inthe left-hand picture of Fig. 10.15 coincide.

Then δ, α and γ fall on a line, and lines (β) and (ε)inFig.10.14 should coincide. However,

β, δ and α would also fall on a line, and lines (γ) and (ε)inFig. 10.14 should also coin-

cide. As a consequence all three lines, (β), (γ) and (ε), should coincide. It is thus possible

to generalize the coincidence theorem as follows. Consider a two-dimensional projection

of an r-dimensional potential diagram. It may have an invariant equilibrium involving

r + 1 phases. From this point, r + 1 univariant equilibria, each with r phases, radiate. The

theorem concerns the positions of the phases in the (r − 2)-dimensional space formed

by the molar quantities conjugate to the projected potentials. If t of the phases fall in a

(t − 2)-dimensional section through that space, then all the univariant equilibria, which

contain the t phases, coincide in the two-dimensional projection. There would be

r + 1 − t such equilibria.

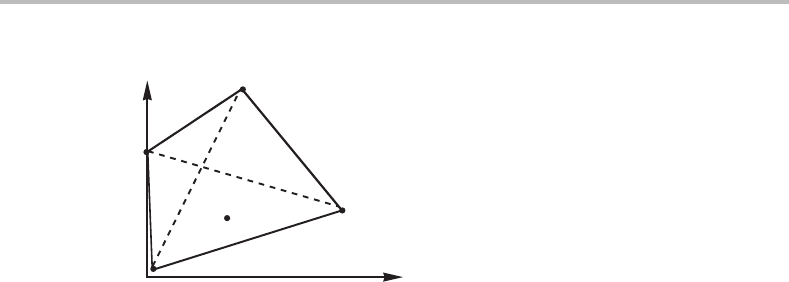
Exercise 10.8

Figure 10.16 is part of the potential phase diagram for the Fe–Si–O system, showing the

ﬁve-phase equilibrium, metallic melt (met), liquid melt (L), w¨ustite (w), fayalite (fay)

and gas (gas). Use the information in the diagram to decide how the composition of L

falls relative to the other phases.

Hint

By extrapolating the lines we ﬁnd that our case corresponds to case (b) in Fig. 10.14 with

L identiﬁed as α. Our diagram can be regarded as obtained by projecting the fundamental

potential diagram in the directions of P, µ

and µ

, leaving T and µ

as axes in our

diagram. The ﬁrst projection produces a complete potential phase diagram and, since

we are interested in comparing compositions, we shall regard P as subjected to the

ﬁrst projection. We should thus write the Gibbs–Duhem relation as dP = (S/ V )dT +

(N

/V )dµ

. The conjugate variable to the next two potentials to be projected would

thus be N

/V and N

/V . They should appear in our diagram as in Fig. 10.15(b).

220 Projected and mixed phase diagrams

met

fay

gas

Figure 10.17 Solution to Exercise 10.8.

Solution

Since L is identiﬁed as α,itwill have to form within the quadrangle formed by the other

four phases. Fayalite is 2FeO · SiO

,w¨ustite is approximately FeO and the metallic melt

is mainly Fe. The gas has a very large volume and will thus fall close to the origin in the

diagram. Since the extension of the (L) line in our potential phase diagram falls between

(gas) and (fay), corresponding to (γ) and (δ), its composition falls close to the gas +fay

join, corresponding to γ + δ join, as illustrated in Fig. 10.17.

10.6 The phase ﬁeld rule and mixed diagrams

The number of axes in a complete phase diagram, whether a potential one or a molar

one, is r = c + 1. For a closed system one has ﬁxed the composition and has actually

sectioned at c −1 molar axes. The number of remaining axes is r = c + 1 − (c − 1) = 2.

Foraclosed system the equilibrium state is thus uniquely deﬁned by choosing values

for T and P or their conjugate variables independent of how many phases it has. This is

called Duhem’s theorem.

In the most common type of phase diagram there is a temperature axis and a com-

position axis. It is thus an example of phase diagrams with a mixture of potential and

molar axes. Such diagrams are more complicated and due to the large variety no general

description will be given. However, it is worth discussing how the phase ﬁeld rule can

be generalized to such diagrams but ﬁrst it should be emphasized that the discussion

only concerns true phase diagrams, i.e. diagrams obtained from a single set of conjugate

pairs of variables. The nine possibilities were discussed in Section 3.5 and they resulted

in 27 sets when molar variables were introduced in Section 9.2.Asaconsequence, all

the variables in a mixed diagram, including those that have been projected or sectioned,

must come from one of the 27 sets in Tables 9.1, 9.2 and 9.3.

Figures 8.1 and 8.2 give the impression that the degrees of freedom increase by

one unit for each molar axis that is introduced instead of its conjugate potential axis.

However, it should be remembered that Gibbs’ phase rule was derived by considering

potentials and not molar quantities. The freedom to vary the amounts of the phases by

moving along a tie-line without varying the compositions of the individual phases is

10.6 The phase ﬁeld rule and mixed diagrams 221

not regarded as a degree of freedom in Gibbs’ phase rule because the potentials do not

vary. Instead of redeﬁning Gibbs’ phase rule we have thus decided to also to work with

a parallel concept, the dimensionality of a phase ﬁeld. That was the main reason why the

phase ﬁeld rule was introduced in Section 8.5. The effect of molar axes on Eq. (8.23)

yields

d = υ − n

+ n

= c + 2 − p − n

+ n

, (10.5)

where n

is the total number of sectioned quantities, potentials as well as molar quantities,

and n

is the total number of molar quantities used, i.e. sectioned molar quantities, n

as well as molar axes in the ﬁnal diagram, n

.Ofcourse, n

= n

+ n

.Onthe other

hand, if we project a phase diagram in the direction of an axis, then it does not matter

what kind of variable was chosen on that axis, a potential or its conjugate molar quantity.

The projected phase diagram will look the same and all the projections will thus have

the same effect on the phase ﬁeld rule. The number of projected molar quantities should

not be included in n

As before, the number of axes in the phase diagram will be given by Eq. (10.2),

r = c + 1 − n

− n

, and Eq. (10.5) can thus be written as

d = c + 2 − p − n

+ n

= 1 + r − p + n

+ n

for p ≥ 1 + n

+ n

. (10.6)

This expression is valid only as long as p ≥ 1 + n

+ n

because it yields d = r for

p = 1 + n

+ n

. This is a critical value because when the number of projections or

molar axes is increased further Eq. (10.6)would yield d > r which is impossible. For

each one of further projections and molar axes both the phase ﬁeld and the diagram will

lose one dimension and retain the relation d = r.For less phases we obtain instead of

Eq. (10.4),

d = r = c + 1 − n

− n

for p ≤ 1 +n

+ n

. (10.7)

Afew more considerations of the properties of mixed diagrams should be added. The

lowest possible dimensionality of a phase ﬁeld will occur for the maximum number of

phases. In a potential phase diagram that dimensionality will be zero but it is evident

from the preceding discussion that it will increase by one unit for each molar axis and

the lowest possible dimensionality will thus be equal to the number of molar axes in the

ﬁnal diagram, n

, and this will occur at the maximum number of phases. By inserting

+ n

= n

we obtain

= d

min

= c + 2 − p

max

− n

+ n

= r + 1 − p

max

+ n

(10.8)

max

= c + 2 − n

+ n

= r + 1 + n

+ n

. (10.9)

The MPL boundary rule can be applied to mixed diagrams but only with caution. It

is important ﬁrst to distinguish between phase ﬁelds and phase boundaries. The rule

concerns two adjoining phase ﬁelds separated by a phase boundary. As an example, we

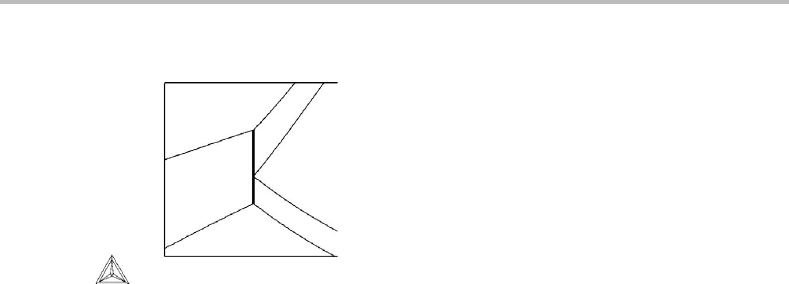
may examine the case illustrated in Fig. 9.2(c).Itisreproduced in Fig. 10.18 without

tie-lines and with the three-phase ﬁeld bcc + fcc + hcp marked with a thick line. All the

other lines are phase boundaries. The MPL rule cannot be applied to the contact between

222 Projected and mixed phase diagrams

500 1000

T (K)

⋅10

)

bcc

fcc

hcp

Figure 10.18 Mixed phase diagram from Fig. 9.2(c), reproduced without tie-lines. The thick line

represents the three-phase ﬁeld. All other lines are phase boundaries.

fcc and bcc + hcp phase ﬁelds because they are not connected by a phase boundary but

separated by the three-phase ﬁeld bcc +fcc +hcp. For the contact between fcc and bcc +

fcc + hcp the rule gives

b = r − D

− D

−

= 2 − 2 − 0 = 0,

in agreement with the fact that these two phase ﬁelds meet at a point, only. For the contact

between bcc + hcp and bcc + fcc the rule gives

b = r − D

− D

−

= 2 − 1 − 1 = 0.

This is also correct because these two phase ﬁelds do not make contact along the thick

horizontal line, where they are separated by the bcc + fcc + hcp phase ﬁeld. They

only make contact at the upper end-point of the thick line. Cases like this can be easily

analyzed by imagining that the one-dimensional phase ﬁeld is a very thin triangle [12].

That method is also helpful if one wants to draw zero-phase-fraction lines. Each one-

dimensional phase ﬁeld will have one such line on each side.

Exercise 10.9

The T,%Cphase diagram (Fig. 10.19) is for a quaternary A–B–C–D system at 20% B

and 20% D and at 1 bar. Test it with the phase ﬁeld rule.

Solution

There are four components, c = 4. The complete phase diagram has been sectioned

three times, n

= 3, but two of the sections were for the molar quantities %B and %D,

= 2. In the ﬁnal diagram there is one molar axis, n

= 1. There is no projection,

= 0. In the diagram we can see a horizontal line. Let us test if it is a phase ﬁeld or

just a boundary between two-dimensional phase ﬁelds. A line has the dimensionality

1 and it thus gives 1 = d = c + 2 − p − n

+ n

= 4 + 2 − p − 3 + 1 +2 =

6 − p; p = 5. If the horizontal line is a phase ﬁeld, it should have ﬁve phases. From

the neighbouring phase ﬁelds we ﬁnd α + β + γ + δ + L. We may conclude that this

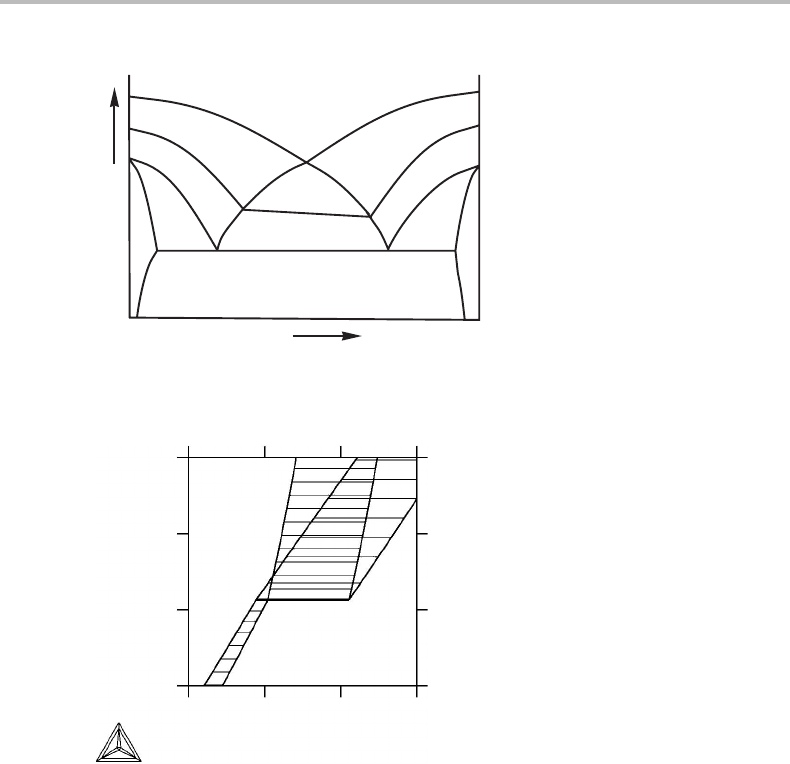
10.7 Selection of axes in mixed diagrams 223

α+β+γ+δ

L +β+γ+δ

L +α+β+δ

L+α

L+γ

L+γ+δ

L+ α+γ

L+α+δ

L+α+γ+δ

% C

Figure 10.19 See Exercise 10.9.

850

800

750

700

48 52

(J/molK)

56 60

bcc

T (K)

hcp

fcc

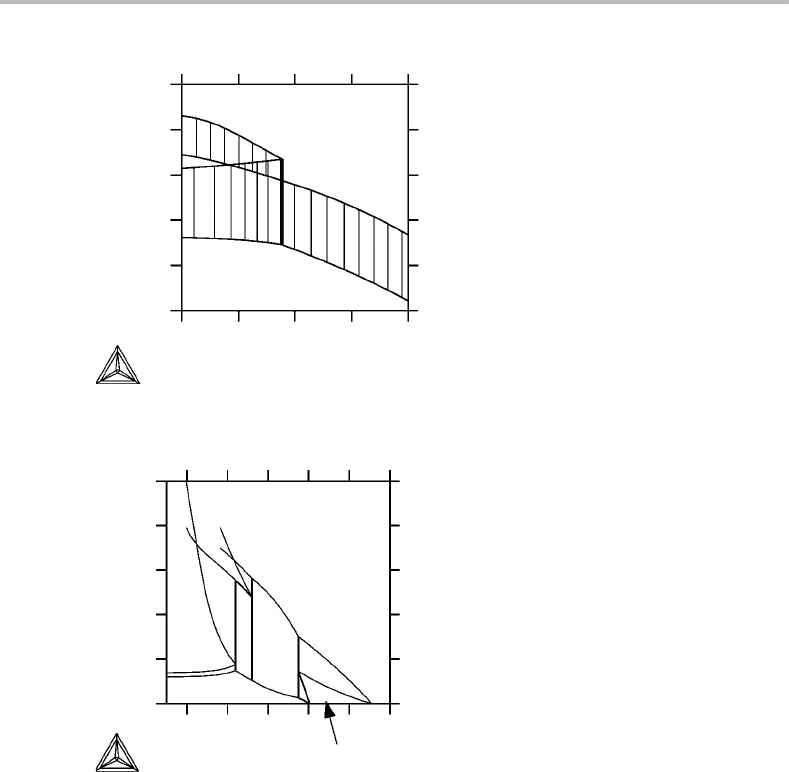
Figure 10.20 T , S

diagram for Fe. This is not a true phase diagram.

line is a phase ﬁeld. The diagram is two-dimensional, r = 2. Let us now check for

what number of phases a ﬁeld should be two-dimensional, p ≤ 1 + n

+ n

1 + 0 + 1 + 2 = 4. This is also conﬁrmed by the diagram.

10.7 Selection of axes in mixed diagrams

For mixed diagrams it is particularly important to pay attention to how the axes are

selected. As already emphasized, they must all come from a set of conjugate pairs

of variables and one from each conjugate pair. The various possibilities are listed in

Tables 9.1, 9.2 and 9.3.Anumber of examples will now be given in order to demonstrate

what could otherwise happen.

Figure 10.20 shows part of the T, S

diagram for Fe. Two two-phase ﬁelds overlap

which is made possible by the fact that T and S

do not represent different conjugate

pairs in any of the sets in the tables. This is not a true phase diagram.

224 Projected and mixed phase diagrams

100

−40 −35 −30 −25 −20

(kJ/mol)

liq

fcc

bct

(J/mol K)

Figure 10.21 S

,µ

diagram for Pb–Sn. This is not a true phase diagram.

1.0

0.8

0.6

0.4

0.2

−3 −2 −1010

bcc

fcc

cem

log(a

)

Figure 10.22 x

, a

diagram for Fe–Cr–C. This is not a true phase diagram.

Figure 10.21 shows the S

,µ

diagram for the Pb–Sn system at 1 bar. Two two-phase

ﬁelds overlap because S

and µ

do not come from the same set of conjugate pairs.

This is not a true phase diagram. One should have combined S

with µ

− µ

or S

with µ

Figure 10.22 shows the x

, a

diagram for Fe–Cr–C at 1 bar and 1200 K. The inter-

secting phase boundaries in the upper left corner, forming two ‘swallow-tails’, indicate

that this is not a true phase diagram. The activity a

can be regarded as an expression

for µ

/T and should have been combined with u

or z

but not x

Figure 10.23 shows the T, x

diagram for Fe–Cr–C at 1 bar and a

= 0.3, relative to

graphite. The two intersecting phase boundaries on the right-hand side indicate that this is

not a true phase diagram. The two axes, T and x

,dobelong to the same set of conjugate

variables but one must also consider the sectioned axes. In this case one has sectioned

at constant P and a

, i.e. µ

/T .However, µ

/T and x

do not belong to the same set.

Figure 10.24(a) shows the H

, a

diagram for Fe–C at 1 bar. This is not a true phase

diagram although H

and µ

/T, here represented by a

, come from the same set of