Hillert M. Phase Equilibria, Phase Diagrams and Phase Transformations: Their Thermodynamic Basis

Подождите немного. Документ загружается.

9.4 Sections of molar phase diagrams 195

Solution

This is a three-dimensional diagram, r = 3, and the dimensionality of the α − β line

is one, b = 1. We get D

−

= r − b = 3 − 1 = 2. The number of phases has decreased

from 4 to 2. We have moved into the α + β two-phase region by crossing the α − β line.

The dimensionality of the β point is zero, b = 0, and we get D

−

= r − b = 3 − 0 = 3.

The number of phases has decreased from 4 to 1. We have moved into the β one-phase

region by crossing the β point.

9.4 Sections of molar phase diagrams

A diagram with a full set of molar axes may be called a complete molar phase diagram.

For practical reasons one often likes to reduce the number of axes. A popular method is

to section at a constant value of a potential, e.g. P or T. The resulting diagram looks just

like a complete molar phase diagram for a system with one component less. Another

method is to section at a constant value of a molar variable, a so-called isoplethal section

or an isopleth.

Since all phase ﬁelds in a molar phase diagram have the same dimensionality as

the phase diagram has axes, all kinds of phase ﬁelds may show up in that kind of

section whereas a phase ﬁeld with the maximum number of phases (i.e. for an invariant

equilibrium) will disappear in an equipotential section because the section cannot be

expected to go exactly through a given point. The topology of a molar section is simpliﬁed

if it is again accepted that it will not be possible to place a section exactly through a point.

All two-dimensional sections with molar axes will be composed of the elementary unit

shown in Fig. 9.8 and all three-dimensional sections will be composed of the elementary

unit shown in Fig. 9.9, independent of how many potential or molar axes have been

sectioned. Of course, if one adds a component, one must section once more in order

to keep the number of dimensions. As an example, two sections through Fig. 9.4 are

indicated in Fig. 9.10.Ineach case, the section gives the same arrangement of lines as in

Fig. 9.8(a). Furthermore, the MPL boundary rule applies to the sections, since the value

of r – b does not change by sectioning.

Inspection of the two sections in Fig. 9.10 reveals that one shows an intersection

between phase ﬁelds of 2, 3, 3 and 4 phases and the other 1, 2, 2 and 3 phases. We may

thus give the general picture shown in Fig. 9.11.For the sections shown in Fig. 9.10 we

have e = 3 and 4, respectively, where e is the highest number of phases in any of the two

adjoining phase ﬁelds. In fact, the maximum value of e in a two-dimensional diagram,

which is also the maximum number of phases in a phase ﬁeld, depends upon the number

of sectioned molar axes, n

max

= 3 + n

. (9.12)

Exercise 9.5

On the right-hand side of the tetrahedron in Fig. 9.10 there is a triangular prism. Make

a section through that prism parallel to the side of the tetrahedron. Make a sketch of the

196 Molar phase diagrams

Figure 9.10 Two sections through the molar phase diagram of Fig. 9.4. The sections are shown

with thin lines.

e–2

e–1 e–1

e–2

Figure 9.11 Elementary unit of a molar phase diagram, sectioned a sufﬁcient number of times to

make it two-dimensional. The diagram may have units with different e values from 3 up to a

maximum, determined by the number of sectionings.

intersection obtained at the front edge of the prism. Indicate the number of phases in the

four adjoining phase ﬁelds.

Hint

It may be useful to go back to the Exercise 9.4.

Solution

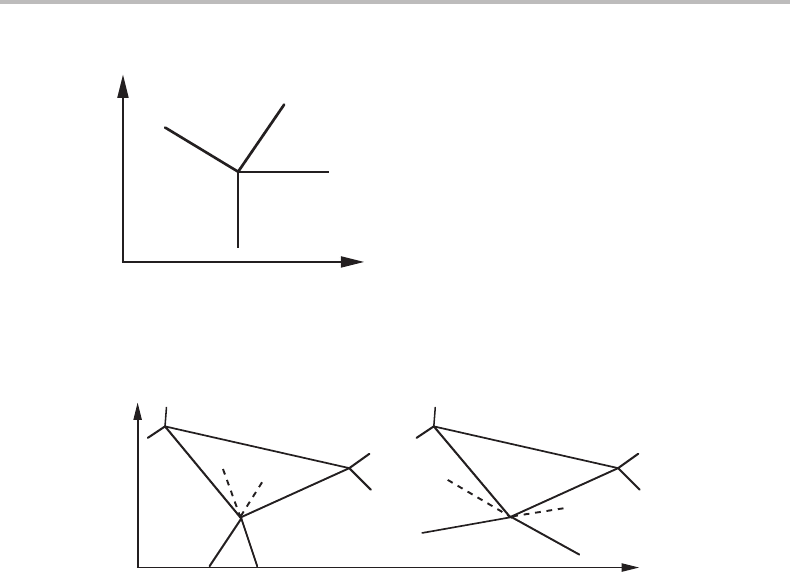
The solution is given in Fig. 9.12.

9.5 Schreinemakers’ rule 197

Figure 9.12 Solution to Exercise 9.5.

α+β

α+β+γ

β+γ

α+γ

α+β

α+γ

β+γ

α+β+γ

(a) (b)

Figure 9.13 Elementary unit of a phase diagram with two molar axes. Two of the phase

boundaries of the one-phase ﬁeld are shown.

9.5 Schreinemakers’ rule

When studying isobarothermal sections of ternary diagrams Schreinemakers [13] found

that the extrapolations of the boundaries of the one-phase ﬁeld in the elementary unit

must either both fall inside the three-phase ﬁelds or one inside each of the two two-

phase ﬁelds. This is illustrated in Fig. 9.13 and is called Schreinemakers’ rule. It can be

generalized in the following way [14].

Let us examine if Schreinemakers’ rule applies to different e values and start by

considering a complete phase diagram constructed with molar axes only. A discussion of

thermodynamic properties should then be based upon the internal energy. For reversible

changes we obtain

dU = T dS − PdV +



. (9.13)

In Section 4.6 we saw that it is always possible to introduce a new set of components

instead of the old one by combining the components in a new way as long as we get

a complete set of independent components and do not change the value of the sum,

µ

.Wecan do so by selecting c points in the compositional space and make sure

that they can be used to deﬁne a new set of independent components by checking that

three of them never fall on a line, four of them never fall on a plane, etc. We shall use this

method of changing to a new set of components but we shall then consider entropy and

198 Molar phase diagrams

α+k + j

(a) (b)

Figure 9.14 General proof of Schreinemakers’ rule.

volume as components, whose amounts are expressed by S and V, and whose chemical

potentials are T and −P, respectively. The introduction of c + 2new components instead

of the old ones will now be effected by selecting c + 2 points in the state diagram. They

will each be identiﬁed by an index d.

We can follow the procedure outlined in Section 4.6 and obtain

dU =

c+2



c+2



, (9.14)

where µ



and N



.For these generalized chemical potentials,

the following Maxwell relation is obtained



∂µ

∂ N



∂

∂ N



∂µ

∂ N



. (9.15)

When considering the cases in Fig. 9.13 with a tie-triangle in the section, we shall include

the β and γ corners in the set of new components. In a more general case we shall denote

them by k and j (see Fig. 9.14).

At the point under consideration, one of the two boundaries, the extrapolations of

which we discuss, represents equilibrium with k, and is thus an equipotential line for k

in α.Ifitextrapolates outside the α − k − j triangle, the potential of k must increase on

moving closer to the point j, because this path intersects equipotential lines for k in α

situated closer to the point k, i.e.

∂µ

∂ N

> 0 (9.16)

(see thin line in Fig. 9.14(b)). Then, from the Maxwell relation,

∂µ

∂ N

> 0 (9.17)

It follows that the second boundary must also extrapolate outside the α − k − j triangle.

On the other hand, if the k boundary extrapolates into the triangle, a movement towards

the point j will intersect equipotential lines for k further away from the point k (see thin

line in Fig. 9.14(a)). Both derivatives must then be negative, and both boundaries must

9.5 Schreinemakers’ rule 199

1500

1400

1300

T (K)

1200

1100

1000

0 0.5 1.0

mass-% C

1.5 2.0

Figure 9.15 Calculated phase diagram for system with seven components. The complete phase

diagram has two potential axes and six molar axes and has been sectioned at one constant

potential, P, and ﬁve constant molar quantities, x

. Schreinemakers’ rule holds at all

intersections. Numbers given are number of phases in each phase ﬁeld.

extrapolate into the triangle. It has thus been shown that the extrapolations of both phase

boundaries under consideration must fall either outside the highest-order phase ﬁeld or

inside it, in agreement with Schreinemakers’ rule. It may be emphasized that the rule also

holds for equipotential sections. In order to prove it in such a case, one must use a Maxwell

relation based on a thermodynamic function which allows the corresponding potentials

to be kept constant, for instance G in the case actually considered by Schreinemakers,

constant T and P.

In the derivation of Schreinemakers’ rule it is essential that the two boundaries of

the highest-order phase ﬁeld of those considered are straight lines. That this happens

in the ternary case under isobarothermal conditions is self-evident because then the tie-

triangle is situated in the plane of the diagram. In a quaternary system the sides of a

four-phase equilibrium will be planar and the intersections shown in a two-dimensional

section will be straight lines. The components k and j then represent two-phase mixtures

situated in the section. On the other hand, a three-phase equilibrium will not be bounded

by planar sides and its boundaries in the two-dimensional section will not be straight

lines. Then the boundaries of the one-phase ﬁeld will not be equipotential lines for any

components k and j chosen in the section. It may be concluded that the proof, given above,

is not rigorous except when an equilibrium of the highest order allowed in the section

is involved. However, experience shows that Schreinemakers’ rule is obeyed in most

cases, and it may be used as a convenient guide when other information is lacking. As

an example, the result of a computer-operated calculation of a section through a seven-

component system is presented in Fig. 9.15. The rule is satisﬁed at all the intersections

in this diagram.

Figure 9.16 shows an apparent violation of Schreinemakers’ rule at the corner of the

bct phase ﬁeld. However, this is not a true phase diagram because S

and z

never appear

in the same set of conjugate variables in Table 9.2.

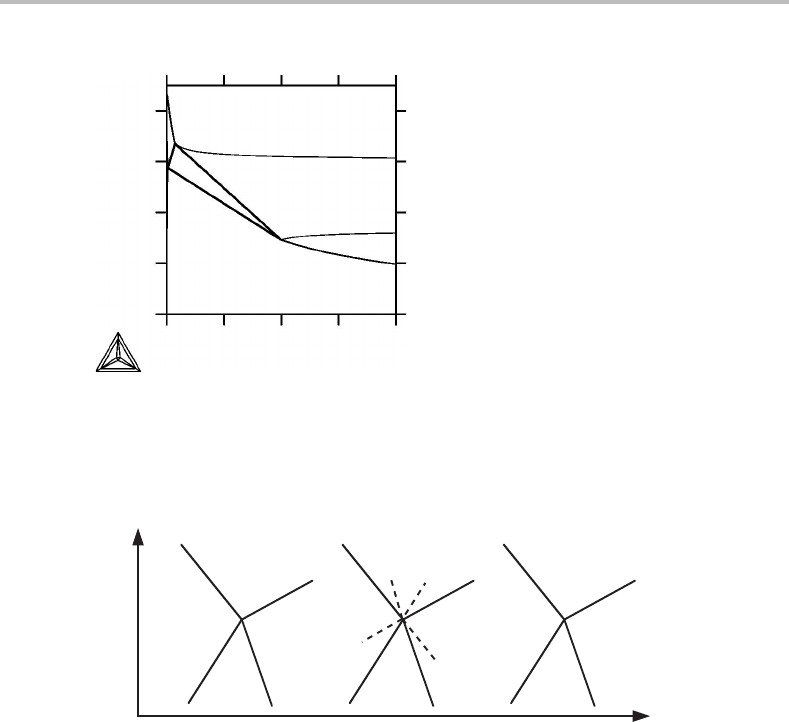
200 Molar phase diagrams

020

(J/molK)

fcc+bct

lip+bct

lip

bct

60 80

Figure 9.16 S

, z

diagram for Pb–Sn at 1 bar. It shows an apparent violation of

Schreinemakers’ rule but is not a true phase diagram.

e –1

e –2

e –1

(a) (b) (c)

Figure 9.17 Use of Schreinemakers’ rule to decide which phase ﬁelds have equal number of

phases.

Usually, Schreinemakers’ rule is used to predict the directions of phase boundaries.

On the other hand, if the phase boundaries are given, for instance from calculation or

experiment, then the rule can help to give the number of phases in the various phase

ﬁelds. Suppose the arrangement in Fig. 9.17(a) is given, but the numbers of phases in

the four adjoining phase ﬁelds are not known. One should then extrapolate all the lines,

as shown in Fig. 9.17(b).Two of the phase ﬁelds will contain one extrapolation each,

and these phase ﬁelds will be opposite to one another. According to Schreinemakers’

rule, these will be the phase ﬁelds with the same number of phases, e −1inFig.9.17(c).

Of the two remaining phase ﬁelds, one will contain two extrapolations and the other

none. These phase ﬁelds will contain one phase more and one phase less than the others,

respectively. However, the rule does not allow us to tell which has more and which less.

It would be possible to predict the number of phases in all the phase ﬁelds of Fig. 9.15

by this method, if it were known that the phase ﬁeld in the upper left corner has one

phase.

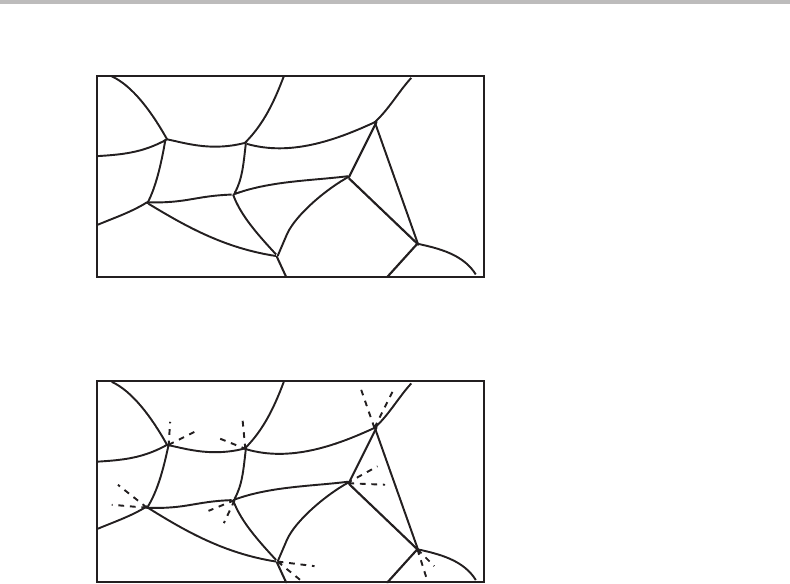
9.6 Topology of sectioned molar diagrams 201

Figure 9.18 See Exercise 9.6.

Figure 9.19 Solution to Exercise 9.6.

Exercise 9.6

A diagram for a multicomponent system is given in Fig. 9.18 but the numbers of phases

have been left out except for one phase ﬁeld. Try to decide the numbers of phases in all

the other phase ﬁelds.

Hint

Discuss ﬁrst what kind of phase diagram it is.

Solution

It looks like a molar diagram because at each point of intersection there are four lines.

It may thus be reasonable to use Schreinemakers’ rule. The result is shown in Fig. 9.19.

9.6 Topology of sectioned molar diagrams

Before leaving the discussion of sections of molar phase diagrams we should further

consider the topology of diagrams with several phases. Figure 9.8 showed the elementary

unit of a two-dimensional molar diagram. The result of sectioning can vary depending

upon the direction of sectioning and the regularity of the diagram before sectioning.

However, topologically the whole section can be regarded as composed of intersecting

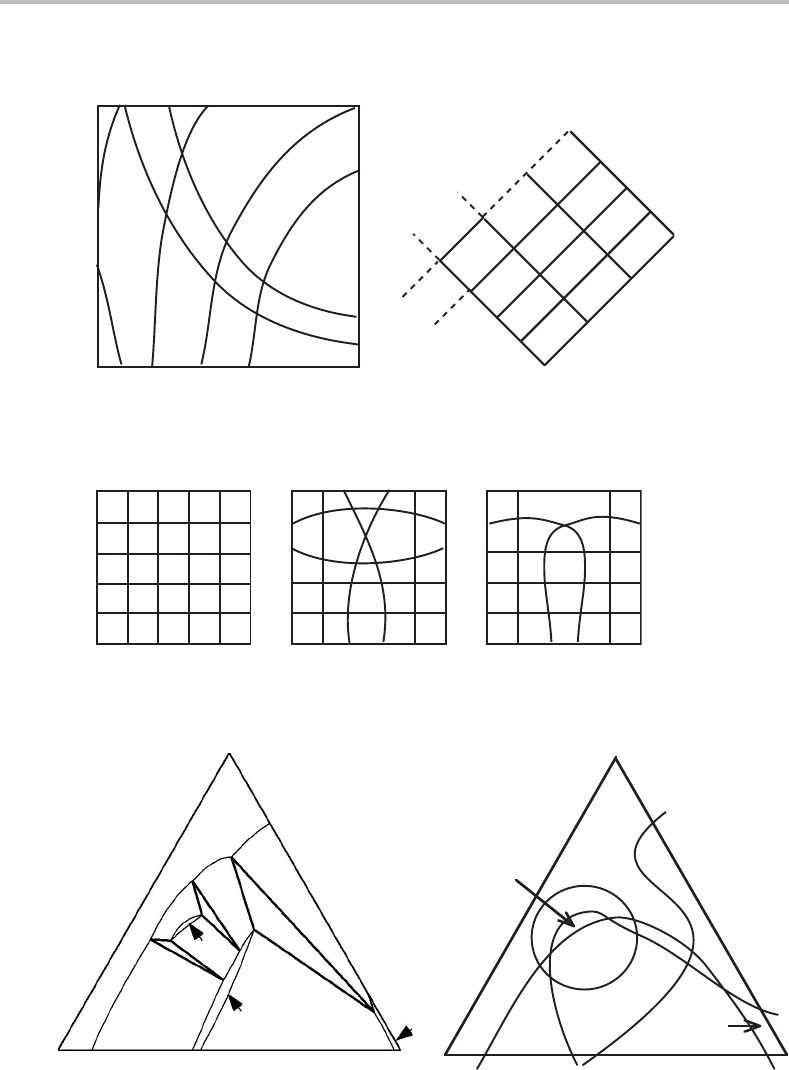
202 Molar phase diagrams

(a) (b)

Figure 9.20 Two diagrams topologically equivalent to the sectioned molar phase diagram of

Fig. 9.15.

(a) (b) (c)

111111

222

223

334 4

Figure 9.21 Some possibilities for the topology of a sectioned molar phase diagram with several

phases. Both axes are molar axes.

Fe W

Cr(a)

(b)

Figure 9.22 (a) The Fe–W–Cr phase diagram at 1 bar and 1673 K. α and β are both bcc but do

not mix completely. µ and σ are intermetallic phases. (b) Topologically equivalent diagram but

drawn with lines without any sharp points. These lines represent the limit of existence for one

phase each, as given by the letters outside the triangle. The circle is the limit for σ.

9.6 Topology of sectioned molar diagrams 203

γ+δ+ε

α+γ+δ+ε

α+δ+ε

γ+δ+ε

δ+ε

β+δ+ε

β+ε

α+β+ε

α+δ+ε α+ε

α+ε α+β+ε

α+γ+ε

β+ε

γ+δ+ε

δ+ε

γ+δ+ε

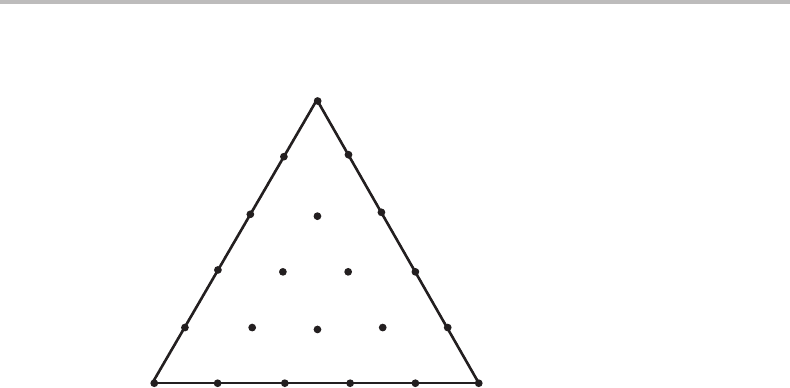
Figure 9.23 See Exercise 9.7.

lines, and the elementary unit will be the same as in Fig. 9.8(b).Bythe same reasoning,

a three-dimensional diagram will have elementary units like the one in Fig. 9.9 and will

give units like the one in Fig. 9.8(b) after sectioning. A many-dimensional molar phase

diagram, after being sectioned a sufﬁcient number of times, may look something like the

one illustrated in Fig. 9.20(a).Itwas constructed to be topologically equivalent to the

phase diagram in Fig. 9.15.InFig. 9.20(b) it has been further simpliﬁed but it still has

the same topology. This is an unusually simple case. The lines may very well intersect

in a more complicated manner, as illustrated in Fig. 9.21.

The observation by Masing can be generalized. For each one of the lines in a two-

dimensional section of a molar phase diagram there is a phase which ceases to exist

on the line. It is illustrated for a complicated case in Fig. 9.22(a), using the topo-

logically equivalent diagram in Fig. 9.22(b). These lines running through a compli-

cated phase diagram have been called ‘zero-phase-fraction’ lines by Gupta, Morral

and Nowotny [15] and they can be used as a valuable tool for identifying the phase

ﬁelds and even for constructing a phase diagram from experimental information. The

same principle applies to the surfaces in three-dimensional sections of molar phase

diagrams.

Exercise 9.7

In order to investigate the phase relations in a quinary system Gupta, Morral and Nowotny

established equilibrium in 21 alloys by isothermal treatment at 1400 K and 1 bar. All

alloys had the same molar content of two components. The phases found in the various

alloys could thus be shown in a composition triangle (see Fig. 9.23,where the composi-

tions are represented by the relative fractions of the three remaining components). Draw

a reasonable phase diagram.

204 Molar phase diagrams

(a) (b)

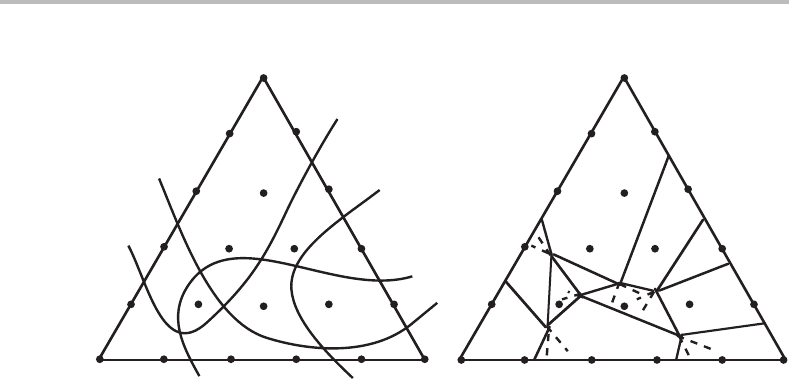
Figure 9.24 Solution to Exercise 9.7.

Hint

The diagram is a molar phase diagram. Start by drawing lines showing the limit of

existence of each phase (zero-phase-fraction lines). Improve the diagram by making the

various phase boundaries reasonably straight. Phase boundaries for invariant equilibria

must be quite straight. Improve the diagram further by applying Schreinemakers’ rule.

Solution

At constant T and P the maximum number of phases in a quinary system is ﬁve. None

of the alloys falls in such a phase ﬁeld. All the phase boundaries may thus be curved but

we may ﬁnd that it is possible to use straight lines which is preferable when we do not

know in which direction a line should be curved. Figure 9.24 shows a possible solution.