Hillert M. Phase Equilibria, Phase Diagrams and Phase Transformations: Their Thermodynamic Basis
Подождите немного. Документ загружается.

8.7 Ternary systems 175
10
8
6
4
2
0
2.0
1000/T
log(P
CO
2
/P
CO
)
1.5 1.0 0.5
Cu
CuO
⋅ CuSO
4
CuSO
4
Cu
2
O
Cu
2
S
CuS
CuO
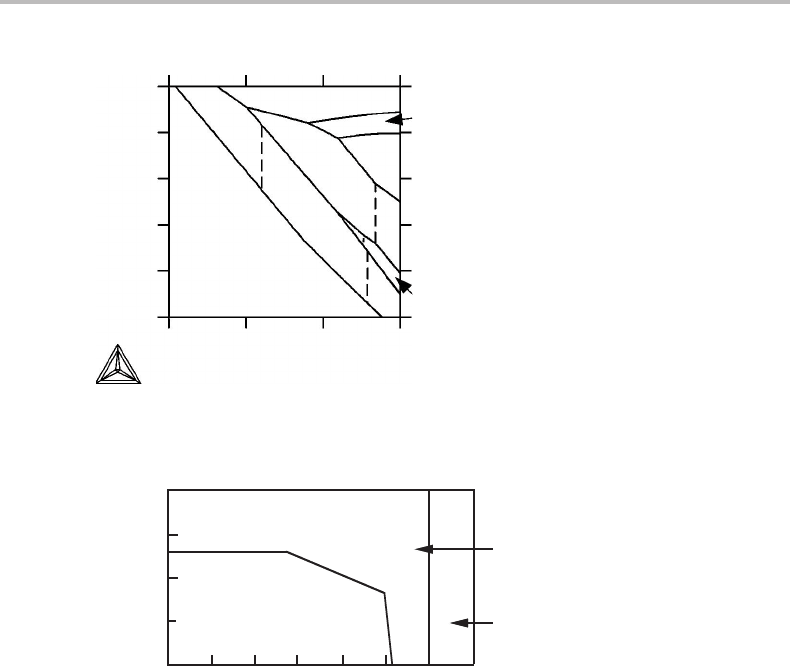
Figure 8.19 The Cu–O–S phase diagram sectioned at 1 bar and a potential of SO
2
equal to the
potential of pure SO
2
gas of1bar.
α
β
log P
O
2
log P
N
2
−27 −26 −25 −24 −23 −22 −21 −20
−3.7
−3.8
−3.9
Si
Si
2
N
2
O
SiO
2
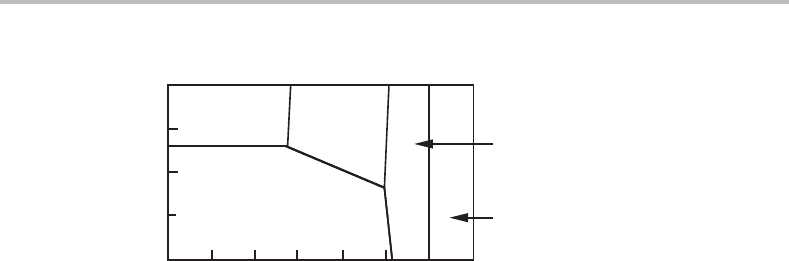
Figure 8.20 See Exercise 8.9.
where the logarithm of the contents of O and S in liquid iron are used for representing the
Ce–O–S phase diagram at constant temperature and pressure. With these axes one can
directly see what cerium compound should form first from liquid iron if the cerium con-
tent is gradually increased. However, the diagram does not reveal what cerium contents
are required in the liquid iron phase.
One may also section a ternary phase diagram at some value of a chemical potential
and keep the temperature as an axis. Figure 8.19 shows such a case sectioned at a constant
value of µ
S
+ 2µ
O
and plotted with µ
O
/RT versus 1/T. Here µ
O
/RT is expressed by the
ratio of the partial pressures of CO
2
and CO in an ideal gas.
Exercise 8.9
Figure 8.20 shows at what O
2
and N
2
pressures three nitrides can form from pure Si at
1840 K. (a) Use the slopes in order to evaluate the O content in α and β, both of which
are usually considered to be Si
3
N
4
. (b) Their coexistence lines are missing in the phase
diagram. Calculate their slopes.
176 Phase equilibria and potential phase diagrams
α
β
log P
O
2
log P
N
2
−27 −26 −25 −24 −23 −22 −21 −20
−3.7
−3.8
−3.9
Si
Si
2
N
2
O
SiO
2
Figure 8.21 Solution to Exercise 8.9.
Hint
The axes may be regarded as potential axes for O and N because T is constant. We can
thus apply the relation dµ
O
/dµ
N
=−(z
γ
N
− z
δ
N
)/(z
γ
O
− z
δ
O
), similar to Eq. (8.34). The Si
phase does not dissolve noticeable amounts of O or N. In all the oxides and oxynitrides
we can assume the following valencies: +4 for Si, −2 for O, −3 for N.
Solution
(a) z
i
is here defined as N
i
/N
Si
.Forα/Si we read dµ
O
/dµ
N
=−45 =−(z
α
N
− 0)/
(z
α
O
− 0) =−z
α
N
/z
α
O
. Applying electroneutrality, 4 = 2z
α
O
+ 3z
α
N
= 2z
α
O
+ 45 ·
3z
α
O
= 137z
α
O
; z
α
O
= 0.0292; z
α
N
= 45 · 0.0292 = 1.3139. Figure 8.21 thus predicts
that the formula for the α phase is Si
1
N
1.3139
O
0.0292
or Si
2.978
Va
0.022
N
3.913
O
0.087
.
For β/Si we read dµ
O
/dµ
N
=∞=−(z
β
N
− 0)/(z
β
O
− 0); z
β
O
= 0. The formula
for β is Si
3
N
4
.
(b) For α/β we then get: dµ
O
/µ
N
=−(1.313 − 1.3333)/(0.0292 − 0) = 0.664. For
α/Si
2
N
2
Oweget: dµ
O
/µ
N
=−(1.3139 − 1)/(0.0292 − 0.5) = 0.667. The two
new coexistence lines will thus be parallel and almost vertical in Fig. 8.21 because
of the very enlarged scale for log P
N
2
.
Exercise 8.10
For the invariant equilibrium TiCl
4
+ TiO
2
+ Ti
3
O
5
in Fig. 8.17 it has been found that the
partial pressure of Ti is 5 × 10
−22
bar. Construct a reasonable log P
O
2
, log a
Ti
diagram
for these three phases at the constant values of T and P.
Hint
Evidently, the potential diagram in Fig. 8.17 was obtained from the fundamental property
diagram by first sectioning twice (at constant T and P) and then projecting in the µ
Ti
direction. Now we are asked instead to project in the µ
Cl
direction. Start by plotting the
point for the three-phase equilibrium at log P
Ti
=−21.3 and a value of log P
O
2
obtained
from Fig.8.17. Then we can calculate the slopes of invariant equilibria in terms of the

8.8 Direction of phase fields in potential phase diagrams 177
compositions involved. When one obtains an indeterminate value one should go back to
the derivation of the equation used.
Solution
At constant T, P we have a three-dimensional property diagram looking like Fig. 8.7(a)
but with µ
Ti
, µ
O
and µ
Cl
on the axes. Figure 8.17 is the projection on the µ
O
, µ
Cl
side.
Now we want the projection on the µ
O
, µ
Ti
side. Then we must project in the µ
Cl
direc-
tion and define z
i
as N
i
/N
Cl
.ForTiO
2
and Ti
3
O
5
we get z
O
and z
Ti
equal to infinity.
We should thus go back to the Gibbs–Duhem relation for two phases, α and β, and get
x
α
Ti
dµ
Ti
+ x
α
O
dµ
O
+ x
α
Cl
dµ
Cl
= 0 and x
β
Ti
dµ
Ti
+ x
β
O
dµ
O
+ x
β
Cl
dµ
Cl
= 0.
For TiO
2
/TiCl
4
: x
α
Cl
= 0 and already the first equation yields dµ
Ti
/dµ
O
=−x
α
O
/x
α
Ti
=
−2 and d ln a
Ti
/dlnP
O
2
= 0.5dµ
Ti
/dµ
O
=−1.
For Ti
3
O
5
/TiCl
4
: x
α
Cl
= 0 and already the first equation yields dµ
Ti
/dµ
O
=
−x
α
O
/x
α
Ti
=−5/3 and d ln a
Ti
/dlnP
O
2
= 0.5dµ
Ti
/dµ
O
=−5/6.
For TiO
2
/Ti
3
O
5
: x
α
Cl
= x
β
Cl
= 0 and the only solution to the two equations is dµ
Ti
= 0
and dµ
O
= 0. This two-phase equilibrium will thus occur in one point only (see Fig.
8.22). The reason is that we have projected the property diagram in the direction of the
TiO
2
+ Ti
3
O
5
coexistence line.
In a two-dimensional potential phase diagram we normally expect to see two-
dimensional phase fields for single phases and one-dimensional phase fields for two
phases in equilibrium. As expected, the phase field for TiCl
4
is two-dimensional but not
the one for TiO
2
or Ti
3
O
5
.However, since TiO
2
and Ti
3
O
5
do not dissolve any Cl, their
properties are not affected by µ
Cl
. The µ
Cl
axis in the fundamental property diagram is
thus parallel to the property surface of both phases and hence parallel to the line rep-
resenting their intersection. In the µ
Cl
projection these surfaces will become lines and
their intersection, representing a two-phase equilibrium, will become a point. Compare
Fig. 8.7 and let µ
Ti
correspond to µ
A
, let µ
O
correspond to −P and µ
Cl
correspond to T.
Rotate all the surfaces slightly until the β + γ coexistence line is parallel to the T axis.
It will then appear as a point in the T projection.
8.8 Direction of phase fields in potential phase diagrams
In the discussions of two-dimensional phase diagrams we have several times derived
equations for the slope of two-dimensional phase fields. We shall now give a more general
treatment. The direction of phase fields is governed by the Gibbs–Duhem relation, which
applies to each one of the p phases in an equilibrium, e.g. for the phase α:
− S
α
m
dT + V
α
m
dP −
x
α
i
dµ
i
= 0. (8.36)
If all the phases stay in equilibrium with each other when some variation is made, each of
dµ
i
,dT and dP must have the same value for all phases. By combining the Gibbs–Duhem
relation for all phases one obtains a system of equations for the coexistence of the phases
in the fundamental property diagram. With p phases we have p Gibbs–Duhem relations
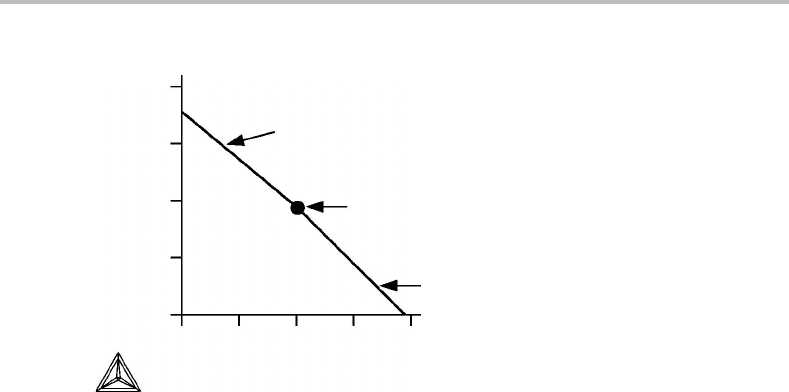
178 Phase equilibria and potential phase diagrams
0
−10
Ti
3
O
5
can only
exist on this line
TiCl
4
Ti
3
O
5
and TiO
2
can exist
together in this point only
TiO
2
can only
exist on this line
−20
−30
−40
−40 −30
log(P
O
2
)
log(P
Ti
)
−20 −10 0
Figure 8.22 Solution to Exercise 8.10.
and can thus eliminate p −1ofthe variables. If we would choose to eliminate µ
i
for i
from 1 to p −1, we should multiply each equation by a factor that we can represent by a
determinant. For example, the equation for the α phase should be multiplied by a factor
x
β
1
x
β
2
..x
β
p−1
x
γ
1
x
γ
2
..x
γ
p−1
.....
.....
x
ε
1
x
ε
2
..x
ε
p−1
.
As a shorthand notation such a determinant will be written by giving the diagonal ele-
ments |x
β
1
x
γ
2
..x
ε
p−1
| .Byadding the equations for all the phases, we obtain
−
S
α
m
x
β
1
x
γ
2
..x
ε
p−1
|dT +|V
α
m
x
β
1
x
γ
2
..x
ε
p−1
dP −
x
α
i
x
β
1
x
γ
2
..x
ε
p−1
dµ
i
= 0.
(8.37)
Using an alternative form of the Gibbs–Duhem relation found from line 5 in Table 3.1
we instead obtain
H
α
m
x
β
1
x
γ
2
..x
ε
p−1
|
d(1/T )+
|
V
α
m
T
x
β
1
x
γ
2
..x
ε
p−1
dP
−
x
α
i
x
β
1
x
γ
2
..x
ε
p−1
d(µ
i
/T ) = 0. (8.38)
The factors in front of dµ
i
or d(µ
i
/T) for i from 1 to p − 1 are zero because two
columns have the same elements. For instance, with i = p − 1 the first and last columns
in the last determinant are identical. It should be emphasized that the equation can be
formulated in many ways by including different µ
i
in the set of eliminated variables. All
such alternative equations apply simultaneously and together they give the direction of
the phase field. We shall now consider various cases by considering different values of
p − c and in some cases different values of p.

8.8 Direction of phase fields in potential phase diagrams 179
For p = c + 1 we have a univariant equilibrium according to Gibbs’ phase rule, υ = 1,
and shall thus obtain a linear phase field in the potential phase diagram. All the dµ
i
or
d(µ
i
/T) can be eliminated mathematically because c = p − 1. Furthermore, in this case
each column in each determinant contains all the x
i
in a phase and we can make use of
x
i
= 1inthe remaining terms,
H
α
m
1 x
γ
2
..x
ε
c
d(1/T ) +
V
α
m
1 x
γ
2
..x
ε
c
dP/T = 0. (8.39)
This gives the direction of the phase field in a (1/T), P phase diagram produced by
projection of the complete phase diagram. As an example, for a binary system with three
phases the equation gives
H
α
m
1 x
γ
2
d(1/T ) +
V
α
m
1 x
γ
2
dP/T = 0. (8.40)
This gives the slope of the phase field for a univariant phase equilibrium in a projection
onto the (1/T), P side of the phase diagram. It can also be written as follows,
dP
dT
=
x
γ
2
− x
β
2
H
α
m
+
x
α
2
− x
γ
2
H
β
m
+
x
β
2
− x
α
2
H
γ
m
x
γ
2
− x
β
2
V
α
m
+
x
α
2
− x
γ
2
V
β
m
+
x
β
2
− x
α
2
V
γ
m
·
1
T
. (8.41)
In Section 13.2 we shall see that the equation can be reduced to a much simpler form.
In fact, the numerator is equal to the heat of the three-phase reaction between α, β and
γ and is thus independent of the choice of reference states chosen for the H values. The
denominator is equal to the change in volume. Thus, the value of dP/dT is indepen-
dent of the choice of references, as it should be, and Eq. (8.41)isageneralization of
Eq. (8.17).
If we had eliminated d(µ
1
/T ) and dP instead of d(µ
1
/T ) and d(µ
2
/T )wewould have
obtained
d
(
µ
2
/T
)
d
(
1/T
)
=
V
γ
m
− V
β
m
H
α
m
+
V
α
m
− V
γ
m
H
β
m
+
V
β
m
− V
α
m
H
γ
m
V
γ
m
− V
β
m
x
α
2
+
V
α
m
− V
γ
m
x
β
2
+
V
β
m
− V
α
m
x
γ
2
. (8.42)
This is the slope of the phase field for a univariant phase equilibrium in a projection onto
the (µ
2
/T ), (1/T ) side of the complete phase diagram. The value of the numerator here
depends upon the choice of reference states for the H values and that choice will thus
affect the value of d(µ
2
/T )/d(1/T ).
For p = c we have a divariant equilibrium, υ = 2, and the corresponding phase field
will form a surface in the phase diagram. We can, for instance, eliminate all d(µ
i
/T) terms
except for d(µ
c
/T) and obtain a relation between d(1/T), dP and d(µ
c
/T), representing
the direction of the two-dimensional phase field in a three-dimensional projection of the
complete phase diagram:
H
α
m
x
β
1
x
γ
2
..x
ε
c−1
d(1/T ) +
V
α
m
/T
x
β
1
x
γ
2
..x
ε
c−1
dP
=
x
α
c
x
β
1
x
γ
2
..x
ε
c−1
d(µ
c
/T ). (8.43)

180 Phase equilibria and potential phase diagrams
Under isobaric conditions we obtain a one-dimensional phase field, the slope of which
is given by
x
α
1
x
β
2
..x
δ
c−1
H
ε
m
d(1/T ) =
x
α
1
x
β
2
..x
δ
c−1
x
ε
c
d(µ
c
/T ).
(8.44)
For p = c − 1 we obtain a similar equation but now two terms will remain of the
summations in Eqs (8.38) and (8.39) since both c and c −1 will be larger than p −1.
Under isobarothermal conditions it simplifies to
x
α
c−1
x
β
1
..x
ε
c−2
dµ
c−1
+
x
α
c
x
β
1
..x
ε
c−2
dµ
c
= 0. (8.45)
We may thus evaluate the slope dµ
c
/dµ
c−1
for the one-dimensional phase field in the
constant T and P section of the phase diagram. We can see that it is completely defined
by the ratio of two subdeterminants of the complete composition determinant.
Foratwo-phase equilibrium in a ternary system at constant T and P, the equation
reduces to
dµ
2
dµ
3
=−
x
α
3
x
ε
1
− x
α
1
x
ε
3
x
α
2
x
ε
1
− x
α
1
x
ε
2
=−
z
α
3
− z
ε
3
z
α
2
− z
ε
2
. (8.46)
This is an example where the final result is simplified by introducing the z variables
defined as z
i
= x
i
/x
1
. This equation was derived in a more direct way when ternary
systems were discussed in Section 8.7.Wecould apply the present method to two-phase
equilibria in general, obtaining
c
2
z
α
i
− z
β
i
dµ
i
=−
S
α
m1
− S
β
m1
dT +
V
α
m1
− V
β
m1
dP (8.47)
c
2
z
α
i
− z
β
i
d(µ
i
/T ) =
H
α
m1
− H
β
m1
d(1/T ) +
V
α
m1
− V
β
m1
dP
T. (8.48)
Exercise 8.11
Calculate the change of µ
O
for the Al + Al
2
O
3
two-phase equilibrium when the pressure
is increased. The densities of the phases are 2.7 and 3.5 g/cm
3
, respectively.
Hint
Since p = 2 and also c = 2, we have the case p = c and there is a relation between
d(µ
c
/T), d(1/T) and dP.Itisthus necessary to define the problem better. Let us assume
that the intention was to keep T constant.
Solution
Let Al be α: V
α
m
= (1/2.7) · 27 = 10 cm
3
/mole of atoms. Let Al
2
O
3
be β: V
β
m
=
(1/3.5) · (102/5) = 5.8cm
3
/mole of atoms. (∂(µ
O
/T )/∂ P)
T
= (x
α
1
V
β
m
− x
β
1
V
α
m
)/
T (x
α
1
x
β
2
− x
β
1
x
α
2
) = (1 · 5.8 − 0.4 · 10)/ T (1 · 0.6 − 0) = 3/T cm
3
/mol K.
Since T = constant, J = Nm and Pa = N/m
2
we get (∂µ
O
/∂ P)
T
= 3 ×
10
−6
J/molPa.

8.9 Extremum in temperature and pressure 181
8.9 Extremum in temperature and pressure
For convenience we shall now use the relation derived from the Gibbs–Duhem relation
in its ordinary form, i.e. we shall use S instead of H.
For p = c we obtain, by rearranging the terms in the determinants,
−
x
α
1
x
β
2
..x
δ
c−1
S
ε
m
dT +
x
α
1
x
β
2
..x
δ
c−1
V
ε
m
dP
=
x
α
1
x
β
2
..x
δ
c−1
x
ε
c
dµ
c
. (8.49)
Suppose the composition determinant on the right-hand side is zero, i.e., suppose
x
α
1
x
β
2
..x
δ
c−1
x
ε
c
= 0. (8.50)
Under isobaric conditions this would yield dT/dµ
c
= 0 for the linear phase field obtained
in the µ
c
, T phase diagram and the phase field must go through a temperature extremum.
Equation (8.50)isthus the requirement for an extremum to occur and it can also be
written in the following form because x
i
= 1ineach phase,
1 x
β
2
..x
δ
c−1
x
ε
c
= 0. (8.51)
This is a well-known equation from the theory of determinants and shows that the phases
fall on the same point (i.e. have the same composition) for c = p = 2, they fall on a
straight line for c = p = 3, on a plane surface for c = p = 4, etc. The first two cases
are described by Konovalov’s and von Alkemade’s rules, respectively (see Sections 10.8
and 10.9). Furthermore, if one knows that there is such a temperature extremum under
isobaric conditions, then one can conclude that the composition determinant must be zero
and the equation shows that there will also be a pressure extremum under isothermal
conditions. For a binary case, c = p = 2, this is illustrated in Fig. 8.23.
For p = c − 1 we obtain
−
x
α
1
x
β
2
..x
δ
c−2
S
ε
m
dT +
x
α
1
x
β
2
..x
δ
c−2
V
ε
m
dP
=
x
α
1
x
β
2
..x
δ
c−2
x
ε
c−1
dµ
c−1
+
x
α
1
x
β
2
..x
δ
c−2
x
ε
c
dµ
c
. (8.52)
In order to obtain an extremum in T at constant P (and thus in P at constant T), it is now
necessary that two determinants are zero,
x
α
1
x
β
2
..x
δ
c−2
x
ε
c−1
= 0 (8.53)
x
α
1
x
β
2
..x
δ
c−2
x
ε
c
= 0. (8.54)
Forabinary system this condition has no meaning because p = 1. For p = 2 and c =
3itimplies that the two phases fall on the same point in the composition plane (in
agreement with a generalization of Konovalov’s rule), for p = 3 and c = 4itimplies
that the three phases fall on a straight line in the composition volume (in agreement with
a generalization of Alkemade’s rule), etc. For a ternary system this can be demonstrated
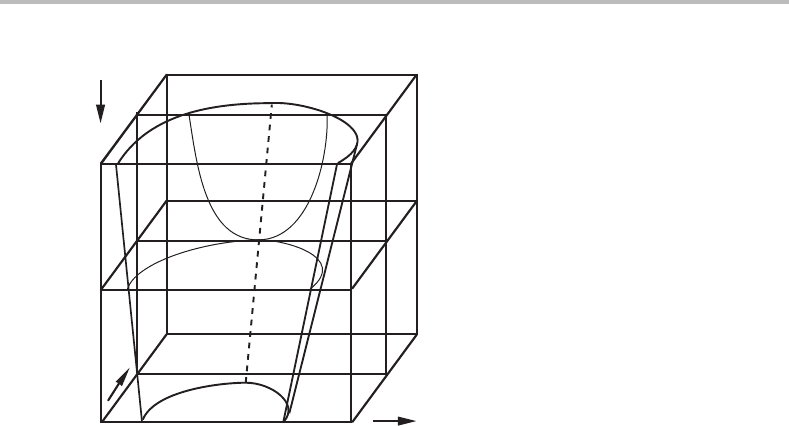
182 Phase equilibria and potential phase diagrams
P
µ
2
α
α
β
T
Figure 8.23 Potential phase diagram for a binary system showing a divariant phase field having a
T extremum in an isobaric section (see thin horizontal curve). It follows that an isothermal
section will show a P extremum (see thin vertical curve).
easily
x
α
1
x
β
2
= 0 (8.55)
x
α
1
x
β
3
= 0. (8.56)
By adding the two equations we get
0 =
x
α
1
x
β
2
+ x
β
3
=
x
α
1
1
= x
α
1
− x
β
1
. (8.57)
or x
α
1
= x
β
1
.Byinserting this in the Eqs (8.55) and (8.56) we get x
α
2
= x
β
2
and x
α
3
= x
β
3
and, consequently, also
x
α
2
x
β
3
= 0. This case is illustrated in Fig. 8.24 which may be
regarded as a diagram corresponding to the P section through the diagram in Fig. 8.23 but
with one more axis due to the third element. It follows from Eq. (8.52) that here will also
be an extremum in P under isothermal conditions but we would need four dimensions
to show a diagram corresponding to the whole diagram in Fig. 8.23.
For p = c − 2 the conditions for an extremum in T at constant P (and thus in P for
constant T)isobtained as a set of three determinants equal to zero and this means that
the compositions of the phases fall on the same point for p = 2 and c = 4, same line for
p = 3 and c = 5, same plane for p = 4 and c = 2, etc.
Exercise 8.12
Consider a three-phase equilibrium at 1 bar in a ternary system between pure A, a com-
pound B
1
C
1
and a third phase with variable composition. Can this equilibrium go through
a T maximum? Under what conditions?
8.9 Extremum in temperature and pressure 183
T
µ
C
µ
B
α
β
Figure 8.24 Potential phase diagram showing a divariant phase field with a T extremum at a
certain combination µ
B
,µ
C
. The complete phase diagram has been sectioned at a constant P.
Hint
Notice that p = 3 and c = 3 and thus c = p.
Solution
0 =
x
α
1
x
α
2
x
α
3
x
β
1
x
β
2
x
β
3
x
γ
1
x
γ
2
x
γ
3
=
1 x
α
2
x
α
3
1 x
β
2
x
β
3
1 x
γ
2
x
γ
3
=
10 0
10.50.5
1 x
γ
2
x
γ
3
= 0.5x
γ
C
− 0.5x
γ
B
,
or x
γ
B
= x
γ
C
. The variable phase must fall on the straight line between A and B
1
C
1
in
order for a T extremum to occur. However, we cannot tell if it will be a T maximum or
minimum.
Exercise 8.13
Consider a ternary system where the potential of the third component is kept constant
(by means of a high diffusivity and equilibrium with an external reservoir). The pressure
is also kept constant. Suppose one will thus find that there is a maximum temperature for
a certain α + β equilibrium. What conclusion can be drawn regarding the compositions
of the two phases? What would be the most convenient composition variable to use in
such a case?
Hint
p = c − 1. Equation (8.52)was derived for that case. Under constant P and µ
c
it yields
x
α
1
x
β
2
..x
δ
c−2
x
ε
c−1
dµ
c−1
=−
x
α
1
x
β
2
..x
δ
c−2
S
ε
m
dT .

184 Phase equilibria and potential phase diagrams
Solution
At the T maximum, the equation yields |
x
α
1
x
β
2
..x
δ
c−2
x
ε
c−1
|=0 and for a
ternary system |
x
α
1
x
β
2
|=0orx
α
1
/x
α
2
= x
β
1
/x
β
2
. The ratio of components 1 and 2 is
thus the same in the two phases. The most convenient composition variable in this case
is u
i
= x
i
/(1 − x
c
) since u
1
+ u
2
+···+u
c−1
= 1 and we find
u
α
1
u
β
2
..u
δ
c−2
u
ε
c−1
=
1 u
β
2
..u
δ
c−2
u
ε
c−1
= 0.
Foraternary system we get
1 u
β
2
= u
α
2
− u
β
2
= 0.
