Hillert M. Phase Equilibria, Phase Diagrams and Phase Transformations: Their Thermodynamic Basis

Подождите немного. Документ загружается.

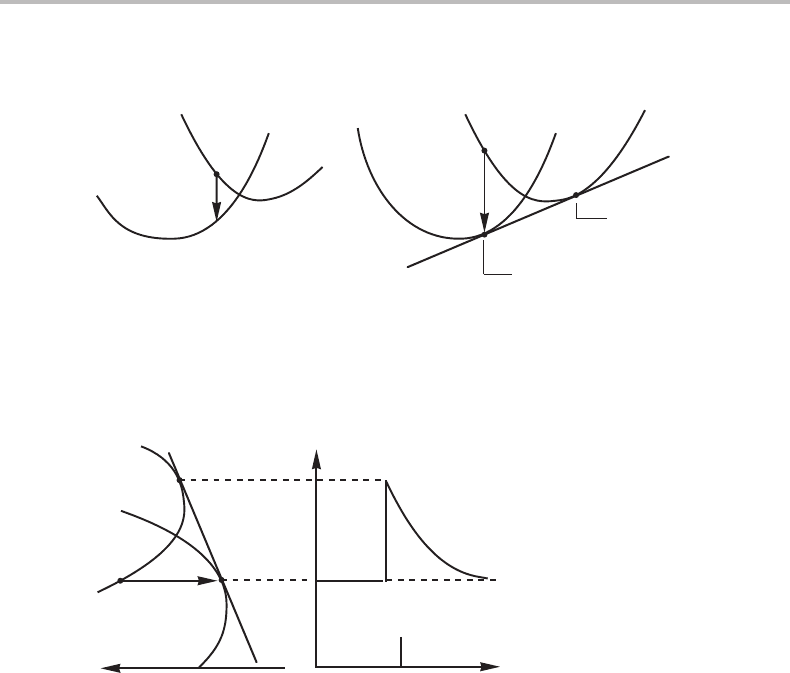
7.8 Partitionless transformation under local equilibrium 145

−∆G

(a) (b)

−∆G

α/β

= x

βο

β/α

Figure 7.20 (a) Change in Gibbs energy for a partitionless β → α transformation. (b) A

partitionless transformation under local equilibrium. Here the whole decrease in Gibbs energy

drives the diffusion in the matrix phase, β. The quantity x

βo

is the initial composition of the β

alloy and also the equilibrium composition of α.

αβ

−∆G

Figure 7.21 Use of the common-tangent construction to ﬁnd the boundary conditions for the

diffusion process.

of the growing phase. It should be realized that the local-equilibrium assumption implies

that there is a gradient within the parent phase, as illustrated in Fig. 7.21. There the

composition axis has been turned vertically in order to demonstrate how the molar

Gibbs energy diagram can yield the boundary conditions for diffusion.

Figure 7.21 demonstrates that the local-equilibrium assumption implies that there is a

pile-up of one of the components in front of the migrating interface. After an induction

period during which this pile-up is being built, one could expect a steady-state process

in which the rate of migration and the composition proﬁle stay constant. As the interface

migrates through the system and pushes the pile-up forward, it makes material of the

initial alloy composition move up on the pile-up and on the top it will be deposited

on the growing phase, the composition of which is here assumed to be equal to the

initial one. During this process the material passes through regions of higher and higher

alloy content. In each such region the chemical potentials can be described by the end-

points of the tangent to the G

curve at the local composition. The value of G

for the

material we consider will be found on that tangent and at the initial composition. It is thus

evident that the material will gradually decrease its Gibbs energy by an amount −G

corresponding to the arrow in the G

diagram. The length of the arrow represents the

146 Applications of molar Gibbs energy diagrams

α/β

= x

βο

β/α

diff

int

=∆PV

Figure 7.22 Partitionless β → α transformation under local equilibrium and under a pressure

difference, respectively.

integrated driving force dissipated by diffusion in the pile-up. Under our assumptions,

all the driving force is used to drive the diffusion and the transformation is completely

diffusion controlled.

In rapid transformations an appreciable driving force may be required in order to

make the phase interface move with the high speed. A driving force may also be required

in order to balance the pressure difference across a curved phase interface, caused by

its surface energy, 2σ/ρ. The total driving force on the interface, D

int

,may actually be

regarded as a pressure difference P = D

int

.Inavery crude but useful approach it

is assumed that the rate of migration, υ,ofaninterface is proportional to the net pressure

difference,

υ = M ·  P

net

= M · (D

int

− 2σ/ρ), (7.50)

where M is the mobility of the interface, σ is the speciﬁc surface energy and ρ is the

radius of curvature, assuming a spherical shape.

The part of the driving force acting on the interface, D

int

, has an effect on the local

equilibrium between the two phases, as illustrated in Fig. 7.22. The G

curve for the

growing phase is lifted by an amount D

int

relative to the curve for the parent phase

as if there actually were a pressure difference D

int

. Due to this construction, the

equilibrium composition of the growing phase is displaced and the local-equilibrium

assumption now requires that the parent phase is initially even more supersaturated and

falls on the other side of the equilibrium composition of the growing phase, i.e. inside

its one-phase ﬁeld. The amount of driving force dissipated by diffusion will in general

be higher than before.

Exercise 7.10

Consider the partitionless growth of α into a small spherical β particle of radius ρ in

a binary alloy. Suppose there is local equilibrium at the interface and no driving force

is required in order to make the interface move at a velocity υ. Make a reasonable

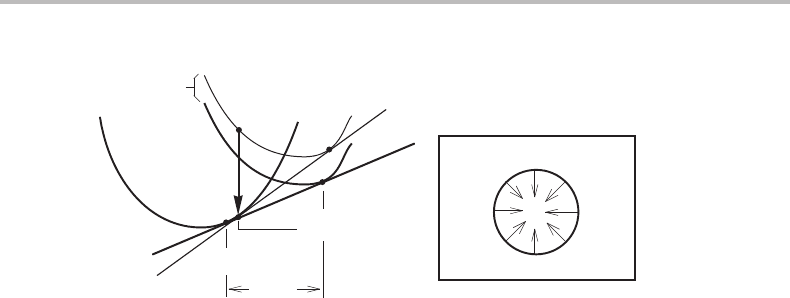
7.9 Activation energy for a ﬂuctuation 147

α+β

α/β

diff

int

= V

∆P

= x

βο

Figure 7.23 Solution to Exercise 7.10.

construction in a G

diagram illustrating that this could occur at an alloy composition

inside the α + β two-phase region.

Hint

The surface energy, σ ,may lift the G

curve for β.

Solution

The solution is presented in Fig. 7.23.

7.9 Activation energy for a ﬂuctuation

Sometimes one is interested in the formation of a ﬂuctuation for which the driving force

is negative. In such cases one instead talks about the activation energy.For the moment,

we shall make two assumptions: (i) the ﬂuctuation is only in composition, not in structure;

and (ii) the size will not be prescribed. We have already demonstrated that a system is

not stable against ﬂuctuations in composition if d

/dx

is negative. We shall now

consider the case of a positive curvature, Fig. 7.24. The activation energy per mole of

atoms in a ﬂuctuation x

is represented by G

in the diagram. By introducing the

curvature of the G

curve we directly obtain an approximate expression if both Henry’s

and Raoult’s laws hold,

G

∼



x



· d



∼



x



· RT



∼



x



· RT



. (7.51)

However, in this case we should examine the validity of the approximation by also

carrying out an exact calculation. By comparing with the evaluation of the driving force

for the precipitation of a new phase we ﬁnd without any approximation

G

= G

− x

= x



− G



+ x



− G



, (7.52)

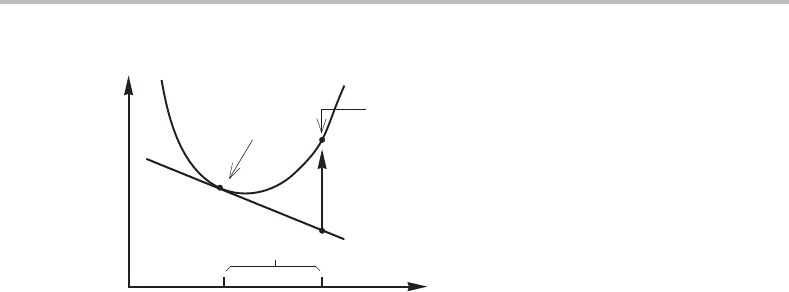
148 Applications of molar Gibbs energy diagrams

initial α

∆G

composition of

small fluctuation

∆x

Figure 7.24 Molar Gibbs energy diagram for a ﬂuctuation in composition.

where the superscript f denotes the ﬂuctuation. Henry’s and Raoult’s laws yield

G

∼









+ x







. (7.53)

For |x

− x

|x

 1weobtain approximately

G

∼



− x





. (7.54)

This is in agreement with the previous approximation, Eq. (7.51).

Exercise 7.11

Consider a binary liquid with 0.1% of B in A at 1273 K. Evaluate the activation energy

for the formation of ﬂuctuations with 0.05 and 0.15% of B, respectively. Express the

results as joule per mole of atoms in the ﬂuctuations.

Hint

It might be justiﬁed to use a dilute solution approximation but not the special approxi-

mation for |x

− x

|x

Solution

(a) G

= RT[0.9995 ln(0.9995/0.9990) +0.0005 ln(0.0005/0.0010)] = 1.625RT.

(b) G

= RT[0.9985 ln(0.9985/0.9990) + 0.0015 ln(0.0015/0.0010)] = 1.147RT.

Notice that the approximate equation would have given:

(a) G

= 0.5RT(0.0010 − 0.0005)

/0.0005 = 2.646RT.

(b) G

= 0.5RT(0.0010 − 0.0015)

/0.0015 = 0.882RT.

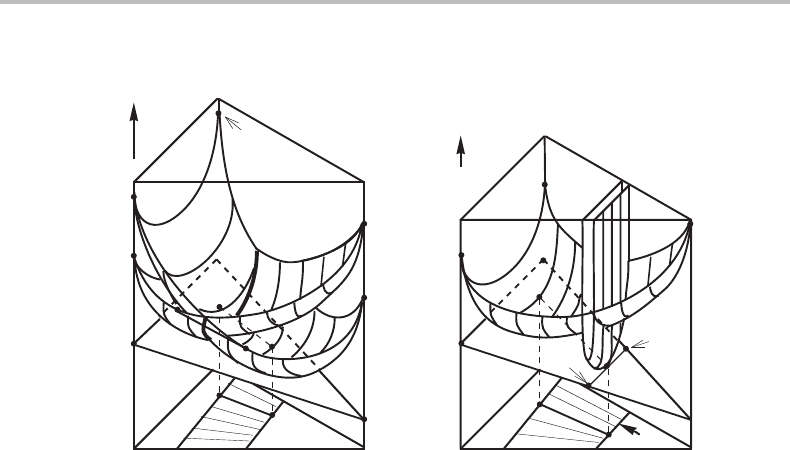
7.10 Ternary systems 149

(a) (b)

Figure 7.25 Molar Gibbs energy diagram for a two-phase equilibrium in a ternary system. The

two-phase ﬁeld is created by the common tangent-plane rolling under the two surfaces. (a) Two

ordinary solution phases. (b) One ordinary solution phase, α, and one solution between two

compounds.

7.10 Ternary systems

The property diagram for G

at constant T and P as function of the molar content

in a ternary phase is a three-dimensional diagram with a surface like a canopy. It can

be shown that for a stable phase it is everywhere convex downwards and Fig. 4.9 was

drawn in accordance with that fact. In that diagram the tangent plane to an alloy was

also drawn, the intersections of which give the partial Gibbs energies in the alloy, i.e.

the chemical potentials. We shall now apply such diagrams to various cases of phase

equilibria.

Equilibrium between two phases requires that they have the same value for the chem-

ical potential of each component. In a binary system this leads to the common-tangent

construction where the intersections with the sides represent the chemical potentials. In

a ternary system it leads to a common tangent-plane construction where the intersec-

tions with the three edges represent the chemical potentials. With the two Gibbs energy

surfaces given, one can allow this tangent plane to roll under them and thus describe a

series of possible equilibrium situations, each one represented by a tie-line between the

two tangent points in the plane. The result will be a two-phase ﬁeld, formed by projection

on the compositional triangle (see Fig. 7.25(a) where one tie-line is projected).

The general equilibrium condition in a ternary system is of course G

= µ

= G

= µ

= G

and G

= µ

= G

. These three equations leave one degree of freedom

for the two-phase equilibrium since each phase can vary its composition by two degrees

of freedom. The two-phase region in a ternary phase diagram will thus be an area covered

by tie-lines. Each tie-line connects two points, representing the coexisting phases in a

150 Applications of molar Gibbs energy diagrams

possible state of equilibrium. This conclusion still holds even if there is a restriction to

the variation in composition of one of the phases but the equilibrium equations will then

be modiﬁed, as we shall now see.

Let us ﬁrst consider the equilibrium between a solution of compounds and an ordinary

solution phase. It can be illustrated with the molar Gibbs energy diagram in Fig. 7.25(b).

It should be noticed that here a + c = 1 because the diagram is for one mole of atoms.

The construction shows that the equilibrium condition can be derived by considering

two of the sides of the triangular tangent plane

= aµ

+ cµ

= aG

+ cG

(7.55a)

= aµ

+ cµ

= aG

+ cG

. (7.55b)

These equilibrium conditions leave one degree of freedom because there are two equa-

tions and three possible variations in composition, one for the solution of compounds

and two for the ordinary solution phase. By taking the difference between the equations

we ﬁnd that



− G



a = G

− G

. (7.56)

Let us next consider the equilibrium between two solutions of compounds, θ and φ, with

the formulas (A, B)

and (A, B)

,where a + c = 1 = b + d. The previous type

of equation applies to each one of these phases although the chemical potentials on the

right-hand side cannot be referred to any one of the phases but are simply the chemical

potentials of the two-phase equilibrium.

= aµ

+ cµ

= aµ

+ cµ

= bµ

+ dµ

= bµ

+ dµ

By eliminating the unknown potentials we ﬁnd a single equilibrium condition



− G



a = µ

− µ



− G



b. (7.57)

We have thus found that there will again be one degree of freedom because now there

are two possible variations in composition, one for each line compound. If one selects a

composition for one phase, the composition of the other one is given by this equation.

The result will be similar but mathematically more complicated if the two solution phases

are formed by the mixing of a different pair of components.

Exercise 7.12

Consider the equilibrium between a solution phase (A, B)

and a stoichiometric com-

pound A

in a ternary system. Show how the chemical potential of the element C

can be calculated.

7.11 Solubility product 151

Hint

For the stoichiometric compound, φ, there is only one relation. For the solution phase,

θ, there are two. Find a combination of Gs that eliminates µ

and µ

Solution

= lµ

+ mµ

+ nµ

; G

= aµ

+ cµ

; G

= aµ

+ cµ

. Elimi-

nate µ

and µ

by taking a

−lG

− mG

,which is found to be equal to

(an − cl − cm)µ

.Weobtain µ

= (a

−lG

− mG

)/(an − cl − cm).

7.11 Solubility product

According to Eq. (3.18) the Gibbs energy of a phase φ is always related to the chemical

potentials µ

by the following relation



, (7.58)

where x

represents the composition of the phase. When the phase is a compound, the

composition is constant and it is described by the indices in the formula, e.g. l,m,n in

.For one mole of formula units we have, if l + m + n = 1,

= lµ

+ mµ

+ nµ

. (7.59)

The superscript

is used in order to indicate that the value refers to the compound itself,

the ‘pure compound’, and not to a compound phase, diluted by other components being

dissolved in it.

Figure 7.26 illustrates the equilibrium between a compound φ and a solution phase, α.

There is only one equilibrium condition and it is obtained by inserting the partial Gibbs

energies of the solution phase instead of the chemical potentials in the last equation. So,

= lG

+ mG

+ nG

(7.60)

Let us consider the solubility curve of φ in α close to the A corner and introduce

activities instead of chemical potentials. The activity a

is deﬁned through the equation

+ RT ln a

, (7.61)

where

is the molar Gibbs energy of some reference state for i. Eq. (7.59) yields



−l

− m

− n



RT = l · ln a

+ m · ln a

+ n · ln a

. (7.62)

Using the standard Gibbs energy of formation of the φ phase from the pure components

in their reference states, which is equal to the expression in parentheses, we get

exp









= (a

)

. (7.63)

152 Applications of molar Gibbs energy diagrams

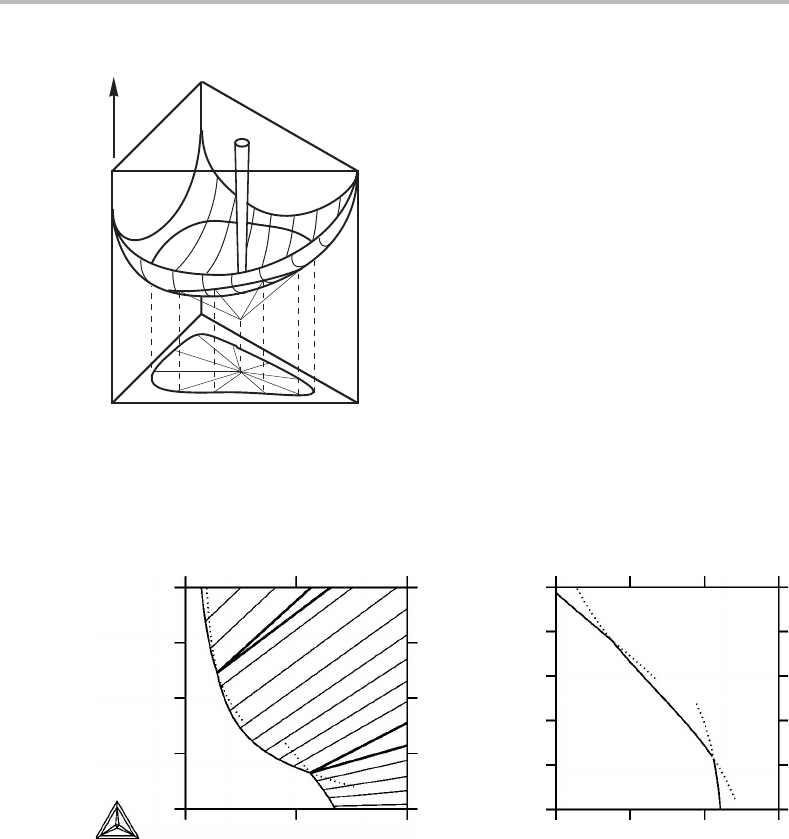
Figure 7.26 Molar Gibbs energy diagram for a ternary system with an ordinary solution phase, α,

and a ternary stoichiometric phase, φ.

0.20

(a) (b)

0 0.10

γ+M

−1.5

−4.0

−5 −2

In(x

)

In(x

)

γ+M

Figure 7.27 Isothermal and isobaric section of the Fe–Cr–C phase diagram near the Fe corner.

The solubility curves for strictly stoichiometric compounds would have been straight lines in the

logarithmic diagram (b) and hyperbolic in the linear diagram (a).

In a dilute solution the activity of minor components is approximately proportional to the

content expressed, for instance, as the molar content. The activity of the major component

is approximately unity and can thus be omitted from the equations. Thus,

exp









= (a

)

. (7.64)

The left-hand side is often denoted by K and is regarded as the solubility product. The

solubility curve for a compound in a terminal solution may thus be approximated by a

7.11 Solubility product 153

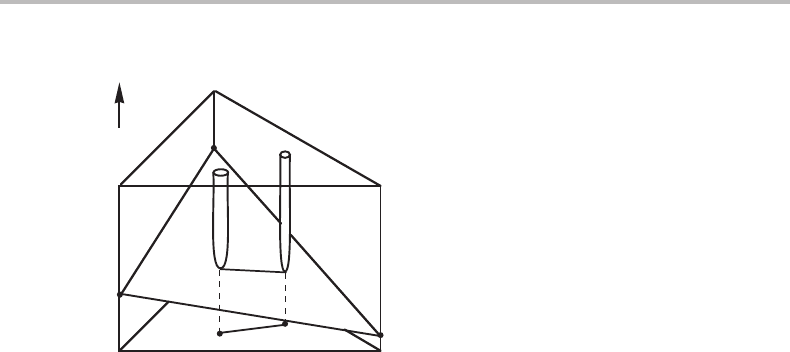
Figure 7.28 Solution to Exercise 7.13.

hyperbolic curve in a linear phase diagram and with a straight line in a logarithmic phase

diagram. As an example, in Fig. 7.27 an isobarothermal section of the phase diagram

Fe–Cr–C is presented. The diagram shows the solubilities of three carbides in γ.Inthe

logarithmic diagram the solubility lines are almost straight although the compositions

of the carbides are not quite constant.

Exercise 7.13

Consider the equilibrium between two ternary stoichiometric phases. Even though the

compositions are ﬁxed, there is a degree of freedom from a thermodynamic point of view

because there must be three chemical potentials. After a value has been chosen for one

of them, the other two are ﬁxed. Derive equations for their calculation.

Hint

There are only two equations relating the three potentials, one for each phase. Choose

one of the potentials as the independent one and eliminate one of the other two.

Solution

Write the two conditions as

= aµ

+ bµ

+ cµ

and

= lµ

+ mµ

+ nµ

A Gibbs energy diagram demonstrates that there is indeed one degree of freedom

(Fig. 7.28). We can thus take any value of µ

, for instance, and then express the other

two in µ

. After eliminating µ

by multiplying the ﬁrst equation with m and the other

with b and subtracting, we get µ

= [m

− b

+ (bn − cm)µ

]/(am − bl) and

in the same way µ

= [l

− a

+ (an − cl)µ

]/(bl − am).

154 Applications of molar Gibbs energy diagrams

−1

−2

−3

−2

−1

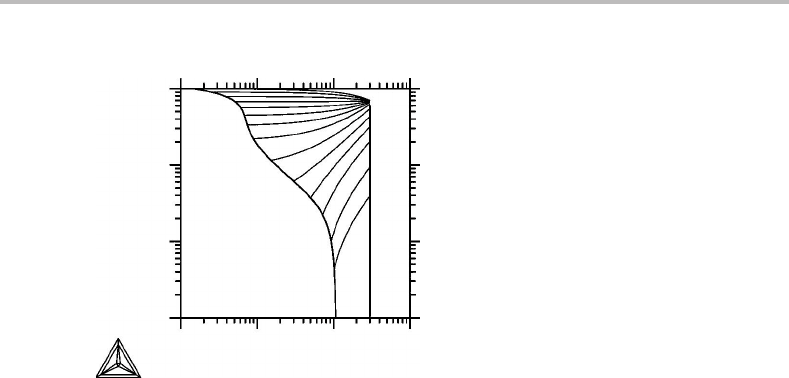
Figure 7.29 Solution to Exercise 7.14.

Exercise 7.14

Sketch the whole γ + M

two-phase ﬁeld in Fig. 7.27 and include a series of tie-lines.

Hint

Tie-lines are straight lines in diagrams with linear scales. When the scales are changed

to logarithmic, only those tie-lines remain straight that are horizontal or vertical or have

a slope of unity.

Solution

The solution is given in Fig. 7.29.