Hillert M. Phase Equilibria, Phase Diagrams and Phase Transformations: Their Thermodynamic Basis

Подождите немного. Документ загружается.

7.4 Two-phase equilibria in binary systems 135

α is stable

α+β is stable

β is stable

(b)(a)

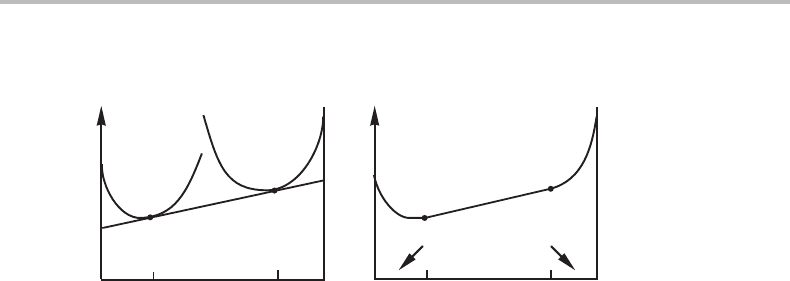
Figure 7.10 The common-tangent construction for ﬁnding the compositions of two phases in

equilibrium at given T and P.

Solution

Let the amounts of the components be N

, N

and N

in the old description and



, N



and N



in the new one. Denote the chemical potentials in the new description

with µ



. The mass balance for each element gives N

= N



, N

= 3N



and N



+ N



We thus get







= µ

+ µ

= µ

3dN



+ µ



+ µ



+ µ



= (3µ

+ µ

)dN



+ µ



Thus, µ



= µ

, µ



= µ

and µ



= 3µ

+ µ

7.4 Two-phase equilibria in binary systems

In a two-phase equilibrium we have the following two conditions at constant T and P

because the chemical potential for each component must be the same in the two phases.

= µ

= G

(7.27)

= µ

= G

. (7.28)

It is evidentthat these conditions can be satisﬁed onlybya common tangent,asillustrated

in Fig. 7.10(a). The lowest possible G

for each composition is shown in Fig. 7.10(b) and

it is evident that some mixture of α + β represents the stable state for an alloy between

the two tangent points.

Forastoichiometric phase with its well-deﬁned composition, it is not possible to

deﬁne the chemical potentials since one can draw different tangents without changing

the composition of the point of tangency markedly. On the other hand, the chemical

potentials of a phase can be deﬁned by equilibrium with a second phase. Figure 7.11(a)

illustrates this case when the second phase is a solution phase or (b) another stoichiometric

phase. When it is a solution phase, we obtain

= x

· G





+ x

· G





. (7.29)

136 Applications of molar Gibbs energy diagrams

(a) (b)

Figure 7.11 Molar Gibbs energy diagram showing the equilibrium between (a) a stoichiometric

phase and a solution phase and (b) between two stoichiometric phases.

By solving this equation, one can determine the composition of the solution phase, β,

and from the known properties of β one can then calculate µ

and µ

.InFig. 7.11(b)

both phases, θ and φ, are stoichiometric phases, and we obtain the following relations

= x

+ x

; µ

− x

(7.30)

= x

+ x

; µ

− x

. (7.31)

These equations also apply to the equilibrium between two solution phases if the G

and G

are evaluated for the equilibrium compositions.

Exercise 7.5

In a binary system, where the mutual solubilities are very small, there are two stable

stoichiometric phases α(A

) and β(AB

). Calculate the chemical potential of B in a

50 : 50 alloy in terms of the quantities G

and G

. Base the calculation on a construction

in the G

diagram.

Hint

Remember that the Gibbs energy of a two-phase state falls on the common tangent.

Start by drawing a solid line representing all stable states. It should show that both

stoichiometric phases are stable.

Solution

Evidently, the alloy is α + β (see Fig. 7.12). With x

= 0.6 and x

= 0.25 the con-

struction gives µ

= µ

α+β

= G

+ (G

− G

) · (x

− 0)/(x

− x

) = G

+ (G

−

) · 60/(60 − 25) = (60/35)G

− (25/35)G

7.5 Allotropic phase boundaries 137

α+β

Figure 7.12 Solution to Exercise 7.5.

T =T

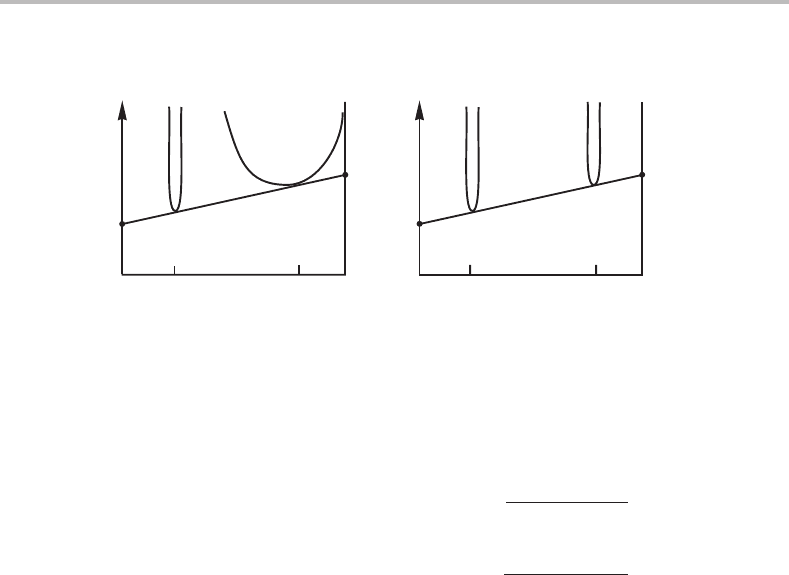
Figure 7.13 The relation between Gibbs energy curves of two phases and their two-phase ﬁelds in

the phase diagram. The dashed line is the so-called T

line or allotropic phase boundary.

7.5 Allotropic phase boundaries

One can sometimes draw a line inside a two-phase region to show where the two phases

would have the same Gibbs energy value if they had the same composition. It is the critical

limit for a hypothetical diffusionless phase transformation. Such a transformation is very

similar to an allotropic transformation in a pure element and the line, sometimes called

the allotropic phase boundary,isoften denoted by T

. This name is derived from the

word ‘allotropy’, i.e. the property of a substance of being found in two or more forms.

Figure 7.13 illustrates the relation between the allotropic phase boundary and the molar

Gibbs energy diagram.

Exercise 7.6

Consider a binary system with three phases of variable compositions and in a eutectic

equilibrium (see Section 12.5) with each other. Show reasonable positions of the three

allotropic phase boundaries. Extrapolate all of them below the eutectic temperature.

138 Applications of molar Gibbs energy diagrams

α+β

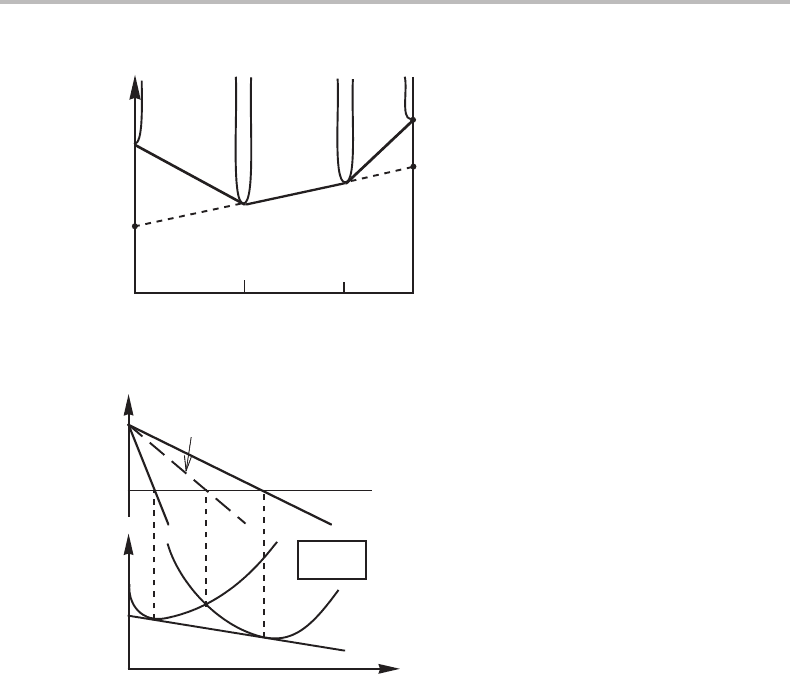
Figure 7.14 Solution to Exercise 7.6.

Hint

Consider in particular howthe three allotropic phase boundaries intersect each other when

extrapolated. Will there be one or three points of intersection? It may be instructive to

sketch a molar Gibbs energy diagram.

Solution

It is evident that T

α+L

and T

L+β

will intersect inside the α + β phase ﬁeld. Consider

a G

diagram (Fig. 7.14)atthe eutectic temperature, showing one G

curve for each

phase (thick lines in the lower portion of the ﬁgure). Each one of the three intersections

is a point on a T

line. When the temperature is decreased, the L curve is lifted (see thin

line) relative to the other two until all three curves ﬁnally intersect in one point. There

the three T

lines will intersect. In the phase diagram (upper portion) we should thus

draw the T

α+β

line through the intersection of the other two.

7.6 Effect of a pressure difference on a two-phase equilibrium

In order to illustrate the effect of pressure, we shall consider an incompressible phase,

β. The application of a hydrostatic pressure will lift up its Gibbs energy curve by the

amount P

. This is illustrated in Fig. 7.15(a). Since V

is usually dependent on the

composition, the curve will be somewhat deformed. The construction with a tangent will

yield P

and P

where V

and V

are deﬁned from V

in the same way as G

and G

are deﬁned from G

(see Fig. 4.6).

The relative position of the Gibbs energy curves for different phases can change with

pressure due to differences in the molar volumes. The equilibrium conditions can thus

be modiﬁed by the application of a hydrostatic pressure. This effect is even stronger if

the pressure is applied to one of the phases only, which may happen due to the effect

7.6 Effect of a pressure difference on a two-phase equilibrium 139

(a) (b)

∆x

)

(0)

Figure 7.15 (a) Effect of a hydrostatic pressure on the molar Gibbs energy of a single phase. The

phase is assumed to be incompressible. (b) The effect of pressure in a stoichiometric phase on

the equilibrium composition of a coexisting phase not under pressure.

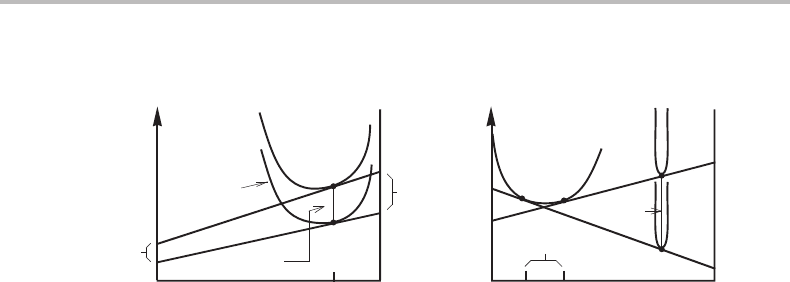
of surface energy in a curved interface. In Fig. 7.15(b) the phase under pressure is

a stoichiometric phase and its molar Gibbs energy is increased by P

.Wemay,for

instance, imagine that the phases are contained in a cylinder where the balance of surface

energies, σ ,atthe wall of the cylinder gives a constant radius of curvature ρ = 2σ/P

The diagram illustrates that the solubility of θ in α is increased due to the pressure

in θ, assuming ordinary pressure in α.Itshould be emphasized that this case must be

treated with care because the two phases are under different pressures and the law of

additivity does not apply to the Gibbs energy unless special precautions are taken. This

was mentioned in Section 3.4 and will be discussed in Section 16.7.However, in applying

the common-tangent construction we have only made use of the deﬁnition of the chemical

potentials.

The effect on the solubility can be estimated if one knows the curvature of the G

curve. The difference in slope between the two tangents can be estimated as [x

α/θ

) −

α/θ

(0)] · d

/dx

if the change in composition is small. If the distance between the

two phases is reasonably constant, we obtain, by multiplying with that distance,



− x



α/θ

) − x

α/θ

(0)



· d



(7.32)

α/θ

) − x

α/θ

(0) = P



− x



. (7.33)

When α is a dilute solution we may approximate d

/dx

with RT/x

α/θ

according to

Eq. (7.19) and obtain

α/θ

) − x

α/θ

(0) = P

α/θ





− x



. (7.34)

This equation is often applied to a spherical interface and 2σ/r is then substituted for P

In that form it is known as the Gibbs–Thomson equation. For large changes in solubility

one should integrate over the pressure increase and allow x

α/θ

on the right-hand side to

vary during the integration. For an inﬁnitesimal increase in P

we get

α/θ



α/θ







− x



· dP

. (7.35)

For the case where (x

− x

)isreasonably constant integration yields



α/θ

)



α/θ

(0)



= P





− x



. (7.36)

140 Applications of molar Gibbs energy diagrams

(a)

(b)

(0) G

(0)

) G

)

∆x

∆G

∆x

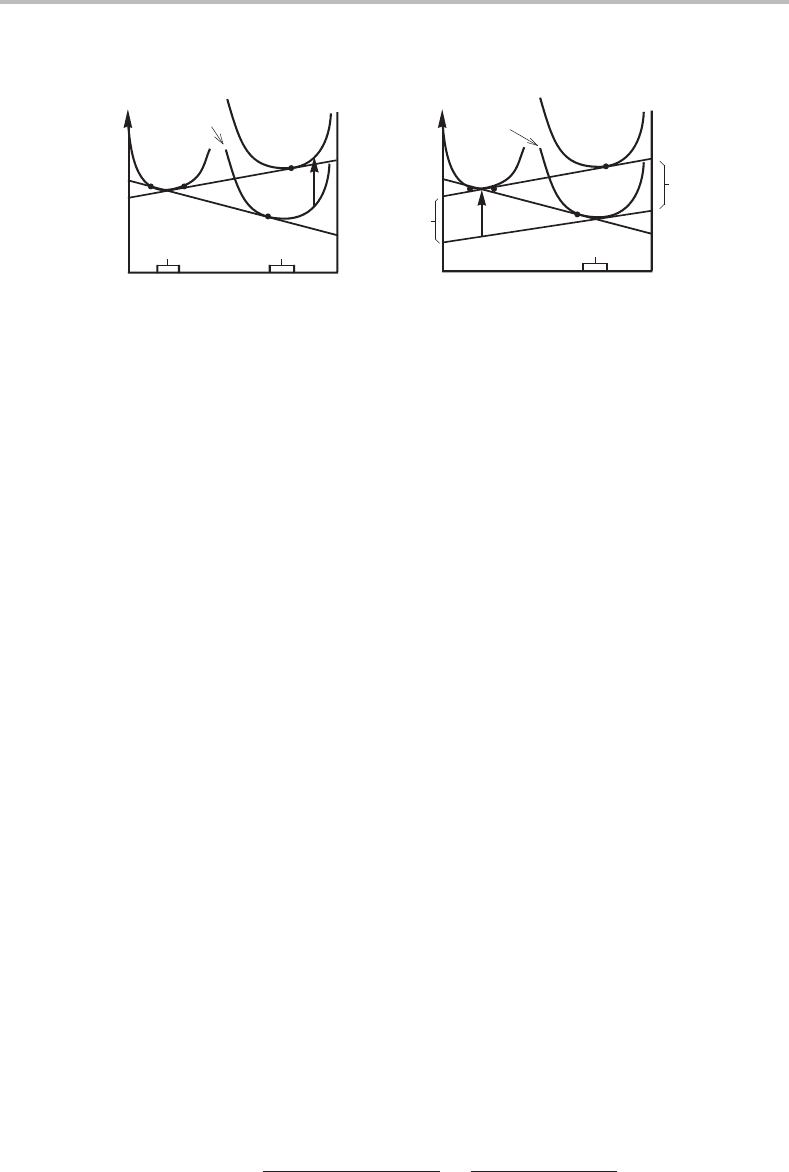
Figure 7.16 Molar Gibbs energy diagram illustrating the change in composition of a phase, β,

under pressure when in equilibrium with another phase, α.

If the phase under pressure can also vary in composition, its equilibrium composition

will also change. This case is illustrated in Fig. 7.16. The change in composition of the

phase under pressure can be evaluated from Fig. 7.16(b) where a tangent to the initial

curve has been drawn for the β composition of the new equilibrium. The diagram

deﬁnes a quantity G

which is given as

G

= P



+ x



, (7.37)

but also as

G



− x



· d





β/α

) − x

β/α

(0)



, (7.38)

if d

/dx

is reasonably constant. By equating the two expressions we obtain

β/α

) − x

β/α

(0) = P



+ x



− x



· d





. (7.39)

If the β phase is a dilute solution of B in A, then x

+ x

is approximately equal

to the molar volume for pure A in the β state, which we shall simply denote by V

, and

/dx

can be approximated by RT/x

according to Eq. (7.19), yielding

β/α







− x



· dP

. (7.40)

We can take into account the effect of P

on both phases if they are both dilute solutions

of B in A but then we cannot treat x

− x

as a constant. However, the expressions for

α/β

and dx

β/α

are identical for two dilute solutions,

α/β



α/β

= dx

β/α



β/α

. (7.41)

Integration yields

α/β

)



α/β

(0) = x

β/α

)



β/α

(0) (7.42)

β/α

) − x

α/β

)

β/α

)

β/α

(0) − x

α/β

(0)

β/α

(0)

. (7.43)

7.6 Effect of a pressure difference on a two-phase equilibrium 141

The quantity on the left-hand side appears in the equation for dx

β/α

with a slightly

different notation, (x

− x

)/x

. This ratio can thus be treated as a constant during the

integration of dx

β/α

, yielding

β/α

) − x

β/α

(0) =







· x

β/α



− x



(7.44)

α/β

) − x

α/β

(0) =







· x

α/β



− x



. (7.45)

It should again be emphasized that the equations in the present section were derived only

for an incompressible phase.

Exercise 7.7

The precipitation of Sn from a supersaturated solid solution of Sn in Pb sometimes

results in a lamellar aggregate of a Sn phase with very little Pb and a Pb phase with

less Sn. The aggregate, comprising alternate layers, grows into a Pb-rich matrix of the

original composition. Experimental studies have been made of the coarseness of such

a structure in terms of a quantity w, the combined width of one lamella of each phase.

When discussing theoretical predictions the measured w is compared with the critical

value w

∗

which would completely stop the growth of the Sn phase because, due to

the effect of surface energy, it would put this phase under such a high pressure that

it would be in equilibrium with the original Pb matrix in spite of its supersaturation.

This pressure can be calculated from the effect of surface energy. In one study an alloy

with x

= 0.112 was investigated at a temperature where the equilibrium value was

0.06. The investigators assumed that the new phase had the equilibrium composition,

= 0.06, and using the Gibbs–Thomson equation for large changes they calculated

∗

from w

∗

= 2σ V

/RT ln(0.112/0.06). They found that the observed w was about

100 times larger than w

∗

instead of twice according to a simple theory. Check their

calculation.

Hint

Make a careful analysis of what pressure the surface energy will impose on the Sn

phase under the simplifying assumption that the Pb lamellae are not under an increased

pressure.

Solution

The pressure in the Sn phase will balance the surface energy, which gives a force of 2σL

if L is the length of the lamella. The area of the edge is fw

∗

L if f is the fraction of the Sn

phase. Thus, P

∗

L = 2σ L. The lever rule gives f = (0.112 − 0.06)/(1 − 0.06) =

0.055. Now relate the pressure to the change in solubility, ln(0.112/0.06) = P

∗

/RT

(1 – 0.112)

∼

∗

/RT. Combining these equations yields w

∗

= 2σ /P

∗

f = 2σ V

/fRT

ln(0.112/0.06). The investigators missed the factor f ( = 0.055) which explains most of

the discrepancy.

142 Applications of molar Gibbs energy diagrams

(a) (b)

alloy

D =−∆G

−∆G

Σx

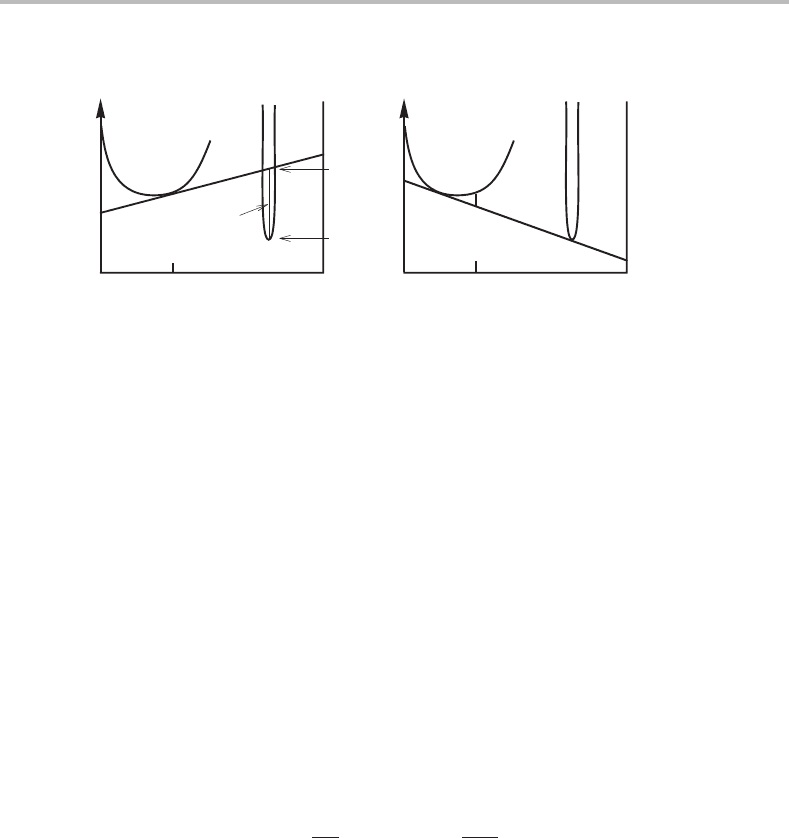
Figure 7.17 (a) Molar Gibbs energy diagram. (b) Method for evaluation of the driving force for

the formation of a new phase θ from a supersaturated β solution.

7.7 Driving force for the formation of a new phase

When we take some A and B away from a large quantity of a solution phase, α,itislike

taking them from one reservoir each, with the chemical potentials equal to G

and G

respectively. As long as the amount of the α phase is large, we can take A and B in any

proportion without changing the values of G

and G

.Wecan thus form a small amount

of a new phase, θ,ofany composition without changing the Gibbs energy of the whole

system, provided that the new phase falls on the α tangent. If the new phase falls below

the tangent, the decrease counted per mole of atoms in the new phase is obtained as

− G

= x

· G





+ x

· G





− G





. (7.46)

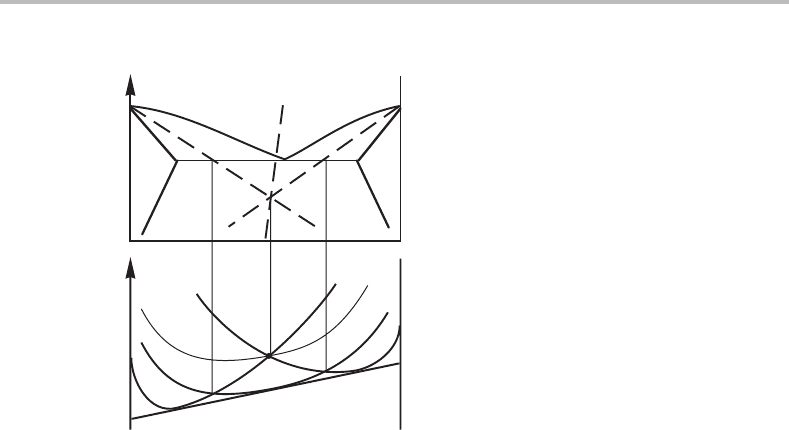
This is illustrated in the molar Gibbs energy diagram in Fig. 7.17(a).Byconvention,

the change of Gibbs energy accompanying a reaction is deﬁned as G

= G

products

−

reactants

.Itisevident that the decrease in Gibbs energy, −G

,isequal to the driving

force for the precipitation of the θ phase from a supersaturated β solution, counted per

mole of θ,ifthe extent of the reaction, ξ,isexpressed as the number of moles of θ, N

D =−



∂G

∂ξ



T,P,N

=−



∂G

∂ N



T,P,N

=−G

. (7.47)

The magnitude of the driving force for the precipitation of θ from a supersaturated

α solution, counted per mole of θ, can be estimated from the supersaturation x

almost the same way as the effect of pressure on solubility was evaluated. By comparing

Fig. 7.17(a) with Fig. 7.15(b) we obtain from Eq. (7.32)

D =−G

= P

= x

· d





− x



. (7.48)

This is the driving force at the start of the precipitation of θ.Asthe process continues,

the supersaturation will decrease gradually and so will the driving force. It may thus be

interesting to evaluate the integrated driving force which should represent an average

value for the whole process. The method of evaluation is illustrated in Fig. 7.17(b).

One usually evaluates the integrated driving force for the transformation of the whole

system, i.e. the difference in Gibbs energy between the ﬁnal α + θ mixture and the initial

supersaturated α.Itissimply given by the short vertical line in Fig. 7.17(b).

7.7 Driving force for the formation of a new phase 143

(a) (b)

−∆G

= x

−G

) + x

−G

) −∆G

max

= G

−G

−∆G

Figure 7.18 Solution to Exercise 7.8.

Exercise 7.8

Consider the formation of a small amount of β from a large reservoir of α under condi-

tions such that the reservoir has the potentials G

and G

and the new phase has G

and

(accepting that such conditions can somehow be realized). (a) Construct a reasonable

molar Gibbs energy diagram and use it for deriving an expression for the driving force

per mole of β phase. Express the result in terms of the potentials and the compositions

of the two phases. (b) Suppose the composition of α has been decided. How should one

choose the composition of β in order to get the largest driving force?

Hint

(a) Using the given potentials one can draw the tangents to the two Gibbs energy curves.

Evaluate the distance between them at the proper composition. (b) In this exercise, the

tangent to the α curve is given. The question is how we can ﬁnd the point on the β

curve which lies as low as possible relative to the α tangent. In principle, it can be found

without drawing the corresponding β tangent but it would be most helpful to do so, so

long as one draws that tangent correctly.

Solution

(a) See Fig. 7.18(a). (b) One should choose the composition obtained from a parallel

tangent construction (see Fig. 7.18(b)).

Exercise 7.9

Show with the construction in Fig. 7.17(b) the magnitude of the integrated driving force

counted per mole of the θ phase formed.

Hint

The magnitude is −G

/ f

if f

is the ﬁnal fraction of θ in the alloy. The question is

how to ﬁnd this by construction. Notice that f

can be found graphically using the lever

rule.

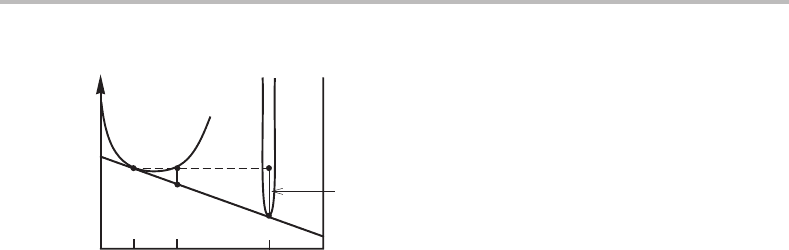
144 Applications of molar Gibbs energy diagrams

−∆G

)(f

)

−∆G

Figure 7.19 Solution to Exercise 7.9.

Solution

Draw a straight line joining the ﬁnal α and the initial α (Fig. 7.19). Extend the line to the

composition of θ. Also use the tangent to the ﬁnal α point shown in Fig. 7.17(b). Read

the distance between intersections on the θ composition.

7.8 Partitionless transformation under local equilibrium

So far, we have mainly considered stationary states and for a state with more than

one phase we have assumed equilibrium between the phases, which is a reasonable

approximation after a long enough time at a high enough temperature. The situation is

quite different during a phase transformation but it is still common to assume that full

equilibrium is established locally at the phase interface even when it is migrating through

the material. This was introduced in Section 3.10 and is called the local-equilibrium

approximation and will now be our starting point for an examination of partitionless

transformations. The local conditions at migrating interfaces will be further discussed

in Chapter 14.

When a β →α transformation occurs in an alloy without any difference in composi-

tion between the reactant phase (also called parent phase) and the product phase (also

called daughter phase or growing phase), it is regarded as a partitionless transformation.

The two phases will fall on the same vertical line in the molar Gibbs energy diagram.

Figure 7.20(a) shows the construction for a binary system. Under constant T and P, the

driving force is given by the vertical distance between two points representing the initial

β and the growing α

D = G

− G

=−G

. (7.49)

It is evident that the partitionless transformation cannot possibly occur under local equi-

librium unless the composition of the phases falls on the left-hand side of the point of

intersection between the two G

curves.

Whether or not a transformation can actually occur under the conditions illustrated in

Fig. 7.20(a) will be discussed in Section 14.4.Anattractive possibility is illustrated in

Fig. 7.20(b).Itisbased on the assumption of local equilibrium at the interface and that

is why the common-tangent construction is used here. This illustration presumes that the

parent phase is so supersaturated that its composition falls on the equilibrium composition