Hillert M. Phase Equilibria, Phase Diagrams and Phase Transformations: Their Thermodynamic Basis

Подождите немного. Документ загружается.

6.9 Le Chatelier’s principle 125

Exercise 6.9

Test Le Chatelier’s principle on the change of temperature and pressure when an amount

of heat is added to a two-phase system of water vapour and liquid water under constant

volume. Suppose that evaporation is initially very slow due to a thin ﬁlm of oil.

Hint

Remember that dU = dQ–PdV.Atconstant V we thus have dU = dQ and could choose

U as the variable that is changed by an action from the outside. Its conjugate variable

is–1/T. The internal variable ξ may be identiﬁed with the amount of vapour.

Solution

Identify U with X

and − 1/T with Y

.For a stable system we get, at constant ξ,

i.e. before any change of the amount of vapour, 0 < (∂(−1/T )/∂U)

. This means that

−1/T, and thus also T, has increased due to the increase of U.

At the higher temperature the equilibrium vapour pressure will be higher. In a second

stage of the process there will thus be evaporation and the temperature will decrease in

agreement with Le Chatelier’s principle, 0 < (∂(−1/ T )/∂U )

D=0

< (∂(−1/T )/∂U)

On the other hand, the pressure has increased during the ﬁrst stage due to the heating

of the vapour present from the beginning. During the second stage, the pressure will

increase further, in apparent contradiction to Le Chatelier’s principle. However, pressure

is not conjugate to U,which was the variable that was changed to a new value in the

experiment.

The result is far from trivial because there would be further evaporation during the

second stage only if the increase in pressure of the initial vapour due to its heating is

smaller than the increase of the equilibrium vapour pressure due to the heating of the

water. By relying upon Le Chatelier’s principle we may thus conclude that the heating of

the vapour gives a smaller increase of the pressure than the heating of the water would

increase the equilibrium vapour pressure.

Applications of molar Gibbs

energy diagrams

7.1 Molar Gibbs energy diagrams for binary systems

In this chapter we shall derive some useful thermodynamic relations relating to phase

equilibria under constant temperature and pressure, sometimes in exact form but some-

times using approximations in order to bring the ﬁnal expressions into a suitable form.

We shall see how property diagrams for the molar Gibbs energy can be used in such

derivations. Most of the applications will make use of the tie-line rule (see Section 4.5).

As an introduction, some basic properties of solutions must be discussed and, in the

present section, a simple solution model will be described. A more thorough discussion

will be given in Chapter 20.

Let us ﬁrst consider a case where a solution phase α can vary in composition over a

whole binary system from pure A to pure B. It is then convenient to compare the G

value at any composition with the value one can read on the straight line between the two

end-points, sometimes called the end-members of the solution. The difference is often

called the Gibbs energy of mixing and is denoted with a superscript M. It is illustrated

in Fig. 7.1.Itisdeﬁned by the following equation

= x

+ x

. (7.1)

Awarning should be issued regarding the interpretation of

. Usually it is deﬁned

with reference to the straight line between points representing the pure components in

the same state as the phase under consideration, i.e. the end-members of the solution.

However, sometimes it is deﬁned with reference to a different state for one of the compo-

nents, for instance the state which is most stable at the temperature under consideration.

This is illustrated in Fig. 7.1(b) where pure B is more stable as β than as α.

The Gibbs energy diagram gives information on the partial molar Gibbs energies

for the two components, i.e. the chemical potentials. For a single phase one can use

the construction explained for V

in Fig. 4.6 and illustrated for G

in Fig. 4.7.Itis

now demonstrated again in Fig.7.2(a) and is in agreement with the following relations,

which are examples of the more general expression for all partial quantities, derived in

Section 4.1.

= G

+ (1 − x

)dG

/dx

= G

+ x

/dx

(7.2)

− G

= dG

/dx

. (7.3)

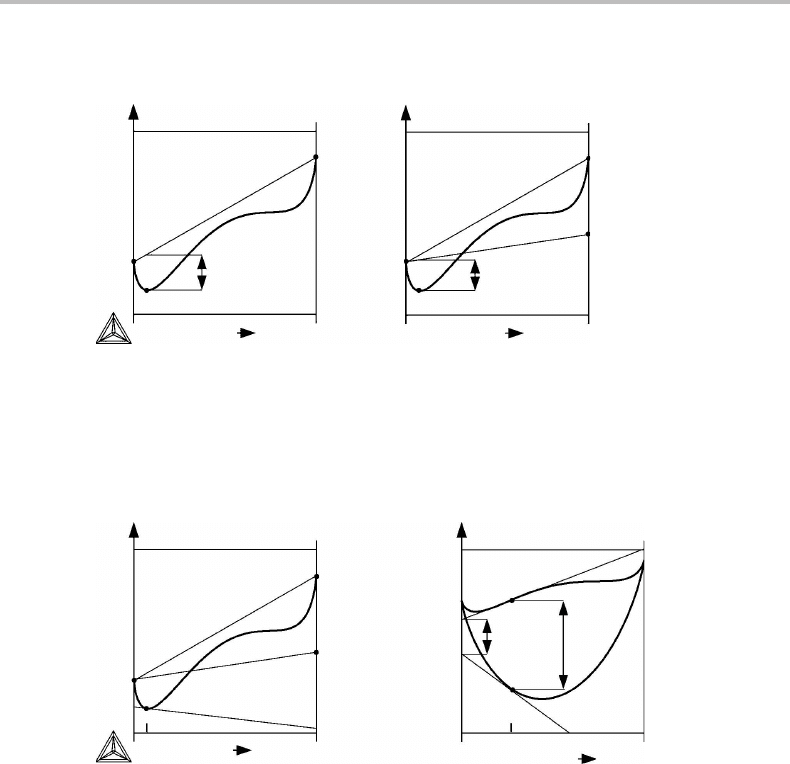
7.1 Molar Gibbs energy diagrams for binary systems 127

(a) (b)

−G

−G′

Figure 7.1 Molar Gibbs energy diagram for a binary system illustrating the deﬁnition of the

Gibbs energy of mixing. The end-members of the solution are used as references in (a) but a

more stable state of B is used in (b).

(a) (b)

(x ′

)

x ′

0 1.0

(x ′

)

ideal

(x ′

)

(x ′

)

x ′

Figure 7.2 (a) Tangent construction to obtain a chemical potential. (b) Deﬁnitions of excess

quantities for an alloy of composition x



An important contribution to the Gibbs energy of mixing comes from the entropy of

mixing of the two kinds of atoms. In Section 19.8 we shall consider the case where they

are distributed at random and shall ﬁnd that the entropy of mixing of one mole of atoms

will then be −R(x

ln x

+ x

ln x

). A solution with only this contribution to the Gibbs

energy of mixing is regarded as an ideal solution

idealα

= x

+ x

+ RT(x

ln x

+ x

ln x

). (7.4)

Using Eq. (4.5) relating partial quantities to molar quantities we obtain

idealα

+ RT ln x

. (7.5)

A comparison with the ideal solution is given in Fig. 7.2(b). The curve for G

ideal

shows

that the term RT(x

ln x

+ x

ln x

)isnegativeand makes the G

curve look like a

hanging rope. It is the main cause of the stability of solutions.

128 Applications of molar Gibbs energy diagrams

It is common to summarize all other contributions to the Gibbs energy with a term

called the excess Gibbs energy and denoted by

= G

ideal

= x

+ x

+ RT(x

ln x

+ x

ln x

) +

. (7.6)

This is also illustrated in Fig. 7.2(b).Inthe same way we may deﬁne the mixing and

excess quantities for the partial Gibbs energies,

= G

ideal

+ RT ln x

. (7.7)

= RT ln x

. (7.8)

It is evident that the mixing and excess quantities can be calculated directly in the same

way as G

+ (1 − x



− x



(7.9)

+ (1 − x



− x



. (7.10)

It should be emphasized that one cannot give an absolute numerical value to the partial

Gibbs energies,

, because there is no natural zero point for Gibbs energy.

Numerical values can be given only to differences in Gibbs energy between two states.

Thus we can give a value to G

−

, and another value to G

−

,where pure

α–B and pure β–B are regarded as two different choices of reference states for B. Such

avalue gives the vertical distance between two points (see the B-axis in Fig. 7.2(a)).

For alloys, a numerical value can be given only to differences between two states of the

same composition. The two lines representing

and



in Fig. 7.1(a) and (b),

respectively, are thus vertical. This stems from the fact that one cannot compare the

Gibbs energies for A and B. When starting to construct such a diagram one can give the

−

line any convenient slope.

If one has chosen the end-members of an A–B solution to deﬁne the reference states,

and

, then it is evident that the excess Gibbs energy is zero at the two sides of

the system where G

is equal to

.For a dilute solution of B in A we may

thus try to approximate

as Lx

,anexpression that goes to zero on both sides.

This is the regular solution approximation, and using the equation relating G

to G

ﬁnd

+ RT ln x

+ L

. (7.11)

It is common to introduce the chemical activity, a

, through the expression

+ RT ln a

+ RT ln x

+ RT ln f

, (7.12)

where

= f

, (7.13)

and f

is called the activity coefﬁcient of B. The activity is thus deﬁned as

= exp



−





. (7.14)

7.1 Molar Gibbs energy diagrams for binary systems 129

∆

Figure 7.3 Molar Gibbs energy diagram illustrating the deﬁnition of the standard Gibbs energy

of formation, 

,ofacompound θ.

The activity coefﬁcient is obtained through

RT ln f

. (7.15)

Foradilute solution, i.e. low x

,wemay thus write

RT ln f

= L

∼

or f

∼

exp(L

/RT). (7.16)

With this approximation, the activity is proportional to the content. This is called Henry’s

law. We also ﬁnd for low x

RT ln f

+ (1 − x



= L

∼

0. (7.17)

The value of f

is thus unity close to the A side. This is called Raoult’s law. When

Henry’s law holds for B and Raoult’s law holds for A, then we obtain



= G

− G

+ RT ln x

+ L

−

− RT ln x

(7.18)



= RT/x

+ RT/x

= RT(x

+ x

)/x

= RT/x

∼

RT/x

(7.19)

Foranintermediary phase, which does not extend to the pure components, one must

always refer the Gibbs energy to the values of the components in selected states, usu-

ally their stable states. For a phase with a well-deﬁned composition one often talks

about the standard Gibbs energy of formation (see Fig. 7.3). From that diagram we

obtain



− x

. (7.20)

This quantity is often denoted by 

or 

.Itisimportant to mention the reference

states to which it refers and also the amount of material being considered, for instance

1 mole of atoms or 1 mole of formula units (like, e.g., Cr

130 Applications of molar Gibbs energy diagrams

−RT ln0.9

−RT ln1.04

Figure 7.4 Solution to Exercise 7.1.

Exercise 7.1

An α solution in the A–B system has a

= 0.9at1000 K when pure α–B is used as

reference state. Calculate a

referred to another state of B, called β–B, which is more

stable than α–B by 1200 J/mol. Illustrate with a G

diagram.

Hint

The position of the point on the B-axis representing G

does not depend upon the choice

of reference state. We can thus equate any two expressions for G

Solution

refα

= 0.9;

+ RT ln(a

refα

) = G

+ RT ln(a

refβ

);

refβ

= a

refα

exp[(

−

)/RT] = 0.9 × exp(1200/8.3145 × 1000) = 1.04. Since

this is > 1, the α solution is supersaturated with B in comparison with the stable β state

of B (see Fig. 7.4).

Exercise 7.2

Cismetastable at all temperatures and could thus decompose into an Fe-rich phase

and graphite. At 1169 K the stable Fe phase (γ ) dissolves about 1.24 mass% C. Mea-

surements have shown that the Gibbs energy of formation of Fe

Cat1169 K is negative

(–1620 J/mole of formula units). Explain how this can be reconciled with the fact that

Cisnot stable by sketching a G

, x

diagram.

Solution

Cfalls 1620 J/mol below the line of reference between pure Fe and pure graphite

(dashed line in Fig. 7.5)but it falls above the common tangent representing the γ +

graphite equilibrium. Thus, Fe

Cismore stable than a mixture of the pure elements but

less stable than a mixture of an Fe–C solution and pure C.

7.2 Instability of binary solutions 131

graphite

Figure 7.5 Solution to Exercise 7.2.

(a) (b)

)

Figure 7.6 (a) Construction showing that a negative curvature results in a decrease of G

when

is increased. (b) Demonstration that a system between the points of inﬂexion is unstable. A

small difference in composition will increase spontaneously.

7.2 Instability of binary solutions

In Figs 7.1 and 7.2 we have sketched molar Gibbs energy curves, each with two minima

and a central region where ∂

/∂x

is negative. This region falls between two points

of inﬂexion and according to Section 6.6 they should deﬁne the limit of stability. In

Fig.7.6(a) tangents havebeen drawnat some compositions betweenthe points of inﬂexion

and it can be seen that G

decreases when x

increases. According to Eq. (6.27) this is

also a violation of the condition of stability.

The change in the total Gibbs energy of the system, when one half of the system grows

richer in A and the other one in B, is illustrated in Fig. 7.6(b). The tie-line rule requires

that the total Gibbs energy of a mixture is represented by a point on the line connecting

the points representing the two parts. Since the overall composition is not changed, the

total Gibbs energy moves down along a vertical line at the alloy composition (not shown

here). Such a system is thus unstable against ﬂuctuations in composition.

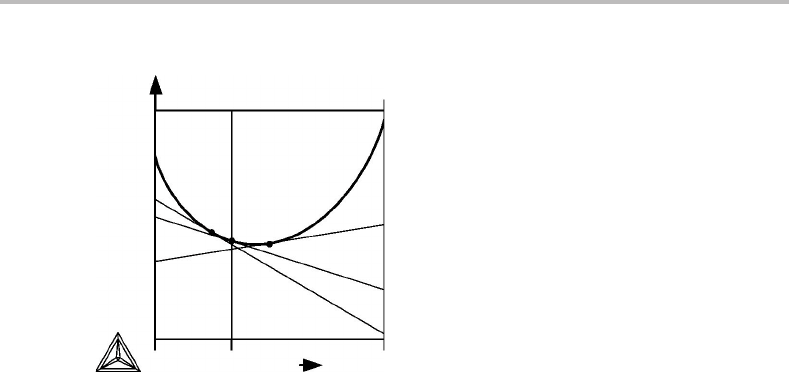
132 Applications of molar Gibbs energy diagrams

0 1.01/3

Figure 7.7 Solution to Exercise 7.3.

Exercise 7.3

In a binary solution one usually discusses two activities, a

and a

, and for a stable

system each of them increases monotonously with the content of the same component.

However, one may deﬁne the activity of an intermediary species, e.g. A

B. Prove that

also increases as the content of A

B increases in a stable system and thus has a

maximum at the very composition of A

Hint

Instead of the chemical activity, a

, let us consider the chemical potential µ

,which

is equal to 2µ

+ µ

, i.e. 2G

+ G

,or, even better, µ

2/3

1/3

, i.e. (2G

+ G

)/3). It

may be studied in a G

, x

diagram.

Solution

Forany alloy the tangent in the G

, x

diagram gives G

and G

on the two sides

and the intersection of the tangent with a vertical line at x

= 1/3 thus gives (2G

)/3. By inspection it is evident that the intersection has its highest position for the

alloy x

= 1/3 (see Fig. 7.7). Otherwise, the G

curve must have a negative curvature

somewhere.

7.3 Illustration of the Gibbs–Duhem relation

The molar Gibbs energy diagram in Fig. 7.8(a) shows a stoichiometric compound, θ,

with a well-deﬁned composition A

, possibly because it is a crystalline phase with

two sublattices. Often, the composition of such a phase cannot vary appreciably without

avery steep increase of the Gibbs energy. It is thus practically impossible to vary N

and keep N

constant and the deﬁnition of partial Gibbs energy, given in Section 4.1,

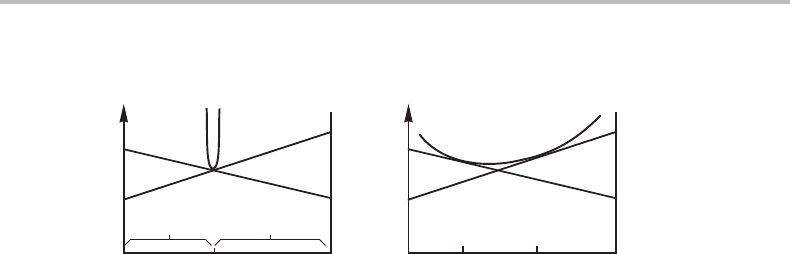
7.3 Illustration of the Gibbs–Duhem relation 133

µ′′

µ′

µ′′

µ′

′′

x ′′

x ′

(a) (b)

b = x

a = x

Figure 7.8 Molar Gibbs energy diagram for (a) a binary stoichiometric phase θ and (b) a binary

solution phase α.Ifµ

is controlled by some method, then the value of µ

is given in both cases.

cannot be used. However, the tangent construction in Fig. 7.2 can still be used. For this

case we shall prefer to talk about chemical potentials and use the notations µ

and

. The situation is not drastically different for a phase with variable composition (see

Fig. 7.8(b)). For both types of phase one may select the value of µ

and the value of µ

will then be ﬁxed. One could also talk about the chemical potential of the compound,

.From Section 4.8 we get

= µ



= aµ

+ bµ

; µ

= (µ

− aµ

)/b. (7.21)

By comparing the values deﬁned by two different tangents we ﬁnd for a stoichiometric

compound, because µ

is ﬁxed,

(µ



− µ



) + x

(µ



− µ



) = 0, (7.22)

where a = x

and b = x

if a + b is chosen as 1. This may be regarded as the Gibbs–

Duhem relation integrated for a phase with constant composition.

Foraphase with variable composition one may also select the value for µ

, and the

value for µ

will then be ﬁxed by the expression for the molar Gibbs energy,

= x

+ x

; µ

= (G

− x

)/x

, (7.23)

but here G

varies with the composition and the composition varies with the choice of

,asdemonstrated for a solution phase α in Fig. 7.8(b). The Gibbs–Duhem relation

holds

dµ

+ x

dµ

= 0, (7.24)

but not in the integrated form given for the stoichiometric compound, because the tangents

do not intersect in a point on the G

curve.

In a ternary system one may have a solution between two binary stoichiometric phases

if they are isomorphic (have the same structure). Figure7.9 shows a Gibbs energy diagram

for such a case. The composition can now be varied with one degree of freedom and we

may consider two components or end-members A

and B

This kind of solution may be represented by the formula (A, B)

and the composition

may be represented by molar contents deﬁned as

= N

/(N

+ N

), (7.25)

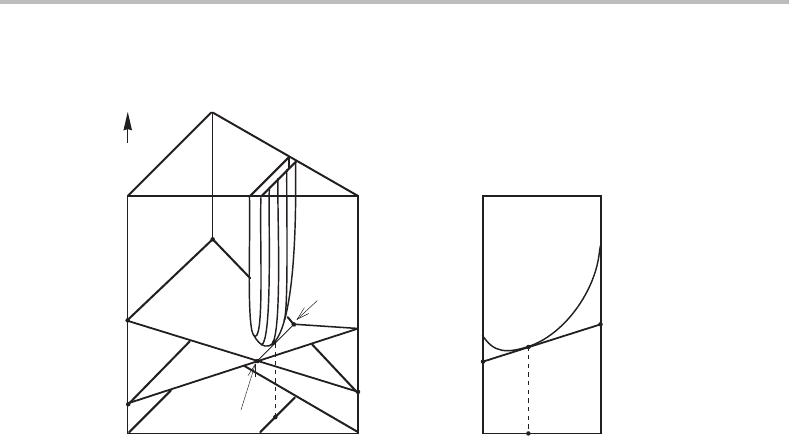
134 Applications of molar Gibbs energy diagrams

µ′

µ′′

µ′

(a) (b)

Figure 7.9 Molar Gibbs energy diagram for a ternary solution between two binary

stoichiometric phases.

where the two Ns represent the moles of formula units. Another method of representation

is based on the molar contents evaluated for each sublattice, the so-called site fractions

which were discussed in Section 4.7.

From Fig. 7.9 it is evident that the molar Gibbs energy for this kind of solution phase

can be expressed in the following ways if a + c = 1.

= x

+ x

= y

+ y

. (7.26)

The diagram in Fig. 7.9(a) with two possible tangent planes shows that the values of

and µ

are well deﬁned by the composition but µ

,µ

and µ

are not.

Exercise 7.4

Consider the chemical potential of Fe

Cinasolution phase of Fe, C and Mn, using basic

principles. Show that it is actually equal to 3µ

+ µ

by making a calculation using

Section 4.6.

Hint

In the Fe–C–Mn system we usually use Fe, C and Mn as the components but now we

should change to a new set of components. Fe

Cisone component and the others could

be C and Mn. Notice that dG =



cannot change its value just because we change

the set of components to be considered.