Hillert M. Phase Equilibria, Phase Diagrams and Phase Transformations: Their Thermodynamic Basis

Подождите немного. Документ загружается.

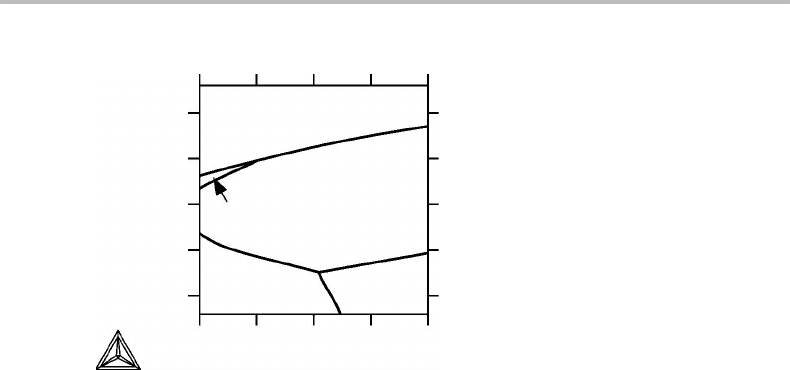
8.3 Topology of potential phase diagrams 165

2500

liq

bcc(δ) fcc(γ)

bcc(α) hcp(ε)

2000

1500

1000

500

050100

P (kbar)

T (K)

150 200

Figure 8.8 T, P phase diagram of Fe according to an assessment of experimental information.

Exercise 8.3

Derive an equation for the α + β line in a unary T, P phase diagram under the conditions

that H

and V

can be regarded as constant.

Hint

Start with Clapeyron’s relation, Eq. (8.17).

Solution

dP = (H

/V

)(dT /T ) and P − P

= (H

/V

) ln(T/T

) under constant H

and V

.Inaddition, a point on the line, T

, P

, must be known. It should be noticed

that it is sometimes more convenient to approximate S

as constant than H

. The

result is then a straight line in a linear T, P phase diagram. When one of the phases is

agas, one may approximate V

by RT/P and integration yields, if H

is constant,

lnP = K exp(−H

/T ).

Exercise 8.4

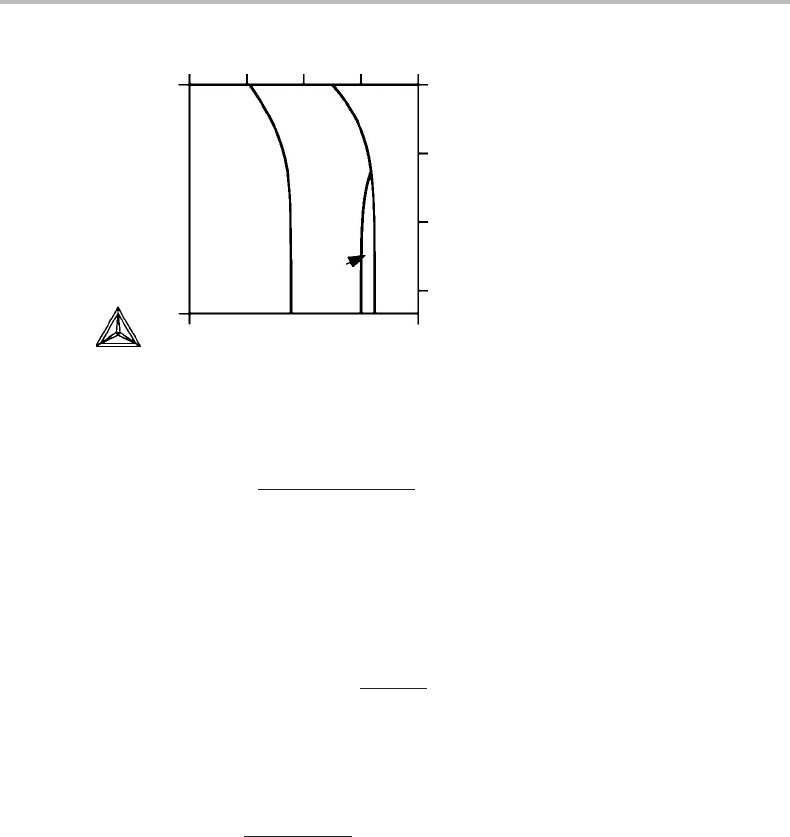
A T, P phase diagram for a unary system (pure A) is given in Fig. 8.9.Itshows four

phases. Construct a reasonable T, µ

property diagram at P

.Itshould show all the

stable and metastable two-phase equilibria at P

Hint

The T values for all the two-phase equilibria at P

are easily found by extrapola-

tion. Approximate all the T, µ

lines by straight lines, intersecting at the two-phase

equilibria.

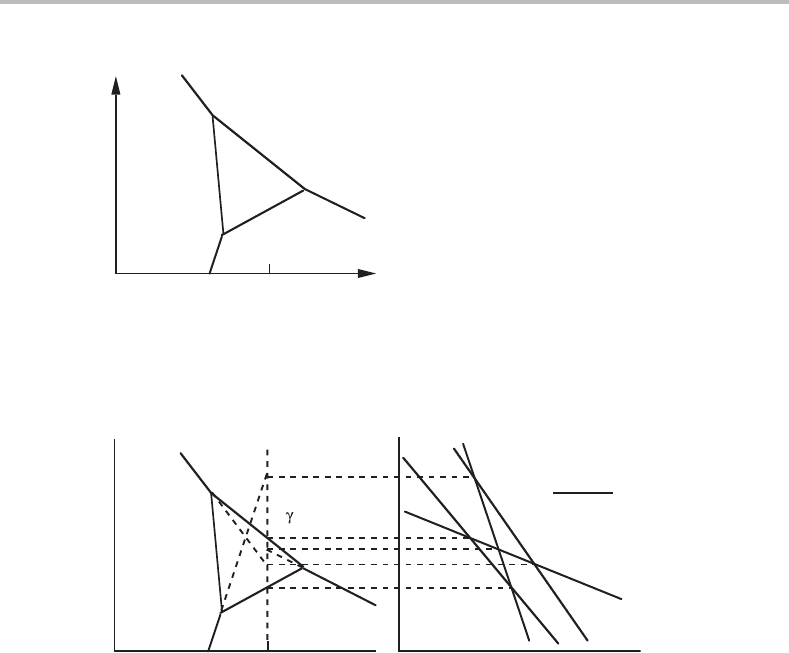
166 Phase equilibria and potential phase diagrams

Figure 8.9 See Exercise 8.4.

(a) (b)

P = P

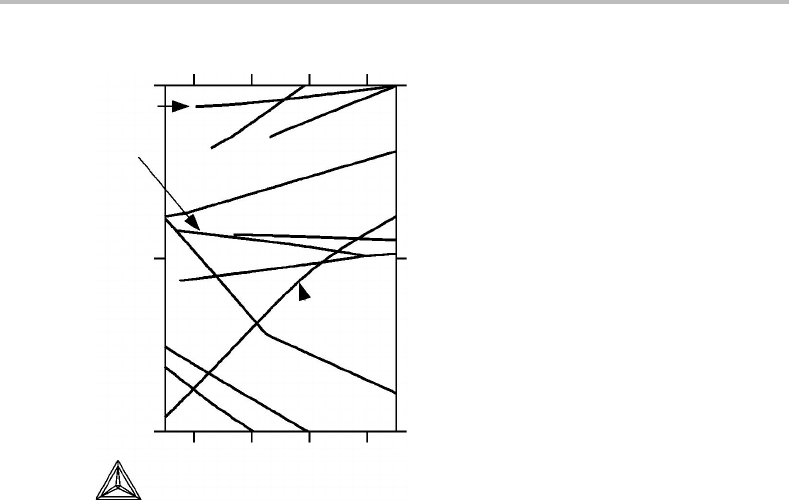
Figure 8.10 Solution to Exercise 8.4.

Solution

The solution is given in Fig. 8.10. The convex polygon close to the origin represents the

stable equilibria.

8.4 Potential phase diagrams in binary and multinary systems

So far we have discussed a system with one component, a unary system. In a binary

system we have two components and four potentials, T, −P, µ

and µ

. The fundamental

property diagram will be four-dimensional and cannot be visualized. The phase diagram

will be three-dimensional and it will be composed of four geometrical elements as

illustrated in Fig. 8.11. They are all phase ﬁelds.

(a) Points where four phases are in equilibrium. We cannot change any variable without

changing the kind of equilibrium.

(b) Lines where three phases are in equilibrium. We can change only one variable inde-

pendently without leaving the line.

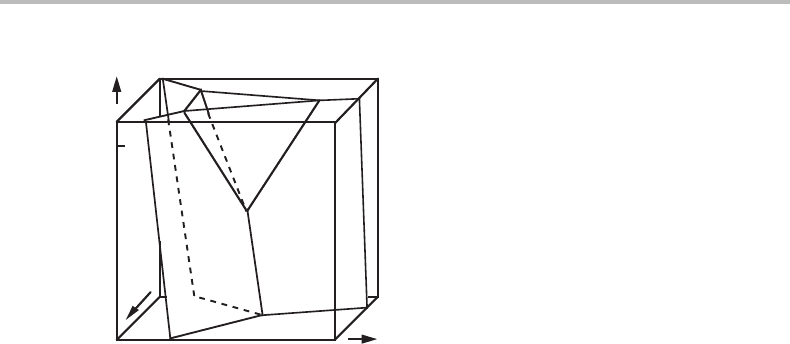
8.4 Potential phase diagrams in binary and multinary systems 167

Figure 8.11 T , P,µ

phase diagram for a binary system with four phases.

variables without leaving this phase ﬁeld.

(d) Volumes where a single phase exists. We can change three independent variables

without leaving this kind of phase ﬁeld. Its equilibrium is trivariant.

For higher-order systems, ternary, quaternary, quinary, etc., the principles will be the

same. The phase diagram will have c + 1axes, where c is the number of components.

The geometrical elements will be points, lines, surfaces, volumes, hypervolumes, etc.,

and they will represent phase equilibria which have a variance of zero, one, two, three,

four, etc., in accordance with Gibbs’ phase rule.

Suppose one wants to calculate a state of equilibrium under the requirement that it

must consist of p speciﬁed phases. Then one must, in addition, specify the values of υ

independent variables, where υ is given by Gibbs’ phase rule, υ = c + 2 − p.Onthe

other hand, suppose one wants to calculate a state of equilibrium without specifying any

phase. Then one must specify the values of υ independent variables, where υ is equal

to c + 1 because the phase diagram will have c + 1axes. That corresponds to the case

of one speciﬁed phase. This does not violate Gibbs’ phase rule because one will always

fall inside a one-phase ﬁeld, p = 1. In practice one will never be able to hit exactly on

the other types of geometrical elements.

Figure 8.3 illustrated the integrated driving force for a transition from β to α. The

same situation cannot be illustrated for a higher-order system but the integrated driving

force can be derived in the same way under conditions where T, P and all the chemical

potentials except for µ

are kept constant. The combined law yields

dµ

=−SdT + V dP −



dµ

− Ddξ =−Ddξ (8.19)



Ddξ =−N



− µ



= N



− µ



. (8.20)

It is thus necessary that µ

is lowest in the stable phase if all the other potentials are kept

constant.

168 Phase equilibria and potential phase diagrams

In the above integration it was assumed that N

is kept constant which was the way

to deﬁne the size of the system. However, it must be noted that the content of all the

other components will most probably change during a transition carried out under the

conditions considered here. It may be of more practical interest to derive the integrated

driving force for a transition under constant T, P and composition. It can be obtained

from the combined law expressed in terms of Gibbs energy,

dG =−SdT + V dP + µ

− Ddξ =−Ddξ (8.21)



Ddξ = G

− G

. (8.22)

Exercise 8.5

Trytoformulate the equivalence of the 180

◦

rule for a point where four phases coexist

in a binary three-dimensional phase diagram.

Solution

All such points must be on pointed tips. The four adjoining three-phase lines must fall

on ridges.

8.5 Sections of potential phase diagrams

In order to visualize a higher-order potential phase diagram one may decrease the

number of dimensions by making a section at a constant value of some potential, an

equipotential section. It will show exactly the same geometrical elements as a poten-

tial phase diagram for a system with one component less. One may section several

times and thus decrease the dimensions of a higher-order phase diagram until it can

be plotted as a two-dimensional diagram. It is common ﬁrst to keep P constant and

then T. One may then continue and keep the chemical potential of some component

constant.

At each sectioning one will lose the geometrical element of the lowest dimensionality.

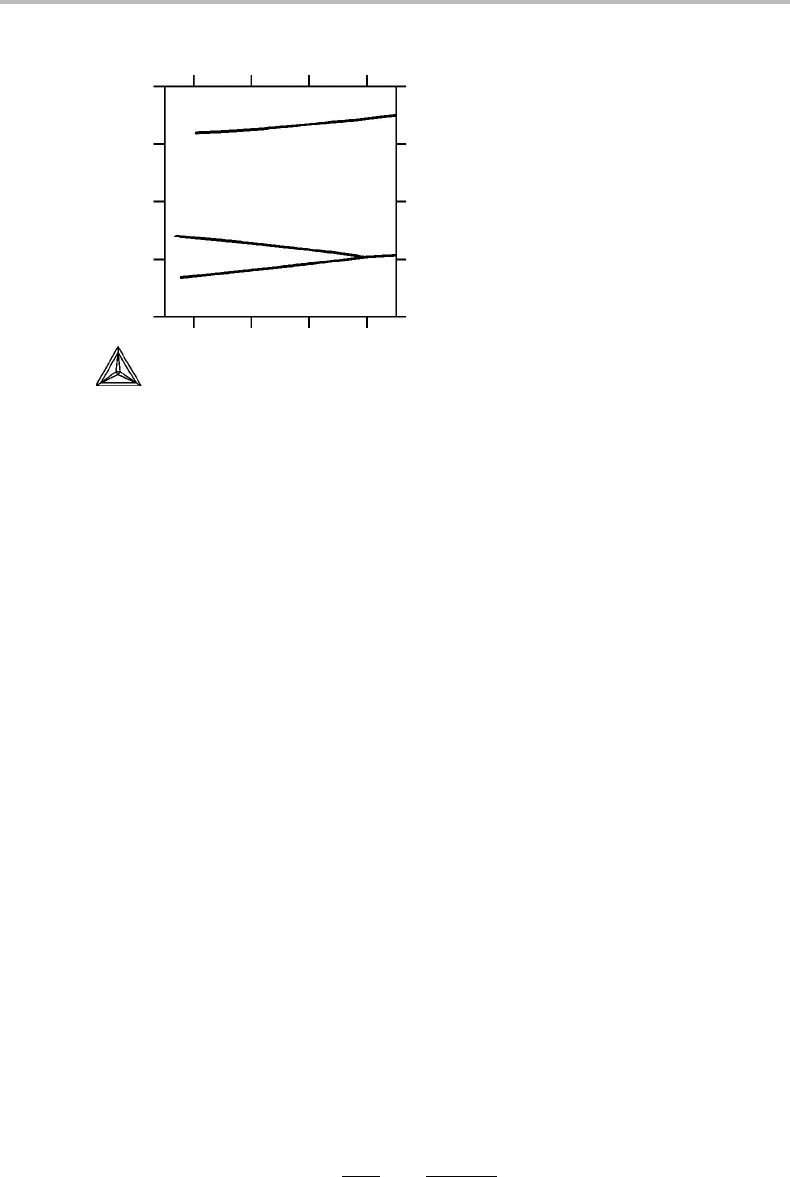
This is demonstrated in Fig. 8.12 which was obtained by taking a horizontal (T = T

)

section through the potential phase diagram in Fig. 8.11. The chance of hitting the

four-phase point is negligible and no four-phase point should be included in this type

of diagram. The topology of a diagram will thus be the same whether the number of

dimensions is decreased by sectioning at a constant value of a potential or by reducing

the number of components by one. In order to distinguish the two cases, one may call

the diagram with axes for all the independent potentials a complete potential phase

diagram.Ithasc + 1axes.

In Section 8.3 we called the geometrical elements phase ﬁelds. In the complete poten-

tial phase diagram a phase ﬁeld has the dimensions given by Gibbs’ phase rule. However,

8.5 Sections of potential phase diagrams 169

α+β+δ

α+γ+δ

β+γ+δ

α+γ

α+δ

β+δ

α+β

γ+δ

γ+β

Figure 8.12 Equipotential (isothermal) section of the potential phase diagram in Fig. 8.11 at

T = T

its dimensionality decreases by one unit for each sectioning and we obtain

d = υ − n

= c + 2 − p − n

, (8.23)

where n

is the number of sectionings. In order to avoid confusion with the variance of

a phase equilibrium, which is given by Gibbs’ phase rule and is independent of what

kind of diagram is used, this will be called the phase ﬁeld rule. The number of axes in

the diagram, r,which initially is c + 1, will also decrease by sectioning, r = c + 1 − n

and we can thus write the phase ﬁeld rule as

d = r + 1 − p. (8.24)

Phase ﬁelds for which d < 0 will normally not show up in the ﬁnal diagram, as

demonstrated by the negligible chance of hitting the four-phase point in the above

case.

It is evident from the second form of the phase ﬁeld rule that a diagram with r axes

has the same topology independent of how many sectionings of potential axes have been

used to obtain it. By inspecting a diagram without knowing the number of components,

it is thus impossible to tell if it is a section or not.

Exercise 8.6

Consider the equilibrium Fe + S(gas) ↔ FeS under a constant P. Can it exist in a range

of T ?

Solution

We have two components, Fe and S, i.e. c = 2, and three phases, Fe, gas and FeS, i.e.

p = 3. If we section at some pressure, we have n

= 1. Thus d = c + 2 − p − n

= 2 +

2 − 3 − 1 = 0. Under these conditions the equilibrium can exist only at a particular T.

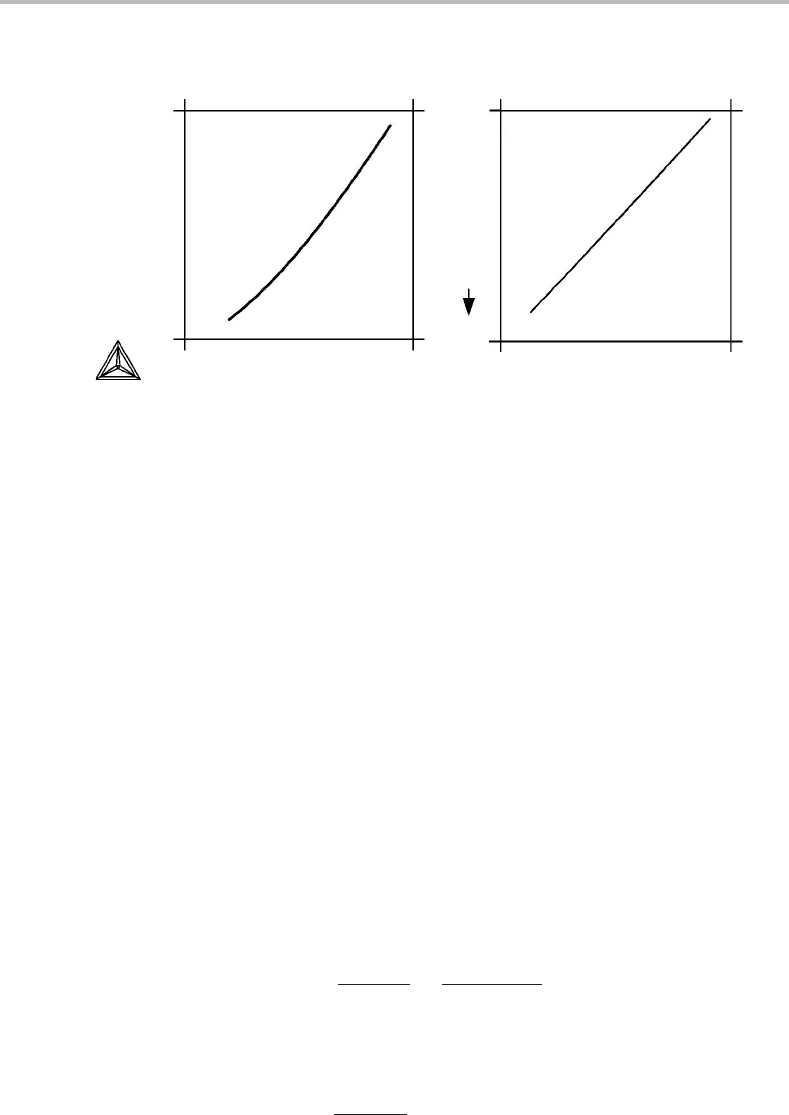
170 Phase equilibria and potential phase diagrams

1600

(a) (b)

400

bcc–W

10000/T (K

−1

)

T (K)

(µ

−

)/RTµ

−

(J/mol)

−38 −34 −10 −2

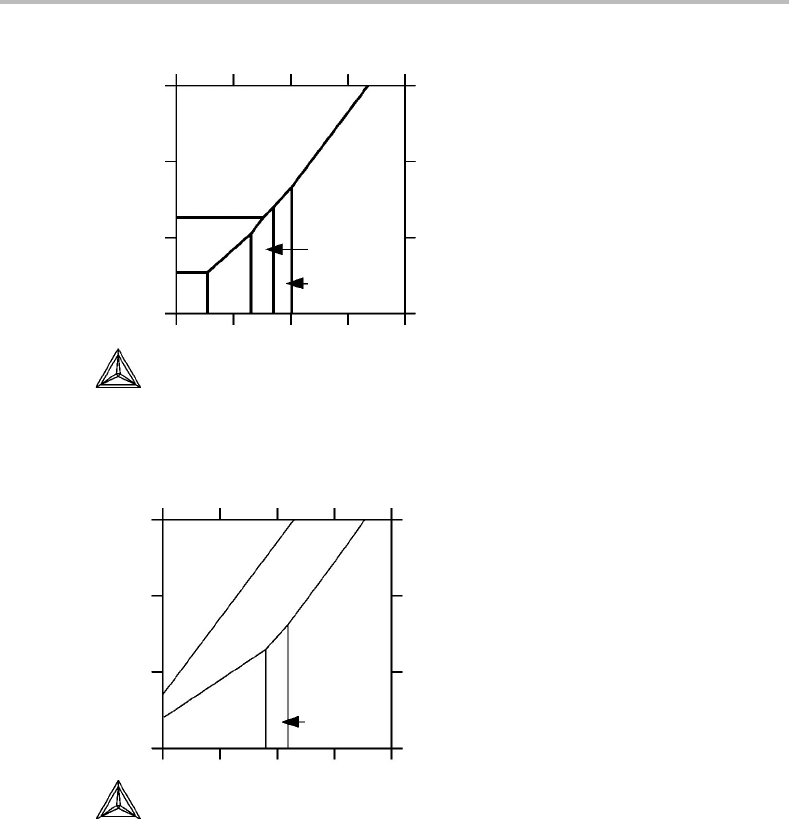
Figure 8.13 Isobaric section at 1 bar of the W–C phase diagram with two potential axes, drawn in

two alternative ways. 1/T has been plotted in the negative direction because –1/T appears

naturally as a potential in thermodynamic equations.

8.6 Binary systems

As an example of a sectioned phase diagram, Fig. 8.13 shows the bcc–W and WC phases

in the W–C phase diagram at 1 bar. Two different sets of axes are used. Since a chemical

potential has no natural zero point, a reference must be chosen. In this case graphite at

1 bar and the actual temperature was chosen for carbon.

It is interesting to note that the univariant two-phase ﬁeld approximates very well to

a straight line in Fig. 8.13(b). Its slope is obtained from the Gibbs–Duhem relation for

constant P, applied to each one of the phases. In order to calculate the slope of the line

in Fig. 8.13(b) we shall apply the Gibbs–Duhem relation in an alternative form obtained

from the ﬁfth line of Table 3.1 after dividing all the extensive quantities by N

d(µ

/T ) = H

d(1/T ) − z

d(µ

/T ) (8.25)

d(µ

/T ) = H

d(1/T ) − z

d(µ

/T ). (8.26)

On the line of coexistence the change of each potential must be the same in both phases.

We may thus eliminate d(µ

/T)bysubtracting one equation from the other, to obtain

d(µ

/T )

d(1/T )

− H

− z

. (8.27)

Here, z

= 0 and z

= 1. Since the solubility of carbon in bcc–W is very low, we can

approximate H

with the enthalpy of pure bcc–W,

bcc

,toobtain

d(µ

/T )

d(1/T )

= H

−

bcc

. (8.28)

However, in order to deﬁne a numerical value for the right-hand side, it is necessary to

choose a state of reference for carbon. By introducing graphite as the state of reference

8.6 Binary systems 171

−10

12 4

10000/T (K

−1

)

bcc

fcc

liq

bcc

(µ

−

)/RT

Figure 8.14 The Fe–C phase diagram at 1 bar, plotted with two potential axes.

for carbon, we obtain



−





d(1/T )

= H

−

bcc

−

, (8.29)

because d(

/T )/d(1/T ) =

. The right-hand side is the heat of formation of one

mole of WC units from the pure elements, a quantity we may denote by 

. The

fact that the curve in Fig. 8.13(b) is almost straight, indicates that the heat of formation

is approximately constant. By deﬁnition µ

−

is equal to RT lna

where a

is the

carbon activity, referred to graphite, and Eq. (8.29) can be written as

Rdlna

d(1/T )

= 

, (8.30)

and we could have plotted Rlna

as the abscissa and still have the almost straight line.

In Fig. 8.13(a) the potentials T and µ

−

have been used on the axes and with

the usual form of the Gibbs–Duhem relation we obtain

d(µ

−

)

=−S

bcc

= 

. (8.31)

The abscissa could have been interpreted as RTlna

.From the fact that the slope is rea-

sonably constant we may conclude that the entropy of formation of WC is approximately

constant, but not as constant as the heat of formation.

The situation will be more complicated if one or both phases can vary in composition.

As an example, a complete Fe–C phase diagram at a constant pressure is presented in

Fig. 8.14, using the axes 1/T and (µ

−

)/T . The strong curvatures are caused by

the strong variation in composition of the fcc and liquid phases. All the lines turn vertical

at low values of µ

. That is where the C content goes to zero and all phases become pure

Fe. The difference in composition thus goes to zero.

For reactions involving oxygen it is natural to use an O

gas of 1 bar as reference.

However, we may also express the oxygen potential by the ratio of the partial pressures

of CO

and CO in an ideal gas and use as a reference a gas where these partial pressures

are equal. Figure 8.15 gives an example of such a diagram with information from a large

172 Phase equilibria and potential phase diagrams

−5

10000/T (K

−1

)

681012

PbO

NiO

SnO

FeO

CO+CO

MnO

ZnO

log(P

)

Figure 8.15 Combination of isobaric phase diagrams for many M–O systems at 1 bar. The

oxygen potential is represented by P

in a hypothetical gas which is not present, except

for the line CO + CO

number of M–O systems. An oxide is stable above each line. Below the line the stable

state is either the pure metal or a lower oxide. The diagram is calculated for 1 bar and the

state for pure Zn above the boiling point is thus Zn gas of 1 bar because the O

pressure

is low enough to be neglected. This diagram is often called the Ellingham diagram. It

should be emphasized that the effect of pressure is so small that this diagram could be

used for any pressure down to zero and up to many bars, except for (i) the line CO +

which holds only for P

+ P

= 1 bar and (ii) the line for gaseous Zn.

Exercise 8.7

Consider a system with graphite in a vessel under a pressure of 1 bar and a temperature

of 1000

◦

C. The vessel can expand and accommodate a gas. What would be the partial

pressures in the gas if a small amount of oxygen is introduced?

Hint

In this case the ordinate axis in Fig. 8.15 expresses not only the oxygen potential but

also gives the actual value of P

Solution

The system would place itself on the CO + CO

line and from Fig. 8.15 we read for

1000

◦

C: log(P

) =−2which together with P

+ P

= 1 bar yields P

0.01 bar and P

= 0.99 bar.

8.7 Ternary systems 173

−2

681012

10000/T (K

−1

)

FeO

log(P

)

Figure 8.16 Solution to Exercise 8.8.

Exercise 8.8

From the information given in Fig. 8.15 construct an Fe–O potential phase diagram at a

constant pressure of 1 bar.

Hint

It is not necessary to change the axes. The liquid phase cannot be included due to lack

of information.

Solution

The phase diagram is shown in Fig. 8.16.

8.7 Ternary systems

Foraternary system one may obtain a two-dimensional phase diagram by sectioning at

constant T and P.Figure 8.17 shows such a diagram for the Ti–O–Cl system and the

axes represent µ

/RT and µ

/RT,expressed by the logarithm of the partial pressures

of O

and Cl

in an imagined ideal gas that would be in equilibrium with the system.

Again we ﬁnd that the univariant phase equilibria are represented by lines which look

straight, a fact that can again be illustrated by application of the Gibbs–Duhem relation.

For constant T and P we get by applying the Gibbs–Duhem relation in its ordinary form,

Eq. (3.84), and dividing all the extensive quantities by N

and thus introducing z

dµ

=−z

dµ

− z

dµ

(8.32)

dµ

=−z

dµ

− z

dµ

(8.33)

dµ

=−

− z

. (8.34)

174 Phase equilibria and potential phase diagrams

−5

TiCl

TiO

TiCl

TiOTi

−10

−15

−40 −30 −20

log(P

)

log(P

)

−10 0

Figure 8.17 The Ti–O–Cl phase diagram at 1 bar and 1273 K, plotted with two potential axes.

The potentials are expressed in terms of the partial pressures (in bar) in an ideal gas which is not

present.

−4

CeS

−5

−6

−7

−4 −3 −2

log(mass-% S)

log(mass-% O)

−10

Figure 8.18 The Ce–O–S phase diagram at 1 bar and 1273 K, plotted with two potential axes. The

potentials are expressed in terms of the contents in liquid iron which is not present.

It is interesting to note that the slope can be calculated directly from the compositions

involved.

A sectioned potential diagram like Fig. 8.17 is sometimes called a Kellogg diagram.

It must be emphasized that here the gas phase is not considered in the phase equilibria.

The partial pressure is simply a popular means of expressing the chemical potential of

volatile elements. It may be expressed in bar and the reference states are chosen as an

ideal gas with a partial pressure for O

or Cl

of 1 bar. Thus we have, for instance,



−

ref



RT = ln P

. (8.35)

Alternatively, one may express chemical potentials through the content in any other phase

that happens to be present or could be present. As an example, Fig. 8.18 shows a case