Hillert M. Phase Equilibria, Phase Diagrams and Phase Transformations: Their Thermodynamic Basis
Подождите немного. Документ загружается.

11.2 Calculation of allotropic phase boundaries 235
α
α
α
α
α
α
β
β
β
β
β
β
α+β
α+β
T
T
T
T
x
C
x
B
x
C
x
B
(a)
(b)
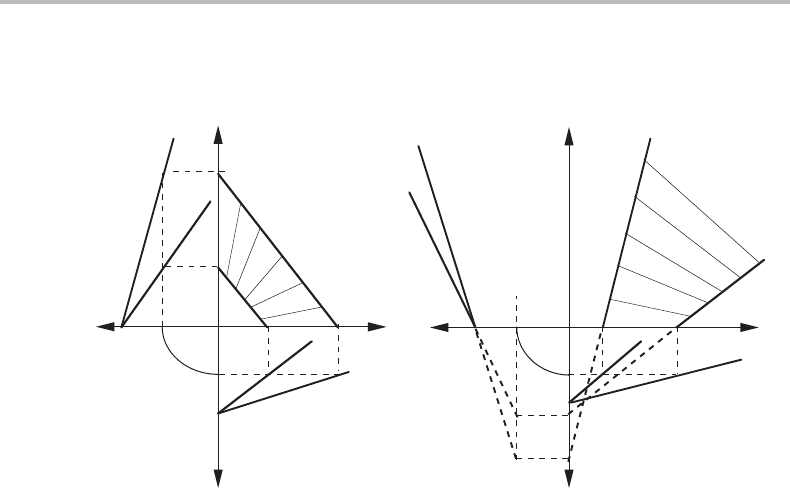
Figure 11.1 Isobarothermal section of ternary phase diagram showing equilibrium between two
phases, both with the same major component.
Solution
x
γ
j
− x
α
j
= (
o
G
γ
Fe
−
o
G
α
Fe
)/RT =−71/8.3145 · 1423 =−0.006; For the binary
Fe–Si system: −0.006 = x
γ
Si
− x
α
Si
= x
α
Si
(K
γ/α
Si
− 1) = 0.05(K
γ/α
Si
− 1); K
γ/α
Si
= 1 −
0.12 = 0.88.
ForFe–Si–Ni alloy: −0.006 = x
α
Si
(K
γ/α
Si
− 1) + x
α
Ni
(K
γ/α
Ni
− 1) = x
α
Si
· (0.88 −1) +
0.005 · (1.3 − 1) =−0.12x
α
Si
+ 0.0015; x
α
Si
= 0.0075/0.12 = 0.0625.
11.2 Calculation of allotropic phase boundaries
On an allotropic phase boundary the two phases have the same composition (see
Section 7.5). When comparing two phases we get the following expression by definition
if we apply the regular solution model to both phases (
E
G
m
= x
A
x
B
L, see Section 7.1)
because the ideal entropy term will be the same for two solution phases of the same
compositions and will thus drop out.
G
β
m
− G
α
m
= x
A
o
G
β
A
−
o
G
α
A
+ x
B
o
G
β
B
−
o
G
α
B
+ x
A
x
B
(L
β
− L
α
). (11.9)
ForlowBcontents it may be convenient to rearrange the equation as
G
β
m
− G
α
m
=
o
G
β
A
−
o
G
α
A
+ x
B
o
G
β
B
−
o
G
α
B
−
o
G
β
A
+
o
G
α
A
+ L
β
− L
α
− x
2
B
(L
β
− L
α
).
(11.10)
At sufficiently lowB contents we can neglect the last square term. Close to the temperature
236 Direction of phase boundaries
α
α
β
.
.
.
TTT
−0.01
0.01 0.01 0.02 0.01 0.0200 0
.
.
.
β
G
β
m
− G
α
m
x
B
x
C
(a) (b) (c)
o
G
β
A
−
o
G
α
A
+ 0.02∆
o
G
α
B
→βA
o
G
β
A
−
o
G
α
A
+ 0.01∆
o
G
α
B
→βA
o
G
β
A
−
o
G
α
A
+ 0.01∆
o
G
α
C
→βA
o
G
β
A
−
o
G
α
A
+ 0.02∆
o
G
α
C
→βA
o
G
β
A
−
o
G
α
A
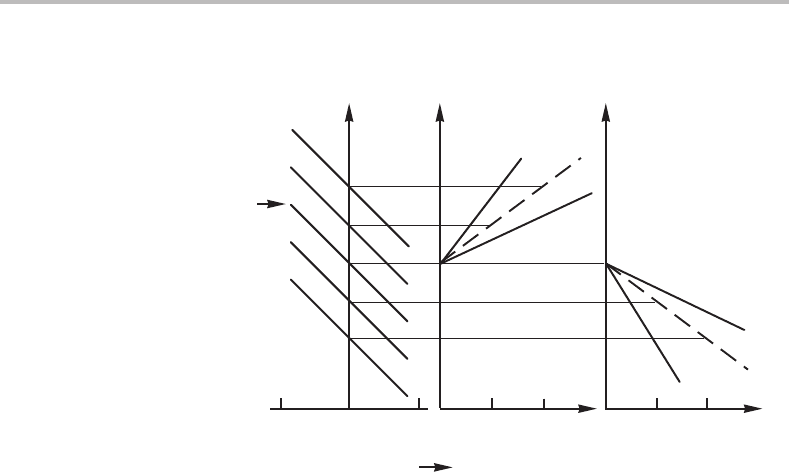
Figure 11.2 The effects of two types of alloying elements on the allotropic phase boundary.
The equilibrium phase boundaries (solid lines) fall one on each side of the allotropic phase
boundary (dashed lines). The diagrams are calculated with
o
G
α→βA
B
= RT ln 2 and
o
G
α→βA
C
=−RT ln 2.
of the allotropic phase transformation for pure A we can neglect the term
o
G
β
A
−
o
G
α
A
in
the bracket, which is there close to zero, and we thus get
G
β
m
− G
α
m
∼
=
o
G
β
A
−
o
G
α
A
+ x
B
·
o
G
α→βA
B
, (11.11)
where we have introduced the following notation
o
G
α→βA
B
=
o
G
β
B
−
o
G
α
B
+ L
β
− L
α
. (11.12)
We have already seen that the distribution coefficient of B between α and β can be
approximated by an expression for low B contents
K
α/β
B
= exp
o
G
α→βA
B
RT
= exp
o
G
β
B
−
o
G
α
B
+ L
β
− L
α
RT
. (11.13)
We thus find the following relation between the parameters used in the calculation of
allotropic boundaries as well as ordinary phase boundaries
o
G
α→βA
B
= RT ln K
α/β
B
. (11.14)
Within a narrow range of temperature and composition, it is reasonable to assume that
o
G
α→βA
B
is constant and we can then describe the effect of the alloying element as
a parallel displacement of the curve for
o
G
β
A
−
o
G
α
A
by the amount x
A
·
o
G
α→βA
B
.
We shall thus get two types of alloying effect, which are demonstrated by B and C in
Fig. 11.2. There it is assumed that
o
G
β
A
−
o
G
α
A
varies linearly with temperature.
11.2 Calculation of allotropic phase boundaries 237
α
α
γ γ
0
α
α
α
pure A
00
G
γ
m
− G
α
m
x
B
x
C
TT
T
(a)
(b)
(c)
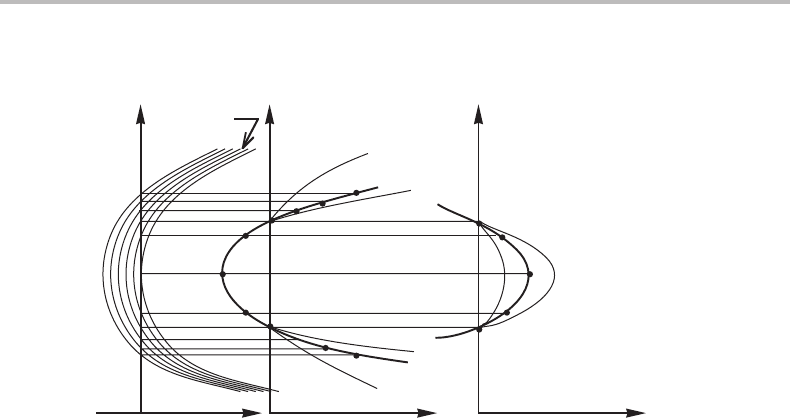
Figure 11.3 The effects of two types of alloying elements on the allotropic phase boundary (thick
lines) when the low-temperature phase comes back at high temperatures. The phase boundaries
are here given with thin lines.
We can obtain an equation for the allotropic phase boundary by inserting G
β
m
− G
α
m
=
0inEq. (11.11).
x
allot
B
=−
o
G
β
A
−
o
G
α
A
o
G
α→βA
B
=−
o
G
β
A
−
o
G
α
A
RT ln K
α/β
B
. (11.15)
Close to the transition point T
o
for pure A we obtain
x
allot
B
=−(T − T
o
)
o
H
β
A
−
o
H
α
A
T
o
o
G
α→βA
B
. (11.16)
This type of construction is especially interesting for iron because its high-temperature
phase δ is identical to its low-temperature phase α.Asaconsequence, the allotropic
phase boundary must be strongly curved as demonstrated in Fig. 11.3.Itshould be
noticed that one can extrapolate all phase boundaries mathematically, even to negative
alloy contents if one avoids the use of mathematical expressions containing lnx
B
. The
two types of alloying effects on iron, the stabilization of austenite (γ)byelement B and
ferrite (α)byelement C, thus look like each other’s mirror images. It should finally be
emphasized that the approximate equations derived in this section are valid only up to a
few atomic per cent of the alloying element.
Exercise 11.2
Suppose pure A has an α/β transition at 1000 K. An alloying element B, which itself
has the α structure at all temperatures, has been found first to expand the range of the
β phase to lower temperatures but at higher B contents the α phase will win. Find
the congruent point for the α/β equilibrium from the following kind of expression for

238 Direction of phase boundaries
both phases: G
m
= x
o
A
G
A
+ x
o
B
G
B
+ RT(x
A
lnx
A
+ x
B
lnx
B
) + Lx
A
x
B
,where
o
G
α
A
−
o
G
β
A
= R(T − 1000);
o
G
α
B
−
o
G
β
B
=−RT; L
α
= 200R and L
β
=−1000R.
Hint
At a point of extremum, where the ordinary phase boundaries are horizontal, the allotropic
phase boundary coincides with them and is also horizontal. It is much easier to calculate
this point from the allotropic phase boundary than from the ordinary ones. It is given by
G
α
m
− G
β
m
= 0.
Solution
G
α
m
−G
β
m
=x
A
(
o
G
α
A
−
o
G
β
A
) +x
B
(
o
G
α
B
−
o
G
β
B
) +(L
α
− L
β
)x
A
x
B
; x
A
R(T −1000) +
x
B
(−RT) + (200 + 1000)Rx
A
x
B
= 0; RT(x
A
− x
B
) − 1000Rx
A
+ 1200Rx
A
x
B
=
0; T = (1000x
A
− 1200x
A
x
B
)/(x
A
− x
B
) = 1000(1 − 2.2x
B
+ 1.2x
2
B
)/(1 − 2x
B
);
dT /dx
B
= 1000[(1 − 2x
B
)(−2.2 + 2.4x
B
) − (1 − 2.2x
B
+ 1.2x
2
B
)(−2)]/(1 − 2x
B
)
2
=
0; x
B
= 0.092; T = 990K.
11.3 Variation of a chemical potential in a two-phase field
We shall now consider the effect of a ternary alloying addition on a two-phase equilibrium
which exists already in a binary system. The effect of the minor binary component on the
chemical potential can be estimated rather accurately from the distribution coefficient
of the alloying element between the two phases without using any information on the
direction of the phase boundaries in the ternary system. In Section 8.8 we considered the
effect of any small change in composition of phases in a ternary system by combining
two Gibbs–Duhem relations at constant T and P.Wecan easily introduce a distribution
coefficient in Eq. (8.46).
dµ
C
=−
x
α
B
x
β
A
− x
β
B
x
α
A
x
β
A
x
α
C
− x
α
A
x
β
C
· dµ
B
= x
α
B
x
β
A
·
1 − K
β/α
BA
x
α
A
x
β
C
− x
β
A
x
α
C
· dµ
B
. (11.17)
By dividing through with (x
α
A
+ x
α
B
) · (x
β
A
+ x
β
B
), which is equal to 1, we can change
from the x composition to u (see Section 4.3). The distribution coefficient for B and A
between the two phases can be defined with both types of variable
K
β/α
BA
= x
β
B
x
α
A
x
β
A
x
α
B
= u
β
B
u
α
A
u
β
A
u
α
B
. (11.18)
At low contents of B in both phases we can approximate u
α
A
and u
β
A
with unity and we
can apply Henry’s law to B in the α phase in the following form if the C content in α is
also low,
µ
B
= G
α
B
=
o
G
α
B
+ RT ln f
α
B
+ RT ln u
α
B
(11.19)
dµ
B
=
RT
u
α
B
· du
α
B
. (11.20)
11.3 Variation of a chemical potential in a two-phase field 239
α
α+β
β
α+β
α
β
u
M
u
C
u
C
u
M
a
c
decreases a
c
increases
(a) (b)
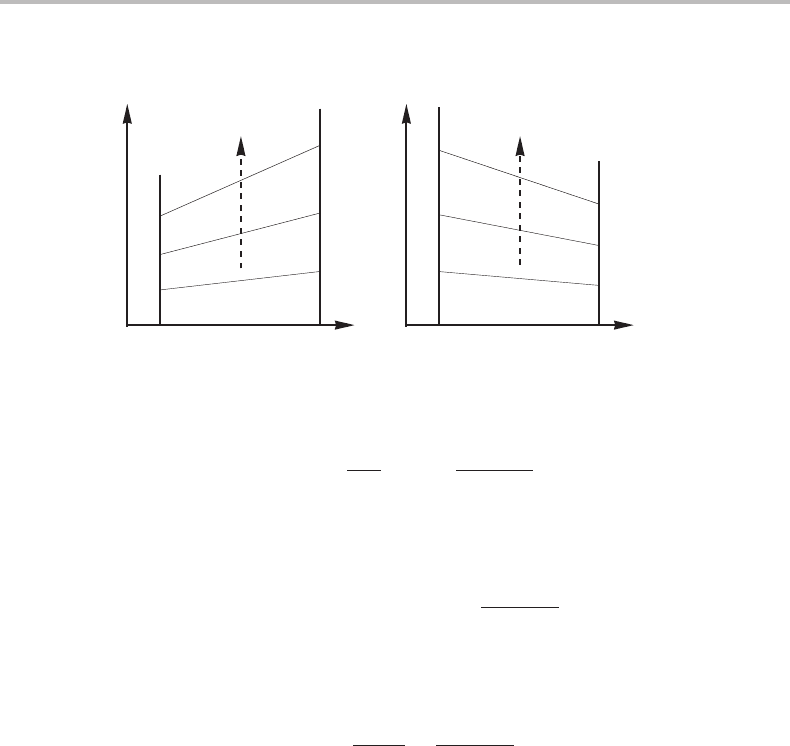
Figure 11.4 The effect of the slope of tie-lines on the activity of a component in a two-phase field.
The equation is thus simplified to
dµ
C
du
α
B
= RT ·
1 − K
β/α
BA
u
β
C
− u
α
C
. (11.21)
By approximating the right-hand side with its value close to the binary A–C side of the
system, we can easily integrate and obtain
µ
ternary
C
− µ
binary
C
= RT ·
1 − K
β/α
BA
u
β
C
− u
α
C
· u
α
B
, (11.22)
where u
α
B
is the B content of α in the ternary alloy. By introducing the activity for C we
instead obtain
ln
a
ternary
C
a
binary
C
=
1 − K
β/α
BA
u
β
C
− u
α
C
· u
α
B
. (11.23)
This is a useful equation for rough calculations. It demonstrates that an alloying element
which concentrates to the phase which is richest in C, i.e. which has K
β/α
BA
> 1ifβ is
the C-rich phase, will decrease the C activity for the two-phase equilibrium α + β.An
alloying element that concentrates to the C-poor phase will increase the C activity. From
the derivation it is evident that this effect is additive for several alloying elements if
evaluated for µ
C
or lna
C
.
The value of K
β/α
BA
is directly related to the slope of the tie-lines in the u
C
, u
M
phase diagram. We can thus illustrate the two cases with the phase diagrams in
Fig. 11.4 where the u parameters are used. The alloying element will have no effect on
the C activity of the two-phase equilibrium if the tie-lines are horizontal, i.e. if they are
directed towards the C corner which is situated infinitely far away in a diagram with the u
variable.
The equation shows that µ
C
does not change in a two-phase field where K = 1, i.e.
where the two phases have the same content of B relative to A. This is thus a point
of extremum and the present result is in complete agreement with Konovalov’s rule.
Compare with Exercise 10.11 where N plays the role of C and Cr the role of B.

240 Direction of phase boundaries
The chemical potential of a two-phase equilibrium can also be strongly affected by
a difference in pressure, caused by the surface energy in a curved phase interface. The
complete form of the Gibbs–Duhem equation is the following:
x
A
dµ
A
+ x
B
dµ
B
+ x
C
dµ
C
= V
m
dP − S
m
dT . (11.24)
Now we shall let the pressure vary in the β phase but keep the temperature constant.
Equation (11.17) will thus have one more term, which can be written as
x
α
A
V
β
m
dP
β
x
α
A
x
β
C
− x
β
A
x
α
C
or
u
α
A
dP
β
u
α
A
u
β
C
− u
β
A
u
α
C
·
V
β
m
1 − x
β
C
. (11.25)
ForlowBcontents we can thus write
dµ
C
= k · dµ
α
B
+l · dP
β
, (11.26)
where k = RT(1 − K
β/α
BA
)/(u
β
C
− u
α
C
) and l = V
β
m
/(1 − x
β
C
)(u
β
C
− u
α
C
).
Exercise 11.3
Low-carbon steels are sometimes carburized in order to increase the surface hardness.
This is done at a temperature where γ(fcc) is the stable phase. A hard and brittle carbide
called cementite, Fe
3
C, may form if one uses a high carbon activity in the gas. In the
binary system it has a carbon activity of 1.04 when in equilibrium with γ at 1173 K.
What would be the highest carbon activity to be used if one wants to avoid cementite for
a steel with 1.5 atom % Cr and 3 atom % Ni. They can both replace Fe in cementite and
the distribution coefficient K
cementite/γ
MFe
is 6 for Cr and 0.1 for Ni.
Hint
The effects of two alloying elements on µ
C
or lna
C
are additive. The alloy contents given
are for the initial low-carbon steel and we should evaluate the u variable because it does
not change when C is added due to its definition. We obtain u
γ
Cr
= 0.015 and u
γ
Ni
= 0.03.
For cementite u
C
= 1/3 and for γ in equilibrium with cementite at 1173 K we have 1.23
mass%Cwhich gives u
C
= 0.059.
Solution
ln(a
alloy
C
/a
binary
C
) = [(1 − 6) · 0.015 + (1 − 0.1) ·0.03]/[(1/3) − 0.059] =−0.17;
a
alloy
C
= a
binary
C
· exp(−0.17) = 1.04 · 0.84 = 0.88. This is the highest value one should
use.
11.4 Direction of phase boundaries
So far, we have discussed the direction of phase boundaries in some simple cases. For
the general case we need a more powerful method and we should then turn to the Gibbs–
Duhem relation. In fact, we have already calculated the directions of phase fields in

11.4 Direction of phase boundaries 241
potential phase diagrams by the application of the Gibbs–Duhem relation. However, in
order to calculate the directions of the phase boundaries in molar phase diagrams we
must introduce the molar quantities instead of the potentials as variables in the Gibbs–
Duhem relation. No general treatment can be given here in view of the large variety that
can occur in mixed phase diagrams. Only the special case will be treated where T and P
are retained but all the chemical potentials are replaced by molar contents.
The fact that the molar quantities of two phases in equilibrium are generally different,
although the potentials are equal, makes it necessary to choose one of the phases, for
instance α, and express the potentials through its molar quantities. If T and P are retained,
then it is convenient to express the changes of the chemical potentials µ
i
through the
composition dependence of the partial Gibbs energies in the α phase, G
α
i
.Inorder to
make the enthalpy appear in the final expression instead of the entropy we shall use
the potentials occurring in the special form of the Gibbs–Duhem relation containing
enthalpy. It is obtained from the fifth line in Table 3.1.
H
β
m
d(1/T ) +
V
β
m
T
dP −
c
i=1
x
β
i
d(µ
i
/T ) = 0. (11.27)
We shall now introduce the properties of the chosen phase α by using µ
i
= G
α
i
and
with 1/T, P and x
α
j
for j > 1asthe independent variables, treating x
α
1
as the dependent
composition variable. We can then eliminate d(µ
i
/T) using
d(µ
i
/T ) =
∂G
α
i
∂(1/T )
d(1/T ) +
∂G
α
i
∂ P
dP/T +
c
j=2
∂G
α
i
∂x
α
j
dx
α
j
T . (11.28)
We can insert
∂
G
α
i
T
∂(1/T ) = H
α
i
(11.29)
∂G
α
i
∂ P = V
α
i
. (11.30)
Applying Eq. (4.7)tothe Gibbs energy we obtain by selecting component 1 as the
dependent one,
G
α
i
= G
α
m
+ ∂G
α
m
∂x
α
i
−
c
l=2
x
α
l
∂G
α
m
∂x
α
l
. (11.31)
Using the notation of second derivatives of G
m
when component 1 is the dependent one,
which was introduced in Section 6.6,weobtain,
∂G
α
i
∂x
α
j
= g
α
ij
−
c
l=2
x
α
l
g
α
jl
. (11.32)
It should be noted that g
α
1 j
does not exist since component 1 is the dependent one. When
inserting these expressions in Eq. (11.27)weshall also replace H
β
m
by x
β
i
H
β
i
and V
β
m
by x
β
i
V
β
i
.
x
β
i
H
β
i
d(1/T ) +
x
β
i
V
β
i
dP/T
−
x
β
i
H
α
i
d(1/T ) + V
α
i
dP/T +
c
j=2
g
α
ij
−
c
l=2
x
α
l
g
α
jl
dx
α
j
/T
= 0. (11.33)

242 Direction of phase boundaries
However,
c
i=1
x
β
i
g
α
ij
−
c
l=2
x
α
l
g
α
jl
=
c
i=2
x
β
i
g
α
ji
− 1 ·
c
l=2
x
α
l
g
α
jl
=
c
i=2
x
β
i
− x
α
i
g
α
ji
,
(11.34)
since g
ij
for i = 1 does not exist and the terms in the summation over index l are
independent of index i.Weobtain, because d(1/T ) =−dT /T
2
c
i=2
c
j=2
x
β
i
− x
α
i
g
α
ji
dx
α
j
+
c
i=1
x
β
i
H
β
i
− H
α
i
dT /T −
c
i=1
x
β
i
V
β
i
− V
α
i
dP = 0.
(11.35)
This is the desired relation. Contrary to the Gibbs–Duhem relation this equation always
concerns two phases, and all the terms become zero when applied to the phase which was
chosen for expressing the chemical potentials. When applied to more than two phases it
yields a system of equations and some variables can then be eliminated with the method
used for calculating the direction of phase fields from the Gibbs–Duhem relation. The
elements of the determinants will then be (x
β
i
− x
α
i
)g
α
ij
instead of x
β
i
.However,we
shall apply the equation to equilibria concerning two coexisting phases and the equation
can then be applied directly.
Forabinary system under isobaric conditions we get for the phase boundaries
∂x
α
2
∂T
coex
=
x
β
i
H
α
1
− H
β
1
+ x
β
2
H
α
2
− H
β
2
x
β
2
− x
α
2
g
α
22
T
=
H
βinα
m
x
β
2
− x
α
2
g
α
22
T
(11.36)
∂x
β
2
∂T
coex
=
x
α
i
H
β
1
− H
α
1
+ x
α
2
H
β
2
− H
α
2
x
α
2
− x
β
2
g
β
22
T
=
H
αinβ
m
x
α
2
− x
β
2
g
β
22
T
(11.37)
The numerator is equal to the heat of solution of the other phase (α or β)inthe phase
being considered (β or α). The phase boundary will be vertical if the heat of solution is
zero. Figure 11.3(c) shows a case where both boundaries turn vertical at almost the same
temperature and then lean the other way. Both phases were rich in one component,1, and
the heat of solution mainly depended on the terms with (H
α
1
− H
β
1
), a quantity that went
through zero in that temperature range.
Either of these two equations can be used to evaluate the slope of a phase boundary
but also to calculate the width of a two-phase field if the slope is known.
x
β
2
− x
α
2
=
H
βinα
m
g
α
22
T
dx
α
2
dT
coex
=−
H
αinβ
m
g
β
22
T
dx
β
2
dT
coex
. (11.38)
Exercise 11.4
Derive an equation for the solubility of pure component 2 in a phase α which is almost
pure component 1.

11.4 Direction of phase boundaries 243
Hint
Section 7.1 gives g
α
22
≡ d
2
G
α
m
/d(x
α
2
)
2
∼
=
RT/x
α
2
if x
α
2
is small. Also use x
β
2
− x
α
2
∼
=
1.
Solution
dx
α
2
/dT = H
m
/(RT
2
/x
α
2
); d(ln x
α
2
)/d(1/T ) = H
m
/R; x
α
2
= K · exp(H
m
/RT).
Usually, H
m
is replaced by −L,where L is the heat given off by the dissolution
of β.
Exercise 11.5
Apply Eq. (11.35)toabinary case at constant P. Then consider the α/α + β phase
boundary in the T, x phase diagram in a system where α is almost pure A and β is a bcc
phase close to the 50–50 composition. Suppose β has a sharp transformation at T
o
from
a perfectly ordered to a perfectly disordered state (which would never happen). Calculate
the angle of the α/(α + β) phase boundary at T
o
(or, more precisely, the difference in
direction, dx/dT,ofthis phase boundary just below and just above T
o
).
Hint
At constant P:[x
β
i
(H
α
1
− H
β
1
) + x
β
2
(H
α
2
− H
β
2
)]dT = (x
β
2
− x
α
2
)g
α
22
T dx
α
2
. Notice that
x
β
1
H
β
1
+ x
β
2
H
β
2
= H
β
m
and that the entropy of disordering is −R(x
1
ln x
1
+ x
2
ln x
2
) =
R ln 2 for x
1
= x
2
= 0.5. For the dilute solution of component 2 in α we may use g
α
22
=
RT/x
α
1
x
α
2
.
Solution
x
β
1
= x
β
2
= 0.5gives dx
α
2
/dT = 0.5(H
α
1
− H
β
1
+ H
α
2
− H
β
2
)/(0.5 − 0)g
α
22
T .Bytak-
ing the difference between just below and just above the transition, we eliminate H
α
1
and H
α
2
and thus get (dx
α
2
/dT ) = (H
β
m
− H
β
m
)/0.5g
α
22
T
o
. But H
β
m
− H
β
m
= H
ordering
m
and at the transition point the two states have the same Gibbs energy and thus
H
ord
m
− T
o
S
ord
m
= 0; (dx
α
2
/dT ) = T
o
S
ord
m
/0.5g
α
22
T
o
= R ln 2/(0.5RT
o
/x
α
2
) =
2x
α
2
ln 2/T
o
.
Exercise 11.6
When adding a third component C to a certain binary system A–B under constant P,
one found that the depression of the freezing point of a stoichiometric phase A
a
B
b
only
depended upon the molar content x
C
and was independent of whether one kept x
A
, x
B
or
x
A
/x
B
constant. Examine if this result can be expected in general. Suppose the pressure
is constant.

244 Direction of phase boundaries
Hint
Apply the general equation for the direction of phase boundaries, Eq. (11.35), to the
ternary case, making C the dependent component 1. Remember that g
2
is the deriva-
tive of G
m
with respect to x
2
,keeping x
3
constant, i.e. with dx
1
=−dx
2
. Writing G
m
as x
i
(
o
G
i
+ RT ln x
i
) +
E
G
m
(x
2
, x
3
)weget: g
2
=
o
G
2
−
o
G
1
+ RT(ln x
2
− ln x
1
) +
∂
E
G
m
/∂x
2
and g
22
= RT(1/x
2
+ 1/x
1
) + ∂
2E
G
m
/∂x
2
2
, etc. Look for the predominating
term when x
1
is small. Furthermore, the liquid composition is close to that of A
a
B
b
.
Solution
For x
C
≡ x
1
→ 0weget [(x
β
2
− x
L
2
)g
L
22
+ (x
β
3
− x
L
3
)g
L
23
]dx
L
2
+ [(x
β
2
− x
L
2
)g
L
32
+ (x
β
3
−
x
L
3
)g
L
33
]dx
L
3
=−[x
L
2
(H
β
2
− H
L
2
) + x
L
3
(H
β
3
− H
L
3
)]dT /T under constant P. The pre-
dominating term in g
22
is RT/x
1
and all the other second derivatives of g have the same
predominating term. By neglecting other terms we get [(x
β
2
− x
L
2
+ x
β
3
− x
L
3
) · RT/x
L
1
]
dx
L
2
+ [(x
β
2
− x
L
2
+ x
β
3
− x
L
3
) · RT/x
L
1
]dx
L
3
= [(x
β
2
− x
L
2
+ x
β
3
− x
L
3
) · RT/x
L
1
](dx
L
2
+
dx
L
3
) =−[x
L
2
(H
β
2
− H
L
2
) + x
L
3
(H
β
3
− H
L
3
)]dT /T . The depression of the freezing point
thus depends on dx
L
2
+ dx
L
3
which is equal to −dx
L
C
whether one keeps x
A
, x
B
or x
A
/x
B
constant.
11.5 Congruent melting points
It is immediately clear from our equations for dx/dT that for a congruent transformation
point in a binary system, e.g. for x
β
2
= x
L
2
, the phase boundaries must be horizontal and
such a point must be a point of temperature extremum. This is also in agreement with
Konovalov’s rule (see also [22]). However, at the side of the system where x
L
2
approaches
zero, g
L
22
approaches infinity as RT/x
L
2
and the whole denominator in Eq. (11.37), with L
instead of β, approaches RT
2
(x
α
2
/x
L
2
− 1) which is not zero. Thus, the phase boundaries
do not turn horizontal on the sides of the system. The two cases are demonstrated in
Fig. 11.5.
The slopes of the phase boundaries at the left-hand side of the binary system in
Fig. 11.5 can be evaluated from the limiting value of g
α
22
which is RT/x
α
2
when x
α
2
→ 0
(see Section 7.1).
∂x
α
2
∂T
coex
=
1
x
β
2
− x
α
2
·
o
H
α
1
−
o
H
β
1
RT/x
α
2
T
=
K
α/β
2
1 − K
α/β
2
·
o
H
α
1
−
o
H
β
1
RT
2
(11.39)
∂x
β
2
∂T
coex
=
1
x
α
2
− x
β
2
·
o
H
β
1
−
o
H
α
1
RT/x
β
2
T
=
1
1 − K
α/β
2
·
o
H
α
1
−
o
H
β
1
RT
2
. (11.40)
The width of the two-phase field at some temperature T below the transformation point
T
o
for pure component 1 is obtained from the difference,
o
H
β
1
−
o
H
α
1
RT
2
=
∂
x
β
2
− x
α
2
∂T
∼
=
x
β
2
− x
α
2
T
o
− T
. (11.41)
