Heubach S., Mansour T. Combinatorics of Compositions and Words

Подождите немного. Документ загружается.

Automata and Generating Trees 275

 = 2, that is, avoidance of the pattern τ = 123 via a combinatorial proof. It

should be clear from the correspondence in Theorem 7.51 and Example 7.53

that the simple paths of length r in A(τ



,k+ ) are in one-to-one correspon-

dence with tableaux T of the following type:

(1) T is weakly increasing in rows and columns.

(2) No integer appears in more than one row.

(3) The entries of T are exactly [r].

(4) The shape of T is contained in λ

,k

Before giving the result on AW

123

[k]

(n) we need some notation.

Deﬁnition 7.55 A Young tableau that satisﬁes Properties (1) and (2) above

is called a segmented tableau, and we denote the number of segmented tableaux

satisfying properties (3) and (4) by a(, k, r). A segmented tableau of size

[] × [k] is called primitive if all columns are diﬀerent (that is, every pair

of columns diﬀers in at least one entry). We denote the set of primitive

segmented tableaux of size [] × [i] with r diﬀerent entries by PR

,i,r

,andlet

pr(, i, r)=|PR

,i,r

With these deﬁnitions, we can obtain an explicit formula for AW



[k+]

(n)in

terms of pr(, i, r) which can be computed for special cases.

Proposition 7.56 The number of words of length n on the alphabet [k + ]

that avoid the increasing pattern τ



=12···( +1) is given by



[k+]

(n)=

k



r=0



i=0



n−r

pr(, i, r)







. (7.4)

Proof Since the number of words of length n on [k + ] avoiding τ



is the

same as the number of paths of length n in the automaton, we can count

the number of words that avoid an increasing pattern τ



via the paths in the

automaton. All such paths are loop paths that can be counted via the simple

paths. Select the r vertices that deﬁne the simple path, which can be done in





ways. Since the total length is n, there have to be n −r loops. At each of

the vertices, there are  loops to choose from. Because of the structure of the

loop paths, selecting m

loops at the i-th vertex in the path results in a total

of 

+···+m

= 

n−r

choices. Finally, the simple paths are in one-to-one

correspondence to primitive segmented tableaux, and therefore



[k+]

(n)=

k



r=0



n−r

a(, k, r)





. (7.5)

276 Combinatorics of Compositions and Words

Next, we can create the segmented tableau of size [] × [k] satisfying proper-

ties (3) and (4) that have i diﬀerent columns from the primitive segmented

tableaux in PR

,i,r

by inserting α

copies of the ﬁrst column to the left of the

ﬁrst column, α

copies of the second column between the ﬁrst and the second

column, and so on. After the i-thcolumnwemayinsertα

i+1

columns of all

blanks, requiring that

+ α

+ ···+ α

i+1

= k − i.

This process can be done in





ways, and therefore, we can express the

number of segmented tableaux in terms of the number of primitive segmented

tableaux as

a(, k, r)=



i=0

pr(, i, r)





which gives (7.4). 2

Note that the function a(, k, r) is actually a polynomial in k of degree r

due to the creation of the segmented tableaux from the primitive segmented

tableaux. The numbers pr(, i, r) are generally hard to compute, but there are

two special cases in which we can obtain nice results, namely pr(, n, n)and

pr(2,i,r). The latter expression will help us give the promised combinatorial

proof for a closed formula for AW

123

[k]

(n). We start by deriving pr(, n, n).

Theorem 7.57 There is a bijection between the permutations of n avoiding



and the primitive segmented tableaux of size []×[n] with n diﬀerent entries,

that is,

pr(, n, n)=|S

(τ



)|.

Proof We will deﬁne a bijection between S

(τ



)and∪



m=0

m,n,n

such

that the height m of the tableau corresponds to the greatest increasing sub-

sequence in a given permutation (thus, m ≤ ). With r

(v) as deﬁned in

the proof of Lemma 7.40, let r(v)=(r

(v),r

(v),...,r

(v)), where m is the

length of the longest increasing subsequence in v. Finally, assume that k is

large enough so that all increasing subsequences in permutations in S

(τ



)are

considered extendible.

Now if π = π

···π

is any permutation in S

(τ



), deﬁne a tableau T =

T (π)asfollows. LettheﬁrstcolumnofT be r(π), the second column be

r(π

···π

n−1

), and so on. For example, for the permutation 351462, the ﬁrst

column has entries 1, 2, and 6, since the smallest end value for increasing

subsequences of length one is 1, for those of length two it is 2 (from the

subsequence π

), and for length three it is 6 (from either the subsequence

or the subsequence π

). In the same manner, we obtain the

Automata and Generating Trees 277

remaining ﬁve columns and

T (351462) =

1 1 1 1 3 3

2 4 4 5 5

6 6

For each new column, one of two things happens: either the value that was

removed from consideration was a smallest end value of the increasing subse-

quences of length s, and therefore the respective value will increase if there is

still an increasing subsequence of that length; or, if the removed value came

from the only subsequence of length s in the previous step, then the entry in

row s will be empty for the current (and any subsequent) column. Thus, there

is exactly one value that is diﬀerent in adjacent columns. By construction, we

have that T (π) ∈∪



m=0

m,n,n

. Moreover, from Lemma 7.40 we get that a

tableau T is the image of some S

(τ



) if and only if the following are all true:

(a) T has n columns and entries 1, 2,...,n.

(b)LetT

denote the i-th column. If i<jthen T

is smaller than T

component-wise order. (If T

and T

have diﬀerent size ﬁll the empty

slots of T

with n +1).

from T

i+1

to T

, that is, when scanning the columns from right to left.

Furthermore, if T ∈∪



m=0

m,n,n

, then conditions (a) and (b) are trivially

satisﬁed. At least one new entry appears every time we move from T

i+1

, because otherwise T

= T

i+1

and T fails to be primitive. On the other

hand, if more than one new entry appears in a transition, then in some later

transition there cannot appear a new entry, since T has n columns and n

distinct entries. This veriﬁes condition (c) and gives the statement. 2

From Theorem 7.57 we obtain as a special case that

pr(2,n,n)=|S

(123)| = C

n +1





the n-th Catalan number, which was originally shown by Knuth [122]. We

now look at a more general case, the enumeration of pr(2,i,r), where we also

obtain a connection to the ubiquitous Catalan numbers.

Theorem 7.58 The number of primitive segmented tableaux of size 2×i with

r diﬀerent entries is given by

pr(2,i,r)=

i +1





r − i



= C



r − i



where C

is the i-th Catalan number.

278 Combinatorics of Compositions and Words

Before we give a proof of Theorem 7.58 we will need some deﬁnitions and a

lemma. Let PR

(2,s,r) be the set of tableaux in PR(2,s,r)thatcompletely

ﬁll the shape [2] × [s], and let pr

(2,s,r)=|PR

(2,s,r)|.Then

pr(2,s,r)=pr

(2,s,r)+pr

(2,s,r+1),

since we can obtain the tableaux with r entries that are not completely ﬁlled

from the completely ﬁlled ones with r + 1 entries by deleting all entries r +1.

To prove the theorem we will show that

(2,s,r)=



s − 1

2s − r



where C

is the s-th Catalan number.

Deﬁnition 7.59 Two arrays A and B are said to be order-equivalent if A

≤



if and only if B

≤ B



for all i, j, i



We ﬁrst deﬁne an operation + that takes tableaux with r diﬀerent entries to

tableaux with r +1 diﬀerent entries. Let T ∈PR

(2,s,r). Suppose that j is

an index such that T

= T

i(j+1)

for either i =1ori =2. WriteT as T = LR,

where L consists of the ﬁrst j columns and R consists of the remaining s − j

columns. Let R



be the array that is order-equivalent to R with entries from

the set { distinct entries in R}∪{r +1}−{T

i(j+1)

}. Order-equivalence will

then dictate which element (if any) must occur more than once. We deﬁne

T + j to be the tableau LR



. For example, let

T =

1 2 4 4

3 5 5 6

Then there are two such indices, namely j =2(sinceT

= T

)andj =3

(since T

= T

). For j =2,R



has entries {4, 5, 6}∪{7}−{5} = {4, 6, 7}.

Since the smallest element in R occurs twice, so the smallest element in R



has to occur twice. Therefore,

T +2=

1 2 4 4

3 5 6 7

Note also that T ∈PR

(2,s,r) has exactly 2s cells. Once we have placed the

r distinct values, then there are 2s − r cells where a newly placed value can

lead to an equality of adjacent cells. Thus there are 2s −r pairs i and j with

j ∈ [s − 1] and i =1ori =2suchthatT

= T

i(j+1)

.LetS = {s

···<s

} be the set of these indices for j (since we can have equality in only

one of the two rows) and deﬁne a function Φ

: PR

(2,s,r) →ST

2,s

(T )=(···((T + s

)+s

t−1

)+···+ s

Automata and Generating Trees 279

where ST

2,s

is the set of standard tableaux of shape [2] ×[s]andΦ

consists

of applying the operation + a total of t times, starting with the tableau T

and iteratively adding the elements in S from right to left. The fact that Φ is

a bijection will prove the theorem, because |ST

2,s

| = C

(see [183, Exercise

6.19 (ww)]). To ﬁnd the inverse of Φ we need to deﬁne an inverse operation

to +.

Let T ∈PR

(2,s,r)and1≤ b ≤ s − 1 be such that T

1(b+1)

and

2(b+1)

(because this is the situation produced by +). Deﬁne two arrays

T |

and T |

as follows. For T = LR,whereL consists of the ﬁrst b columns

and R of the s − b last columns of T , deﬁne T |

= LR



to be the array

where R



is the unique array order-equivalent to R with entries from the set

{distinct entries in R}∪{T

}−{r}. Similarly, let T |

= LR



be the array

where R



is the unique array order-equivalent to R with entries from the set

{distinct entries in R}∪{T

}−{r}.Forb =2,

1 2 4 4

3 5 6 7

(

1 2 2 2

3 5 4 6

1 2 4 4

3 5 6 7

(

1 2 4 4

3 5 5 6

Note that exactly one of T |

and T |

is a primitive segmented tableau. This

is no accident.

Lemma 7.60 Let T ∈PR

(2,s,r) and 1 ≤ b ≤ s − 1 be such that T

1(b+1)

and T

2(b+1)

.Then

T |

∈PR

(2,s,r− 1) ⇔ T |

/∈PR

(2,s,r− 1)

⇔ T

2(b+1)

= T

+1.

Moreover, if A = T |

∈PR

(2,s,r − 1),thenA

= A

2(b+1)

,andifB =

T |

∈PR

(2,s,r− 1),thenB

= B

1(b+1)

Proof Let A = T |

. All entries in T that are smaller than T

will be

mapped onto themselves, and A

= T

− 1forA

. This is the case

because all values in the set {T

+1,T

+2,...,r} have to occur to the right

of T

by construction of the map Φ. Therefore, A ∈PR

(2,s,r− 1) if and

only if T

2(b+1)

= T

+ 1 (since otherwise the entry T

will appear in both

the ﬁrst and the second row). Now we look at B = T |

.Fori ≥ 1, let y

the entries in T satisfying T

≤ T

2(b+1)

ordered by size. Then the entry

will be mapped to an element smaller than T

and y

will be mapped to

i−1

for i>1. Thus B ∈PR

(2,s,r− 1) if and only if T

2(b+1)

as claimed. The last statement of the lemma follows from the arguments just

given. 2

We are now ready to give a proof of Theorem 7.58.

280 Combinatorics of Compositions and Words

Proof of Theorem 7.58 If T ∈PR

(2,s,r)and1≤ b ≤ s − 1aresuch

that T

1(b+1)

and T

2(b+1)

, we deﬁne T − b to be the array T |

T |

that is in PR

(2,s,r− 1). By Lemma 7.60 we have that

(T + j) −j = T if T

= T

i(j+1)

for either i =1ori =2,

(T − j)+j = T if T

i(j+1)

for both i =1, 2. (7.6)

Now, for S = {s

< ···<s

} with t =2s − r and P ∈ST

2,s

, we deﬁne

Ψ(S, P )=P − s

− s

−···−s

It follows from (7.6) that Ψ is the inverse to Φ and therefore Theorem 7.58

follows. 2

Putting all the pieces together results in a combinatorial proof of the closed

form for the number of words that avoid the subsequence pattern 123, which is

diﬀerent, but of course equivalent to the formula proved originally by Burstein

[31] using a noncombinatorial argument (see Theorem 7.61). Note that the

result of Theorem 7.61 applies to all permutation patterns τ ∈S

(since we

have shown in Section 6.3 that all subsequence permutation patterns of length

three are equivalent).

Theorem 7.61 For al l n, k ≥ 0 we have that

123

[k+2]

(n)=



r=0



i=0

n−r



r − i





where C

i+1





is the i-th Catalan number. Moreover, the generating

function F

123

(x, y)=



n,k≥0

123

[k+2]

(n)x

is given by

123

(x, y)=

(1 − y)(1 −2x)



xy(1 − x)

(1 − y)(1 −2x)



where C(x) is the generating function for the Catalan numbers. Equivalently,

123

(x, y) is algebraic and satisﬁes the equation:

xy(1 − y)(1 − x)F

− (1 − y)(1 − 2x)F +1=0.

Proof The formula for AW

123

[k+]

(n) follows immediately from Proposition

7.56 and Theorem 7.58. The result for the generating function is obtained by

using the result of [31] for the generating function AW

123

[k]

(x, y), adjusted for

the shift in the sequence AW

123

[k+2]

(n). 2

We close this section with a result on the sequence {AW

[n]

(n)}

n≥0

.For

permutation patterns τ , the study of S

(τ) has been an area of very active

Automata and Generating Trees 281

research. Since S

(τ) ⊂AW

[n]

(τ), the sequence {AW

[n]

(n)}

n≥0

is a natural

extension and of particular interest. Typical questions posed involve ﬁnding

an explicit formula for the number of words of length n on the alphabet [n]

avoiding a given pattern. If we are only able to derive an expression for the

generating function, then typical questions concern the type of generating

function for {AW

[n]

(n)}

n≥0

. We can give a partial answer for patterns from

. To do so, we need the following deﬁnition.

Deﬁnition 7.62 Asequence{f (n)} is polynomially recursive (or P-recurs-

ive) if there are a ﬁnite number of polynomials p

(n) such that



i=0

(n)f(n + i)=0,

for all integers n ≥ 0.

This property of a sequence is closely related to a property of its generating

function.

Deﬁnition 7.63 A generating function f(x) of one variable is D-ﬁnite if

there exist polynomials q

(x), i =0,...,m with p

(x) =0such that



i=0

(x)u

(i)

=0,

where u

(i)

= d

u/dx

is the i-th derivative of u with respect to x.

Note that a sequence is P-recursive if and only if its generating function is

D-ﬁnite (see [183, Proposition 6.4.1]). Furthermore, every algebraic generat-

ing function (see Deﬁnition 2.40) is also D-ﬁnite (see [183, Proposition 6.4.6]),

so the sequence of coeﬃcients of an algebraic generating function is always

P-recursive. However, not every P-recursive sequence has an algebraic gener-

ating function. (For details, see [183, Chapter 6.4].) Thus the question is: Is

the generating function for {AW

[n]

(n)}

n≥0

algebraic? If not, is the sequence

at least P-recursive?

Theorem 7.64 Let τ be a permutation pattern of length three. Then the se-

quence f(n)=AW

[n]

(n) is P -recursive and satisﬁes the three term recurrence

p(n)f(n − 2) + q(n)f(n − 1) + r(n)f (n)=0,

where

p(n)=3(n − 3)(n − 1)(3n −5)(3n −4)(5n −4),

q(n) = 288 −1440n + 2780n

− 2435n

+ 976n

− 145n

, and

r(n)=2(n − 2)

n(n + 1)(5n −9).

282 Combinatorics of Compositions and Words

Proof The fact that f(n)isP -recursive follows easily from the expansion of

f(n) as a double sum using Theorem 7.61 and the theory developed in [129].

The polynomials p, q and r were found using the package MULTISUM (see

[172]) developed by Riese. 2

Corolla ry 7.65 The asymptotic behavior of f(n)=AW

[n]

(n) as n →∞for

τ ∈S

is given by

f(n) ≈ Cn

−2





for some constant C>0.

Proof This is a direct consequence of Theorem 7.64 and the theory of

asymptotics for P -recursive sequences (see [194]). 2

Since the exponents of n in the asymptotic expansion of a sequence with

an algebraic generating function are always nonnegative, Corollary 7.65 indi-

cates that the generating function of AW

[n]

(n) is transcendental (that is, not

algebraic).

7.3.4 Further results and generalizations

The results in the previous sections on avoidance of a pattern τ in words

can be generalized in two diﬀerent ways:

1. Avoidance of a set of patterns T in words.

2. Avoidance of a pattern or sets of patterns in compositions.

In both cases, the generalization is in the deﬁnition of the automaton. Once

we have deﬁned an appropriate automaton, we can then apply Theorem 7.34

to the respective adjacency matrix and replace τ by T and/or words by com-

positions. Note that the equivalence

∼ includes compositions, as each com-

position is also a word. Therefore, we only need to extend the equivalence for

the case of pattern avoidance of a set of patterns.

Deﬁnition 7.66 Given a set of patterns T , we deﬁne an equivalence relation

∼

on [k]

∗

(where [k]

∗

is the set of all ﬁnite words with letters from [k]) as

v ∼

w if for all words r ∈ [k]

∗

we have

vr avoids T ⇔ wr avoids T,

where a word u avoids T if u avoids all patterns in T simultaneously.

Note that Lemma 7.27 generalizes to the equivalence relation ∼

Automata and Generating Trees 283

Deﬁnition 7.67 The automaton A(T,k) for avoidance of a set of patterns

T in words is deﬁned by replacing E(τ,k) with E(T,k),thesetofequivalence

classes of ∼

ε

1

2

12

13

14

23

24

231

241

3, 4

1, 2

1, 3

1, 4

2, 3

2, 4

23 2

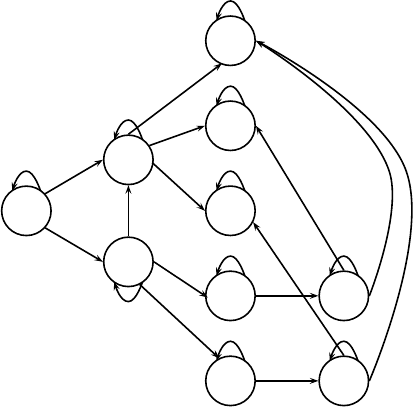
FIGURE 7.14: Automaton A({123, 132}, 4).

Example 7.68 Figure 7.14 shows the automaton for 4-ary words that avoid

the pair of patterns {123, 132}. Note that for this automaton, there are edges

from states that have labels with three letters to states that have two letter

labels; nevertheless, there is no cycle in this graph. (We have seen a similar

situation for the automaton of Example 7.32.) Using the order of states ε,

1, 2, 12, 13, 14, 23, 24, 213,and241, the adjacency matrix

for this automaton is given by

A({123, 132}, 4) =

⎡

⎢

⎣

2110000000

0101110000

0110001100

0002000000

0000200000

0000020000

0000002010

0000000201

0001100010

0001010001

⎤

⎥

⎦

284 Combinatorics of Compositions and Words

Note that even though the matrix with this ordering of states is not a triangu-

lar matrix, there is an ordering that results in a triangular adjacency matrix

(which one?). Using the Maple command

f:=simplify(evalm((1-x*A)^(-1)&*[1,1,1,1,1,1,1,1,1,1])[1]);

with(genfunc): rgf_expand(f,x,n);

with this adjacency matrix A gives the generating function

{123,132}

[4]

(x)=

− 2x +1

(1 − 2x)

and AW

{123,132}

[4]

(n)=(n

+ n +2)2

n−1

.ThecorrespondingMathematica

commands are

g[x_]:=Apply[Plus,Inverse[IdentityMatrix[10]-x A][[1]]]//Factor

SeriesCoefficient[g[x], {x,0,n}]

Now we will turn our attention to compositions.

Deﬁnition 7.69 For pattern avoidance in compositions, we deﬁne the au-

tomaton A(T,A) for any (ﬁnite) ordered subset A of N with E(T,A) as the

set of equivalence classes of ∼

, and label the edges between the state σ and

σa

 by x

instead of by a

. In this case, the edge labels are weights, unlike in

Deﬁnition 7.29, where the labels a

were for identiﬁcation only. The (i, j) en-

try of the associated weighted adjacency matrix now counts the total weight of

the edges between states i and j. An edge with multiple labels x

,...,x

has weight



j=1

Note that the use of weights on the edges in the case of compositions leads

to results in terms of generating functions rather than results on the number

of compositions of n that avoid a pattern τ or set of patterns T . We will now

present some results and examples on subsequence patterns, subword patterns

and generalized patterns in compositions.

Example 7.70 As indicated in Deﬁnition 7.69, we need to put weights on

the edges when enumerating compositions. It is easy to draw the automaton

for avoidance of the subsequence pattern τ = 123 in compositions with parts

in A =[3](do it ) to obtain the associated adjacency matrix as

A =

⎡

⎣

+ x

x 0

0 x + x

00x + x

⎤

⎦

Using the Maple command

factor(evalm( (1-A)^(-1)&*[1,1,1] )[1]);

or the Mathematica command