Heubach S., Mansour T. Combinatorics of Compositions and Words

Подождите немного. Документ загружается.

Automata and Generating Trees 295

If such an operator ϑ exists and it can be translated into a set of succession

rules of the form

Root:(b)

Rules:(d)  (c

)(c

) ···(c

q(d)

where b, d, c

≥ 0, and q : N → N, then the recursion can be described via

a generating tree. Elements of O

occur at the same level of the tree, and

any element of O

has as its children the elements of O

n+1

created by the

operator ϑ.

We illustrate the ECO method by enumerating several classes of words

avoiding pairs of generalized patterns. The main idea in Bernini at al. [23] is

to enumerate a special type of words avoiding a set of patterns via the ECO

method, and then to obtain the total number of words avoiding the set of

patterns from the count of the special words. We need some notation before

describing the process.

Deﬁnition 7.90 We call a word reduced if it is in reduced form (see Deﬁni-

tion 1.20), and denote the set of reduced k-ary words of length n that avoid a

set of patterns T by



[k]

(T ). The number of such words will be denoted by



[k]

(n).

Note that each w ∈



[m]

(T ) is associated with exactly





distinct words

in AW

[k]

(T ) as we can replace the set of letters of w with any possible subset

of [k]havingm elements, taking care of preserving the relative order of the

letters. For instance, the reduced word 121321 ∈



[3]

({1–22, 2–12})is

associated with the following





= 10 words of AW

[5]

({1–22, 2–12}):

121321 121421 121521 131431 131531

141541 232432 232532 242542 343543

Thus

[k]

(n)=



m=0







[m]

(n), (7.7)

and we can restrict ourselves to ﬁnding an operator ϑ for the sets



[m]

(T ).

The ECO method now consists of the following steps:

1. Find a recursion for



[k]

(T ), that is, identify the operator ϑ.

2. If possible, translate ϑ into a generating tree.

3. If possible, determine the generating function for



[k]

(n), or even

better, derive a closed formula.

Then apply (7.7) to obtain the corresponding results for AW

[k]

(n), assuming

Steps 2 and 3 of the ECO method were successful.

296 Combinatorics of Compositions and Words

So how can we create reduced words of length n + 1 from those of n?

Usually, when recursively constructing words we append a letter to the right

end of the word. We do the same thing here, except we have to ensure that

the resulting word is again a reduced word and that none of the patterns

in T are created. To assist with this task, we visualize the word as a path,

where the height of the path corresponds to the letter. Since we are dealing

with words (as opposed to permutations) we can append letters that have

previously occurred (indicated by lines) or new letters (indicated by circles).

To account for new letters we identify the regions above, between, and below

the lines. These regions and the lines encode the potential insertion letters

and we will call them active sites.

Now we identify for a word w ∈



[m]

(n)theallowed active sites,those

that do not create any of the patterns in T . We mark regions and lines that

are allowed by an empty circle. Obviously, this depends very much both

on the word w and the patterns T to be avoided, which seems to make it

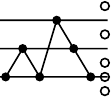
hard to ﬁnd a general recursion. For example, Figure 7.22 shows the word

121321 ∈



[3]

({1–22, 2–12}) with the allowed active sites identiﬁed. Since

121321 ends in a 1, avoidance of 1–22 does not put any restrictions on the

active sites. However, avoidance of 2–12 eliminates all previously occurring

values bigger than the last one, that is, we cannot append the letters 2 or 3.

FIGURE 7.22: Allowed active sites for 121321 ∈



[3]

({1–22, 2–12}).

Once we have identiﬁed the allowed active sites, we have to describe what

happens as the respective letter is appended. Appending a letter that has

previously occurred to w ∈



[m]

(T ) creates a word w



∈



[m]

n+1

(T ). If

we insert a new value, that is, we choose an allowed active region, then we

have to make some adjustments to the letters in w. If the region between

i and i + 1 is chosen (for i =0,...,m), then the letter appended is i +1,

and all letters j ≥ i +1 in w get mapped to j + 1. This creates a word



∈



[m+1]

n+1

(T ). Obviously, this case is only possible if m<k.Notethat

the process of creating words of length n + 1 satisﬁes the conditions for an

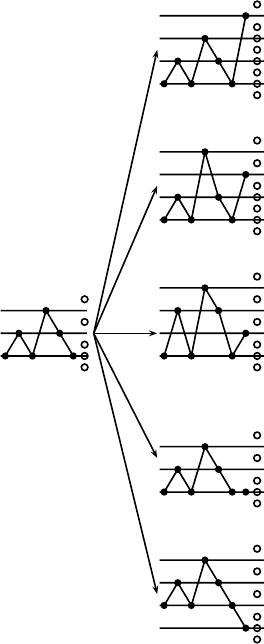
operator ϑ stated in Theorem 7.89. Figure 7.23 shows the ﬁve words created

from 121321 ∈



[3]

({1–22, 2–12}) with their allowed active sites indicated.

The allowed values were added in order from top to bottom. For example,

insertion above the top line does not require relabeling of any letters in w.

Automata and Generating Trees 297

However, insertion in the region between 2 and 3 requires that any letter 3

in w is renamed to a 4, thus mapping 121321 to w = 1214213. The only

insertion on a line is the fourth case, which results in a reduced word on

[3]. All together, starting from the word 121321 ∈



[3]

({1–22, 2–12}), we

can construct ﬁve new reduced words of length 7, namely 1213214, 1214213,

1314312, 1213211, and 2324321.

FIGURE 7.23: Generating the reduced words of length 7 from 121321.

After having explored a particular example, we need to ﬁnd the general

structure of the insertions for words w ∈



[m]

(T ) avoiding the pair of pat-

terns T = {1–12, 2–21}. Suppose that the last letter of w is h ≤ m.Sincethe

patterns to be avoided have repeated letters, we distinguish two cases:

298 Combinatorics of Compositions and Words

• h occurs for the ﬁrst time in w.

• h has previously occurred in w.

To distinguish these two cases, we use the following notation: the label (m

)

denotes a word of



[m]

(T ) ending with (the ﬁrst occurrence of) the letter

h;thelabel(¯m

) denotes a word in



[m]

(T ) ending with the letter h,where

h also appears in some previous position. Now let’s see what happens in each

case. In the ﬁrst case, h cannot be part of an occurrence of either 1–12 or

2–21, and we can add any letter on the right-hand side. Since w is a reduced

word on [m], the letters 1,...,mhave occurred before, and so insertion of any

of these letters results in the labels ( ¯m

) ···(¯m

). Insertion of any new letter

i will create a word on the alphabet [m + 1] for which the letter i is the ﬁrst

occurrence, resulting in the labels

((m +1)

) ···((m +1)

m+1

In the second case, h can play the role of 1 in the pattern 1–12 and therefore

we cannot add any value that is bigger than h. For the pattern 2–21, the

opposite is true, that is, we cannot add any value that is smaller than h,soh

is the only allowed value. Thus, only one word gets created and the succession

rule is given by

(¯m

)  (¯m

The smallest word is the word 1, which for obvious reasons avoids simultane-

ously 1–12 and 2–21, and therefore, the root is given by (1

). All together we

have the following succession rules:

Root:(1

)

Rules:(m

)  (¯m

) ···(¯m

)((m+1)

) ···((m+1)

m+1

)form<k

(¯m

)  (¯m

These succession rules do not easily allow for enumeration, so let’s look

at them more closely. First of all, in the rule ( ¯m

)  (¯m

), the value of h

does not matter at all. What is important is the parameter m as it plays

a signiﬁcant role in the enumeration. Since each vertex with this label has

exactly one child, we use the label (1

) instead, and rewrite the rule as

)  (1

), where (1

) denotes a reduced word on the alphabet [m]whose

last letter appears somewhere else in the word. Now let’s look at the rule

for the ﬁrst case. Here again, the value of h is unimportant. The vertex

with label (m

)hasm +(m +1) = 2m + 1 children, so we should use the

label (2m + 1) instead for a reduced word on the alphabet [m] whose last

letter does not appear anywhere else in the word. The rule thus translates to

(2m +1) (1

)

(2m +3)

m+1

. Making the empty word the root with label

(1) puts the words of length n at level n in the generating tree and we obtain

this modiﬁed set of succession rules:

Automata and Generating Trees 299

Root:(1)

Rules:(2m +1) (1

)

(2m +3)

m+1

for m<k

)  (1

So what can we say about the new set of succession rules? From their

deﬁnition, it is clear that

(i) each label (2m +1) and(1

) represents a word on the alphabet [m];

(ii) the unique labels appearing at level n of the generating tree are (1

), ···,(1

n−1

)and(2n +1).

Therefore



[m]

(n) is either the number of labels (1

) at level n if m<n,

or the number of labels (2m +1)atleveln if m = n. This results in the

following explicit formula for



[m]

(n) given by Bernini et al.

Theorem 7.91 [23, Theorem 4.1] For ﬁxed n and k and m ≤ k, we have



[m]

(n)=



m · m! for m<n

n! for m = n

Proof Let a

n,m



[m]

(n) be the number of reduced words of length

n on the alphabet [m]. From the succession rules we obtain the following

recursions:

n,n

= n · a

n−1,n−1

(7.8)

n,n−1

=(n − 1) ·a

n−1,n−1

(7.9)

n,k

= a

k+1,k

(7.10)

where the last equation holds for k<n− 1. Since a

1,1

= 1, we immediately

obtain from (7.8) that a

n,n

= n!. This result together with (7.9) gives that

n,n−1

=(n − 1)(n − 1)!. Finally, (7.10) yields a

n,k

= k · k!, for k<n− 1.

Obviously, these formulas hold only for m ≤ k, and therefore we can use only

a ﬁnite part of the generating tree. 2

As an easy consequence of Theorem 7.91 we obtain the following proposi-

tion.

Proposition 7.92 [23, Theorem 4.2] The number of k-ary words of length n

that avoid the pair of generalized patterns T = {1–12, 2–21} is given by

[k]

(n)=





n−1

m=0

m · (k)

+(k)

for n ≤ k



k−1

m=0

m · (k)

for n>k

where (k)

= k(k − 1) ···(k − m +1)=k!/m!.

300 Combinatorics of Compositions and Words

Proof The proof follows from Theorem 7.91 and (7.7). 2

Bernini et al. [23] have used the ECO method for several pairs of gen-

eralized patterns of type (2, 1) and have obtained either an explicit formula

or a generating function. We summarize their results in Table 7.3 and also

indicate which cases are still missing for a complete classiﬁcation of the pairs

of generalized patterns of type (2, 1) with repeated letters. As before, the

complement and reversal maps reduce the total number of diﬀerent pairs to

be considered. Bernini et al. pose the pairs with ∗ as questions for further

research.

TABLE 7.3: Results for pairs of patterns of type (1, 2)

1–11, 1–12 [23, Thm 6.3]

1–11, 1–21

[23, Thm 7.1]

1–11, 1–22

[23, Thm 7.2]

1–12, 1–21

1–12, 1–22

1–12, 2–11

1–12, 2–12

1–12, 2–21

Theorem 7.92

1–21, 1–22

1–21, 2–11

1–21, 2–12

[23, Thm 5.1]

2–11, 1–22

[23, Thm 7.3]

Note that we can obtain simpliﬁed expressions for some of the generating

functions given in [23]. For instance, in Theorem 7.3 of [23] the generating

function AW

[k]

(x)forT = {2–11, 1–22} is given as

{2–11,1–22}

[k]

(x)=



m=0

(k)

·x

k−1



m−1

i=1

(1 − ix)

·(1 − x)

We will derive a simpler generating function for the Wilf-equivalent pair

T = {11–2, 22–1}∼{2–11, 1–22}

using generating function techniques.

Theorem 7.93 The generating function for k-ary words w of length n that

avoid {11–2, 22–1} is given by

[k]

(x)=

1+(k − 1)x

1 − kx +(k − 1)x

Automata and Generating Trees 301

Proof Deﬁne AW

[k]

···w

|x) to be the generating function for k-ary

words w of length n that avoid T and start with w

···w

. Clearly,

[k]

(x)=1+



i=1

[k]

(i|x), (7.11)

where

[k]

(i|x)=x +



j=i

[k]

(ij|x)+AW

[k]

(ii|x). (7.12)

Let w avoid T .Ifw

= w

= i, then avoiding 11–2 and 22–1 implies that we

have to have w

= i for all j, and therefore, AW

[k]

(ii|x)=

1−x

.Ifw

= w

then AW

[k]

(ij|x)=xAW

[k]

(j|x) because both patterns start with repeated

letters. All together, (7.12) can be written as

[k]

(i|x)=x + x



j=i

[k]

(j|x)+

1 − x

= x + x(AW

[k]

(x) − AW

[k]

(i|x) − 1) +

1 − x

where the second equality follows from (7.11). Thus,

(1 + x)AW

[k]

(i|x)=xAW

[k]

(x)+

1 − x

Summing over i =1, 2,...,k leads to

(1 + x)(AW

[k]

(x) − 1) = kxAW

[k]

(x)+

1 − x

which gives the desired result after appropriate simpliﬁcation. 2

We now obtain a formula for the generating function AW

{11–2,12–2}

[k]

(x), one

of the cases listed as open in [23] by using the scanning-element algorithm.

Theorem 7.94 Let T = {11–2, 12–2}, P (n, k)=AW

[k]

(T ),

P (n, k)={w ∈AW

[k]

(T ) | w

= w

for j =2,...,n},

and let P

(x; v) and P

(x; v) be deﬁned as in (6.23).Then

(x; v)=1+x +

1 − v

(x; v) − v

k−1

(x;1))

1 − v

(

(x;1)− P

(x; v)) + x



i=1

i−1

(x;1),

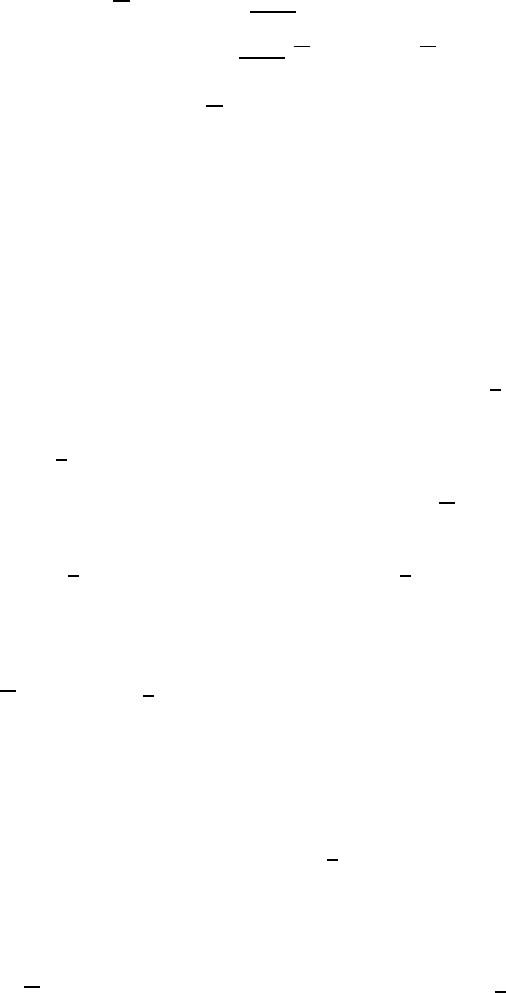
302 Combinatorics of Compositions and Words

and

(x; v)=x +

1 − v

k−1

(x; v) − v

k−1

(x;1))

1 − v

(

k−1

(x;1)− vP

k−1

(x; v)),

where P

(x; v)=1and P

(x; v)=0.

Proof We use the scanning-element algorithm to ﬁnd a formula for the

generating function for the number of k-ary words of length n that avoid both

11–2 and 12–2. From the deﬁnition of the algorithm (see Section 6.5.3) we

have that p(n, k)=



i=1

p(n, k; i)and

p(n, k; i)=

i−1



j=1

p(n, k; i, j)+p(n, k; i, i)+



j=i+1

p(n, k; i, j)

i−1



j=1

p(n − 1,k; j)+p(n −2,i)+



j=i+1

p(n − 1,k; j), (7.13)

where

p(n, k; j)isthenumberofk-ary words of length n that avoid both 11–2

and 12–2 such that the letter j occurs only at the beginning of the word.

Applying the scanning-element algorithm now for

P (n, k)weobtain

p(n, k; i)=

i−1



j=1

p(n − 1,k− 1; j)+

k−1



j=i

p(n − 1,k− 1; j), (7.14)

as the letter i cannot occur anywhere else in the word, and we therefore can

map the alphabet [k] \{i} to [k − 1]. Let P

n,k

(v)=



i=1

p(n, k; i)v

i−1

and

n,k

(v)=



i=1

p(n, k; i)v

i−1

. Multiplying the recurrence relations (7.13) and

(7.14) by v

i−1

and summing over i =1, 2,...,k,wegetthatforalln ≥ 2

n,k

(v)=



i=1

i−1



j=1

p(n − 1,k; j)+



i=1

i−1

p(n − 2,i)



i=1

i−1



j=i+1

p(n − 1,k; j),

and

n,k

(v)=



i=1

i−1



j=1

p(n − 1,k− 1; j)+



i=1

i−1

k−1



j=i

p(n − 1,k− 1; j).

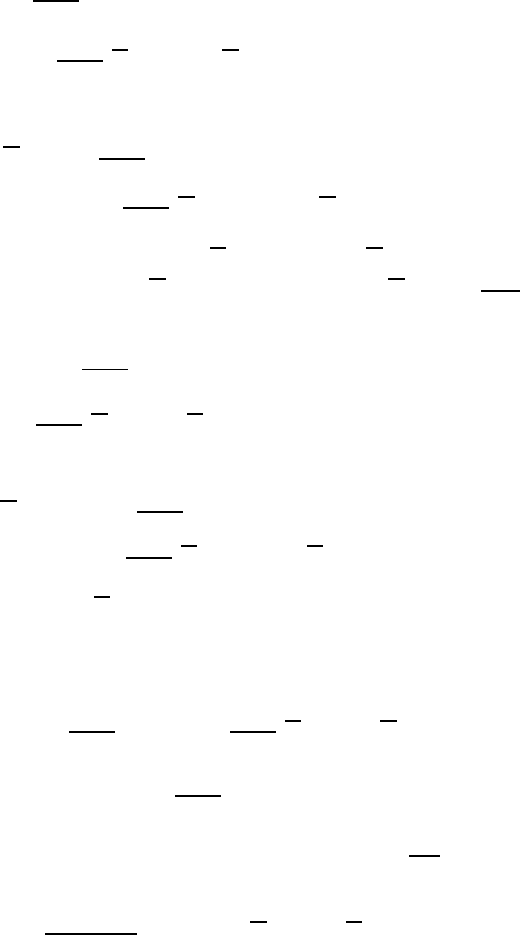
Automata and Generating Trees 303

Change of order of summation leads to

n,k

(v)=

1 − v

n−1,k

(v) − v

k−1

n−1,k

(1))

1 − v

(

n−1,k

(1) − P

n−1,k

(v)) +



i=1

i−1

p(n − 2,i),

and

n,k

(v)=

1 − v

n−1,k−1

(v) − v

k−1

n−1,k−1

(1))

1 − v

(

n−1,k−1

(1) − vP

n−1,k−1

(v)).

Let P

(x; v)=



n≥0

n,k

(v)x

and P

(x; v)=



n≥0

n,k

(v)x

.Usingthe

initial conditions P

0,k

(v)=1,P

0,k

(v) = 0, and P

1,k

(v)=P

1,k

(v)=

1−v

,we

obtain that

(x; v)=1+x +

1 − v

(x; v) − v

k−1

(x;1))+x



i=1

i−1

(x;1)

1 − v

(

(x;1)− P

(x; v)) (7.15)

and

(x; v)=x +

1 − v

k−1

(x; v) − v

k−1

(x;1))

1 − v

(

k−1

(x;1)− vP

k−1

(x; v)), (7.16)

where P

(x; v)=1andP

(x; v)=0. 2

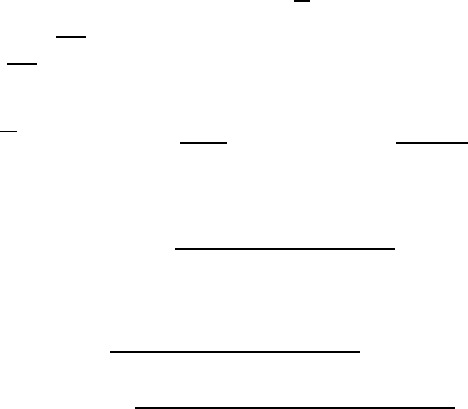
The results of Theorem 7.94 allow us to iteratively compute AW

[k]

(x)=

(x; 1). Rewriting (7.15) so that we can apply the kernel method leads to

(x; v)



1 −

1 − v



=1+x +

1 − v

(

(x;1)− P

(x; v))



k−1

−

1 − v



(x;1)+x

k−1



i=1

i−1

(x;1). (7.17)

Setting the factor of P

(x; v) to zero in (7.17) results in v =

1+x

for all values

of k. Substituting this value of v into (7.17) and solving for P

(x;1) leads to

(x;1) =

(1 + x)

k−1

1 − x

(1 + x)(1 +

(x;1)− P

(x;1/(1 + x)))

+ x

k−1



i=1

i−1

(x;1)

. (7.18)

304 Combinatorics of Compositions and Words

We now compute AW

[k]

= P

(x;1)fortheﬁrstfewvaluesofk.Fork =1,

we obtain from the initial conditions that

(x; v)=x, and from (7.18)

that P

(x;1) =

1−x

. Substituting these functions into (7.17) yields that

(x; v)=

1−x

. We follow the same procedure for k =2, 3, and 4, using

(7.16) instead of the initial conditions to obtain that

(x; v)=x + x

1 − x

and P

(x;1) =

1+x

(1 − x)

Similarly, we can ﬁnd that

(x;1) =

1+3x

+2x

+3x

− x

(1 − x)

and

(x;1) =

1+6x

+8x

+21x

+24x

(1 − x)

20x

+ x

− 14x

− 6x

+2x

+ x

(1 − x)

Note that the scanning-element algorithm can also be applied to some of

the other pairs of letters which are listed as open problems in Table 7.3.

We now return to the ECO method and its applications. So far we have

seen the ECO method applied to pattern avoidance in words. A somewhat

diﬀerent focus was used by Baril and Do [17]. They used the ECO method

to encode the generating trees for various types of restricted compositions

via restricted permutations. For example, they consider (1,k)-compositions,

compositions without the part k, and compositions whose largest part is p.

The focus of their paper is generating these compositions via permutations

for which eﬃcient (that is, constant time) recursive algorithms are known. So

the succession rules and the encodings are given without much detail. Since

our focus is not on algorithmic creation but rather on the structure of the

compositions, we will give an interpretation of the succession rules in terms

of the recursive creation of the respective compositions. We start by deriving,

the succession rules for (1,k)-compositions (see Example 3.14), which were

studied by [7, 17, 51].

Theorem 7.95 (compare to [17, Table 1]) The system of succession rules for

the (1,k)-compositions is given by

Root:(1

)

Rules:(1

)  (1

i+1

), for 0 ≤ i<k− 2

k−2

)  (2)

(2)  (2)(1

)