Heubach S., Mansour T. Combinatorics of Compositions and Words
Подождите немного. Документ загружается.


Automata and Generating Trees 265
Proof The corollary follows from the proof of Theorem 7.37, since the
longest simple path is of length M,andN(P, n)=(d − 1)
n−j
n
j
forapath
of length j.Ifτ is a pattern of length + 1, then all the words of length j ≤
avoid τ, and therefore, AW
τ
[k]
(j)=
j
i=0
a
i
(d − 1)
j−i
j
i
= k
j
. Comparing
coefficients in the binomial expansions, we have that a
i
=(k − d +1)
i
for
i =0, 1,...,. 2
Thus we can obtain exact results very nicely for any pattern or family of
patterns for which the assumptions of Corollary 7.38 apply. The increasing
patterns to be discussed in Section 7.3.3 are one such family. Finding other
patterns or families of patterns remains an open question (see Research Di-
rection 7.2). On the other hand, specifying the alphabet as opposed to the
pattern gives a very nice exact result.
Example 7.39 If τ is any pattern of length +1 with exactly d different
letters and [k]=[d], then Corollary 7.38 gives that
AW
τ
[d]
(n)=
j=0
(d − 1)
n−j
n
j
.
We can also obtain explicit results using the program TOU
FORMULA,
which utilizes Theorem 7.34 for computing an explicit formula for AW
τ
[k]
(n).
This Maple program is posted on Toufik Mansour’s homepage [139] and also
listed in Appendix G.5. It uses as input the adjacency matrix of the au-
tomaton A(τ,k) from the C++ program TOU
AUTO and returns the exact
formula for AW
τ
[k]
(n). These two programs allow us to get an explicit for-
mula for AW
τ
[k]
(n) for any given τ and k ≥ 1, limited only by computing
power. Using [b
0
,b
1
,...,b
d
]
x
=
d
j=0
b
j
n
j
x
n−j
as a shorthand notation, Ta-
ble 7.2 presents the explicit formulas for AW
τ
[k]
(n) for all patterns τ ∈S
4
for
k =3,...,6. The complete analysis for all the subsequence patterns of length
four is posted on Toufik Mansour’s homepage [140].
We now turn to a family of patterns, namely the increasing patterns of
length +1.
7.3.3 The increasing patterns
In [169], Regev gave a complete answer for the asymptotic behavior of
AW
τ
[k]
(n)asn →∞for the increasing pattern τ
=12···( +1). Hisproof
made use of results from representation theory. We will present a different
proof of Regev’s result based on both the structure of the automaton for
increasing patterns and on results on Young tableaux given by Br¨and´en and
Mansour [27].
We start by deriving the structural results for the automaton A(τ
,k)which
allow us to apply Corollary 7.38 to obtain an exact result for the constant in
the asymptotic expression.
© 2010 by Taylor and Francis Group, LLC
266 Combinatorics of Compositions and Words
TABLE 7.2: Avoidance of permutation patterns τ ∈S
4
in words
τ k AW
τ
[k]
(n)
1234, 1243 3 [1]
3
1432, 2143 4 [1, 1, 1, 1]
3
5 [1, 2, 4, 8, 11, 10, 5]
3
6 [1, 3, 9, 27, 66, 126, 183, 189, 126, 42]
3
1324 3 [1]
3
4 [1, 1, 1, 1]
3
5 [1, 2, 4, 8, 11, 10, 5, 1]
3
6 [1, 3, 9, 27, 66, 126, 183, 197, 152, 80, 26, 4]
3
1342 3 [1]
3
4 [1, 1, 1, 1]
3
5 [1, 2, 4, 8, 11, 10, 4]
3
6 [1, 3, 9, 27, 66, 126, 176, 168, 96, 24]
3
1423 3 [1]
3
4 [1, 1, 1, 1]
3
5 [1]
2
+[0, 3, 3, 9, 10, 11, 3]
3
6 [13, 1]
2
+[−12, 15, −2, 37, 57, 134, 169, 167, 76, 12]
3
2413 3 [1]
3
4 [1, 1, 1, 1]
3
5 [10, 4, 1]
2
+[−9, 8, 1, 9, 11, 10, 2]
3
6 [96, 28, 5]
2
+[−95, 71, −36, 54, 52, 132, 167, 137, 44, 4]
3
Lemma 7.40 Let k ≥ be given and let τ
=12···( +1). For any set
S = {s
1
< ···<s
m
}⊆[k] and j ∈ [k],let
S
j
= {s
1
< ···<s
i−1
<j<s
i+1
< ···<s
m
},
where i is the index such that s
i−1
<j≤ s
i
(s
0
:= 0,s
m+1
:= k +1).In
addition, let w
S
be the word consisting of the elements of S listed in increasing
order, where ε = w
∅
. Then the transition function Δ for the automaton
A(τ
,k) is given by
Δ(w
S
,j)=
⎧
⎪
⎨
⎪
⎩
w
S
j
if |S
j
|≤, and j<k− +1+m
w
S
if j ≥ k − +1+m
τ
otherwise
.
and the number of states is
|E(τ
,k)| =
k
+1.
In particular, the loops of w
S
are the elements of S∪{k, k−1,...,k−+m+1},
and therefore, w
S
has exactly loops.
To follow the proof of this result it may be helpful to look at Figure 7.7
which shows the automaton A(τ
2
,k).
© 2010 by Taylor and Francis Group, LLC
Automata and Generating Trees 267
Proof It is clear that the words w
S
are representatives of different classes.
Since we are to avoid an increasing pattern of length +1, we have only
k −( +1)+1 = k − letters available in the alphabet from which to start the
full pattern. At each step, one more letter is available as the partial pattern
still to be avoided shrinks by one letter. In addition, there is the state τ.
Thus,
|E(τ
,k)| =1+
i=0
k − ( +1)+i
i
=1+
k
,
where we have used (A.6) with a = k − − 1.
Let v ∈AW
[k]
∗
(τ
). We say that an increasing subword x
1
x
2
···x
j
of v is
extendible if x
j
≤ k + j − − 1, that is, x
1
x
2
···x
j
can be extended into an
occurrence of τ
using letters from [k]. Suppose that the longest extendible
increasing subsequence in v consists of s ≤ letters. For 1 ≤ j ≤ s let
r
j
(v):=min{x
j
| x
1
x
2
···x
j
is an extendible subword of v}.
Clearly r
1
(v) <r
2
(v) < ···<r
s
(v). Let
S = {r
1
(v),r
2
(v),...,r
s
(v)}.
Then we see that w
S
A
∼ v, that is, we have determined the equivalence class
for any v. The statement about the transition function Δ follows from the
construction of the sets S
j
together with arguments analogous to those given
in Example 7.30 for the automaton of the pattern τ
2
= 123. The transition
function immediately gives that the elements of S are loops for w
S
. In addi-
tion, for j ∈{k, k−1,...,k−+ m+1}, w
S
j is not extendible and therefore
w
S
j = w
S
. 2
In order to give the promised alternative proof of Regev’s result we will
need some standard notions and notation from the theory of partitions and
symmetric functions. We will state the necessary definitions and refer the
reader to an in-depth discussion of these topics in [183, Chapter 7].
Definition 7.41 To each partition (see Definition 1.1) we can associate a
Young diagram as follows: for a partition
λ =(λ
1
,λ
2
,...,λ
k
) ∈ N
k
with
k
i=1
= n and λ
1
≥ λ
2
≥ ··· ≥ λ
k
, the Young diagram is an array of k
left-justified boxes with λ
i
boxes in the i-th row, where rows are labeled from
top to bottom. The vector
λ is referred to as the shape of the Young diagram.
If we have a partition into k equal parts of size m, that is,
λ =(m,m,...,m),
then we write λ
k,m
and refer to the diagram as having size k × m.AYoung
tableau (plural tableaux) is a filling of a Young diagram with letters from some
alphabet. If the entries in the Young tableau are all distinct and entries in all
rows and columns are strictly increasing, then the filling is called a standard
Young tableau. If the entries increase weakly in rows and increase strictly
© 2010 by Taylor and Francis Group, LLC
268 Combinatorics of Compositions and Words
in columns, then the Young tableau is called a semi-standard tableau.The
weight of a Young tableau is given by the sequence of values that record the
number of times each integer appears in the Young tableau (similar to the
definition of the content vector).
Note that it is customary to refer to partitions as vectors
λ in the context
of Young tableaux, and to write them as a vector, while in other contexts,
partitions are written as sequences.
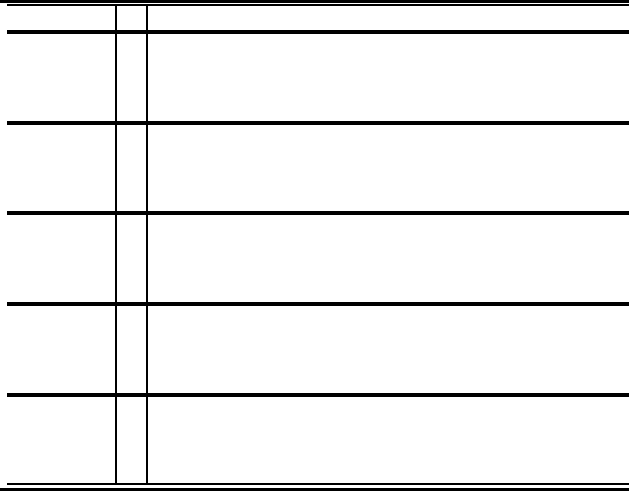
Example 7.42 Figure 7.9 shows the five semi-standard Young tableaux of
shape (2, 2). The leftmost two tableaux are standard Young tableaux. The
weights for the five tableaux are: (1, 1, 1, 1), (1, 1, 1, 1), (1, 1, 2), (2, 2),and
(2, 1, 1). Clearly, standard Young tableaux always have weight vectors consist-
ing of all ones.
4
3
2
1
4
2
3
1
3
2
3
1
2
1
2
1
3
1
2
1
FIGURE 7.9: Young tableaux of shape λ
2,2
(or size 2 × 2).
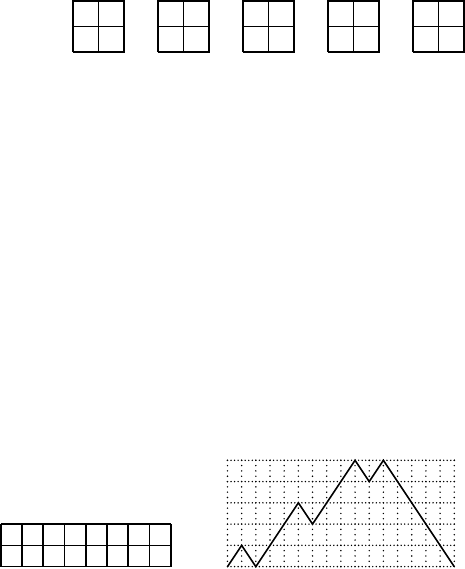
Example 7.43 Standard Young tableaux of size 2 ×n are enumerated by the
Catalan numbers, which also enumerate Dyck paths (see Example 2.50).This
can be seen using the following bijection: given a standard Young tableau of
size 2 × n, read the integers from 1 to 2n in order, and create a path in the
integer lattice starting at (0, 0) by placing an up-step if the integer occurs in
the top row, and a down-step if the integer occurs in the bottom row. It is not
hard to show that this mapping is a bijection (see[183,Exercise6.19(ww)] ).
Figure 7.10 shows a 2 × 8 standard Young tableau and its associated Dyck
path.
134578911
2 6 10 12 13 14 15 16
FIGURE 7.10: Standard Young tableau and associated Dyck path.
© 2010 by Taylor and Francis Group, LLC
Automata and Generating Trees 269
Young diagrams may remind you of Ferrers diagrams (see Definition 6.13),
and indeed, they refer to the same type of combinatorial object. In drawing
the Ferrers diagrams, we have followed the French convention (rows numbered
from bottom to top, like the Cartesian coordinate system). By contrast, we
will draw the Young diagrams and corresponding Young tableaux following the
English convention (rows numbered from top to bottom, like matrix indices),
thereby accommodating all tastes. Apparently, this nomenclature of English
and French conventions started out as a joke. In his book on symmetric
functions [135, p.2], MacDonald suggests to readers preferring the French
convention to “read [his] book upside down in a mirror.” (The French also
prefer to have the column index listed before the row index – a convention
we do NOT follow). The real difference between Ferrers diagrams and Young
diagrams is in their content – fillings of Ferrers diagrams consist of zeros and
ones, whereas Young tableaux are filled with positive integers.
Definition 7.44 A partially ordered set or poset is a set P together with a
binary order relation ≤ satisfying the following three properties:
1. For all x ∈ P , x ≤ x (reflexivity).
2. If x ≤ y and y ≤ x,thenx = y (antisymmetry).
3. If x ≤ y and y ≤ z,thenx ≤ z (transitivity).
We use x ≥ y to mean y ≤ x, x<yto mean that x ≤ y and x = y,and
x>yto mean y<x. Two elements x and y of P are comparable if x ≤ y
or y ≤ x;o
therwise,x and y are incomparable.Thedual P
of a poset P is
defined on the elements of P with order x ≤ y in P
⇔ y ≤ x in P .IfP and
P
are isomorphic, then P is called self-dual.
Example 7.45 The following sets with their respective orders are familiar
posets.
(1) Any collection of sets together with set-inclusion, that is, S ≤ T if S ⊆
T .
(2) X
k
together with the component-wise order induced by the order of X:
for x, y ∈ X
k
, x ≤
X
k y if and only if x
i
≤
X
y
i
for i =1, 2,...,k.
(3) The set of Young diagrams together with the component-wise order. Vi-
sually, a Young diagram
λ ≤ μ if and only if the Young diagram for
λ
fits inside the Young diagram of μ. The poset of Young diagrams defined
by {μ|μ ≤
λ} is denoted by λ
λ
1
,λ
2
,···,λ
k
.
Definition 7.46 An (induced) subposet of P is a subset Q of P together
with a partial ordering of Q such that for x, y ∈ Q we have
x ≤ y in Q ⇔ x ≤ y in P.
© 2010 by Taylor and Francis Group, LLC
270 Combinatorics of Compositions and Words
The order on Q is called the induced order. In particular, the (closed ) interval
[x, y]={z ∈ P |x ≤ z ≤ y} is defined whenever x ≤ y.
Definition 7.47 A chain (or totally ordered set or linearly ordered set) is a
poset in which any two elements are comparable. A subset C of a poset P is
called a chain if C is a chain when regarded as a subposet of P .Thelength
of a finite chain C is defined as (C)=|C|−1.Amaximal chain is a chain
of maximal length in P . An order-preserving bijection from P to the poset
[n] is called a linear extension of P. The number of linear extensions of P is
denoted by e(P ).Anorder ideal of P is a subset I of P such that if x ∈ I
and y ≤ x,theny ∈ I. The set of all order ideals of P ,
ordered by inclusion,
forms a poset denoted by J(P ).
It can be shown (see [182, Section 3.5]) that e(P ) is equal to the number of
maximal chains in J(P ).
Definition 7.48 An (order) lattice is a poset P in which every pair of ele-
ments has both a unique supremum (or least upper bound) and an infimum
(or least lower bound).Abounded lattice has a least element
ˆ
0 and a largest
element
ˆ
1,where
ˆ
0 ≤ x ≤
ˆ
1 for all x ∈ P .
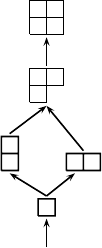
Example 7.49 (Young lattice) We will look at the poset P =[∅,λ
2,2
],the
set of Young diagrams whose shape is contained in (2, 2). The order of the
shapes is by component-wise comparison. This poset is a lattice, as can be
clearly seen from Figure 7.11, and is referred to as the Young lattice.For
example, the infimum of (2, 1) and (1) is (1),andtheirsupremumis(2, 1).
The largest element is
ˆ
1=(2, 2) and the least element is
ˆ
0=∅.Thetwo
maximal chains are {∅, (1), (2), (2, 1), (2, 2)} and {∅, (1), (1, 1), (2, 1), (2, 2)}
of length four. The set I = {∅, (1), (1, 1)} constitutes one of the six order
ideals of P. Note that by definition of the maximal chain, its elements consist
of shapes that differ exactly by one box. Therefore, the maximal chain has
length 2 · 2=4, and in general, the maximal chain in [∅,λ
k,m
] has length
k · m.
Definition 7.50 Two posets P and Q are isomorphic if there exists an order-
preserving bijection Φ:P → Q whose inverse is order-preserving, that is
x ≤ y in P ⇔ Φ(x) ≤ Φ(y) in Q.
We can now define a partial order on A(τ
,k) that is isomorphic to a well-
known poset.
Theorem 7.51 Let the partial order on the states in A(τ
,k) be defined as
follows:
x≤y⇔ there exists a path from x to y in A(τ
,k).
© 2010 by Taylor and Francis Group, LLC
Automata and Generating Trees 271
∅
FIGURE 7.11: Young lattice [∅,λ
2,2
].
Then this partial order is isomorphic to J([] ×[k −]), the order ideal of the
poset [] ×[k − ](with the component-wise order).
Proof Let S, T ⊆ [k]. Without loss of generality, we can assume that
S = {s
1
<s
2
< ···<s
} and T = {t
1
<t
2
< ···<t
}.
(If |S| <, then we can extend the set by appending the values {k + s −
1 − , k + s +2− ,...,k},wheres = |S|, and likewise for T .) We claim the
following:
There exists a path from w
S
to w
T
⇔s
i
≥ t
i
for all 1 ≤ i ≤ . (∗)
If there is an edge (that is, path of length one) from w
S
to w
T
then by
Lemma 7.40 we are done. For paths of length j ≥ 2, the claim follows by
induction on the length of the path. To prove the other direction, assume
that s
i
≥ t
i
for all 1 ≤ i ≤ . Consider the path
w
S
t
1
−→ w
S
t
1
t
2
−→ w
S
t
1
t
2
t
3
−→···
t
−→ w
S
t
1
t
2
···t
.
It is not hard to see that w
S
t
1
t
2
···t
= w
T
, as the path successively
transforms S into T by definition of Δ, and therefore (*) holds. We now
establish a bijection between the partial order on the automaton and the
Young lattice [∅,λ
,k−
]. Let s =(s
1
,s
2
,...,s
) consist of the elements of S
ordered by size, and define
Φ(s)=(s
− , s
−1
− +1,...,s
1
− 1).
Because the s
i
are strictly increasing and i ≤ s
i
≤ k, the function Φ produces
a Young diagram contained in × (k − ). Likewise, we can obtain a vector
© 2010 by Taylor and Francis Group, LLC
272 Combinatorics of Compositions and Words
s with distinct elements ordered by size when starting from a Young diagram
λ. Using the bijection
Ψ((λ
1
,λ
2
,...,λ
)) = (k − − λ
,...,k− − λ
1
),
we see that [∅,λ
,k−
] is its own dual. Therefore,
w
S
≤w
T
⇔Ψ(Φ(s)) ≤ Ψ(Φ(
t)),
that is, the partial order on the automaton is order-isomorphic to the Young
lattice [∅,λ
,k−
]. Now the statement follows from the simple fact that
[∅,λ
,k−
] is isomorphic to J([] × [k −]). 2
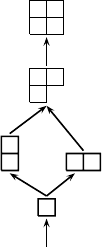
Example 7.52 Using the bijections given in the proof of Theorem 7.51, we
can give the order lattice for the automaton A(123, 4). We illustrate how to
associate states and Young shapes for the state 13, which has set S = {1, 3}
and vector s =(1, 3).Since =2and k =4, Φ((1, 3)) = (3−2, 1−1) = (1, 0).
The dual is obtained by Ψ((1, 0)) = (2 −0, 2 −1) = (2, 1). Thus the state 13
is associated with the Young shape (2, 1). Figure 7.12 shows the Young lattice
[∅,λ
2,2
] together with the associated states of the automaton A(123, 4).
∅
ε
2
1
23
13
12
FIGURE 7.12: Young lattice [∅,λ
2,2
] with associated states of A(123, 4).
So far we have established a correspondence between the states of the au-
tomaton and Young diagrams, but what are the counterparts of simple paths?
Can they be “found” in this lattice? Not quite – we need to look at Young
tableaux as opposed to just Young diagrams. We will illustrate that the sim-
ple paths of the automaton of an increasing pattern τ
correspond to chains
in the set of all Young tableaux on [∅,λ
,k−
] in Example 7.53. To assist with
© 2010 by Taylor and Francis Group, LLC
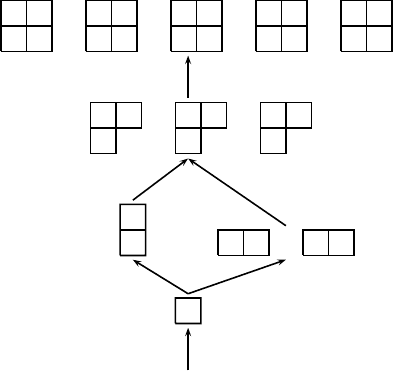
Automata and Generating Trees 273
this task, Figure 7.13 shows the Young tableaux associated with each of the
Young diagrams corresponding to the automaton A(123, 4). For the proof of
this bijection, see Stanley [183, Chapter 7].
4
3
2
1
4
2
3
1
3
2
3
1
2
1
2
1
3
1
2
1
1
2
12
3
13
2
1
2
1
1121
1
∅
ε
2
1
23
13
12
FIGURE 7.13: Young tableaux contained in the shape λ
2,2
.
Example 7.53 We will describe how the Young tableaux given in Figure 7.13
correspond to simple paths in the automaton. Each state is associated with a
specific Young diagram, which in turn has several associated Young tableaux.
For each such Young tableau corresponding to a given state, the largest element
in the tableau indicates the length of the simple path from ε to that state. For
example, the Young diagram (2, 1) corresponds to the state 13 (see Figure
7.12). There are three associated Young tableaux, namely those filled with 132,
123 and 112 (where the fillings are always from top to bottom and from left to
right in the given order).
For the first one, looking at the filling we can see that the tableau was
successively created by the sequence of tableaux with fillings 1(corresponds to
2), 12 (corresponds to 23), and finally 132. Therefore the Young tableau
with filling 132 corresponds to the simple path ε→2→23→13
of length three, the maximal element in the Young tableau with filling 132.
On the other hand, the Young tableau 11 corresponding to the state 1 has
maximal entry one, so state 1 was reached directly from ε, and therefore,
the Young tableau 112 corresponds to the simple path of length 2 given by
© 2010 by Taylor and Francis Group, LLC

274 Combinatorics of Compositions and Words
ε→1→13.
In addition, the longest simple paths correspond to those Young tableaux
that fill the shape λ
2,2
completely and also contain all possible values. These
tableaux correspond to a diagram that is the largest element in the Young
lattice, and therefore, the length of the longest simple path equals the length
of the maximal chain in the Young lattice.
We now give the alternative proof of Regev’s result:
Theorem 7.54 [169, Theorem 1] For all k ≥ we have
AW
τ
[k]
(n) ≈ C
,k
n
(k−)
n
(as n →∞),
where C
−1
,k
=
(k−)
i=1
k−
j=1
(i + j − 1).
Proof By Lemma 7.40 each state except τ
has loops. Thus Corollary
7.38 applies and we have that
AW
τ
[k]
(n)=
M
j=0
a
j
n−j
n
j
,
where a
j
counts the number of simple paths of length j in A(τ
,k)andM
is the maximal number of states (since all have loops) in a simple path.
From the proof of Theorem 7.51 we have that the maximal simple paths
in the automaton correspond exactly to the maximal chains in the Young
lattice [∅,λ
,k−
]. The length of the maximal chains in [∅,λ
,k−
]isgivenby
M = (k − ). Since the dominant term with regard to the limiting behavior
is the one with the highest power, M, we obtain that
AW
τ
[k]
(n) ≈ a
M
−M
n
M
n
≈
a
M
M!
−M
n
M
n
(n →∞),
where a
M
is equal to the number of maximal chains in J([] ×[k −]). Using
results on maximal chains in J([] ×[k −]) [183, Proposition 7.10.3] and the
hook-length formula [183, Corollary 7.21.6] we have that
a
(k−)
=
((k − ))!
i=1
k−
j=1
(i + j − 1)
,
which gives the desired result. 2
For the moment, we will leave asymptotics behind. However, we will draw
on what we have derived so far to obtain an exact result for the special case of
© 2010 by Taylor and Francis Group, LLC
