Heubach S., Mansour T. Combinatorics of Compositions and Words
Подождите немного. Документ загружается.

Automata and Generating Trees 255
ε
FIGURE 7.6: Automaton for tilings that are indecomposable.
or compositions) should be considered the “same” if the pattern of interest
will occur or be avoided equally in both sequences when appending any letter
to the sequences. We first consider words, and later modify the approach for
compositions.
Definition 7.25 For k>0,let[k]
∗
=
$
n
[k]
n
be the set of all finite words
on the alphabet [k],andletτ be a subsequence pattern. For fixed k and τ,two
words v, w ∈ [k]
∗
are equivalent on [k]
∗
, denoted by v
A
∼ w, if for all words
r ∈ [k]
∗
we have
vr avoids τ ⇔ wr avoids τ,
where vr denotes the concatenation of the words v and r. Wedenotethe
equivalence class of a word w by w,anduseAW
[k]
∗
(τ) to denote the set of
words in [k]
∗
that avoid τ.
Such an equivalence is sometimes called the Nerode equivalence [101].
Example 7.26 Let τ = 132, k ≥ 4, v =13and w =14.Thenv
A
w,since
133 avoids τ,but143 contains τ.
At first sight it may seem difficult to determine if v
A
∼ w, since a priori there
are an infinite number of words r ∈ [k]
∗
to be checked. However, Lemma 7.27
(originally shown by Br¨and´en and Mansour [27]) saves us, as it ensures that
we have to check only finitely many words r.
Lemma 7.27 Let τ be a pattern of length and let v, w ∈ [k]
∗
be any two
words. Then v
A
∼ w if and only if for all words r ∈ [k]
s
with 0 ≤ s ≤ we
have that vr avoids τ ⇔ wr avoids τ.
© 2010 by Taylor and Francis Group, LLC
256 Combinatorics of Compositions and Words
Proof Define an equivalence relation
A
∼
on [k]
∗
by: v
A
∼
w if for all words
r ∈ [k]
s
,0≤ s ≤ ,wehavethatvr avoids τ ⇔ wr avoids τ. Clearly, v
A
∼ w
implies v
A
∼
w. Now assume that v
A
∼
w, but v
A
w. Without loss of
generality, we may assume that there is an r ∈ [k]
∗
such that vr contains τ
and wr avoids τ. Any occurrence of τ in vr can use at most letters of r.
Thus, there is a subsequence r
of r of length at most such that vr
contains
τ and wr
avoids τ,thatis,v
A
w, a contradiction. 2
We can now define the automaton for pattern avoidance in words.
Definition 7.28 Given a positive integer k and a subsequence pattern τ,we
define the finite automaton A(τ,k)=(E(τ,k), [k], Δ, ε, E(τ, k)\{τ}),where
E(τ,k) is the set of the equivalence-classes of
A
∼, Δ(w,i)=wi,andε is
the empty word.
Definition 7.29 We identify A(τ,k) with the directed graph G
A
that has
vertices E(τ,k)\{τ} and a (labeled ) edge
i
−→ between v and w if vi
A
∼ w.
Multi-edges between two vertices are combined by placing their respective labels
on a single edge connecting the two vertices. We call a path in G
A
simple if it
starts in ε, does not use any loops, and does not end in τ. The associated
adjacency matrix A(τ,k) of A(τ,k) of size (|E(τ,k)|−1) × (|E(τ,k)|−1) is
defined by
A(τ,k)
ij
= |{s ∈ [k]:Δ(x
i
,s)=x
j
}|,
that is, A(τ,k)
ij
counts the number of edges between x
i
and x
j
.
Note that we omit the state τ in the associated graph in the context of
pattern avoidance, so the associated graph consists of only accept states. Is
there any effect of this choice on the count of the number of words avoiding
τ? The answer is no: the state τ is irrelevant, as we are never interested
in paths that pass through or end in the equivalence class τ. Therefore, we
are permitted to disregard this state for the purpose of counting the number
of words avoiding τ. This is quite different from the automaton we built in
Example 7.24, where almost all paths passed through nonaccept states to the
accept state. There, deletion of nonaccept states would not be possible.
In addition, in the setting of avoidance of subsequence patterns, we can
list the states in canonical order,thatisasx
1
, x
2
,...,x
e
in such a way
that for i<jthere is no path from x
j
to x
i
.Whyisthatso?When
appending a letter from the alphabet, either the letter is relevant, in which
case we create a new state, or the letter added is not relevant, in which case
we have a loop. In fact, we claim that the automaton graph has only loop
paths and paths. Assume there was a cycle, for example x
1
i
→x
2
j
→x
1
.
This would imply that wij
A
∼ w, in which case the letter i cannot have been
© 2010 by Taylor and Francis Group, LLC
Automata and Generating Trees 257
relevant and therefore wi
A
∼ w,andx
1
i
x
2
. Thus, the graph has no cy-
cles, which implies that we can find a canonical order for the states. However,
the above argument for the absence of cycles works only for avoidance of sub-
sequence patterns, not for generalized or subword patterns where adjacency
requirements come into play and may result in cycles.
We start by deriving the automaton for avoidance of the (subsequence)
pattern 123 in words on the alphabet [4].
ε
1
2
12
13
23
1
2
2
3
1
3
1
3, 4
1, 4
1, 2
1, 3
2, 3
2, 4
2
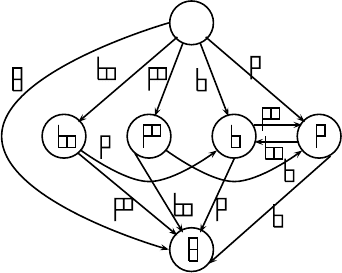
FIGURE 7.7: Final states in the automaton A(123, 4).
Example 7.30 Let τ = 123. Then in any word that starts with a 3 or a 4,
the first letter cannot be part of an occurrence of τ, and therefore, such a word
is equivalent to ε. However, a first letter 1 or 2 can be part of an occurrence
of τ, leading to two new equivalence classes, 1 and 2. For both of these
states, appending a 4 cannot create a pattern τ. Likewise, appending i to i
(a repeated letter, but τ has no repeated letters) is irrelevant, and therefore,
i4
A
∼ i and ii
A
∼ i.
Now let’s look at the other two possibilities for 1. Appending either a 2
or a 3 leads to the new equivalence classes 12 and 13 (since 123
A
133).
Next we look at 2 and claim that 21
A
∼ 1. Why? Let’s think in terms
of occurrence of the pattern τ. If the occurrence of τ involves the 2 as the
smallest part, then the 1 will also create a pattern τ. The other possibility is
an occurrence of τ that does not involve the 2, but starts with the 1. Therefore,
Δ(2, 1) = 1. The last case, appending the letter 3 to 2 leads to a new
class, 23. We repeat the analysis for the states whose labels have two letters.
Clearly, Δ(ij,i)=Δ(ij,j)=ij,andfori =3, 4, Δ(12,i)=123
(which is not displayed in the graph). Likewise, Δ(i3, 4) = 123 for i =1, 2.
© 2010 by Taylor and Francis Group, LLC
258 Combinatorics of Compositions and Words
The same argument that showed that Δ(2, 1) = 1 gives that Δ(13, 2) =
12.Finally,Δ(23, 1) = 13 follows from the definition of the equivalence.
Figure 7.7 shows the graph G
A
.
Let’s now look at the associated adjacency matrix. As a convention, we will
order the states as follows (if this results in a canonical order): according to
the length of their label in increasing order, and among the states with labels
of the same length in such a way that the edge (i, j)onlyexistsfori ≤ j.
Example 7.31 (Continuation of Example 7.30) Using the canonical ordering
ε, 2, 1, 23, 13,and12, the first three powers of the associated
adjacency matrix A = A(123, 4) are given by
A =
⎡
⎢
⎢
⎢
⎢
⎢
⎢
⎣
211000
021100
002011
000210
000021
000002
⎤
⎥
⎥
⎥
⎥
⎥
⎥
⎦
,A
2
=
⎡
⎢
⎢
⎢
⎢
⎢
⎢
⎣
445111
044421
004045
000441
000044
000004
⎤
⎥
⎥
⎥
⎥
⎥
⎥
⎦
, and A
3
=
⎡
⎢
⎢
⎢
⎢
⎢
⎢
⎣
81218 6 8 8
0 8 12 12 12 8
0 0 8 0 12 18
0008126
0000812
000008
⎤
⎥
⎥
⎥
⎥
⎥
⎥
⎦
.
The relevant entries are the elements in the first row of the respective matrix.
They correspond to the number of ways to go from the start state (empty word )
to any state in a given number of steps. Summing the entries of the first row
of A
n
therefore gives AW
123
[4]
(n), the total number of words of length n on the
alphabet [4] avoiding the pattern 123.Thus,
AW
123
[4]
(1)=2+1+1=4,
AW
123
[4]
(2)=4+4+5+1+1+1=16, and
AW
123
[4]
(3)=8+12+18+6+8+8=60.
No surprise here – for n =1or n =2the pattern 123 cannot occur, and for
n =3, there are exactly four words that contain 123, namely the words 123,
124, 134,and234.
We give a second example of an automaton, this time for avoidance of the
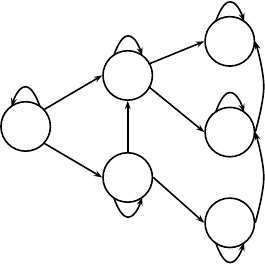
pattern τ = 122 in words on the alphabet [3]. Figure 7.8 shows the graph
corresponding to the automaton A(122, 3).
Comparing the graphs in Figures 7.7 and 7.8, we see similarities and dif-
ferences between the two graphs. The most notable difference is that the
automaton A(122, 3) has a state that has a label with three letters, while the
graph of A(123, 4) has labels with at most two letters, even though in both
cases the pattern to be avoided is of length three. On the other hand, the two
graphs have in common that in each graph all states have the same number
of loops (two loops for A(123, 4) and one loop for A(122, 3)). In Section 7.3.3
we will prove that this is always the case for automata of words avoiding an
increasing pattern τ
=12···( +1).
© 2010 by Taylor and Francis Group, LLC
Automata and Generating Trees 259
ε
1
2
12
13
23
123
1
2
2
3
1
3
1
2
3
3
1
1
1
1
2
2
FIGURE 7.8: The graph of the automaton A(122, 3).
We know much less about the structure of automata for avoidance of pat-
terns with repeated letters in words. Mansour developed a C++ program,
TOU
AUTO, which computes the equivalence classes and the adjacency ma-
trix for the automaton of a subsequence pattern τ. The program TOU
AUTO
is listed in Appendix G.5 and is also available on Mansour’s home page [139]
for use by the readers. Using this program, we can obtain the adjacency
matrices for the automata A(1132, 4) and A(1312, 4), respectively, as
⎡
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎣
211000000000
020110000000
002011000000
000200110000
000120001000
000002001100
000000210000
000000020000
000100002010
000000000210
000000000021
000000010002
⎤
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎦
and
⎡
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎣
211000000000000000
0 1 0111000000000000
002100100000000000
000200011000000000
00001 1010100000000
000002000011000000
000000200000110000
000000021100000000
000000002010001000
000000000200000100
000000000020000000
000000001012000000
0000000010001 00011
000000000000020010
000000000010002000
000000000010000200
000000000000001020
000000001100001001
⎤
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎦
.
© 2010 by Taylor and Francis Group, LLC

260 Combinatorics of Compositions and Words
Note that the automaton for the pattern 1312 has two types of states, those
with one and those with two loops.
As mentioned before, we can also use the program TOU
AUTO to obtain
the states of the automata for each of the permutation patterns of length
three for different values of k. Table 7.1 lists the states of the automaton
A(τ,k)whenτ ∈S
3
and k =3, 4. For the corresponding equivalence classes
for k =5,see[27].
TABLE 7.1: States of the automaton A(τ,k)forτ ∈S
3
k τ The equivalences classes in E(p, k)
3 123 ε, 1, 12, 123
132 ε, 1, 13, 132
213 ε, 2, 21, 213
231 ε, 2, 23, 231
312 ε, 3, 31, 312
321 ε, 3, 32, 321
4 123 ε, 1, 2, 12, 13, 23, 123
132 ε, 1, 2, 13, 14, 24, 132, 241
213 ε, 2, 3, 21, 23, 31, 32, 213
231 ε, 2, 3, 23, 24, 32, 34, 231
312 ε, 3, 4, 31, 41, 42, 312, 314
321 ε, 3, 4, 32, 42, 43, 321
In light of the previous examples and Table 7.1, several questions about the
structure of the automaton graphs arise:
1. From Table 7.1 we see that patterns in the same Wilf-equivalence class
can have a different number of states, which implies that the respective
graphs are not isomorphic. However, patterns that are complements of
each other, and patterns that are the reverse of each other have the
same number of states. So the questions are:
• Since w avoids τ if and only if R(w)avoidsR(τ), are the automata
A(τ,k)andA(R(τ),k) always isomorphic?
• Since w avoids τ if and only if c(w)avoidsc(τ), are the automata
A(τ,k)andA(c(τ),k) always isomorphic?
2. Since the number of paths of length n in a graph is given by the ele-
ments of the n-th power of its adjacency matrix, can we obtain exact or
asymptotic results (as n →∞) from the adjacency matrix?
3. What kind of structural results are there for families of patterns, specif-
ically the increasing patterns?
© 2010 by Taylor and Francis Group, LLC

Automata and Generating Trees 261
The first question is the easiest to answer. From the definition of
A
∼ it
is clear that A(τ,k)andA(c(τ),k) are isomorphic as automata (replace the
state s by c(s) and the edge j by c(j)). This is generally not the case
for A(τ, k)andA(R(τ),k). Indeed, using the program TOU
AUTO, Br¨and´en
and Mansour [27] found that for τ = 2314 and k =5wehave|E(2314, 5)| =13
and |E(4132, 5)| = 14. For an example where the number of states is the same,
but the automata are not isomorphic, see Exercise 7.2.
Before answering the remaining questions, we give another example, the
automaton for avoiding τ = 3241 in words on the alphabet k =5. Notethat
the adjacency matrix given by the program TOU
AUTO may correspond to
states not listed in canonical order (if i<j, then there is no path from x
j
to x
i
), so the matrix is not necessarily upper triangular.
Example 7.32 If τ = 3241 and k =5, then the accept states are ε, 3,
4, 32, 34, 42, 43, 324, 325, 342, 432, 435,and3243.The
automaton A(3241, 5) has adjacency matrix
A(3241, 5) =
⎡
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎣
3110000000000
0301100000000
0030011000000
0003000110000
0000301001000
0000031100000
0000003000110
0000000300001
0000000130000
00000002 0 2 100
0000000000311
0000000000030
0000000000013
⎤
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎦
.
N
ote that almost all states in A(3241, 5) have three loops, with the exception
of 342, which has two loops. In addition, there is a multi-edge between 342
and 324,namely342
2,4
−→ 324.
We will now tackle the second question posed above, namely obtaining
results on AW
τ
[k]
(n) from the adjacency matrix. This is achieved by using the
transfer matrix method, which can be used to obtain asymptotic results as
well as explicit ones, with the asymptotic results usually easier to derive. The
third question will be answered in Section 7.3.3.
7.3.2 Transfer matrix method
The transfer matrix method uses the adjacency matrices of graphs for enu-
meration in combinatorics. The main idea is to express the generating function
© 2010 by Taylor and Francis Group, LLC
262 Combinatorics of Compositions and Words
for a sequence {a
n
} in terms of the adjacency matrix of an associated graph.
To apply this approach, one has to construct a bijection between the objects in
question and walks in an appropriate edge-weighted directed multi-graph. We
state the general result, which will also be used in Section 7.4 for generating
trees.
Theorem 7.33 [182, Theorem 4.7.2] Consider an edge-weighted directed mu-
lti-graph G on p vertices v
1
,...,v
p
,andletA denote its weighted adjacency
matrix, that is, a
ij
is the total weight of the edges from v
i
to v
j
. Then the
generating function for the total weight of walks from v
r
to v
s
is given by
n≥0
(A
n
)
r,s
x
n
=(I − xA)
−1
r,s
=
(−1)
r+s
det(I − xA:s, r)
det(I − xA)
, (7.1)
where I is the identity matrix and det(B : s, r) is the minor of B obtained
when removing row s and column r. In particular, the generating function is
a rational function of x whose degree is strictly less than the multiplicity n
0
of the value 0 as an eigenvalue of A.
Proof Let F
ij
(A, x)=
n≥0
(A
n
)
ij
x
n
=(I −xA)
−1
ij
. From Theorem B.12,
we have that
F
ij
(A, x)=
(−1)
i+j
adj(I −xA)
ij
det(I −xA)
,
which gives the desired result for the generating function. To show the claim
about the degree of the generating function, suppose that A is a p ×p matrix
and that n
0
is the multiplicity of the eigenvalue 0. Then λ
n
0
is a factor of the
characteristic polynomial (see Definition B.20) and
det(λI −A)=a
p−n
0
λ
n
0
+ ···+ a
1
λ
p−1
+ λ
p
.
Thus by Theorem B.17, Part 1,
det(I − xA)=x
p
det
1
x
I − A
= a
p−n
0
x
p−n
0
+ ···+ a
1
x +1,
which implies that as polynomials in x,
deg(det(I −xA)) = p −n
0
and deg(det(I − xA : j, i)) ≤ p − 1.
Hence, deg F
ij
(A, x) ≤ p − 1 − (p − n
0
) <n
0
, as claimed. 2
Since the generating function is a rational function whose maximal degree
is bounded by a computable quantity (namely the degree of the matrix A),
it can be used to derive asymptotic results. Theorem 7.34 is a version of
Theorem 7.33 specific to automata.
© 2010 by Taylor and Francis Group, LLC

Automata and Generating Trees 263
Theorem 7.34 Let k ∈ N, τ be a pattern, e
k
be the number of states in
A(τ,k),andletA(τ,k) be the adjacency matrix of the graph G
A
with the
states in canonical order. Then the generating function for AW
τ
[k]
(n) is given
by
AW
τ
[k]
(x)=
e
k
−1
j=1
(−1)
1+j
det(I −xA:j, 1)
e
k
−1
i=1
(1 −
i
x)
, (7.2)
where
i
is the number of loops at state v
i
,ande
k
= |E(τ,k)|. If the states
are not in canonical order, then the denominator is the product of the eigen-
values of (I −xA).
Proof This follows immediately from Theorem 7.33 since we want to count
the number of paths of length n from ε to any state other than τ in
A(τ,k). Since the states are in canonical order, A is a triangular matrix and
its determinant is given by the product of the entries on the diagonal. 2
We will next find the exact asymptotics (up to a constant) for AW
τ
[k]
(n)for
all patterns τ. The following simple lemma given in [27], which tells us about
the number of loops, will be helpful in finding the asymptotic growth of the
sequence AW
τ
[k]
(n)forfixedk and τ.
Lemma 7.35 Let A(τ,k) be an automaton, d be the number of distinct letters
in τ, and suppose that k ≥ d − 1.Ifv is any state different from τ,then
the number of loops at v does not exceed d − 1. Moreover, there are exactly
d − 1 loops at ε.
Proof Suppose that there are more than d − 1loopsatv for v
A
τ.
Then the loops use at least d different edge labels. From these labels we can
form a word w that is order-isomorphic to τ.Butthenvw
A
∼ v which is a
contradiction. To show the second statement, let τ
1
be the first letter of τ.
Then, for i<τ
1
or i>k−d + τ
1
,wehavei
A
∼ ε.Butthereared −1suchi’s,
which proves the lemma. 2
To express how a sequence behaves for large values of n,weusethefollowing
notation.
Definition 7.36 For two sequences {a
n
} and {b
n
} of real numbers, we write
a
n
≈ b
n
if lim
n→∞
a
n
b
n
=1.Ifa
n
≈ K
n
for fixed K, then we say that {a
n
} is
of exponential order K
n
.
We can now state the asymptotics for any pattern τ with d letters.
© 2010 by Taylor and Francis Group, LLC

264 Combinatorics of Compositions and Words
Theorem 7.37 Let τ be any pattern with d distinct (but possibly repeated )
letters and let k ≥ d − 1 be given. Then there is a constant C>0 such that
AW
τ
[k]
(n) ≈ Cn
M
(d − 1)
n
(n →∞),
where M +1 is the maximum number of states with d −1 loops in any simple
path.
Proof Let P = v
1
v
2
···v
j
be a simple path in A(τ,k)oflengthj −1. Then
AW
τ
[k]
(n)=
P
N(P, n), where N(P, n) is the number of paths of length n
associated with the simple path P of length j − 1with1≤ j ≤ n +1. Each
simple path of length j − 1 can be extended to a walk of length n by passing
through a total of n − j +1 ofthe loops. Let
i
be the number of loops at
vertex v
i
,andα
i
be the number of loops the walk passes through at vertex
v
i
.Then
N(P, n)=
α
1
+···+α
j
=n−j+1
α
1
1
α
2
2
···
α
j
j
, (7.3)
where the sum is over all weak (α
i
≥ 0) compositions of n −j +1 into j parts.
Since N(P, n) is a convolution, the associated generating function is a product
of geometric series, and therefore N(P, n)=[t
n−j+1
](1−
1
t)
−1
···(1−
j
t)
−1
.
Let r be the number of indices i such that
i
= d −1. Note that by Lemma
7.35, r is greater than or equal to one. Using partial fraction decomposition,
we obtain that the dominant term of (1 −
1
t)
−1
···(1 −
j
t)
−1
is equal to
f(t)
(1 − (d − 1)t)
r
,
where f(t) is a polynomial of degree less than r and f ((d − 1)
−1
) =0. By
well known results from complex analysis (see Appendix E and Chapter 8)
it follows that N (P, n) ≈ C(P )(d − 1)
n
n
r−1
,whereC(P ) > 0isaconstant
that depends on P and k. Summing over all paths and taking limits, only the
contribution of the paths with maximal r “survives.” 2
If every state except τ in A(τ, k) has exactly d − 1 loops, then it follows
from Equation (7.3) that AW
τ
[k]
(n)=(d −1)
n
Q(n), where Q is a polynomial
in n. We have in fact the following result.
Corolla ry 7.38 Let τ be a pattern with d distinct letters and let A(τ,k) be
an automaton where all states but τ have exactly d − 1 loops. Then
AW
τ
[k]
(n)=
M
j=0
a
j
(d − 1)
n−j
n
j
,
where a
j
counts the number of simple paths of length j in A(τ,k). Moreover,
if τ is a pattern of length +1,thena
i
=(k − d +1)
i
for all i =0, 1,...,.
© 2010 by Taylor and Francis Group, LLC
