Heubach S., Mansour T. Combinatorics of Compositions and Words

Подождите немного. Документ загружается.



Mathematica

Maple

is a registered trademark of Waterloo Maple Software.

Mathematica is a registered trademark of Wolfram Research, Inc.

Mathematica

http://math.haifa.ac.

il/toufik/manbook.html

sheubac@calstatela.edu toufik@math.haifa.il

Skype

is a registered trademark of Skype Limited.

Dis-

crete Mathematics Integers Ars Combinatoria Journal of Diﬀerence

Equations and Applications

Discrete Mathematics Discrete Applied Mathe-

matics Advances in Applied Mathematics Journal of Integer Sequences

Journal of Combinatorial Theory Series A Annals of Combinatorics

Electronic Journal of Combinatorics

Chapter 1

Introduction

1.1 Historical overview – Compositions

P.A. MacMahon

The study of compositions has a long and rich history.

The earliest publication on compositions is by Percy

Alexander MacMahon

(1854 – 1929) in 1893, entitled

Memoir on the Theory of Compositions of a Number

[136], which appeared in the Philosophical Transactions

of the Royal Society of London. At the time, articles

were submitted and read before the society prior to be-

ing published. MacMahon begins the memoir by stat-

ing that “Compositions are merely partitions in which

the order of occurrence of the parts is essential,” and

then proceeds to give the partitions and compositions

of n = 3 as an example.

This more informal style of writing was quite common in the papers at the

time, where deﬁnitions, examples, statements and proofs followed each other

without much of the formal structure one sees in today’s papers. Therefore,

when quoting results given by MacMahon, we will indicate the page on which

the statement appears.

Deﬁnition 1.1 A partition of a positive integer n is a nonincreasing sequence

p = p

...p

of positive integers such that



i=1

= n.Acomposition of

a positive integer n is any sequence σ = σ

...σ

of positive integers such

that



i=1

= n.Thep

and σ

are called the parts,andpar(p)=m and

par(σ)=m denote the number of parts of the partition and composition,

respectively. We refer to n as the order of the partition or composition and

denote it by ord(p) and ord(σ).

http://www-history.mcs.st-andrews.ac.uk/Mathematicians/MacMahon.html

http://en.wikipedia.org/wiki/Percy Alexander MacMahon

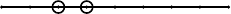
2 Combinatorics of Compositions and Words

Note that the diﬀerence between partitions and compositions is a matter

of order – for partitions we do not care about order, while for compositions,

two diﬀerently ordered sequences result in two diﬀerent compositions of n.

Thus for every partition with at least two diﬀerent parts, there are more

compositions than partitions, as we can reorder the partition in all possible

ways to get the associated compositions.

Example 1.2 The partitions of 4 are 4, 31, 22, 211 and 1111,whilethe

compositions of 4 are 4, 31, 13, 22, 211, 121, 112 and 1111. The partition

211 can be reordered in three diﬀerent ways and results in the compositions

211, 121, 112. However, the partition 22 results in only one composition 22.

MacMahon derived a number of results, for example the total number of

compositions and the number of compositions with a given number of parts,

using generating functions. He also provided a representation of a composition

as a graph, which allowed for the derivation of those results using a simple

combinatorial argument. As deﬁned by MacMahon, “the graph of a number

n is taken to be a straight line divided at n − 1 points into equal segments.

The graph of a composition of the number n is obtained by placing nodes at

certain of the n − 1 points of division.” Figure 1.1 illustrates the graph of

the composition 215 of eight in the format given in [136]. We refer to this

representation as the line graph of a composition to distinguish it from other

representations that will be introduced in Chapter 3.

APQ B

FIGURE 1.1: Line graph of the composition 215.

The individual parts are read oﬀ as the number of segments between nodes

or between the ﬁrst and the last nodes and the endpoints A and B, respec-

tively. Using this representation, MacMahon gave a combinatorial proof of

the following result.

Theorem 1.3 [136, page 835] The number of compositions of n with exactly

m parts is given by



n−1

m−1



, and the total number of compositions of n is 2

n−1

Proof Since the number of parts of a composition is one more than the

number of nodes, and the number of division points is n −1, we merely select

at which of the n −1 division points we place the m −1 nodes. Furthermore,

since each of the n − 1 division points is either a node or not a node in each

composition, the total number of compositions is 2

n−1

. 2