Heubach S., Mansour T. Combinatorics of Compositions and Words

Подождите немного. Документ загружается.

Introduction 3

MacMahon also looked at relationships between compositions, for example

conjugate and inverse compositions.

Deﬁnition 1.4 Two compositions of n are conjugate if in their respective

line graphs, one has nodes exactly at the positions where the other one does

not have nodes and vice versa. We denote the conjugate of σ by conj(σ).

Figure 1.2 shows the line graphs of two conjugate compositions. Note that

it is very easy to derive the conjugate composition using the line graph, but

that an algorithmic description of how to compute a conjugate composition

without the line graph is quite lengthy (see [136, pages 837-838]) and much

less obvious.

FIGURE 1.2: Line graphs of conjugate compositions 215 and 131111.

Deﬁnition 1.5 If σ = σ

...σ

,thenitsinverse or reverse composition

is given by R(σ)=σ

m−1

...σ

. A composition is called self-inverse or

palindromic if it reads the same from left to right as from right to left. A

composition is called reverse conjugate if the reverse of σ is also the conjugate

of σ.

Example 1.6 The palindromic compositions of 4 are 4, 22, 121,and1111,

none of which are reverse conjugate.

MacMahon enumerated palindromic compositions and gave several results

involving conjugate compositions. The remainder of his memoir is devoted to

connections of generalized compositions and partitions, including line graphs

for these more general compositions.

In the years that followed the publication of his memoir [136], the main

focus of research in enumerative combinatorics was on partitions and permu-

tations, driven in part by MacMahon’s proliﬁc writing. Until the late 1960s,

individual articles on various aspects of compositions appeared, but there was

no concentrated research interest. This was followed by roughly a decade in

which several groups of authors developed new research directions in com-

positions. They studied compositions that were restricted in some way, and

not only enumerated the total number of these compositions, but also cer-

tain characteristics, or statistics, for example rises, levels, and drops, of these

compositions. However, the majority of publications on compositions has

been within the last decade, when many diﬀerent authors have studied vari-

ous aspects of compositions, generalizing papers from the 1970s, introducing

new types of compositions, or extending research questions and methods for

pattern avoidance in permutations to compositions. Another focus was the

4 Combinatorics of Compositions and Words

study of random compositions to obtain asymptotic results, that is, the rate

of growth for the quantities of interest as n tends to inﬁnity. Tables 1.1, 1.2

and 1.3 give an overview of research activity for compositions over time in

ﬁve major areas: restrictions on the set from which the parts can be chosen,

restrictions on the arrangements of parts within the composition, enumera-

tion of statistics of compositions in N, pattern avoidance in compositions, and

asymptotic results based on methods from complex analysis and probability

theory. Papers that do not fall into one of these areas are listed under vari-

ations on compositions, and we will brieﬂy indicate the areas studied here.

Research in the ﬁve major areas will be described in more detail in Section 1.3.

Note that we use † to denote articles that have multiple authors, and that we

have abbreviated a few authors’ names to ﬁt the information into the table.

In particular, Knopfmacher is shortened to Knop., Srini. refers to Srinivase

Rao, and Serv. refers to Servedio.

Table 1.1 shows the time line from 1893 to 1982, which includes the decade

when Hoggatt, Carlitz and their co-authors were very active.

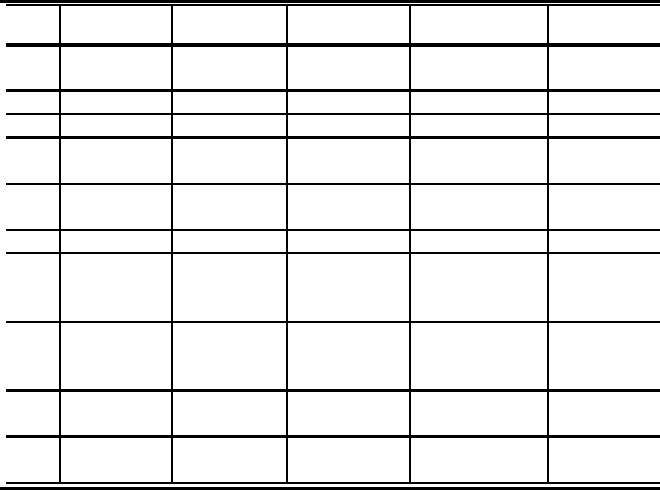
TABLE 1.1: Time line of research in major areas for compositions

Year Restricted Restricted Statistics Variations

sets arrangements

1893 MacMahon [136]

1955 Narayana [161]

1958 Narayana

†

[162]

1964 Gould [74]

1965 Mohanty [155]

1967 Mohanty [156]

1968 Hoggatt

†

[99]

1969 Hoggatt

†

[100]

1975 Alladi

†

[7] Hoggatt

†

[98] Abramson [1]

1976 Carlitz

†

[38] Abramson [2]

1977 Carlitz [39]

1978 Carlitz [40]

1982 Cerasoli [45]

Charalambides [46]

Of the papers listed under variations, there was a cluster in the 1950s and

1960s. Narayana and Mohanty independently studied domination of com-

positions [155, 156, 161], Narayana and Fulton investigated the structure of

compositions as a distributive lattice [162], and Gould found an identity that

involves binomial coeﬃcients, the bracket function and compositions with rela-

Even though title or paper refers to partitions, it is compositions that are studied

Introduction 5

tively prime parts [74]. In 1982, Cerasoli [45] and Charalambides [46] provided

connections between compositions and important number sequences.

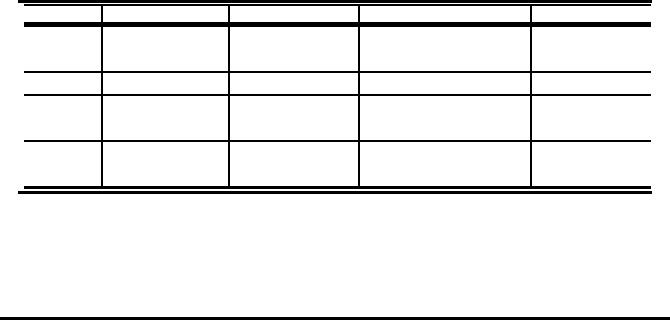
TABLE 1.2: Time line of research in major areas for compositions

Year Restricted Restricted Statistics Asymptotics Variations

sets arrangements

1995 Richmond

†

[171] Serv.

†

[178]

Zanten [188]

1997 Hwang

†

[102]

1998 Knop.

†

[119]

1999 Knop.

†

[118] Hitczenko

†

[95]

Knop.

†

[117]

2000 Grimaldi [76] Rawlings [168] Hitczenko

†

[97] Agarwal [3]

Srini.

†

[181]

2001 Grimaldi [77] Hitczenk o

†

[93]

2002 Goh

†

[73]

Hitczenko

†

[94]

Louc hard

†

[134]

2003 Chinn

†

[50] Chinn

†

[48] Louc hard[133] Agarwal [4]

Chinn

†

[51] Heubach

†

[87] Knop.

†

[120]

Chinn

†

[52]

2004 Heubach

†

[89] Bender

†

[20] Corteel

†

[56]

Merlini

†

[154] Hitczenko

†

[96]

2005 Heubach

†

[90] Knop.

†

[121] Bender

†

[19]

Corteel

†

[57]

In 1995, the ﬁrst papers on asymptotics for compositions appeared. Tables

1.2 and 1.3 give the time line from 1995 to the present. Here, the variations

on compositions mostly result from new types of restrictions on compositions,

with the exception of the papers by van Zanten [188], who connected compo-

sitions with Gray codes, and Servedio and Yeh [178], who studied the coloring

of circular-arc graphs which leads to circular compositions. Corteel and her

co-authors [56, 57] studied compositions where the i-th part satisﬁes a sys-

tem of linear inequalities in the parts that follow the i-th part. The authors

gave generating functions that can be computed from the coeﬃcients of the

linear inequalities. Bender and Canﬁeld [19] considered compositions of n

in which the ﬁrst part, the last part, and the diﬀerences between adjacent

parts all lie in prescribed sets. Under quite general conditions, the number of

such compositions is determined asymptotically. In addition, the number of

parts, rises, falls, and various other statistics are shown to satisfy a central

limit theorem. Finally, Jackson and Ruskey [103] found interesting connec-

tions between meta-Fibonacci sequences and compositions in which the i-th

coeﬃcient is in a speciﬁed set.

6 Combinatorics of Compositions and Words

Other types of compositions do not stem from restricting the compositions,

but from introducing characteristics that can be translated into a coloring of

the individual parts. Examples are the n-color compositions introduced by

Agarwal, where the part n occurs in n colors [3, 4]. Narang and Agarwal [159,

160] studied n-color self-inverse compositions and connections between lattice

paths and n-color compositions. Another variation is the cracked compositions

discussed in Chapter 3, or the compositions that have two types of 1s, but

only one type of any other part studied by Grimaldi [79]. He enumerated

for example the total number of summands and derived connections with the

alternate Fibonacci sequence.

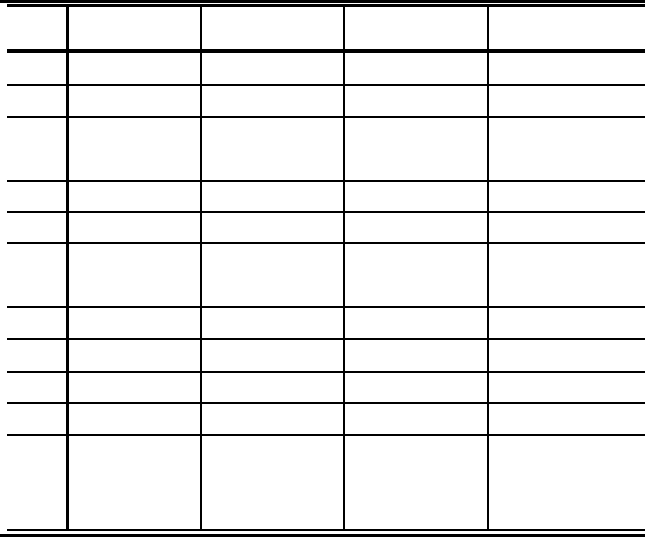
TABLE 1.3: Time line of research in major areas for compositions

Year Statistics Asymptotics Pattern avoidance Variations

2006 Kitaev

†

[111] Heubach

†

[91] Narang

†

[159]

Mansour

†

[145] Savage

†

[176] Jackson

†

[103]

2007 Heubach

†

[92] Heubach

†

[88] Grimaldi [79]

2008 Jel´ınek

†

[105] Narang

†

[160]

Baril

†

[17]

2009 Brennan

†

[28]

Knop.

†

[115]

1.2 Historical overview – Words

We now turn our attention to words. The origins of research activity for

words are a little harder to pin down because they arise naturally in many

diﬀerent settings, for example in group theory to describe algebras, in proba-

bility theory to describe coin-tossing experiments and in computer science in

the context of automata (see Chapter 7) and formal languages.

Deﬁnition 1.7 Let [k]={1, 2,...,k} be a (totally ordered) alphabet on k

letters. A word w of length n on the alphabet [k] is an element of [k]

and

is also called word of length n on k letters or k-ary word of length n. Words

with letters from the set {0, 1} are called binary words or binary strings.

Example 1.8 The words of length three on two letters are 111, 112, 121,

122, 211, 212, 221 and 222, while the binary strings of length two are given

by 00, 01, 10,and11.

Introduction 7

Basic results such as the total number of words were part of well-known

mathematical folklore long before a systematic study of their properties was

undertaken.

Lemma 1.9 The number of k-ary words of length n is given by k

Proof There are k choices for the ﬁrst letter, and for any choice of the ﬁrst

letter, there are k choices for the second letter, for a total of k

choices for

the ﬁrst two letters. By the same argument, there are k

words of length 3,

andingeneral,k

words of length n over the alphabet [k]. 2

Axel Thue

The ﬁrst systematic study of words or sequences of

numbers (“Zeichenreihen”) seems to have appeared in

three papers of Axel Thue

(1863-1922) in 1906, 1912,

and 1914 [184, 185, 186], and in a paper by MacMa-

hon in 1913 [137]. Thue’s work is on inﬁnite words

(sequences of symbols) and he investigated words from

a number-theoretic viewpoint. In the ﬁrst paper, he

asked the following question: Given any ﬁnite word

w = w

···w

on P = {p

,...,p

} and any inﬁnite

word w



on Q = {q

,...,q

}, is there a map Φ from

elements in P to ﬁnite words in Q, such that the word

Φ(w

) ···Φ(w

) has to occur in Q?

Thue showed that the answer is negative. In the subsequent papers [185, 186],

he investigated equivalence of sequences that are transformed by certain rules.

As an introduction to the 1912 paper, he wrote:

“F¨ur die Entwicklung der logischen Wissenschaften wird es, ohne

R¨ucksicht auf etwaige Anwendungen, von Bedeutung sein, aus-

gedehnte Felder f¨ur die Spekulation ¨uber schwierige Probleme zu

ﬁnden.” (It will be necessary for the development of the logical sci-

ences to ﬁnd vast areas for research on diﬃcult problems, without

regard to potential applications.)

By contrast, MacMahon approached words, which he called assemblage of

objects, in the context of partitions and permutations. His viewpoint and

questions are the ﬁrst instance of one of the main topics covered in this text,

namely enumerating statistics on words. We will state his deﬁnitions and

results in the modern terminology that will be used throughout the book,

http://www-history.mcs.st-andrews.ac.uk/Mathematicians/Thue.html

8 Combinatorics of Compositions and Words

but mention how he referred to those objects. Coming from the study of

permutations, MacMahon started with a list of parts, the assemblage,and

then considered any word that can be created from the parts in this set, that

is, all the permutations of the assemblage.

Deﬁnition 1.10 A permutation of [n]={1, 2,...,n} is a one-to-one func-

tion from [n] to itself. We denote permutations of [n] by π = π

···π

,and

the set of all permutations of [n] by S

(S stands for symmetric group).

The deﬁnition easily generalizes to any set of n elements, as any such set

can be associated with the set [n].

Example 1.11 There are six permutations of the assemblage 123,namely

123, 132, 213, 231, 312 and 321, and three permutations of the assemblage

112,namely112, 121,and211.

The statistics MacMahon investigated are based on the following relations

between consecutive letters in a sequence.

Deﬁnition 1.12 For any sequence s

···s

(permutation, word or composi-

tion),arise consists of a part followed by a larger part, a level or straight

occurs when a part is followed by itself, and a drop or fall consists of a part

followed by a smaller part. A rise, level, or drop occurs at position i if s

less than, equal to, or bigger than s

i+1

Note that MacMahon referred to a rise as a minor contact,alevelasan

equal contact,andadropasamajor contact.

Deﬁnition 1.13 For a given assemblage a

···a

(where a

indicates

that there are i

copies of the letter a

),letw be a permutation of these

letters. Then the greater index p of w is deﬁned to be the sum of the positions

i in w such that a drop occurs at position i. Likewise, the equal index q of w

is deﬁned to be the sum of the positions where a level occurs, and the lesser

index r is the sum of the positions where a rise occurs. If there are m rises

in w,thenw belongs to the class m with regard to rises. Likewise, we deﬁne

the class m with regard to levels and drops.

MacMahon then gave the generating function (see Deﬁnition 2.36) for the

greater index p. Using the symmetry of this function, he derived the following

interesting result.

Theorem 1.14 [138, item 106] The number of words associated with the as-

semblage

···a

with m rises is the same as the number of words with m rises associated with

any assemblage a



···a



,wherei



···i



is a permutation of i

···i

Introduction 9

Example 1.15 There are exactly six permutations that have a greater index

of p =3in each of the assemblages

3, 1

, 1

3, 1

, 12

For the assemblage 111223, the six words with a greater index of 3 are

112123, 122113, 321112, 113122, 123112, 223111;

for the assemblage 112333, the six words with a greater index of 3 are

113233, 321133, 123133, 133123, 233113, 333112.

From this result, he derived a second, related result.

Theorem 1.16 [138, item 107] Let p denote the greater index, and q denote

the lesser index. Then for any assemblage,



,wherethesumis

over all permutations of the given assemblage.

Proof We can map any word w of a given assemblage to a word w



mapping the largest part to the smallest part and vice versa, the second

largest part to the second smallest part, etc. Then each rise becomes a drop

and vice versa, so the lesser index of w matches the greater index of w



and

vice versa. Now we use Theorem 1.14 because the assemblage of w



is diﬀerent

from the assemblage of w (the powers have been mapped accordingly), and

the result follows. 2

MacMahon also investigated the special case of words with just two letters

with regard to the diﬀerence of the greater and the lesser index and derived

averages of the statistics of interest, a topic that we will discuss in Chapter 8.

Theorem 1.17 [138, item 109] For any word created from the assemblage

, the diﬀerence between the greater and the lesser index, p −r,equals−i

or j, depending on whether the word terminates with a 2 or a 1.

Proof The truth of the statement is easily checked for words of length one

or two. Assume the hypothesis is true for words associated with the assem-

blage 1

and let (1

)

and (1

)

indicate that the word ends in 1 or 2,

respectively. Then the hypothesis follows for words of length i + j +1 by

checking the four diﬀerent cases and computing the value of p − r in each

case:

)

1:p − r = j,

)

2:p − r = j − (i + j)=−i,

)

1:p − r = −i +(i + j)=j,

)

2:p − r = −i,

10 Combinatorics of Compositions and Words

so the result follows. 2

After these initial results on words, the literature became quiet for a while,

with the exception of a few individual papers. Schensted [177] in 1961 derived

results on the number of longest increasing and decreasing subsequences in

words, and Carlitz and his collaborators enumerated statistics on words as well

as the number of restricted words in a number of papers from the 1970s. In

1983, the ﬁrst of two volumes on the combinatorics of words from an algebraic

and group theoretic point of view appeared, authored by M. Lothaire, the

nom du plume for a group of authors that initially consisted of students of

M. P. Sch¨utzenberger. These volumes [130, 131] treat words from a diﬀerent

perspective, and the reader interested in algebraic and group theoretic results

is invited to study these texts and the references therein. In the algebraic

context, the term “avoidable word” often occurs, but this is diﬀerent from

the pattern avoidance considered here. Note that we will not give any further

references to this branch of study of words, except in cases where there is an

overlap.

Table 1.4 shows the time line for research on words in the early years,

while Table 1.5 shows the more recent developments. We once more have to

abbreviate an author’s name – Mac. refers to MacMahon in Table 1.4 and

Prod. refers to Prodinger in Table 1.5.

TABLE 1.4: Time line of research in major areas for words

Year Statistics Restricted Pattern Variations

arrangements avoidance

1906 Thue [184]

1912 Thue [185]

1913 Mac. [137]

1914 Thue [186]

1961 Schensted [177]

1972 Carlitz

†

[41] Carlitz [36]

1973 Carlitz [37]

1974 Carlitz

†

[43]

1976 Carlitz

†

[42]

1983 Lothaire[130]

Major activity in the statistics of words started at the end of the last decade

of the 20th century. Evdokimov and Nyu [62] derived results on the smallest

Introduction 11

length of a binary word w such that every word with exactly k ones and n −k

zeros can be obtained from w by deleting some letters. In 1997, incidentally

at the same time that the Combinatorics of Words [130] was reprinted, Foata,

who was one of the authors of that book, published two papers concerning

statistics on words. He and Han [70] showed that a certain transformation

gives an inverse for words which preserves the number of external inversions,

but not the number of internal inversions, and also showed existence of an

involution which preserves both types of inversions. The second paper by

the same authors [71] in 1998 established that certain transformations that

show the equality of some statistics can be obtained as special cases of a more

general procedure.

TABLE 1.5: Time line of research in major areas for words

Year Statistics Restricted Pattern Variations

arrangements avoidance

1992 Evdokimov

†

[62]

1997 Foata

†

[70]

1998 Burstein

†

[31] Foata

†

[71]

Regev [169] R´egnier

†

[170]

2001 Tracy [187]

2002 Lothaire [131]

2003 Burstein

†

[34] Burstein

†

[33] Burstein

†

[32]

Burstein

†

[35] Kitaev

†

[109]

2004 Dollhopf

†

[61]

2005 Br¨and´en

†

[27] Lothaire [132]

2006 Mansour [141]

2007 Bernini

†

[23]

2008 Kitaev

†

[110] Knop.

†

[116] Jel´ınek

†

[105] Mansour [142]

Prod. [166] Mansour [144] Firro

†

[65]

Myers

†

[158] Mansour [143]

In the same year, the study of subsequence patterns in words was initiated

by Regev [169], who found the asymptotic behavior for the number of k-ary

words avoiding an increasing subsequence of length . Subsequence patterns

were the ﬁrst type of patterns to be studied in permutations and subsequently

in words, by generalizing proof techniques developed for permutations. Tracy

and Widom [187] considered the asymptotic behavior of a related statistic,

12 Combinatorics of Compositions and Words

namely the length of the longest increasing subsequence, by considering ran-

dom words. However, the foundation of research on pattern avoidance in

words was laid in Burstein’s thesis [31], where he gave results for generating

functions for the number of k-ary words of length n that avoid a set of pat-

terns T ⊂S

. Various generalizations followed, to pattern avoidance in words

for multi-permutation subsequence patterns [33, 105] or pairs of more general

patterns of varying length. Mansour [141] considered the special case of words

that avoid both the pattern 132 and some arbitrary pattern, which leads to

generating functions that are expressed in terms of continued fractions and

Chebyshev polynomials of the second kind. Many of these papers generalize

methods used for permutations avoiding permutation patterns, but several

authors utilized diﬀerent methods, such as automata theory [27], the ECO

method [23], and the scanning-element algorithm [65]. Another variation was

considered by Dollhopf et al. [61], who enumerated words that avoid a set of

patterns of length two that describes a reﬂexive, acyclic relation.

Several authors considered other types of patterns besides subsequence pat-

terns and also studied enumeration instead of avoidance. Burstein and Man-

sour [34] considered the enumeration of words containing a subword pattern

of length  exactly r times, while Kitaev and Mansour [109] studied partially

ordered generalized patterns. Burstein and Mansour [35] also enumerated all

generalized patterns of length three. A somewhat related paper by Burstein

et al. [32] investigated the packing density for subword patterns, generalized

patterns and superpatterns.

The most recent papers investigated a wide range of topics. Kitaev et al.

[110] enumerate the number of rises, levels and falls in words that have a

prescribed ﬁrst element, while Prodinger [166] enumerated words according

to the number of records (= sum of the positions of the rises, or in the ter-

minology of MacMahon, the lesser index). Myers and Wilf [158] investigated

left-to-right maxima in words and multiset permutations. Knopfmacher et

al. [116] and Mansour [144] looked at smooth words and smooth partitions,

respectively, and obtained connections with Chebyshev polynomials of the

second kind. Finally, Mansour enumerated words [143] and words that avoid

certain patterns [142] according to the longest alternating subsequence.

Another variation is avoidance or occurrence of substrings in words. R´egnier

and Szpankowski [170] used a combinatorial approach to study the frequency

of occurrences of strings from a given set in a random word, when overlapping

copies of the strings are counted separately (see [170, Theorem 2.1]). Various

examples on enumeration of substrings in words are included in general texts

on combinatorics (see for example [75, 182]). This research area is also treated

in the third volume of the Lothaire series [132] which focuses on applied

combinatorics of words, for example genetics, where words are used to describe

DNA fragments (see Example 1.23). The reader who is interested in the

algorithmic aspects and the statistics connected to substrings in words will

ﬁnd this third volume a good starting point. We will restrict our focus to

patterns that encode relations as opposed to a speciﬁc string of letters.