Heubach S., Mansour T. Combinatorics of Compositions and Words

Подождите немного. Документ загружается.

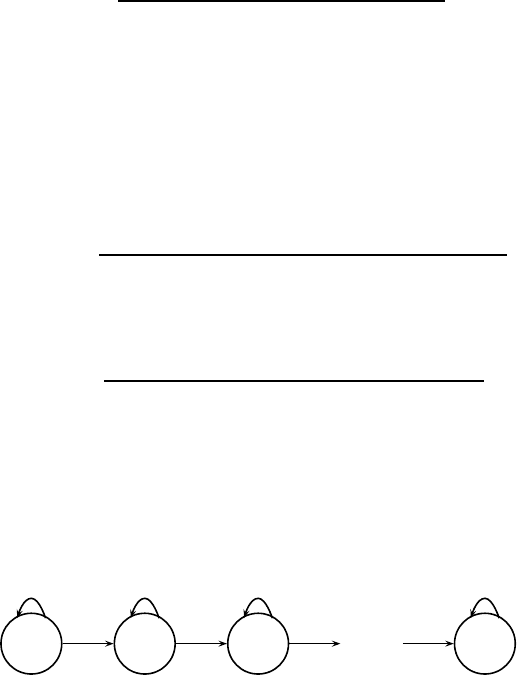
Automata and Generating Trees 285

Apply[Plus, Inverse[IdentityMatrix[3] - A][[1]]] // Factor

with the matrix A as deﬁned above, we obtain the generating function

123

[3]

(x)=

1 − x − x

+ x

(1 − x

− x

)(1 − x − x

)

This example can be generalized. The fact that the set A consists exactly

of the letters of the pattern forces a very speciﬁc structure on the automaton

which allows us to give an explicit formula for the generating function.

Theorem 7.71 Let τ = τ

···τ



be any subsequence pattern of length  with

d distinct letters. Then the generating function for the number of compositions

of n with m parts in [d] that avoid the pattern τ is given by

[d]

(x, y)=





j=1

(−1)

j−1

+···+τ

j−1

1 − y



i∈[d]\{τ

}

···

1 − y



i∈[d]\{τ

}

In particular,

[d]

(x)=





j=1

(−1)

j−1

+···+τ

j−1

1 −



i∈[d]\{τ

}

···

1 −



i∈[d]\{τ

}

Proof Let τ be any pattern of length  with d distinct letters. Then the

automaton that enumerates the number of compositions of n with parts in

A =[d] that avoid the pattern τ is given by Figure 7.15, where the state

t

 = τ

···τ

.

ε

t



···

t



−1

t

−1





i=τ



i=τ



i=τ



i=τ



FIGURE 7.15: Automaton for avoidance of τ ∈ [d]



Thus, the adjacency matrix is of the form

A =

⎡

⎢

⎣



i=τ

0 ··· 0



i=τ

··· 0

000

−1

000



i=τ



⎤

⎥

⎦

286 Combinatorics of Compositions and Words

We now use Equation (7.1) of Theorem 7.33 and compute (I − yA)

−1

.Note

that for compositions, the length of the walk is enumerated by y,thenumber

of parts of the composition. Now let B be an × matrix of the form B =(B

)

with B

= α

, B

i,i+1

= β

,andB

=0forallj − i =0, 1. Then it can be

shown by induction that B

−1

=(B

−1

)

is given by

−1

)

⎧

⎨

⎩

0, if i>j

(−1)

i+j

i+1

···β

j−1

i+1

···α

if i ≤ j

Thus for B = I −yA we have that

=1− y



i=τ

and β

= yx

This implies that the ﬁrst row of B

−1

is given by

⎡

⎣

1 − y



i=τ

−yx



j=1

1 − y



i=τ

, ··· ,

(−1)

−1



−1

j=1





j=1

1 − y



i=τ

⎤

⎦

Adding these entries yields the desired result. 2

We can obtain a similar result for avoidance of subword patterns in com-

positions.

Theorem 7.72 Let τ = τ

···τ



be any subword pattern of length  with d

distinct letters. Then the generating function for the number of compositions

of n with m parts in [d] that avoid the pattern τ is given by

[d]

(x, y)=



−1

j=1

+···+τ

1 −





j=1

+···+τ

j−1



i∈[d]\{τ

}

In particular,

[d]

(x)=



−1

j=1

+···+τ

1 −





j=1

+···+τ

j−1



i∈[d]\{τ

}

Proof See Exercise 7.8. 2

We conclude this section with an example for the generalized pattern 12–3.

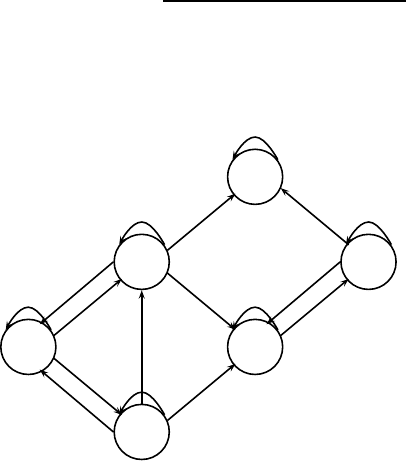
Example 7.73 Figure 7.16 shows the automaton for compositions in A =[4]

that avoid the pattern 12–3. Using the order of states

ε, 1, 2, 12, 13, 131,

Automata and Generating Trees 287

the adjacency matrix for this automaton is given by

⎡

⎢

⎣

+ x

000

0 x

000x

+ x

0000x

+ x

000x

⎤

⎥

⎦

To see that Δ(131) = 131, note that 13123

 1323. Using Maple or Math-

ematica as in Example 7.70, we can obtain the generating function AC

12−3

[4]

(x)

12−3

[4]

(x)=

(1 − x)

(1 − 4x +3x

− x

)(1 − 2x)

ε

1

2

12

13

131

+ x

FIGURE 7.16: Automaton for compositions in [4] avoiding 12–3.

Note that for generalized patterns the automaton can have cycles, unlike

in the case of subsequence patterns, where a cycle would have resulted in all

equivalence classes in the cycle being in the same class. Here, however, the

adjacency requirements prevent that the equivalence classes of a cycle are the

same.

Finally a word on automata for avoiding substrings. We have not focused

on these types of patterns but want to point out that automata are very well-

suited for enumeration of words or compositions avoiding substrings. The

288 Combinatorics of Compositions and Words

main reason is that for a substring, we only have to consider the last letter,

not a history.

Example 7.74 We look at the automaton for avoidance of the substring 123

in words on the alphabet [4]. For avoidance of substrings, the states are of the

form s

···s

 for j =1, 2,...,− 1 for a substring pattern s

···s



.So

for the pattern 123 we have states ε, 1,and12. The transfer matrix is

given by

A =

⎡

⎣

310

211

210

⎤

⎦

Using Mathematica or Maple we can obtain the generating function as

123

[4]

(x)=

1 − 4x + x

and the number of words on [4] avoiding the substring 123 for n =0, 1,...,15

is given by 1, 4, 16, 63, 248, 976, 3841, 15116, 59488, 234111, 921328,

3625824, 14269185, 56155412, 220995824,and869714111.

7.4 Generating trees

Generating trees were introduced by West in [191] as a method to capture

the structure of a recurrence. He coined the term transfer matrix for the

adjacency matrix of the digraph associated with the generating tree. Since

this has become standard terminology in any paper on generating trees, we

will use the term transfer matrix instead of adjacency matrix. We will also

see that we can translate any generating tree into an associated automaton.

Deﬁnition 7.75 A generating tree is a rooted labeled tree such that if v

and

are two nodes with the same label, and  is any label, then v

and v

have

exactly the same number of children with label . To specify a generating tree

it therefore suﬃces to specify:

1. the label of the root, and

2. a set of succession rules explaining how to derive from the label of a

parent the labels of all of its children.

Example 7.76 (The complete binary tree) The complete binary tree is a tree

in which each vertex has exactly two children. Since all the nodes in the

complete binary tree are identical, it is enough to use only one label, which we

choose to be (2). So we get the following description:

Automata and Generating Trees 289

Root:(2)

Rule:(2) (2)(2).

Example 7.77 (The Fibonacci tree) The Fibonacci tree has many uses in

computer science applications. It is a variant of the binary tree and can

be visualized as follows. The root is a red vertex. A red vertex has a blue

oﬀspring, and a blue vertex has a blue and a red oﬀspring. The two diﬀerent

types of vertices are thus distinguished by the number of oﬀspring, so we label

the vertices according to their number of children and obtain these rules:

Root:(1)

Rules:(1) (2), (2)  (1)(2)

We can encode the information from the generating tree as an automaton

whose states correspond to the labels. Furthermore, we place an edge from

vertex l

to vertex l

for every occurrence of l

in the succession rule of l

given

by (l

) →···. We use the integers from 1 to the maximum number of labels

in all the succession rules as the “alphabet” for the edge labels. Formally, we

have the following deﬁnition of the automaton.

Deﬁnition 7.78 For the automaton of a generating tree, the set of states E

consists of the labels of the generating tree. The alphabet is Σ={1, 2,...,m},

where m is the maximal number of labels in any of the succession rules. For

any label l

with succession rule (l

)  (l

)(l

) ···(l

), the transition rule is

deﬁned by Δ((l

),k)=(l

) for k =1,...,j. S

is the label of the root, and

F = E.

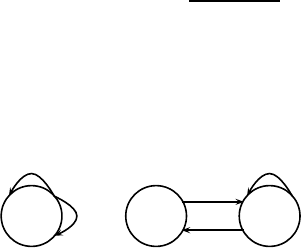
Example 7.79 (Continuation of Example 7.76) The automaton for the com-

plete binary tree is given by

E = {(2)}, Σ={ 1, 2}, Δ((2), 1) = Δ((2), 2) = (2),S

=(2),

and its graph is shown in Figure 7.17. The transfer matrix for the binary tree

is A =[2].Using(7.1) of Theorem 7.33 we obtain that the generating function

for the number of vertices at height n (which correspond to paths of length n

starting from the root) in the complete binary tree as

1−2x



n≥0

,and

we recover the well-known result that the number of vertices at height n in the

complete binary tree is given by 2

. This is a rather trivial application of the

transfer matrix, but it shows the power of the approach.

Example 7.80 (Continuation of Example 7.77) The automaton for the Fi-

bonacci tree is given by

E = {(1), (2)}, Σ={1, 2}, Δ((1), 1) = (2), Δ((2), 1) = (1), Δ((2), 2) = (2),

290 Combinatorics of Compositions and Words

with initial state S

=(1). The corresponding transfer matrix is

A =

To compute the generating function for the number of vertices at height n,we

need to compute the sum of the entries in the ﬁrst row of

(I − xA)

−1

1 −x

−x (1 − x)

−1

1 − x − x

1 − xx

x 1

and we obtain the generating function as 1/(1−x−x

). This is the generating

function of the sequence {f

}

,wheref

is the n-th shifted Fibonacci number

(see Table A.1).

(2)

1 (1) (2)

FIGURE 7.17: Automata for the complete binary and Fibonacci trees.

Generating trees were used by West in [191] to enumerate permutations

avoiding a given subsequence pattern τ ∈S

. We start by giving the gener-

ating tree for the set of permutations S

Example 7.81 The permutations in S

n+1

can be created from the permuta-

tions in S

by inserting the value n+1 at all possible positions in the permuta-

tions of n. Since each permutation in S

creates exactly n+1 permutations of

size n+1, the labels chosen for the generating tree give the number of children,

with the empty permutation denoted by ε and given the label (1). Therefore,

the succession rules are

Root:(1)

Rules:(n)  (n +1)

where (i)

is shorthand for k labels (i). The generating tree for the per-

mutations is given in Figure 7.18, showing both the permutations and their

respective labels.

The next step is to derive generating trees for permutations that avoid a

pattern τ.

Example 7.82 Given a pattern τ, one can deﬁne the rooted tree for permu-

tations avoiding τ as follows. The nodes at level n are precisely the elements

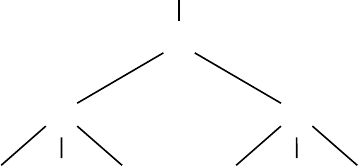
Automata and Generating Trees 291

(1)

(2)

(3)

(4)

312

(4)

132

(4)

123

(3)

(4)

321

(4)

231

(4)

213

FIGURE 7.18: Generating tree for S

of S

(τ). The parent of a permutation π = π

···π

n+1

∈S

n+1

(τ) is the

unique permutation π



= π

···π

j−1

j+1

···π

such that π

= n+1. Note that

here we deﬁne the parent via the child, which ensures that the τ-avoidance is

preserved. If we were to deﬁne the child via the parent, then we would have

to delete those children for which the insertion of the value n creates an oc-

currence of the pattern τ.

Deﬁnition 7.83 The generating tree whose vertices at level n are the permu-

tations of S

(τ) is denoted by T (τ). Similarly, the tree corresponding to the

set S

(T ) is denoted by T (T ).

The diﬃcult work, which is truly an art, consists of translating this back-

ward structural description of the generating tree T (T ) into succession rules.

The “translation” is known for some patterns, and not for others. We will

give the rules for the generating trees T (123) and T ({123, (k − 1) ···1k}).

More examples of pattern avoidance in permutations can be found in [25] and

the references cited therein.

Example 7.84 West derived the generating tree T (123) [192, Example 4].

In this case the pattern to be avoided creates a very distinctive structure. If

the permutation of n has at least one rise, with the leftmost rise π

position i

, then we can insert the part (n +1) only at positions 1, 2,...,i

where insertion at position i means the placement of the new part between

i−1

and π

. If insertion is at position 1,theleftmostrisenowoccursat

position i

+1; otherwise, the leftmost rise occurs at the insertion position i.

If a permutation of n does not have any rise, then we can insert (n+1) at any

of n +1 positions, creating a rise at position i if the insertion is at position

i>1. Insertion at position 1 does not create a rise, which we can express

as a rise at n +2 in order to combine the two cases. Overall, we have these

292 Combinatorics of Compositions and Words

rules, where the label indicate the position of the rise and the number of the

children (why?):

Root:(1)

Rules:(p)  (p + 1)(2)(3) ···(p).

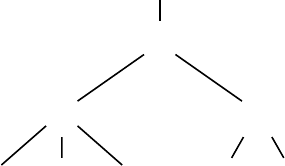
Figure 7.19 gives the generating tree T (123) showing both the permutations

and the respective labels.

(1)

(2)

(3)

(4)

321

(2)

231

(3)

213

(2)

(3)

312

(2)

132

FIGURE 7.19: Generating tree for 123-avoiding permutations.

Example 7.85 Chow and West [53] proved that the succession rules for the

tree T ({123, (k − 1) ···1k}) are

Root:(2)

Rules:(l)  (2) ···(l)(l +1),l<k− 1

(k − 1)  (2) ···(k − 2)(k − 1)(k − 1).

Note that in this case, the label indicates the number of children of the vertex.

The corresponding graph is shown in Figure 7.20. The transfer matrix is given

⎡

⎢

⎣

1100··· 000

1110··· 000

1111··· 000

1111··· 100

1111··· 110

1111··· 111

1111··· 112

⎤

⎥

⎦

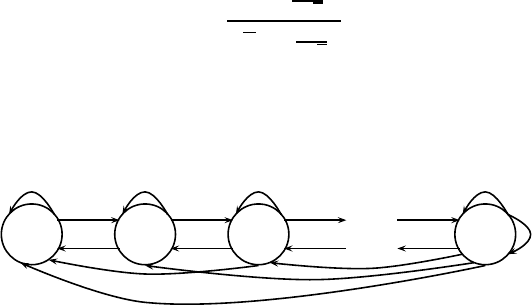
Automata and Generating Trees 293

It is well known (see [53, Thereom 3.1] ) that the generating function for the

number of permutations in S({123, (k − 1) ···21k)}) is given by

k−1

√

where U

are the Chebyshev polynomials of the second kind (see Appendix

C.2).

(2)

(3)

···

(4)

k-1

k-2

(k-1)

2 3 4 k − 1

k − 1

FIGURE 7.20: The automaton for T (123, (k − 1) ···21k).

We will now look at generating trees for words.

Example 7.86 Every k-ary word of length n +1 can be created from a k-ary

word of length n by adding one of the letters in [k]. Thus, we get a k-ary

tree, that is, a tree where each vertex has exactly k children, and therefore, all

vertices have the same label. If we let the label denote the number of children,

then the succession rules are as follows:

Root:(k)

Rules:(k)  (k)

The generating tree for 2-ary words is shown in Figure 7.21.

Example 7.87 The set C

of compositions of n has almost the same succes-

sion rules as the binary tree, as each composition of n creates two compositions

of n +1 by either appending a 1 on the right side or by increasing the right-

most part by 1. The only diﬀerence is the root, which corresponds to the empty

composition. It has only one child, the composition 1. Therefore, the rules

are:

Root:(1)

Rules:(1) (2)

(2)  (2)

294 Combinatorics of Compositions and Words

(2)

FIGURE 7.21: Generating tree for 2-ary words.

We now discuss the ECO method, a general framework for enumeration of

combinatorial objects that is closely related to generating trees and therefore

to automata.

7.5 The ECO method

We start by presenting the general framework for the ECO method. In

essence, it is a road map (much like the Noonan-Zeilberger algorithm) in that

it lays out the task to be done, but does not give a formulaic description of

the steps.

Deﬁnition 7.88 Let O be a class of objects which have an associated concept

of size, that is, there exists a map p : O→N, such that

| = |{O ∈O|p(O)=n}|

is ﬁnite. An operator ϑ on the class O maps O

to 2

n+1

,where2

n+1

is the

power set of O

n+1

Now we can present the main result for the ECO method, which asserts

that there is a recurrence which allows the construction of all elements of size

n + 1 from those of size n.

Theorem 7.89 [16, Proposition 2.1] Let ϑ be an operator on O.Ifϑ satisﬁes

the following conditions:

1. For each O



∈O

n+1

,thereexistsO ∈O

such that O



∈ ϑ(O).

2. If O, O



∈O

such that O = O



,thenϑ(O) ∩ ϑ(O



)=∅.

Then the family of sets {ϑ(O):O ∈O

} is a partition of O

n+1