Heubach S., Mansour T. Combinatorics of Compositions and Words

Подождите немного. Документ загружается.

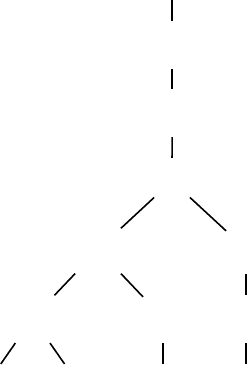
Automata and Generating Trees 305

Proof We can generate the (1,k)-compositions of n + 1 by either appending

a1toacompositionofn,orconvertingthek − 1 rightmost consecutive 1s

into a k. A composition with at least k −1 consecutive rightmost 1s therefore

produces two new compositions (label (2)), while all other compositions pro-

duce one new composition. We use the label (1

) to denote a composition that

has i consecutive rightmost 1s. The root is the empty composition, with label

). Note that the algorithm does not produce duplicates, and creates all

(1,k)-composition of n + 1 from those of n. Figure 7.24 shows the generating

tree for (1, 4)-compositions. 2

)

(2)

111

(2)

1111

(2)

11111

(2)

111111

)

114

)

141

)

411

FIGURE 7.24: Generating tree for (1, 4) compositions.

We give one more example of the compositions listed in [17, Table 1], namely

the succession rules for the compositions with largest part p.

Example 7.96 The succession rules for compositions in [k] with largest part

p where k ≥ p are given by

306 Combinatorics of Compositions and Words

Root:(0)

Rules:(0) (1)

(i)  (1)(i +1), for 1 ≤ i ≤ p − 1

(p)  (1)

The derivation of these rules is left as Exercise 7.11.

7.6 Exercises

Exercise 7.1 The adjacency matrix for the automaton for avoidance of the

subsequence pattern 3241 is given in Example 7.32. Carefully explain the

following edges: 42→324, 432→3243,and3243→435.

Exercise 7.2 Determine the adjacency matrices for the automata A(τ, 4)

where τ is a permutation pattern in S

. Several of the patterns in S

have

isomorphic graphs, so their adjacency matrices will be identical for an appro-

priate ordering of states.

(1) Determine the number of nonisomorphic graphs. Justify your answer by

stating the canonical ordering of states that show that certain graphs are

isomorphic, and giving a reason why the other graphs are nonisomorphic.

(2) All permutation patterns of length three are in the same Wilf-equivalence

class and thus have the same generating function. Show that each of the

nonisomorphic adjacency matrices leads to the same generating function

using the formula given in Theorem 7.34.

Exercise 7.3 Let τ =11–2 be a generalized pattern of type (2, 1).Findthe

automata A(τ,k) for the number of k-ary words that avoid τ for k =2and

k =3.

Exercise 7.4 Prove that the automaton given in Figure 7.25 counts the num-

ber of smooth k-ary words of length n (see Exercises 2.17 and 6.9 ).

Exercise 7.5 Find the simple paths associated with each of the Young

tableaux of Figure 7.13 (see Example 7.53 ).

Exercise 7.6 Fill in the details of the proof of Corollary 7.65.

Exercise 7.7 Use the algorithm given in Lemma 7.40 to derive the automa-

ton A(1234, 5).

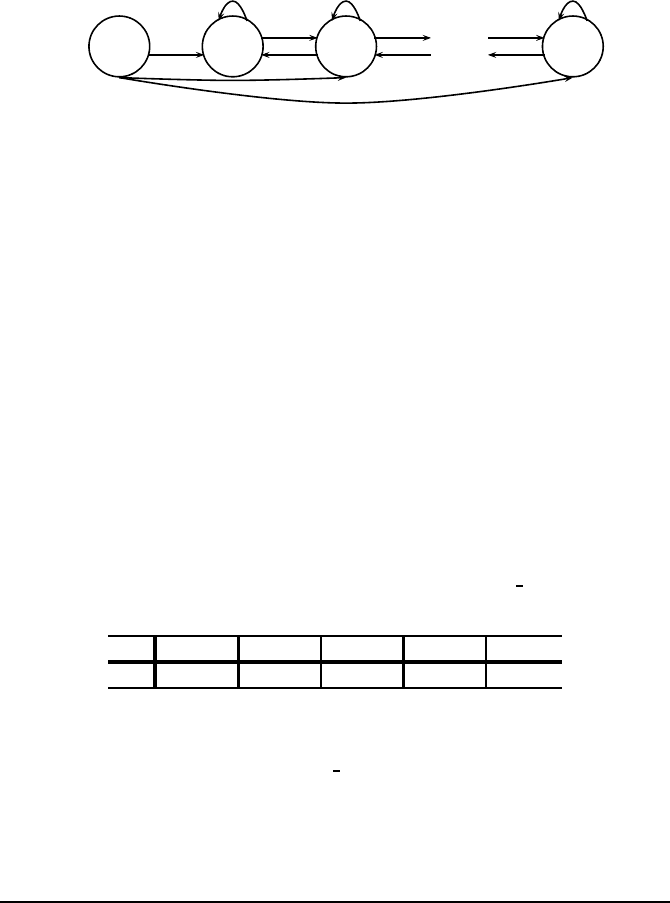
Automata and Generating Trees 307

ε 1 1

···

2

k − 1

k

1 2 k

FIGURE 7.25: Automaton of smooth words.

Exercise 7.8 Give the proof of Theorem 7.72.

Exercise 7.9 Let τ =11–2 be a generalized pattern of type (2, 1).Findthe

automata A(τ,k) for the number of compositions of n with parts in [k] that

avoid τ for k =2and k =3.

Exercise 7.10 Derive the generating function for the number of compositions

avoiding the set of patterns {123, 132, 122} using any method discussed so far.

Exercise 7.11 Derive the succession rules given in Example 7.96 for the re-

cursive creation of the compositions in [k] with largest part p.

Exercise 7.12 Let N(τ, k) be the number of accept states in the automaton

A(τ,k) for pattern avoidance in words, that is, N (τ, k)=|E(τ,k)|−1.From

Lemma 7.40 we obtain that N(1234,k)=





. For the pattern 1324,weobtain

the ﬁrst few values of N(1324,k) by using the program TOU

AUTO (available

on Mansour’s home page [139] ) as given in the table below.

τ N (τ, 4) N (τ,5) N(τ, 6) N (τ,7) N (τ,8)

1324 4 12 34 98 294

The values of N (τ, k) for the pattern τ = 1324 coincide with the values of

the sequence A014143 in the Online Encyclopedia of Integer Sequences [180]

(with a shift).UsetheprogramTOU

AUTO to determine the next two (or

possibly three) values in the sequence N(1324,k) and check whether they still

agree with the values of the sequence A014143.

7.7 Research directions and open problems

We now suggest several research directions, which are motivated both by

the results and exercises of this chapter. In later chapters we will revisit some

of these research directions and pose additional questions.

308 Combinatorics of Compositions and Words

Research Direction 7.1 Table 6.3 shows that there are ﬁve Wilf-equivalence

classes for permutation patterns of length four, namely 1234 ∼ 1243 ∼ 1432 ∼

2143, 1324, 1342, 1423 and 2413. Theorem 7.54 gives the asymptotic expres-

sion for the number of words avoiding 1234 for all k ≥ 3 as

1234

[k]

(n) ≈

2 · (3(k − 3)!)

(k − 3)!(k − 2)!(k − 1)!

(k−3)

n−3k+9

(n →∞).

A natural extension is to ask about ﬁnding the asymptotics for the number of

k-ary words of length n that avoid a subsequence pattern τ from the remaining

four Wilf-equivalence classes, namely for τ = 1324, τ = 1342, τ = 1423 and

τ = 2413.

Research Direction 7.2 We were able to obtain results for the increasing

patterns since the automaton for those patterns had a very speciﬁc structure

for the loops. This leads to the following questions:

(1) Are there subsequence permutation patterns τ that have an automaton

A(τ,k) where each state has exactly  − 1 loops for all k>k

,where

is the number of letters in τ and k

is ﬁxed (to avoid the special cases

when k is too small)?

(2) More generally, are there subsequence permutation patterns τ that have

an automaton A(τ,k) such that the set of the number of loops in the

automaton is L for all k>k

, for a given set L and ﬁxed k

?For

example, if L = {3}, τ = 1234 would be such a pattern. If L = {2, 3},

then from Example 7.32, the pattern 3241 could be a candidate (as we

do not know that the loop pattern is the same for all k).

Research Direction 7.3 In Lemma 7.40 we showed that the number of ac-

cept states for the automaton A(τ



,k) is given by N (τ



,k)=







.Belowisa

table of the ﬁrst few values of N(τ,k) for permutation patterns of length four

from each of the ﬁve Wilf-equivalence classes (see Table G.3), as computed

using the program TOU

AUTO (except for τ = 1234).

τ N (τ,4) N (τ,5) N(τ,6) N (τ,7) N (τ,8)

1234 4 10 20 35 56

1324 4 12 34 98 294

1342 4 14 48 164 560

1423 4 14 45 136 396

2413 4 18 72 280 1072

The following questions arise:

(1) Compute the ﬁrst few values of N(τ,k) for the remaining patterns of

length four, both permutation patterns and patterns with repeated let-

ters. Remember that even though τ and ρ may belong to the same Wilf-

equivalence class, N(τ,k) and N (ρ, k) may be diﬀerent (see Exercise

Automata and Generating Trees 309

7.2). The only general rule we have is that N(τ,k)=N(c(τ),k),thus

reducing the number of patterns to be considered by a factor of one half.

(2) In Exercise 7.12 we saw that the values of N (1324,k) for k ≥ 3 co-

incide with the values of the sequence A014143, which enumerates the

partial sums of the Catalan numbers. Give a combinatorial proof that

N(1324,k)=



k−3

i=0

,whereC

is the i-th Catalan number.

(3) Find an explicit formula for N(τ,k),whereτ is any of the other subse-

quence pattern of length four.

(4) Compute values and ﬁnd an explicit formula for N(τ,k),whereτ is a

subsequence pattern of length ﬁve.

Research Direction 7.4 We have derived formulas for pr(, i, r),thenum-

ber of primitive segmented tableaux in [] ×[i] with r diﬀerent entries, for two

special cases, namely i = r (see Theorem 7.57) and  =2(see Theorem 7.58).

Br¨and´en and Mansour [27] derived a system of equations for the generating

function of pr(, i, r), but did not succeed in solving it. Either ﬁnd a clever

way of solving this system of equations, or ﬁnd a diﬀerent approach to derive

explicit formulas for pr(, i, r) or the corresponding generating functions. Of

speciﬁc interest is pr(3,i,r), which would lead to a formula for the number of

k-ary words avoiding the subsequence pattern 1234.

Research Direction 7.5 A noncrossing (nonnesting) word w is a word that

avoids the subsequence pattern 1212 (1221). Find explicit formulas for the

number of k-ary noncrossing (nonnesting) words of length n. (Note that the

terminology comes from noncrossing and nonnesting partitions and matchings.

For details see [47, 112, 113] ).

Chapter 8

Asymptotics for Compositions

8.1 History

Asymptotic analysis usually involves complex analysis or probability the-

ory or both. The idea is to get a handle on the behavior of the number of

compositions or words of interest, or of a statistic on these objects as n →∞.

Applying results from complex analysis we can obtain growth rates for the

statistics of interest. On the other hand, when considering compositions as

randomly selected from all compositions (that is, all compositions of n are

equally likely to occur), we can derive results on the average or variance of a

statistic, which now is a random variable.

Bender [18] blended the two approaches and gave results on the asymptotic

distribution for the quantity of interest based on a generating function that

keeps track of the order of the composition and one other statistic, such as

the number of parts. Later on, Bender and Richmond derived central and

local limit theorems for multi-variate generating functions [21].

Major research activity in the area of asymptotics for compositions started

with a paper by Hwang and Yeh [102] who looked at measures of distinct-

ness in random partitions and compositions, where distinctness is deﬁned as

the number of distinct part sizes in the composition (or partition). Their

results on the average number of distinct parts revealed an expression that

grows at a rate that is essentially log n (where log without base refers to the

natural logarithm), based on a mixture of complex analysis and probability

theory. Hitczenko and Stengle [97] proved the asymptotic result on the av-

erage number of distinct parts given by Hwang and Yeh in a diﬀerent way.

(The approach of Hwang and Yeh was more general and thus required more

machinery. Apparently, Hitczenko and Stengle were unaware of the results of

Hwang and Yeh.) We will present the shorter proof of Hitczenko and Stengle

as well as variations on the theme by Hitczenko and several collaborators.

With Louchard [93], Hitczenko derived more detailed results on the distri-

bution of the number of distinct part sizes and also considered the statistics

largest part and ﬁrst empty part (ﬁrst part size that is missing in the com-

position). Hitczenko and Savage [95] reﬁned these results by deriving results

on the multiplicity of parts in a random composition. Finally, Louchard [133]

provided further analysis on the multiplicity of parts, studying for example

311

312 Combinatorics of Compositions and Words

the maximum part size of multiplicity m.

Similar questions were studied for Carlitz compositions. Knopfmacher and

Prodinger [119] studied asymptotics for the number of parts, occurrences of

the (subword) pattern 11 (with Carlitz compositions being those that have a

zero count of the pattern 11), largest part, and other restricted compositions.

Their results were based solely on complex analysis tools. Louchard and

Prodinger added tools from probability and derived results on the number of

parts, the last part size, and correlation between successive parts in Carlitz

compositions. They made use of the results of Bender [18] repeatedly to obtain

asymptotic distribution results. Finally, Goh and Hitczenko [73] obtained

results on the average number of distinct part sizes in Carlitz compositions.

Most recently, Mansour and Sirhan [145] have obtained generating functions

and asymptotics for the number of compositions that avoid subword patterns

of length three and longer using tools from complex analysis as well as central

and local limit theorems based on Bender’s results [18].

We present a sampling of these results in the following sections. In Sec-

tion 8.2 we give the necessary background from probability theory and derive

explicit results for some average statistics. Section 8.3 contains the necessary

background from complex analysis. In the next two sections we give a sample

of asymptotic results for compositions and Carlitz compositions and provide

outlines of the proofs of these results. Note that there are very few asymp-

totic results for words. This is simply because the generating function for

the number of words avoiding a pattern is rational, and therefore asymptotic

results are easy to come by. We will present an example in Section 8.6.

As before, our focus is on compositions and words. However, the interested

reader who wants to delve deeper into asymptotics for more general combi-

natorial enumeration is referred to the recent book of Flajolet and Sedgewick

[68]. This book contains literally hundreds of examples and is a one-stop ref-

erence for techniques for asymptotic analysis.

8.2 Tools from probability theory

Oftentimes we are interested in the value of a statistic for a “typical” com-

position. We can compute this “typical” value by assuming that we are pre-

sented with a composition that is randomly selected from all compositions of

n, making all compositions of n equally likely. Then the statistic becomes a

random quantity and we can compute its average and its variance. If we know

an explicit formula for the number of compositions for which the statistic has

a given value, then we can compute the average of the statistic over all com-

positions, or equivalently, the “typical” value of the statistic for a randomly

Asymptotics for Compositions 313

selected composition.

To describe this approach, we only need very basic deﬁnitions from prob-

ability theory. We restrict ourselves throughout to deﬁnitions for countable

sample spaces, as those are the only ones to be considered here. The deﬁni-

tions and result we give, as well as the corresponding deﬁnitions and results

for more general sample spaces, can be found for example in [24, 80].

Deﬁnition 8.1 The sample space Ω is the set of all possible outcomes of

an experiment. A subset E of Ω is called an event.Anevent occurs if any

outcome ω ∈ E occurs. The probability function P :Ω → [0, 1] satisﬁes the

following three axioms:

1. For any E ⊆ Ω, P(E) ≥ 0.

2. P(Ω) = 1.

3. For a countable sequence E

,... of pairwise disjoint sets (that is,

= E

for i = j), P(E

∪ E

∪···)=



P(E

The value P(E) gives the probability that the event E will occur.

As a consequence of the third axiom it is enough to specify P({ω})foreach

of the outcomes ω ∈ Ω when Ω is a countable set.

Deﬁnition 8.2 If all outcomes in a (ﬁnite) sample space are equally likely,

then we say that the sample space is equipped with the uniform probability

measure. In this case, P({ω})=1/|Ω| for every ω ∈ Ω. Consequently for any

subset E of Ω,

P(E)=

|E|

|Ω|

We will consider what happens to a statistic of a random composition with

certain characteristics, for example, the number of parts (statistic) in Carlitz

compositions (compositions with certain characteristics) of n when n is large.

Thus our sample space is the set of all compositions with those characteristics,

for example compositions with parts in N, Carlitz compositions, and so on.

Unless stated otherwise, we will assume that the sample space is equipped

with the uniform probability measure.

Deﬁnition 8.3 A discrete random variable X is a function from Ω to a

countable subset of R.Itsprobability mass function is deﬁned by

P(X = m)=P({ω | X(ω)=m}).

The set of values together with their respective probabilities characterize the

distribution of X. If the set of values of X is given by {x

,...}, then the

probability mass function satisﬁes the following properties:

314 Combinatorics of Compositions and Words

1. P(X = x)=0if x ∈{x

,...}.

2. P(X = x

) ≥ 0 for i =1, 2,...



∞

i=1

P(X = x

)=1.

Note that it is customary to denote the random variable with a capital

letter and its values with the corresponding lower case letter.

Example 8.4 Let Ω=C

be the set of compositions of 5, where we assume

that all compositions occur equally likely. Then X =par(σ) for σ ∈C

a discrete random variable that takes values m =1, 2, 3, 4, 5.Therespective

(nonzero) probabilities are computed via the compositions (outcomes) that have

m parts.

12 3 4 5

ω 5 14 113 1112 11111

41 131 1121

23 311 1211

32 122 2111

212

221

P(X = m)

In this particular case, we could have computed the probabilities by using The-

orem 1.3, as it gives the number of compositions of n with exactly m parts



n−1

m−1



. For larger values of n and if we have no explicit formulas for

the quantity of interest, we can use Mathematica or Maple to compute the

probabilities. For example, in Mathematica, we can use the following code to

compute the probability distribution for X =par(σ) and obtain the values for

n =5:

comps[n_]:=Flatten[Map[Permutations,IntegerPartitions[n]],1]

probs[n_]:=BinCounts[Map[Length,comps[n],1],{Range[1,n+1]}]

/Length[comps[n]]

probs[5]

which gives the result





Other random variables on this sample space are X = number of occur-

rences of a pattern τ or X= largest part in the composition (see Exercise 8.1).

Example 8.4 is an illustration of the following lemma.

Lemma 8.5 Let Ω be ﬁnite, and |Ω| = N .IfΩ is equipped with the uniform

probability measure and X is a discrete random variable on Ω,then

P(X = m)=|{ω | X(ω)=m}|/|Ω|.

Asymptotics for Compositions 315

Deﬁnition 8.6 For a discrete random variable X which takes values i ∈ Z

with probability P(X = i), the expected value of f(X) for a (measurable)

function f is deﬁned as

E(f(X)) =



i∈Z

P(X = i)f (i),

assuming that the sum converges. In particular, the mean (or average or

expected value) μ and the variance Var(X) of X are given by

μ = E(X)=



i∈Z

iP(X = i)

and

Var(X)=σ

= E



(X −μ)



= E(X

) − μ

The quantity E(X

) is called the k-th moment of X,andσ =

Var(X) is

called the standard deviation of X.Furthermore,

E(X(X − 1)(X − 2) ···(X −k +1))

is called the k-th factorial moment of X.

Example 8.7 (Continuation of Example 8.4) Using the distribution derived

in Example 8.4 for the random variable X =par(σ), we have that

E(X)=

and

Var(X)=





− 3

=1.

We can easily derive a general formula for the mean and the variance of a

statistic if all compositions under consideration are equally likely.

Lemma 8.8 If Ω is equipped with the uniform probability measure, |Ω| = N

and a

n,m

is the number of compositions of n with a given characteristic such

that the statistic X has the value m,then

E(X)=E(X(n)) =



n,m

· m. (8.1)

Proof Follows immediately from the deﬁnition of the expected value and

Lemma 8.5. 2

Using Equation (8.1) it is straightforward to compute the average value of a

statistic X if we have an explicit formula for the quantity a

n,m

. To illustrate

this, we will compute the average number of parts in all compositions of n

and in all palindromic compositions of n.