Heubach S., Mansour T. Combinatorics of Compositions and Words
Подождите немного. Документ загружается.

326 Combinatorics of Compositions and Words
Clearly, C
A
(z) is meromorphic having two poles
ρ
1
=(−1+
√
5)/2=0.618034 = −β
and
ρ
2
=(−1 −
√
5)/2=−1.61803 = −α.
Thepoleofsmallermodulusisρ
∗
=(−1+
√
5)/2.Sinceh(z)=1− z − z
2
,
we obtain that
−1
ρ
∗
· h
(z)
(
(
(
(
z=ρ
∗
=
1
ρ
∗
(1 + 2ρ
∗
)
=0.723607.
Therefore,
C
A
(n) ≈ 0.723607(1.61803)
n
.
Note that we give between six and ten significant digits in numerical ap-
proximations. So, for example, ρ
1
=(−1+
√
5)/2=0.618034 should be
interpreted as ρ
1
=0.618034 ···.
A final result that is of great importance for establishing that a numerically
computed root is indeed associated with the dominant singularity is Henrici’s
Principle of the Argument, which we will use in several instances.
Theorem 8.27 (Henrici’s Principle of the Argument) [83, Theorem 4.10a]
Let f(z) be analytic in a region and let γ be a simple closed curve in the
interior of ,wheref (z) =0on γ. Then the number of zeros of f (z)(counted
with multiplicities) inside γ equals the winding number of the transformed
contour f(γ) around the origin.
Surprisingly, complex analysis also helps us establish asymptotic results
in terms of convergence to a normal distribution (see Definition 8.19). The
following proposition is a corollary to a more general result by Bender [18,
Theorem 1].
Proposition 8.28 [18, Section 3] Suppose that
f(z,w)=
n,k≥0
a
n
(k)z
n
w
k
=
g(z,w)
P (z,w)
,
where
(i) P (z, w) is a polynomial in z with coefficients continuous in w,
(ii) P (z, 1) has a simple root at ρ
∗
and all other roots have larger absolute
value,
(iii) g(z,w) is analytic for w near 1 and z<ρ
∗
+ ε,and
© 2010 by Taylor and Francis Group, LLC

Asymptotics for Compositions 327
(iv) g(ρ
∗
, 1) =0.
Then
μ = −
r(z, w)
ρ
∗
(
(
z=ρ
∗
,w=1
and σ
2
= μ
2
−
s(z,w)
ρ
∗
(
(
z=ρ
∗
,w=1
,
where
r = r(z, w)=−
∂
∂w
P
∂
∂z
P
(8.9)
and
s = s(z,w)=−
r
2
∂
2
∂z
2
P +2r
∂
∂z
∂
∂w
P +
∂
∂w
P +
∂
2
∂w
2
P
∂
∂z
P
. (8.10)
If σ =0,thena
n
(k)
d
≈N(nμ, nσ
2
).
A second, local limit theorem was also given by Bender.
Theorem 8.29 [18, Theorem 3] Let f(z, w) have power series expansion
f(z,w)=
n,k≥0
a
n
(k)z
n
w
k
with nonnegative coefficients a
n
(k),andleta<bbe real numbers. Define
R(ε)={ z | a ≤ Re(z) ≤ b, |Im(z)|≤ε}.
Suppose there exist ε>0, δ>0, a nonnegative integer and functions A(s)
and r(s) such that
1. A(s) is continuous and nonzero for s ∈ R(ε);
2. r(s) is nonzero and has bounded third derivative for s ∈ R(ε);
3. for s ∈ R(ε) and |z|≤|r(s)|(1 + δ)
1 −
z
r(s)
f(z,e
s
) −
A(s)
1 − z/r(s)
is analytic and bounded;
4.
r
(α)
r(α)
2
−
r
(α)
r(α)
=0 for a ≤ α ≤ b;
5. f(z, e
s
) is analytic and bounded for
|z|≤|r(Re(s))|(1 + δ) and ε ≤|Im(s)|≤π.
© 2010 by Taylor and Francis Group, LLC

328 Combinatorics of Compositions and Words
Then we have that
a
n
(k) ≈
n
e
−αk
A(α)
!r(α)
n
σ
α
√
2πn
(8.11)
as n →∞, uniformly for a ≤ α ≤ b,where
k
n
= −
r
(α)
r(α)
and σ
2
α
=
k
n
2
−
r
(α)
r(α)
.
Finally, to be able to specify growth rates easily, we will use Landau’s big
and little O notation.
Definition 8.30 We say that a function f(x) is of the order of g(x) or
O(g(x)) as x →∞if and only if there exists a value x
0
and a constant
M>0 such that |f(x)|≤M|g(x)| for all x>x
0
or, equivalently, if and only
if lim sup
x→∞
|f(x)/g(x)| < ∞. We say that f(x) is o(g(x)) if and only if
|f(x)/g(x)|→0 as x →∞, that is, f (x) grows slower than g(x) as x →∞.
In general, g(x) is a function that is simpler than f(x) and consists of the
terms that dominate the growth of f(x) in the limit.
Example 8.31 Let f(x)=3x
2
+x−1.Thenf(x)=O(x
2
) and f(x)=o(x
n
)
for n ≥ 3.
Having all the necessary tools available for the asymptotic analysis, we now
consider various statistics for compositions and Carlitz compositions.
8.4 Asymptotics for compositions
In this section we derive various asymptotic results for compositions. In
Section 8.4.1 we concentrate on compositions that avoid or contain a given
subword pattern, and derive results on the number of such compositions, the
average number of parts in such compositions, as well as asymptotic dis-
tributions for these compositions. In Sections 8.4.2 and 8.4.3 we focus on
asymptotic results for the largest part and the number of distinct parts in
compositions of n.
8.4.1 Asym ptotics for subword pattern avoidance
Avoidance of subword patterns of length two reduces either to Carlitz com-
positions (avoidance of the subword pattern 11, which will be discussed in
Section 8.5) or partitions (avoidance of the subword pattern 12). The asymp-
totic behavior for partitions is well-known and dates back to the early part of
© 2010 by Taylor and Francis Group, LLC

Asymptotics for Compositions 329
the last century. Hardy and Ramanujan in 1918, and independently Uspensky
in 1920, derived the following asymptotic result for partitions (see for example
[10] or [164]).
Theorem 8.32 Let p(n) be the number of partitions of n.Then
AC
12
(n)=p(n) ≈
e
π
√
2n/3
4n
√
3
as n →∞.
Subword patterns of length three were investigated by Heubach and Man-
sour [92]. We present the results for the eight single subword patterns 111,
112, 221, 212, 121, 123, 132 and 213, and for the patterns valley and peak.
In all cases, the process is the same, namely checking that the generating
functions are meromorphic (see Definition E.8) in a disc around the origin,
identifying the dominant singularity, checking that it is a pole of multiplicity
one, and then using Theorem 8.25 for the rate of growth. Similar analyses
for the longer subword patterns discussed in Sections 4.3.3, 4.3.4, and 4.3.5
together with results on the asymptotic distribution were given by Mansour
and Sirhan [145].
Theorem 8.33 For subword patterns τ of length three, we have that
AC
τ
(n) ≈ A
τ
(ρ
∗
τ
)
−n
,n→∞, (8.12)
where the zeros ρ
∗
τ
are given by
ρ
∗
111
=0.5233508903 ρ
∗
112
=0.5534397072
ρ
∗
221
=0.5133872872 ρ
∗
212
=0.5120333765
ρ
∗
121
=0.5386079645 ρ
∗
123
=0.5132858388
ρ
∗
132
=0.5055555128 ρ
∗
213
=0.5220916260
ρ
∗
valley
=0.543206932 ρ
∗
peak
=0.6135900256
and the constants A
τ
are given by
A
111
=0.4993008432 A
112
=0.6920054131
A
221
=0.5453621593 A
212
=0.5372331234
A
121
=0.5838933009 A
123
=0.5760960195
A
132
=0.5353097161 A
213
=0.6121896742
A
∗
valley
=0.7282070589 A
peak
=1.3945612176
Note that Theorem 8.33 for τ = 111 gives the asymptotics for the number
of 2-Carlitz compositions.
Proof Let τ be any of the ten subword patterns. Using results from Chap-
ter 4 it can be shown that the functions AC
τ
(z,w) are meromorphic in the
domain |z| < 1ifw ∈ [0, 1] and meromorphic in the domain |z| < 1/w if
© 2010 by Taylor and Francis Group, LLC
330 Combinatorics of Compositions and Words
w ∈ [1, ∞]. Thus the asymptotic behavior of AC
τ
(n) is determined by the
dominant pole of the function AC
τ
(z,1) = 1/h
τ
(z). By Theorem 8.20 this
pole occurs at the smallest positive root ρ
∗
τ
of h
τ
(z). We numerically compute
the roots ρ
∗
τ
by converting h
τ
(z) into a series up to the z
30
term. Since all
the zeros have modulus less than 0.7, we use the curve γ = {z ||z| =0.7}
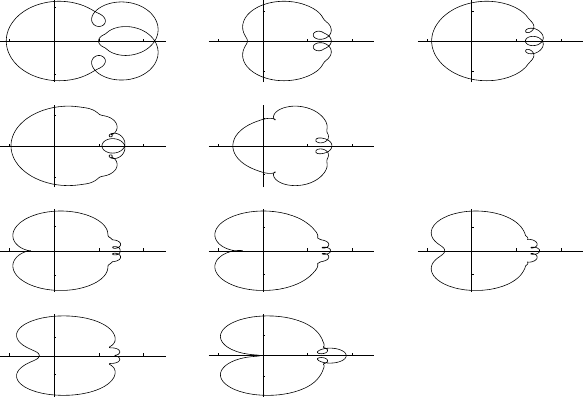
when applying Theorem 8.27. Figure 8.1 shows the curves h
τ
(γ)(inthesame
order as the zeros given in Theorem 8.33) where we have used the expansion
of h
τ
(z)uptothez
30
term.
1 1 2
1
1
Τ111
1 1 2
1
1
Τ112
1 1 2
1
1
Τ221
1 1 2
1
1
Τ212
1 1 2
1
1
Τ121
1 1 2
1
1
Τ123
1 1 2
1
1
Τ132
1 1 2
1
1
Τ213
1 1 2
1
1
Τvalley
1 1 2
1
1
Τpeak
FIGURE 8.1: Image of h
τ
(z)for|z| =0.7
In each case, the winding number is one, so that the function h
τ
(z)has
exactly one root ρ
∗
τ
in the domain |z| < 0.7. Thus, Theorem 8.25 gives (8.12)
where the values A
τ
are computed using the expansion of h(z)tothez
30
term. 2
We can also obtain results on the average number of parts in a random
composition avoiding a given subword pattern. Knopfmacher and Prodinger
[119, Section 2] derived asymptotics on the average number of parts in a ran-
dom Carlitz composition of n, thus covering the case of the subword pattern
11. More precisely, if we let X
11
par
(n) denote the number of parts in a random
Carlitz composition of n, then Knopfmacher and Prodinger showed that
E(X
11
par
(n)) ≈ 0.350571n.
© 2010 by Taylor and Francis Group, LLC

Asymptotics for Compositions 331
We derive the corresponding results for random compositions that avoid the
patterns of length three given in Table 4.2.
Theorem 8.34 Let X
τ
par
(n) denote the number of parts in a random compo-
sition of n that avoids the pattern τ. Then we have that
E(X
τ
par
(n)) ≈ C
τ
·n,
where
C
111
=1.715995518 C
112
=1.915578938
C
221
=1.990357910 C
212
=1.953193954
C
121
=1.312572461 C
123
=1.744084928
C
132
=1.784275109 C
213
=1.342234855
C
valley
=1.447227208 C
peak
=0.651749
Proof We give the proof for the pattern peak. The proofs for the other pat-
terns follow along the same lines of reasoning. Applying (8.2) in Lemma 8.14
we obtain the desired expected value by differentiating the functions
AC
τ
(z,w)=C
τ
(z,w,0)
given in Section 4.3. The value for N = C
τ
(n)=[z
n
]C
τ
(z,1, 0) can be ap-
proximated by using the results of Theorem 8.33. Specifically, for the pattern
peak we obtain from Example 4.27 that
AC
peak
(z,w)=
1+
j≥1
z
j(j+2)
w
2j
2j
i=1
(1 − z
i
)
1+
j≥1
z
j(j+2)
w
2j
2j
i=1
(1 − z
i
)
−
j≥0
z
j
2
+3j+1
w
2j+1
2j+1
i=1
(1 − z
i
)
=
n(z,w)
h(z,w)
,
and therefore,
F
peak
(z)=
∂
∂w
AC
peak
(z,w)
(
(
w=1
=
∂
∂w
n(z,w)
(
(
w=1
h(z,1) − n(z,1)
∂
∂w
h(z,w)
(
(
w=1
h(z,1)
2
.
Since it can be shown numerically that the numerator of F
peak
(ρ
∗
peak
) =0and
h(ρ
∗
peak
, 1) = 0 (that is how ρ
∗
peak
was computed), we have that for z close to
the dominant singularity ρ
∗
peak
F
peak
(z) ≈
B
peak
(1 − z/ρ
∗
peak
)
2
,
where B
peak
= lim
z→ρ
∗
peak
(1 −z/ρ
∗
peak
)
2
F
peak
(z)=0.908904458 (using Maple
with an approximation to the z
30
term). From (8.6) we then obtain that
[x
n
]F
peak
(z) ≈ B
peak
· n · (ρ
∗
peak
)
−n
,
© 2010 by Taylor and Francis Group, LLC
332 Combinatorics of Compositions and Words
and therefore, E(X
peak
par
(n)) ≈
B
peak
A
peak
· n where A
peak
is the value given in
Theorem 8.33. 2
Using Theorems 8.28 and 8.29 we can obtain a more detailed picture of
the asymptotic distribution function for the number of parts in compositions
of n (as n →∞). In fact, Flajolet and Sedgewick [68, Chapter IX.6] show
that one can obtain Gaussian limit laws for many statistics that have bivari-
ate meromorphic generating functions by using singularity perturbation on
the secondary variable. Mansour and Sirhan gave results for all three-letter
patterns and for selected patterns of length [145, Theorem 3.1].
Theorem 8.35 For large n, the number of parts M in a composition of n that
avoids τ is asymptotically Gaussian with mean nμ
τ
and standard deviation
√
nσ
τ
, that is,
M − μ
τ
n
√
nσ
τ
d
≈N(0, 1).
Furthermore,
AC
τ
N
(m; n) ≈
A
τ
(ρ
∗
τ
)
n
·
√
2πn ·σ
τ
e
−(m−nμ
τ
)
2
/(2nσ
2
τ
)
,
for m − nμ
τ
= O(
√
n),whereA
τ
and ρ
∗
τ
are given in Theorem 8.33 and μ
τ
and σ
2
τ
are given by
τ
μ
τ
σ
2
τ
111 0.4277999660 0.1654603703
112
0.4465604097 0.2471428219
221
0.4866127277 0.2498205897
212
0.4879666379 0.2498550090
121
0.4613949299 0.2484778134
123
0.4854585926 0.2606813427
132
0.5112956159 0.2517270954
213
0.5030376743 0.2777839362
.
Proof Let h
τ
(z,w)=1/AC
τ
(z,w). Then we can use Theorem 8.28 to
compute the values of r
τ
(z,w)ands
τ
(z,w) given in (8.9) and (8.10). Setting
w =1andz = ρ
∗
τ
we derive μ
τ
= −r
τ
/ρ
∗
τ
and σ
2
τ
= μ
2
τ
−s
τ
/ρ
∗
τ
,wherer
τ
and
s
τ
given below are numerically computed by developing h
τ
(z,w)intoaseries
© 2010 by Taylor and Francis Group, LLC

Asymptotics for Compositions 333
up to the z
30
term and using the values of ρ
∗
τ
given in Theorem 8.33.
τ
r
τ
s
τ
111 − 0.2238894933 0.00918608541
112
−0.2471442624 −0.02641380791
221
−0.2498207882 −0.00668873965
212
−0.2498552052 −0.00601309945
121
−0.2485109840 −0.01917042125
123
−0.2491790209 −0.01283794488
132
−0.2584883173 0.00490192258
213
−0.2626317573 −0.01291499850
.
The statement to be proven now follows from Theorem 8.29 with r(s)=r(s, 1)
as defined in Theorem 8.28, A(s)=A
τ
,and =1. Furthermore,ifm−nμ
τ
=
O(
√
n), then the assumptions of Theorem 8.29 are satisfied and the statement
about the asymptotics of AC
N
(m; n) follows. 2
Remark 8.36 Even though both Theorem 8.34 and 8.35 give results on the
asymptotics for the number of parts, one has to be careful to distinguish be-
tween them. Theorem 8.34 gives a result for a fixed large n, giving the average
number of parts over all compositions of n. Theorem 8.35 gives an asymptotic
distribution for the number of parts for cases where the order of the composi-
tion and the number of parts are of given relative size as expressed by the big
O requirement.
Results similar to those of Theorem 8.35 can also be obtained for the pat-
terns peak and valley (see Exercise 8.5) and for longer patterns (see [145]).
We conclude this section with some results on the asymptotics for the num-
ber of compositions of n containing a subword pattern τ a given number of
times. Knopfmacher and Prodinger [119] showed that the number of com-
positions of n with exactly r occurrences of the subword pattern 11 has the
asymptotic behavior
C
11
(n, r) ≈ C
r
n
r
(ρ
∗
)
−n
,
where ρ
∗
=0.571349 is the single positive real pole of CC (z)intheinterval
[0, 1] and the constants C
r
are explicitly computable. For example, the con-
stants for r =0, 1, 2aregivenbyC
0
=0.4563, C
1
=0.0482, and C
2
=0.0025.
Remark 8.37 In general, if C
τ
(z,w,q)=1/h
τ
(z,w,q) is the generating
function for the number of compositions of n with m parts according to the
number of occurrences of the subword pattern τ, then applying Taylor’s for-
mula results in
[q
r
]C
τ
(z,1,q)=
1
r!
∂
r
∂q
r
C
τ
(z,1,q)
(
(
(
(
q=0
=
G
τ
(z)
h
τ
(z,1, 0)
r+1
,
© 2010 by Taylor and Francis Group, LLC
334 Combinatorics of Compositions and Words
where G
τ
(z) is a function consisting of derivatives of h
τ
(z,1,q) evaluated at
q =0. Consequently, for fixed r and n →∞, the number of compositions with
exactly r occurrences of the subword pattern τ has asymptotic behavior
C
τ
(n, r) ≈ C
τ
r
n
s(r+1)−1
(ρ
∗
τ
)
−n
,
where ρ
∗
τ
has multiplicity s and is the smallest positive real root of h
τ
(z,1, 0).
Example 8.38 For instance, if τ = 111, then we obtain from Theorem 4.32
and Remark 8.37 that the number of compositions with exactly r occurrences
of the subword pattern 111 has the following asymptotic behavior (see Exercise
8.6):
C
111
(n, 0) ≈ 0.4993008432 · 0.5233508903
−n
,
C
111
(n, 1) ≈ 0.05827141770 ·n · 0.5233508903
−n
,
C
111
(n, 2) ≈ 0.00339555803 ·n
2
·0.5233508903
−n
.
We now leave pattern avoidance and enumeration behind and consider the
asymptotics for statistics on unrestricted compositions.
8.4.2 Asym ptotics for the largest part
In the analysis so far we either computed the average of a statistic from the
generating function using Lemma 8.14, or obtained asymptotic results using
Theorem 8.25. We now show an example where we compute the average using
a different method and in the process encounter an estimate that contains a
small periodic part, very different from the results discussed so far.
Theorem 8.39 Let X
max
(n) denote the largest part in a random composition
of n.Then,
E(X
max
(n)) ≈ log
2
n +0.3327461773 + d(log
2
n),
where d(x) is a function that has period one, mean zero, and small amplitude.
Proof Since the random variable X
max
(n) is nonnegative, we have from
Theorem D.8 that
E(X
max
(n)) =
∞
h=0
P (X
max
(n) >h)=
∞
h=0
1 −
C
[h]
(n)
C(n)
, (8.13)
where C
[h]
(n) denotes the number of compositions of n with parts in [h]=
{1, 2,...,h} (all parts are less than or equal h)andC(n)isthenumberof
compositions of n with parts in N. So we need to derive asymptotic results
for both these quantities. From Example 2.35 we have that
C(z)=
1
1 − g(z)
=
1
1 −
z
1−z
,
© 2010 by Taylor and Francis Group, LLC
Asymptotics for Compositions 335
and from Theorem 3.13 we obtain that
C
[h]
(z)=
1
1 − (z + z
2
+ ···+ z
h
)
=
1
1 −
z(1−z
h
)
1−z
=
1
1 − g
h
(z)
.
It is easy to show that C(z) has a dominant pole at ρ
∗
=1/2 of multiplicity
one, so applying Theorem 8.25 we obtain that C(n) ≈
1
ρ
∗
g
(ρ
∗
)
(ρ
∗
)
−n
.Now
let ρ
∗
h
be the smallest positive real solution of the equation g
h
(z)=1(and
therefore, the dominant pole of C
[h]
(z)). It can be shown that ρ
∗
h
is a simple
pole (see Exercise 8.7) and therefore,
C
[h]
(n) ≈
1
ρ
∗
h
g
h
(ρ
∗
h
)
(ρ
∗
h
)
−n
.
This expression is not very useful as it depends on h, so we will express
ρ
∗
h
in terms of ρ
∗
and g
h
(z)intermsofg(z). Clearly, in the disk |z| < 1,
lim
h→∞
C
[h]
(z)=C(z) and lim
h→∞
ρ
∗
h
= ρ
∗
. Following the “bootstrapping
method” described in [124], we obtain that around z = ρ
∗
,
g
h
(z) ≈ g(z) −
(ρ
∗
)
h+1
1 − ρ
∗
,
and therefore
C
[h]
(z) ≈
1
1 − g(z)+
(ρ
∗
)
h+1
1−ρ
∗
(8.14)
near z = ρ
∗
.Usingg(ρ
∗
) = 1 and Taylor’s theorem for g(ρ
∗
h
)withρ
∗
h
=
ρ
∗
(1 + ε
h
) we obtain that
0 ≈ ρ
∗
·ε
h
·g
(ρ
∗
) −
(ρ
∗
)
h+1
1 − ρ
∗
,
and therefore
ε
h
≈
1
(1 − ρ
∗
)g
(ρ
∗
)
(ρ
∗
)
h
.
Applying Theorem 8.25 to (8.14) results in
C
[h]
(n) ≈
1
ρ
∗
h
g
(ρ
∗
h
)
(ρ
∗
h
)
−n
≈
1
ρ
∗
g
(ρ
∗
)
(ρ
∗
)
−n
(1 + ε
h
)
−n
,
whereweareusingthatρ
∗
h
≈ ρ
∗
for the fraction and substitute ρ
∗
h
= ρ
∗
(1+ε
h
)
in the power term for the second approximation. Thus, the probability that
the largest part is greater than h is approximated by
1 −
C
[h]
(n)
C(n)
≈ 1 − (1 + ε
h
)
−n
≈ 1 − (1 −ε
h
)
n
≈ 1 −
1 −
1
(1 − ρ
∗
)g
(ρ
∗
)
(ρ
∗
)
h
n
. (8.15)
© 2010 by Taylor and Francis Group, LLC
