Heubach S., Mansour T. Combinatorics of Compositions and Words
Подождите немного. Документ загружается.


356 Combinatorics of Compositions and Words
Exercise 8.17
∗
Let w = w
1
w
2
···w
n
be a k-ary word of length n. We define
the total variation (or just variation) u(w)=u
n,k
(w) of w as the sum of the
differences of adjacent letters of w, that is,
u(w)=
n−1
i=1
|w
i
− w
i+1
|.
For example, the total variation of the word w = 1121415221 ∈ [5]
10
equals
u(w)=0+1+1+3+3+4+3+0+1=16.
(1) Use the scanning-element algorithm to obtain that the generating func-
tion
F
k
(x, q)=
n≥0
x
n
w∈[k]
n
q
u(w)
is given by
1+
k(1 − q)x
1 − q − x(1 + q)
−
2x
2
q
1−t
k
1−t(q)
(1 − q − x(1 + q))
%
1 − x
1−qt
k
1−qt
&
where
t =
1 − x + q
2
(1 + x) −
:
(1 − q
2
)(1 + q − x(1 − q))(1 − q − x(1 + q))
2q
.
(2) Prove that the generating function F
k
(x, q) can be expressed as
F
k
(x, q)=1+
k
i=1
(x
i
− qx
i−1
),
where
x
i
=
x(1 −q)
q
k−1
j=i
U
i−1
(s/2)
j−1
s=0
U
s
(s/2)
U
j−1
(s/2)U
j
(s/2)
+
xU
i−1
(s/2)
U
k−1
(s/2)
U
k−1
(s/2) + (1 − q)/q
k−1
j=0
U
j
(s/2)
U
k
(s/2) − q(1 + x)U
k−1
(s/2)
,
U
i
is the i-th Chebychev polynomial of the second kind (see Definition
C.1 ),ands =
1+q
2
− x(1 − q
2
)
q
.
(3) Derive from (1) that the mean and the variance of the total variation of
a randomly chosen k-ary word of length n are given by
(n − 1)(k +1)(k − 1)
3k
© 2010 by Taylor and Francis Group, LLC

Asymptotics for Compositions 357
and
(k − 1)(k +1)(k
2
(6n − 7) + 2(3n − 1))
90k
2
,
respectively.
(4) Prove (3) directly without using (1) and (2).
8.8 Research directions and open problems
We now suggest several research directions, which are motivated both by
the results and exercises of this and earlier chapter(s).
Research Direction 8.1 As shown in the previous chapter, finding either
the number of k-ary words of length n avoiding a fixed pattern or the number
of compositions of n avoiding a fixed pattern is a hard problem. A potentially
easier problem is to find the asymptotics for either the number of k-ary words
of length n avoiding a fixed pattern or the number of compositions of n that
avoid a fixed pattern. This question has been answered for words avoiding
a subsequence pattern of length three by Br¨and´en and Masour [27], and for
compositions avoiding a subsequence pattern of length three by Savage and
Wilf [176].
Find either the asymptotics for the number of words (compositions) avoiding
a fixed subsequence pattern of length four or five, or find an upper bound for
therateofgrowthforthenumberofthesewords(compositions). Obviously, we
are interested in the smallest upper bound. (The trivial bound for compositions
is 2
n
, and for words on the alphabet [k] the trivial bound is k
n
).
Research Direction 8.2 Baik, Deift, and Johansson [12] solved a problem
about the asymptotic behavior of the length X
lis
(n) of the longest increasing
subsequence for random permutations of order n as n →∞(with the uniform
distribution on the set of permutations S
n
). They proved that the sequence
X
lis
(n) − 2
√
n
n
1/6
converges in distribution, as n →∞, to a certain random variable whose
distribution function can be expressed via a solution of the Painlev´eIIequation
(see [12] for details).
More recently, the case of the longest (strongly and weakly) increasing subse-
quence in k-ary words has been studied by Tracy and Widom [187]. For exam-
ple, the word w = 1123254 has longest strongly (=strictly) increasing subse-
quence of length 4,namelyw
1
w
3
w
4
w
6
= w
2
w
3
w
4
w
6
= 1235, while the longest
(weakly) increasing subsequence is of length 5, namely either w
1
w
2
w
3
w
4
w
6
=
© 2010 by Taylor and Francis Group, LLC
358 Combinatorics of Compositions and Words
11235, w
1
w
2
w
3
w
4
w
7
= 11234, w
1
w
2
w
3
w
5
w
6
= 11225,orw
1
w
2
w
3
w
5
w
7
=
11224. The natural extension is to study the same statistic, longest (strongly
or weakly) increasing subsequence, in random compositions of n with parts in
N.
© 2010 by Taylor and Francis Group, LLC

Appendix A
Useful Identities and Generating
Functions
A.1 Useful formulas
The Binomial theorem
1
(x + y)
n
=
i≥0
n
i
x
i
y
n−i
(A.1)
is often attributed to Blaise Pascal (who described it in the 17th century) but
it was known to many mathematicians who preceded him. Around 1665, Isaac
Newton generalized (A.1) to allow exponents other than nonnegative integers.
In this generalization the finite sum is replaced by an infinite series. Namely,
if x and y are real numbers with x>|y| and r is any complex number, then
(x + y)
r
=
j≥0
r
j
x
r−j
y
j
=1+
r
1!
x
r−1
y +
r(r − 1)
2!
x
r−2
y
2
+ ··· .
In the special case where x =1andr =1/2, we obtain that
:
1+y =
m≥0
1/2
m
y
m
=1+
m≥1
(−1)
m−1
(2m − 2)!
2
2m−1
m!(m − 1)!
y
m
. (A.2)
Choosing r = −(k + 1) yields another handy formula which we will use over
and over:
1
(1 − x)
k+1
=
i≥0
k + i
k
x
i
. (A.3)
Equation (A.3) has also a nice combinatorial proof. On the left-hand side of
the equation we see a convolution of k + 1 geometric series, that is, a sum of
k + 1 nonnegative values. In how many ways can these k +1valuesaddupto
n? Well, dividing n items into k + 1 groups is the same as placing k dividers
1
http://en.wikipedia.org/wiki/Binomial theorem
359
© 2010 by Taylor and Francis Group, LLC
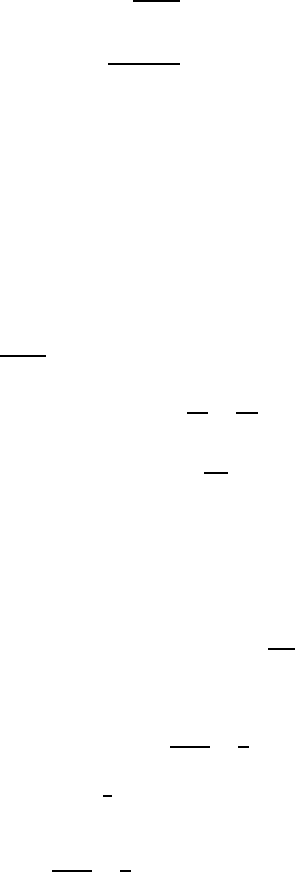
360 Combinatorics of Compositions and Words
in between the n items, that is, choosing k of the possible n + k positions for
the dividers. For example,
•••|•||••••|• ↔ 3+1+0+4+1
Equation (A.3) has two important special cases for k =0andk =1,namely
the geometric series and its derivative.
1
1 − x
=
i≥0
x
i
(A.4)
1
(1 − x)
2
=
i≥0
(i +1)x
i
(A.5)
Another handy equation that involves binomial coefficients can be easily
proved by induction on b.
a
a
+
a +1
a
+ ···+
b
a
=
b +1
a +1
(A.6)
Taylor series expansions of specific functions can be utilized for estimates
and asymptotic considerations. The approximations and the bound in the
equations below are valid for small values of x.
1
1+x
n
=(1− x + x
2
− x
3
+ ···)
n
≈ (1 −x)
n
(A.7)
e
(−x·n)
=
1 − x +
x
2
2
−
x
3
3!
+ ···
n
≈ (1 −x)
n
(A.8)
log(1 + x)=
∞
n=1
(−1)
n−1
x
n
n
<x (A.9)
Another useful identity for asymptotic estimation was proved by Hitczenko
and Stengle.
Proposition A.1 [97, Proposition 2.2] Let
f(x)=
∞
m=1
1 −
1 −
1
2
m
2
x
.
Then, for large positive k,
f(x + k)=x + k +
γ
log 2
−
1
2
+ g(x)+o(2
−x−k
),
where γ = lim
n→∞
n
i=1
1
i
− log n =0.57721566490 ··· is Euler’s constant
and
g(x)=−x −
γ
log 2
+
1
2
−
0
m=−∞
e
−2
−m+x
+
∞
m=1
(1 − e
−26−m+x
)
© 2010 by Taylor and Francis Group, LLC
Useful Identities and Generating Functions 361
is a nonconstant, mean-zero function of period 1 satisfying |g(x)|≤0.0000016.
A.2 Generating functions of important sequences
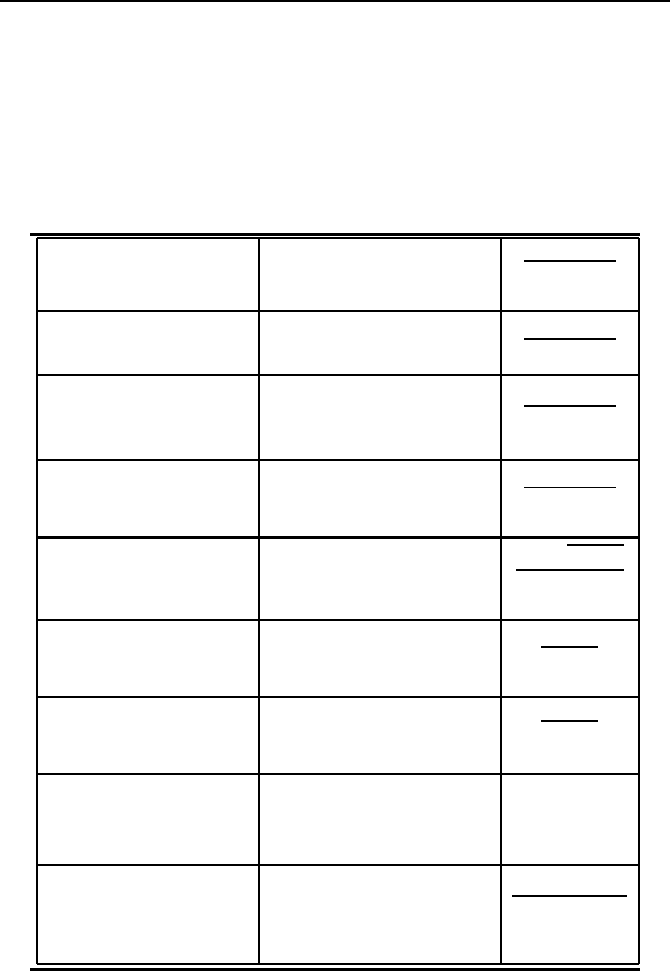
Table A.1 displays the recurrence relations and generating functions for
important sequences discussed in this text.
TABLE A.1: Generating functions of important sequences
Fibonacci F
n
= F
n−1
+ F
n−2
x
1 − x − x
2
F
0
=0,F
1
=1
Shifted Fibonacci f
n
= F
n+1
1
1 − x − x
2
Modified Fibonacci
ˆ
F
n
= F
n
for n ≥ 1
1 − x
2
1 − x − x
2
ˆ
F
0
=1
Lucas L
n
= L
n−1
+ L
n−2
2 − x
1 − x − x
2
L
0
=2,L
1
=1
Catalan C
n+1
=
n
i=0
C
i
C
n−i
1 −
√
1 − 4x
2x
C
0
=1
Compositions in N C(n)=2C(n − 1)
1 − x
1 − 2x
C(0) = C(1) = 1
Modified compositions
˜
C(n)=C(n)forn ≥ 1
x
1 − 2x
˜
C
0
=0
Stirling numbers of the
"
n +1
j
#
=
"
n
j − 1
#
+ n
"
n
j
#
n−1
i=0
(x + i)
first kind (unsigned)
"
n
0
#
= δ
n0
,
"
0
1
#
=0
Stirling numbers of the
n
k
<
=
n − 1
k − 1
<
+ k
n − 1
k
<
x
k
k
i=0
(1 − ix)
second kind
n
1
<
=
n
n
<
=1
© 2010 by Taylor and Francis Group, LLC

Appendix B
Linear Algebra and Algebra Review
B.1 Linear algebra review
Definition B.1 An n × m matrix
A =(a
ij
)=
⎡
⎢
⎢
⎢
⎣
a
11
a
12
··· a
1m
a
21
a
22
··· a
2m
.
.
.
.
.
. ···
.
.
.
a
n1
a
n2
··· a
nm
⎤
⎥
⎥
⎥
⎦
is a rectangular array of numbers consisting of n rows and m columns. An
n×n matrix is called a square matrix. The entries a
11
,a
22
,...,a
nn
are said to
be on the main diagonal of A. The sum of the elements on the main diagonal
of an n ×n matrix is called the trace of the matrix, that is
tr(A)=a
11
+ a
22
+ ···+ a
nn
=
n
i=1
a
ii
.
A matrix whose entries are all zero is called the zero matrix and denoted by
O. A square matrix whose entries on the main diagonal are 1 and whose off-
diagonal entries are 0 is called the identity matrix and denoted by I.Amatrix
whose only nonzero entries are on the main diagonal is called a diagonal
matrix.
Matrix addition and scalar multiplication of matrices are very straightfor-
ward, while matrix multiplication is a little more involved.
Definition B.2 1. For any matrix A and scalar k, k · A =(ka
ij
).
2. For two matrices A and B of the same dimensions, A ±B =(a
ij
±b
ij
).
3. Let A be an n × r matrix and B an r × m matrix. Then C = A · B is
an n × m matrix, where c
ij
=
r
k=1
a
ir
b
rj
.
363
© 2010 by Taylor and Francis Group, LLC
364 Combinatorics of Compositions and Words
Definition B.3 If A is an n×n matrix, then the (unique) n×n matrix B
such that
AB = BA = I =
⎡
⎢
⎢
⎢
⎣
100··· 0
010··· 0
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
000··· 1
⎤
⎥
⎥
⎥
⎦
is called the inverse of A and denoted by A
−1
.
Definition B.4 If A is any n × m matrix, then the transpose of A,denoted
by A
T
, is defined to be the m × n matrix that results from interchanging the
rows and columns of A, that is, A
T
=(a
ji
).
Definition B.5 The determinant det(A) of an n × n matrix A =(a
ij
) is a
scalar which can be computed using Leibnitz’ formula:
det(A)=
π∈S
n
sgn(π)
n
i=1
a
i,π
i
,
where π is a permutation, and sgn(π)=1if π is an even permutation, and
sgn(π)=−1 if π is an odd permutation. (A permutation is even if it can be
obtained from 123 ···n by an even number of exchanges of two numbers, and
odd otherwise.)
Example B.6 The permutation π = 321 is an odd permutation as there is
one pairwise exchange, namely switching 1 and 3 to obtain π from 123.
The above definition of the determinant is mainly used for 2 × 2and3×3
matrices. In the case of a 2 × 2 matrix, the general formula reduces to
det(A)=det
"
a
11
a
12
a
21
a
22
#
= a
11
a
22
− a
21
a
12
(B.1)
since there are two permutations 12 and 21 in S
2
.For3×3 matrices, summing
over the six permutations of 123 (of which three are odd and three are even),
we obtain that
det(A)=a
11
a
22
a
33
+ a
12
a
23
a
31
+ a
13
a
21
a
32
− a
11
a
23
a
32
− a
12
a
21
a
33
− a
13
a
22
a
31
. (B.2)
This formula is easily remembered as follows: extend the 3 × 3matrixby
appending the first two columns at the right end. Then the positive factors
are exactly the products of the entries on the three diagonals from top left to
bottom right, and the negative factors are the products of the entries on the
three diagonals from bottom left to top right, as shown in Figure B.1.
© 2010 by Taylor and Francis Group, LLC

Linear Algebra and Algebra Review 365
+
a
11
a
21
a
31
−
+
a
12
a
22
a
32
−
+
a
13
a
23
a
33
−
a
11
a
21
a
31
a
12
a
22
a
32
FIGURE B.1: Determinant computation for 3 ×3 matrices.
Example B.7 Let A =
⎡
⎣
123
253
108
⎤
⎦
.Then
det(A)=1· 5 · 8+2· 3 · 1+3· 2 · 0 − (1 · 5 · 3+0· 3 · 1+8· 2 · 2)
=46− 47 = −1.
A more commonly used way to compute the determinant of a matrix, es-
pecially for large matrices, is the use of cofactors.
Definition B.8 If A is a square n×n matrix, then the minor of entry a
ij
is
denoted by M
ij
and is defined to be the determinant of the submatrix that
remains after the i-th row and the j-th column are deleted from A.The
cofactor of entry a
ij
is denoted by C
ij
and is computed as C
ij
=(−1)
i+j
M
ij
.
The matrix
⎡
⎢
⎢
⎢
⎣
C
11
C
12
··· C
1n
C
21
C
22
··· C
2n
.
.
.
.
.
.
.
.
.
C
n1
C
n2
··· C
nn
⎤
⎥
⎥
⎥
⎦
is called the matrix of cofactors from A. The transpose of the cofactor matrix
is called the adjoint of A and is denoted by adj(A), that is
adj(A) =
⎡
⎢
⎢
⎢
⎣
C
11
C
21
··· C
n1
C
12
C
22
··· C
n2
.
.
.
.
.
.
.
.
.
C
1n
C
2n
··· C
nn
⎤
⎥
⎥
⎥
⎦
.
Example B.9 For the matrix A given in Example B.7, the cofactors are
© 2010 by Taylor and Francis Group, LLC
366 Combinatorics of Compositions and Words
given by
C
11
=(−1)
1+1
det
"
53
08
#
=40,C
12
=(−1)
1+2
det
"
23
18
#
= −13,
C
13
=(−1)
1+3
det
"
25
10
#
= −5,C
21
=(−1)
2+1
det
"
23
08
#
= −16,
C
22
=(−1)
2+2
det
"
13
18
#
=5,C
23
=(−1)
2+3
det
"
12
10
#
=2,
C
31
=(−1)
3+1
det
"
23
53
#
= −9,C
32
=(−1)
3+2
det
"
13
23
#
=3,
C
33
=(−1)
3+3
det
"
12
25
#
=1.
Thus,
adj(A) =
⎡
⎣
C
11
C
21
C
31
C
12
C
22
C
32
C
13
C
23
C
33
⎤
⎦
=
⎡
⎣
40 −16 −9
−13 5 3
−521
⎤
⎦
.
Theorem B.10 The determinant of an n × n matrix A can be computed by
multiplying the entries in any row (or column) by their cofactors and adding
the resulting products. That is, for each 1 ≤ i ≤ n and 1 ≤ j ≤ n,wecan
compute the determinant via the cofactor expansion along the i-th row:
det(A)=a
i1
C
i1
+ a
i2
C
i2
+ ···+ a
in
C
in
or via the cofactor expansion along the j-th column:
det(A)=a
1j
C
1j
+ a
2j
C
2j
+ ···+ a
nj
C
nj
.
Example B.11 (Continuation of Example B.9). We can use the cofactors
computed in Example B.9 to compute the determinant of the matrix A given
in Example B.7 in a different way. For example, using the cofactor expansion
along the first row, we obtain
det(A)=a
11
C
11
+ a
12
C
12
+ a
13
C
13
=1·40 + 2 · (−13) + 3 · (−5) = −1.
Using the cofactor expansion along the second column gives
det(A)=a
12
C
12
+ a
22
C
22
+ a
32
C
32
=2·(−13) + 5 ·5+0· 3=−1.
Note that it is advantageous to use rows or columns of A that have zero entries
(requires computation of fewer cofactors).
Another use of cofactors and the adjoint matrix is the computation of the
inverse of a matrix.
© 2010 by Taylor and Francis Group, LLC
