Heubach S., Mansour T. Combinatorics of Compositions and Words

Подождите немного. Документ загружается.

Using Mathematica



and Maple

389

F.1.4 Solving recurrence relations

The function RSolve[eqn,a[n],n] solves a recurrence relation for a[n].

A more general version solves a system of recurrence relations or a partial

recurrence relation. We illustrate the function RSolve with the recurrence for

the Fibonacci sequence:

RSolve[{f[n+2]==f[n+1]+f[n],f[0]==0,f[1]==1},f[n],n]

This results in

that is, Mathematica recognizes this as the recurrence for the Fibonacci se-

quence. In order to obtain a generating function from a recurrence rela-

tion, we apply the function GeneratingFunction to the result of RSolve.

GeneratingFunction[expr,n,x] gives the generating function in x for the

sequence whose n-th series coeﬃcient is given by the expression expr.Forex-

ample, to obtain the generating function from the recurrence of the Fibonacci

sequence, we use

sol=RSolve[{f[n+2]==f[n+1]+f[n],f[0]==0,f[1]==1},f[n],n];

GeneratingFunction[sol[[1,1,2]],n,x]//Simplify

This results in

-(x/(-1+x+x^2))

If we have already derived a generating function for a sequence then we

can try to obtain an explicit formula for the coeﬃcients a

in terms of n by

using the function SeriesCoefficient. Its syntax is basically the same as

Series, except we enter n instead of an integer value indicating the order of

the expansion. For the Fibonacci sequence we use

SeriesCoefficient[x/(1-x-x^2),{x,0,n}]

This returns the familiar formula for the Fibonacci sequence.



−

(

1−

√

))

(

√

))

√

n ≥ 0

0True

F.1.5 Obtaining results from sequence values

In Version 7.0 of Mathematica, several new functions were introduced. They

all take as input a list of sequence values and then try to ﬁnd either an

explicit formula, a recurrence relation, or a generating function. We give some

examples of these functions using either the ﬁrst few values of the Fibonacci

sequence or the ﬁrst few values of the Catalan sequence as our starting point.

First let’s ﬁnd a recurrence relation:

FindLinearRecurrence[{1,1,2,3,5,8,13,21}]

390 Combinatorics of Compositions and Words

which returns the kernel (the list of coeﬃcients) of the shortest recurrence

relation that creates these values:

{1,1}

This means that the recurrence relation is of the form a

=1·a

n−1

+1·a

n−2

We can recreate the sequence by using LinearRecurrence[ker, init, n]

which gives the sequence of length n obtained by iterating the linear recurrence

with kernel ker and initial values init:

LinearRecurrence[{1,1},{1,1}, 8]

The output is our original sequence:

{1,1,2,3,5,8,13,21}

Next we look at ﬁnding the generating function from a sequence of val-

ues. FindGeneratingFunction[{a1,a2,...}, x] attempts to ﬁnd a simple

generating function in x whose n-th series coeﬃcient is a

FindGeneratingFunction[{1,1,2,5,14,42,132,429,1430},x]

which returns

2/(1+Sqrt[1-4x])

And ﬁnally there is the function FindSequenceFunction[list,n] which

attempts to ﬁnd a formula for the n-th entry in the list.

FindSequenceFunction[{1,1,2,3,5,8,13,21},n]

which returns once more

Fibonacci[n]

F.1.6 Pattern matching

Mathematica has good capabilities for pattern matching. All we need to

do is to translate the structure of the pattern that we want to ﬁnd in either

compositions or words into Mathematica patterns. For example, the subword

pattern 112 has structure ?xxy? where ? can be any integer(s) and x needs

to be less than y.InMathematica terminology this becomes

{___,x_,x_,y_,___}/; x < y

where the ___ stands for any (possibly empty) pattern, and x_ and y_ are

patterns that need to be in the relation speciﬁed by the condition that follows

/;. For a subsequence pattern there are no adjacency requirements, and

therefore, the Mathematica pattern corresponding to the subsequence pattern

112 would be

{___,x_,___,x_,___,y_,___}/; x < y

Using Mathematica



and Maple

391

This idea can be extended to patterns on a larger alphabet. For example,

the subsequence pattern 132 is coded as follows (where && denotes the logical

AND):

{___,x_,___,y_,___,z_,___}/; x < z && z<y

We use the function Position[list,pattern] to ﬁnd where in a list of ob-

jects the pattern occurs. For example, if we want to ﬁnd the subsequence

pattern 132 in the list {{1, 2, 3, 4}, {1, 4, 2, 3, 5}, {1, 5, 4}, {1, 1, 1, 1}} we use:

Position[{{1,2,3,4},{1,4,2,3,5},{1,5,4},{1,1,1,1}},

{___,x_,___,y_,___,z_,___} /; x < z && z < y]

which returns as answer the list

{{2},{3}}

This means that the pattern was detected in the second and third element of

the list. Since the result is a list, we can count the number of elements in the

list by using the function Length:

Length[{{2},{3}}]

which returns 2 as an answer. Thus two of the four entries of the original list

contained the subsequence pattern 132. Note that each word or composition

has to be expressed as a list, the the dominant structure in Mathematica.

However, the function used to create compositions renders them exactly in

this form. Now we can obtain the number of compositions that avoid a given

pattern by taking the total number of compositions and subtracting from it

the number of compositions that contain the pattern. For an example of

enumeration by direct pattern matching check out Example 5.14.

F.1.7 Random compositions

Mathematica has several built-in functions that are useful for creating ran-

dom compositions and computing probabilities. To select an element at

random from a list of values or list of compositions, use RandomChoice.

RandomChoice[vals,n] gives a list of n pseudorandom choices from the list

vals. Note that each value is equally likely to be chosen and a value can be

chosen more than once. For example, to obtain 10 random compositions of

n =5,weuse

comps[n_] := Flatten[Map[Permutations,IntegerPartitions[n]],1]

RandomChoice[comps[5],10]

which produces an answer similar to {{3, 2}, {3, 1, 1}, {2, 1, 1, 1}, {2, 1, 1, 1},

{2, 1, 2}, {1, 2, 1, 1}, { 3, 1, 1}, {3, 1, 1}, {1, 2, 2}, { 1, 1, 2, 1}}.Eachtimethis

command is executed, a diﬀerent answer will result.

Mathematica has also many functions relating to discrete and continuous

random variables. Probability mass functions and density functions are com-

puted using PDF[dist,x]. To see a list of all the built-in distributions, use

392 Combinatorics of Compositions and Words

?*Distribution. For our purposes, the Binomial and geometric distribu-

tions are the most relevant, and they are named BinomialDistribution and

GeometricDistribution. To create random values from a distribution, the

function RandomInteger is used. For example, to create ten random values

from a geometric random variable (which counts the number of trials until

the ﬁrst success) with parameter p =1/3, we use

Table[RandomInteger[GeometricDistribution[1/3]]+1,{10}]

which produces an answer similar to {1, 1, 5, 6, 1, 3, 7, 3, 4, 1}. Note that the

function GeometricDistribution produces values that count the number of

failures before the ﬁrst success, so one needs to add a 1 to obtain the number

of trials until the ﬁrst success used in the model for the random compositions.

F.2 Maple

functions

In this section we focus on Maple functions that are useful for or speciﬁc to

combinatorial enumeration. We provide a compact overview of these functions

and how they are applied. A few general remarks: code that is followed by

a : does not return its output, while code followed by ; does return the

output. Functions that exist in packages can only be used after ﬁrst loading

the package using the function with(package).

F.2.1 General functions

Here we list a number of general functions that are not speciﬁc to combina-

torics but play an important supportive role. The functions sum(f, k=m..n)

and product(f, k=m..n) compute the sum f(m)+···+f (n) and the product

f(m) ···f(n), respectively. To compute the sum and the product of the ﬁrst

ﬁve square numbers we use

sum(k^2, k=1..5);

product(k^2, k=1..5);

which returns 55 for the sum and 14400 for the product. Another very useful

function is simplify(expr) which applies various simpliﬁcation rules to expr.

For example,

simplify(1/(1-x)/(1-2*x)+x/(1-2*x));

returns

-(-1-x+x^2)/(-1+x)/(-1+2*x)

Solving systems of equations is usually tedious by hand and prone to algebraic

error. We can use solve(eqns,vars) to solve the system eqns in the variables

vars. To solve the system of three equations u + v + w =1,3u + v =3,and

u − 2v − w =0intermsofu, v,andw,weuse

Using Mathematica



and Maple

393

eqns:= {u+v+w=1,3*u+v=3,u-2*v-w=0}: vars:={u,v,w}:

solve(eqns,vars);

which results in

{v=3/5, u=4/5, w=-2/5}

We will also frequently encounter the binomial coeﬃcients





.Therelevant

Maple function is binomial(n,m). For example

binomial(10,5);

returns 252. Finally, there is a function to create the values of a sequence if

an explicit formula for its coeﬃcients is known. The function seq(f,i=m..n)

generates the sequence f(m),f(m +1),...,f(n). For example, the sequence

of the third to tenth powers of two are computed as

seq(2^i,i=3..10);

with output

8,16,32,64,128,256,512,1024

F.2.2 Series manipulation

Maple has a number of functions that deal with series expansions. The

most general of these is the function series(f,x=a,m+1) which generates the

power series expansion of f about the point x = a to order (x − a)

.To

see the ﬁrst six terms of the power series of the shifted Fibonacci sequence

f(x)=

1−x−x

(see Table A.1) about x =0weuse

series(1/(1-x-x^2),x=0,6);

resulting in the output

1+x+2*x^2+3*x^3+5*x^4+8*x^5+O[x]^6

More speciﬁc series expansions are the Taylor series expansions for one or

more variables. For a single variable we use taylor(f,x=a,n) which gives

the Taylor series expansion of the function f around x = a up to order n.

For several variables we use mtaylor(f, v, n) which computes a truncated

multivariate Taylor series expansion of the function f with respect to the

variables v to order n. By default, the expansion is about the origin, but a

diﬀerent point for expansion can be speciﬁed as an optional argument. For

example, the Taylor series of f(x)=1/(1 −x −y)aboutx =0toorder10is

computed as

taylor(1/(1-x),x=0,10);

with output

1+1*x+1*x^2+1*x^3+1*x^4+1*x^5+1*x^6+1*x^7+1*x^8+1*x^9+O(x^10)

394 Combinatorics of Compositions and Words

The multivariate Taylor expansion of f(x)=1/(1 − x − y)about(x, y)=

(0, 0) to order 3 is computed as

mtaylor(1/(1-x-y), [x,y], 4);

which results in

1+x+y+x^2+2*y*x+y^2+x^3+3*y*x^2+3*y^2*x+y^3

Usually we are interested in the coeﬃcients of the generating functions.

We can obtain these by using the function coeff(p,x,n) which extracts the

coeﬃcient of x

in the polynomial p. For example, if we are interested in

ﬁnding

]



1 − x −

√

1 − 2x − 3x



then we use

series((1-x-sqrt(1-2*x-3*x^2))/2/x^2,x=0,8);

coeff(%,x,5);

to obtain the output

1+x+2*x^2+4*x^3+9*x^4+21*x^5+51*x^6+127*x^7+O[x]^8

Note that the % sign refers to the immediate last output (which may be

nonsense if there was a syntax error in the code, so beware). The two com-

mands may be combined as

coeff(series((1-x-sqrt(1-2*x-3*x^2))/2/x^2,x=0,8),x,5);

and now the output consists of only the value 21.

If we want to get the coeﬃcients of an exponential generating function then

we need to take into account the factorial factor. Say the function to be

considered is f(x)=e

−1

and we would like to ﬁnd [x

]f(x). Then we enter

5!*coeff(series(exp(exp(x)-1),x=0,6),x,5);

to obtain the answer 52.

F.2.3 Solving recurrence relations

The function rsolve(eqns,fcns) attempts to solve the recurrence rela-

tion(s) speciﬁed in eqns for the functions in fcns, returning an expression

for the general term of the function. The ﬁrst argument should be a single

recurrence relation or a set of recurrence relations and boundary conditions.

Any expressions in eqns which are not equations will be understood to be

equal to zero. The second argument fcns indicates the functions that rsolve

should solve for. We use the recurrence relation of the Fibonacci sequence to

check out this function. Note that the recurrence and the initial conditions

have to be entered as a list.

Using Mathematica



and Maple

395

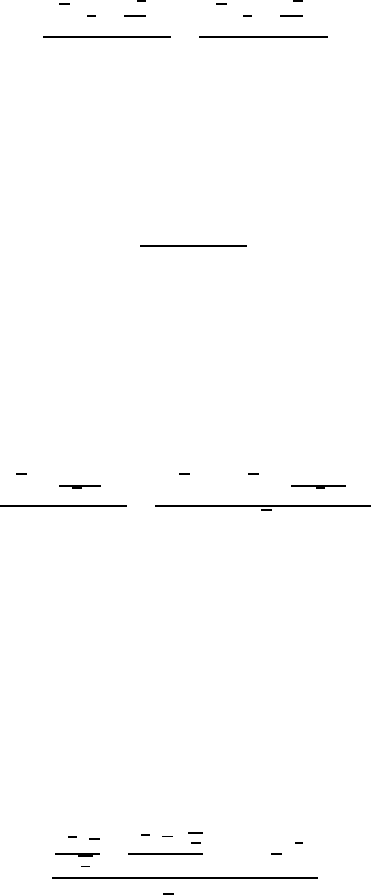
rsolve({f(n+2)=f(n+1)+f(n),f(0)=0,f(1)=1},f);

This results in

√

−

√

−

√

which is of course the explicit formula for the n-th Fibonacci number. To

obtain the generating function from the recurrence relation, we use a more

general version of rsolve.

rsolve({f(n) = f(n-1)+f(n-2), f(0)=1,(1)=1},f,’genfunc’(x));

The answer is what we expect:

−

−1+x + x

If we have derived a generating function for a sequence then we can try to

obtain an explicit formula for the coeﬃcients a

in terms of n by using the

function rgf_expand in the package genfunc. We use again the Fibonacci

sequence for illustration.

with(genfunc): rgf_expand(x/(1-x-x^2), x, n);

This returns

√

−

√

5+1

−

(

√

5 − 1)

√

−

√

5+1

5(−

√

5+1)

which needs to be manipulated a bit with the function simplify to obtain

the familiar expression for the n-th term of the Fibonacci sequence.

F.2.4 Asymptotic behavior

The function asympt(f,x,n) computes the asymptotic expansion of f with

respect to the variable x as x →∞. The third argument n speciﬁes the

truncation order of the series expansion. For instance, if we enter

asympt(n!,n,2);

we will get the output

√

+ O









As another example of the use of asympt we look at the well-known limit

sin(x)/x → 1asx → 0. How quick is this convergence? Since asympt only

works when the variable tends to inﬁnity, we rewrite the function in terms of

1/x and compute

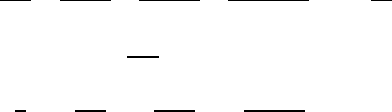
396 Combinatorics of Compositions and Words

asympt(sin(1/x)x,x,10);

The answer returned is

1 −

120x

−

5040x

362880x

+ O





This implies that the function

sin x

has asymptotic behavior

1 −

120

−

5040

362880

+ O(x

)

when x → 0.

F.2.5 Gfun Maple

package

The package Gfun was created to assist in ﬁnding generating functions.

Given the ﬁrst few coeﬃcients of a sequence, the package helps us to conjecture

the corresponding generating function. In some cases the answer will be an

explicit formula. However, most of the time such a formula does not exist

and the answer will be an equation satisﬁed by the generating function in

question. Full details on the package Gfun can be found at

http://hal.inria.fr/docs/00/07/00/25/PDF/RT-0143.pdf.

We show some examples to give the reader an idea of what is to be found

in the Gfun package. First we load the package

with(gfun);

Now let’s explore what we get if we use the ﬁrst few terms of the Fibonacci

sequence, namely 0, 1, 1, 2, 3, 5, 8, 13 as our starting point. The simplest task

is to convert the sequence into a series:

F1:=listtoseries([0,1,1,2,5,8,13],x,ogf);

which results in

F1:=x+x^2+2x^3+5x^4+8x^5+13x^6+O(x^7)

This is not a hard task, so let’s do something more challenging. To ﬁnd the

ordinary generating function for this sequence we enter

listtoratpoly([0,1,1,2,3,5,8,13],x);

and we obtain the generating function for the Fibonacci sequence

[-\frac{x}{-1+x+x^2}, ogf]

Another approach is to look for a diﬀerential equation that is satisﬁed by

the generating function for the sequence. In this case we use

listtodiffeq([0,1,1,2,3,5,8,13],y(x));

Using Mathematica



and Maple

397

which returns

[x+(-1+x+x^2)y(x), ogf]

That is, the ordinary generating function satisﬁes the diﬀerential equation

x +(−1+x + x

)y(x)=0orequivalently,y(x)=

1−x−x

. This diﬀerential

equation is particularly simple (no derivatives involved!), so we present a more

typicalexample. Weusetheﬁrstfewvalues of the Catalan sequence as the

input to listtodiffeq,thatis

listtodiffeq([1,1,2,5,14,42,132,429,1430],y(x));

The result

[{-1+(1-2x)y(x)+(x-4x^2)diff(y(x),x), y(0) = 1, ogf]

suggests that the Catalan sequence may satisfy the diﬀerential equation

1 − (1 − 2x)y(x) − (x − 4x



(x)=0

with initial condition y(0) = 1. Finally, we can ask for a recurrence relation

for the generating function for the Catalan sequence:

listtorec([1,1,2,5,14,42,132,429,1430],a(n));

We obtain that

[{a(0) = 1, (-4n-2)a(n)+(n+2)a(n+1)}, ogf]

which gives a conjecture that the Catalan numbers satisfy the recurrence

relation (n +2)a(n +1)− (4n +2)a(n) = 0 with initial condition a(0) = 1

(Prove it!!).

F.2.6 Random compositions

Maple has a package that can create all the compositions of n,namely

combinat. The function composition(n,i) produces the compositions of n

with i parts. The function rand(1..k) produces a pseudorandom integer in

the range 1,...,k. For example, to obtain 10 random compositions of n =5,

we use

with(combinat): n:=5:

a:=composition(n,1):

for i from 2 to n do

a:=a union composition(n,i):

od:

nn:=rand(1..2^(n-1)):

for s from 1 to 10 do

a[nn()];

od;

398 Combinatorics of Compositions and Words

which produces an answer similar to [1, 3, 1], [2, 3], [1, 2, 2], [1, 1, 1, 1, 1], [1, 1, 3],

[1, 1, 1, 1, 1], [2, 1, 2], [1, 1, 1, 1, 1], [1, 1, 1, 2], [1, 2, 1, 1]. Each time this com-

mand is executed, a diﬀerent answer will result.

Maple has also many functions relating to discrete and continuous random

variables. To access these, load the package Statistics. For our purposes,

the Binomial and geometric distributions are the most relevant, and they are

named Binomial and Geometric. To create random values from a distribu-

tion, the function RandomVariable is used. For example, to create ten random

values from a geometric random variable (which counts the number of trials

until the ﬁrst success) with parameter p =1/3, we use

with(Statistics):

Y := RandomVariable(Geometric(1/3))+1;

Sample(Y,10);

which produces for example the sequence 2, 5, 1, 2, 10, 6, 2, 3, 5, 3. Note

that the function Geometric in Maple counts the number of failures before

the ﬁrst success, so one needs to add a 1 to obtain the number of trials until

the ﬁrst success used in the model for the random compositions.