Heubach S., Mansour T. Combinatorics of Compositions and Words

Подождите немного. Документ загружается.

Chapter 7

Automata and Generating Trees

7.1 History and connections

In this chapter we will discuss interrelated methods that are variations

on the same theme, namely, ways to build sequences recursively and to then

express the recursive structure in an associated graph. To apply this approach

one has to construct a bijection between the objects in the question and walks

in an appropriate edge-weighted directed multi-graph. To lay a foundation

we provide the necessary graph theoretic background in Section 7.2.

The ﬁrst approach we will discuss is an automaton (plural automata). This

construct is widely used in computer science in connection with grammars

and languages. Br¨and´en and Mansour [27] were the ﬁrst to apply automata

to the enumeration of words avoiding subsequence patterns. They proved

structural results that showed that the associated graphs have only ﬁnitely

many vertices, and adapted the transfer matrix method to automata. The

name transfer matrix method was coined by West in his thesis [191], and

subsequently used by Stanley in his text [182] that has become the bible in

enumerative combinatorics. The transfer matrix method uses the adjacency

matrices of graphs to solve enumeration problems in combinatorics.

Br¨and´en and Mansour [27] obtained asymptotic results for AW

[k]

(n) for any

subsequence pattern τ using the transfer matrix method. In addition, Man-

sour implemented two programs, TOU

AUTO and TOU FORMULA, which

produce explicit results for the generating functions AW

[k]

(n), limited only

by computational power. However, the most interesting result comes from

the structure of the automaton of the increasing patterns τ



=12···( +1),

which allowed Br¨and´en and Mansour to give an alternative proof for Regev’s

result [169] on the asymptotic behavior of AW



[k]

(n). They provided a combi-

natorial proof which is based on a bijection between paths in the automaton

and certain Young tableaux. We conclude Section 7.3 by describing how the

automata for words avoiding a single pattern can be generalized to avoidance

of patterns in compositions, as well as avoidance of sets of patterns in either

words or compositions.

In Section 7.4 we discuss the second approach, generating trees, which con-

sists of deﬁning recursive rules that induce a tree. Generating trees were

introduced by West [191] who used them to enumerate permutations avoiding

245

246 Combinatorics of Compositions and Words

certain subsequence patterns. Even though the two approaches look rather

diﬀerent at ﬁrst, each generating tree (which usually has inﬁnitely many ver-

tices) can be mapped to a graph with a ﬁnite number of vertices in the form of

an automaton. Using several examples, we describe how a recursive creation

for the sequence translates into recursive rules and labels for the vertices of

the tree.

We conclude this chapter by discussing the ECO method, which is a frame-

work for describing processes to obtain recurrences for enumerating combina-

torial objects. In essence, it is a road map (much like the Noonan-Zeilberger

algorithm) in that it lays out the task to be done, but does not give a formu-

laic description of the steps. Essentially the same idea (but not with the name

ECO method) was introduced in 1978 by Chung et al. [54] who enumerated

Baxter permutations (permutations avoiding both 2-41-3 and 3-14-2) using a

generating tree. In 1995, Barcucci and several co-authors presented the ﬁrst

enumerative application of the ECO method [14], enumerating Motzkin paths

and various other combinatorial objects. Soon thereafter, these authors es-

tablished a general methodology for plane tree enumeration [15], followed by

a survey on the general theory [16]. We refer the interested reader to [16] and

[63] for further details and results, concentrating here on the ECO method as

applied to the enumeration of words and compositions. We will present the

ECO method and results of a recent paper of Bernini at el. [23] who applied

the method to pattern avoidance of pairs of generalized patterns in words, in

Section 7.5.

7.2 Tools from graph theory

For all the topics in this chapter we need to be ﬂuent in the basics of graph

theory. We start with deﬁnitions and examples from basic graph theory and

give results (without proof) that we need for our purpose. These deﬁnitions

and theorems can be found in any standard text on graph theory, see for

example [59].

Deﬁnition 7.1 A (nondirected) graph G =(V,E) consists of a set V of

vertices and a set E ⊆ V

of edges, each of which connects two vertices. We

denote an edge connecting vertices i and j by (i, j) or ij, where the order in

which the vertices are written does not matter. Two vertices i, j ∈ V are said

to be adjacent if the edge (i, j) belongs to E.Theneighborhood of a vertex

i ∈ V , denoted by N (i), is the set of all vertices adjacent to vertex i, that is,

N(i)={j | (i, j) ∈ E}.Thedegree of a vertex is the size of its neighborhood,

denoted by deg(i)=|N (i)|.

Automata and Generating Trees 247

The graphs we will encounter when discussing automata are a bit more

general. They may have multiple edges between vertices, edges from a vertex

to itself, or vertices with a direction and a weight.

Deﬁnition 7.2 A directed graph or digraph is a graph in which the edges

have a direction, that is, the edge (i, j) is diﬀerent from the edge (j, i).Anedge

is called a loop if it connects a vertex with itself. A multi-graph is a graph that

has multiple edges between a pair of vertices and also can have loops. A graph

without multiple edges and loops is called a simple graph.Theneighborhood of

avertexi in a digraph consists of out-neighbors N

(i)={j ∈ V | (i, j) ∈ E}

and in-neighbors N

−

(i)={j ∈ V | (j, i) ∈ E} , respectively. A vertex has both

an out-degree deg

(i)=|N

(i)| and an in-degree deg

−

(i)=|N

−

(i)|.

To depict a graph we use dots for the vertices, and lines connecting the

dots for the edges. If a graph is directed, then we indicate the direction by

an arrow on the edge, where the directed edge (i, j) is drawn with the arrow

pointing from i to j. When drawing a graph, it does not matter where the

vertices are located and how the edges are connected.

•



•





FIGURE 7.1: Simple graph, multi-graph, and digraph.

Example 7.3 Figure 7.1 depicts a simple graph G

with V = {1, 2, 3, 4}

and E = {(1, 2), (2, 3), (2, 4), (3, 4)}. The degrees are given by deg(1) = 1,

deg(2) = 3,anddeg(3) = deg(4) = 2. The graph G

is a multi-graph, as

there are two edges connecting vertices 2 and 4. G

is a digraph with vertex

set V = {1, 2, 3, 4} and edge set E = {(1, 2), (2, 3), (2, 4), (3, 2), (4, 4)}.The

neighbors of vertex 3 in G

are the vertices 2 and 4, while vertex 3 in graph

has in-neighbor 2 and out-neighbor 2,andthus,deg

(3) = deg

−

(3) = 1.

The idea that the visualization of a graph is irrelevant to its structure is

made precise with the notion of graph isomorphism.

Deﬁnition 7.4 Two graphs G =(V,E) and G



=(V



) are said to be

isomorphic if there exists a bijection f : V → V



such that (i, j) ∈ E if and

only if (f(i),f(j)) ∈ E



. In other words, two graphs are isomorphic if they

are really the same graph labeled or drawn in two diﬀerent ways.

Figure 7.2 presents the four nonisomorphic simple graphs on three vertices.

248 Combinatorics of Compositions and Words

•



FIGURE 7.2: The nonisomorphic simple graphs on three vertices.

Deﬁnition 7.5 We say that a graph G



=(V



) is a subgraph of the graph

G =(V,E) if V



⊆ V and E



⊆ E.

Example 7.6 The graph G



=({1, 2, 4}, {(1, 2), (2, 4)}) is a subgraph of both

the graphs G

and G

of Figure 7.1.

Besides the graphical representation, we can use a matrix to encode the

structure of the graph.

Deﬁnition 7.7 For a graph G with n vertices, we deﬁne the adjacency matrix

of G by A =(a

)

n×n

,wherea

is the number of edges from vertex i to vertex

j. The labeling of rows and columns has to be in the same order, and is done

in the obvious manner (row 1 corresponds to vertex v

,etc.).

Example 7.8 The adjacency matrices of the graphs shown in Figure 7.1 are

given by

⎡

⎢

⎣

0100

1011

0101

0110

⎤

⎥

⎦

⎡

⎢

⎣

0100

1012

0101

0210

⎤

⎥

⎦

, and A

⎡

⎢

⎣

0100

0011

0100

0001

⎤

⎥

⎦

Note that adjacency matrices of nondirected graphs are symmetric, and

that for simple graphs, the adjacency matrix contains only zeros and ones,

and the entries on the main diagonal are all zero.

Deﬁnition 7.9 A walk from vertex i to vertex j in a graph G =(V, E) is a

sequence of vertices v

···v

such that v

= i, v

= j,and(v

p+1

) ∈ E

for p =0, 1,...,k − 1. A walk where the only allowed repetitions are from

loops, that is, v



= v



only if 

= 

± 1,iscalledaloop path,andawalk

without any repeated vertices is called a path. Instead of v

···v

,wemay

also use the notation v

→v

→···→v

.Thelength of a walk is deﬁned to be

k, the number of edges in the walk. The distance between two vertices i, j ∈ V ,

denoted by d(i, j), is the length of the shortest path between them. If there is

no path between two vertices, then their distance is deﬁned as d(i, j)=∞.

A closed path,orcycle, is a path where the ﬁrst and last vertices are equal,

and those are the only repeated vertices. A graph without any cycles is called

acyclic.

Automata and Generating Trees 249

In the applications that follow, we will only encounter paths and loop paths,

and will refer to them (in an abuse of notation) simply as paths, as opposed

to writing (loop) paths all the time. If we want to emphasize that we are

actually talking about a genuine path, we will use the term simple path.

Example 7.10 In the graph G

of Figure 7.1, 1 → 2 → 4 → 3 isapathof

length three. The distances between pairs of vertices are given by d(1, 2) = 1,

d(1, 3) = d(1, 4) = 2 and d(2, 3) = d(2, 4) = d(3, 4) = 1.

In fact, we can reach every vertex from every other vertex in the graph G

This is an important property for graphs and will feature prominently in the

deﬁnition of a tree.

Deﬁnition 7.11 The graph G =(V, E) is said to be connected if for any two

vertices i, j ∈ V there exists a path from i to j. A graph that is not connected

can be partitioned into components, each of which is a maximal connected

subgraph.

Example 7.12 Graphs G

and G

in Figure 7.1 are connected, while graph

has three components: {1}, {2, 3} and {4}.

A well-known fact concerning the adjacency matrix of a graph is that it

provides an easy method for counting the number of walks in a graph.

Theorem 7.13 Let A be the adjacency matrix of a graph G. Then the number

of walks from vertex i to vertex j of length k in G is given by the entry (A

)

of the matrix A

Example 7.14 For the adjacency matrices given in Example 7.8, the second

powers are given by

)

⎡

⎢

⎣

1011

0311

1121

1112

⎤

⎥

⎦

, (A

)

⎡

⎢

⎣

1012

0621

1222

2125

⎤

⎥

⎦

and (A

)

⎡

⎢

⎣

0011

0101

0011

0001

⎤

⎥

⎦

From these matrices, we can read oﬀ the number of walks of length two in the

graphs in Figure 7.1. For example, for the graphs G

and G

there are three

(closed) paths from 2 to 2,namely2 → 1 → 2, 2 → 3 → 2,and2 → 4 → 2.

Note that the multi-edge in graph G

increases the number of paths from 2 to

2 from three to six, since the multi-edges allow for diﬀerent ways to create the

path the 2 → 3 → 2. If we label the edges as e

and e

, then there are four

paths (described via the respective edges): e

, e

,ande

For the digraph G

there are overall fewer paths of length two, as direction

plays a role. However, paths in G

may involve the loop at vertex 4.For

250 Combinatorics of Compositions and Words

example, the path of length two from 2 to 4 involves going around the loop

once, 2→4→4.

Note that the k-th power of a matrix can be computed and displayed in

matrix format by using the following Mathematica and Maple commands:

MatrixPower[A,k]//MatrixForm

and

with(linalg):evalm(A^k)

respectively.

We need one more generalization of a graph in order to apply automata to

compositions.

Deﬁnition 7.15 An (edge)-weighted directed graph is a digraph in which

each edge of the graph has been assigned a weight.

By modifying the deﬁnition of the adjacency matrix, we can obtain a result

similar to Theorem 7.13 for these more general graphs.

Deﬁnition 7.16 For a weighted graph G with n vertices, we deﬁne the

weighted adjacency matrix as A =(a

)

n×n

where a

is the sum of the

weights of all edges from vertex i to j. For a walk P = i

···i

with edges

=(i

j+1

) and associated weights c

, the weight of the walk c(P ) is de-

ﬁned as the product of the edge weights of all the edges of the walk, that is,

c(P )=



k−1

j=0

Note that Deﬁnition 7.16 reduces to Deﬁnition 7.7 by assigning a weight of

one to every edge of a nonweighted graph.



•

acb

FIGURE 7.3: An edge-weighted directed graph.

Example 7.17 Figure 7.3 shows an example of a weighted digraph. Edges

(1, 2), (1, 4) and (2, 4) have weight a, the second (1, 2) edge has weight c,and

Automata and Generating Trees 251

the two remaining edges have weight b. The weighted adjacency matrix for

this graph is given by

⎡

⎢

⎣

0 a + c 0 a

00ba

000b

0000

⎤

⎥

⎦

The weight of the path P =1→ 2 → 4 is either given by c(P )=ca or

c(P )=a

, depending on which of the (1, 2) edges is chosen.

With this deﬁnition of the weight of a walk and the weighted adjacency

matrix, we have the following generalization of Theorem 7.13.

Theorem 7.18 Let A be the adjacency matrix of a weighted directed graph

G. Then the total weight of all walks from vertex i to vertex j of length k in

G is given by the entry (A

)

of the matrix A

Example 7.19 For the adjacency matrix A

deﬁned in Example 7.17, the

second power is given by

)

⎡

⎢

⎣

00b(a + c) a(a + c)

00 0 b

00 0 0

⎤

⎥

⎦

The rows consisting of zeros indicate that there are no walks from either vertex

3 or vertex 4 to anywhere in two steps. (In fact, there will be no walks to

anywhere from vertices 3 or 4 in k steps with k ≥ 2). The total weight of

walks from vertex 1 to vertex 4 is given by a(a + c), accounting for the two

paths with weights a

and ca.

Now we look at a special type of graph that we will need in Section 7.4

when discussing generating trees.

Deﬁnition 7.20 A tree T of order n is a simple, connected, acyclic graph on

n vertices. A vertex of a tree with degree one is called a leaf. A tree is called a

rooted tree if one vertex has been designated the root, in which case the edges

have a natural orientation away from the root. The tree order is the partial

ordering on the vertices of a tree with u ≤ v if and only if the unique path

from the root to v passes through u. If there is a directed edge from vertex i

to j,thenj is called the child of i,andi is called the parent of j.Theheight

or level of a vertex in a rooted tree is the length of the path from the root to

the vertex. A labeled tree is a tree in which each vertex is labeled.

Trees can be classiﬁed in many diﬀerent ways.

252 Combinatorics of Compositions and Words

Theorem 7.21 The following statements are equivalent for a tree T :

1. T is a tree.

2. There is a unique path in T between any two vertices in T .

3. Removing any edge from T results in a disconnected graph.

4. Addition of any edge between two nonadjacent vertices in T results in a

cycle.

Example 7.22 Figure 7.4 shows three trees. Tree T

has order eight, while

the labeled trees T

and T

both have order six. Looking at T

, we can identify

three leafs, namely vertices 3, 5 and 6. If we designate vertex 1 as the root,

then the height of the leaf 5 is 3 and the height of vertex 4 is 2.

•



•



•



•



•



•



•

FIGURE 7.4: A sampling of trees.

Note that the vertex labels of a tree of order n often consist of the numbers

1, 2,...,n to uniquely identify each vertex of the tree, but can also consist

of labels that identify what the vertex is representing (for example in a ge-

nealogical tree), or a property that the vertex has. Tree T

is an example of

the type of labeling we will be using for the generating trees in Section 7.4.

7.3 Automata

An automaton is a mathematical model for a ﬁnite state machine, which

starts in an initial state and then is fed one input symbol at a time. It has an

associated transition function (encoded for example in a look-up table) that

tells the machine to which state to move based on the current state and the

input read. Once the input stream is depleted, the automaton stops in either

Automata and Generating Trees 253

an accept or a reject state. Depending on the state in which the automaton

stops, it either accepts or rejects the input stream (or word). The set of words

accepted by an automaton is called the language accepted by the automaton.

We will use automata to enumerate words and compositions that avoid a

given pattern. To do so, we will ﬁrst deﬁne a general automaton, and then

specify the components for the automaton that enumerates the number of

words avoiding a speciﬁc pattern. Expressing the enumeration problem in

terms of an automaton is useful when investigating a speciﬁc pattern (as each

pattern has a tailored automaton), but does not work well for discovering

results for families of patterns. One exception is the family of increasing

patterns τ



=12···( + 1), for which we will obtain structural results that

allow us to compute the asymptotic behavior of AW



[k]

Deﬁnition 7.23 A ﬁnite automaton is given by

A =(E, Σ, Δ,S

,F),

where

•E= {S

,...,S

} is a ﬁnite set of states;

• Σ is a ﬁnite set of symbols {Σ

, Σ

,...,Σ



} called the alphabet of the

automaton;

• Δ is the transition function, that is, Δ:E×Σ

∗

→E,whereΣ

∗

the set of all ﬁnite words w = w

···w

such that w

∈ Σ for all

i =1, 2,...,m;

• S

= ε is the initial state of the automaton before any input has been

processed; and

• F is a subset of E, called the accept states.

We identify the automaton A with a directed graph in which the ver-

tex labels denote (the equivalence classes of) the states S

,...,S

.If

Δ(S

, Σ

)=S

, then the edge from S

to S

is labeled Σ

. The adjacency

matrix of this graph can then be used to count the number of walks of any

length from state S

to S

. Note that the edge labels do not signify weights

unless stated otherwise.

Example 7.24 We will deﬁne an automaton to count the number of tilings

of size 2 × n with squares and dominos (see Example 3.18) that cannot be

vertically split into two smaller tilings of sizes 2 ×n

and 2 ×(n −n

).These

types of tilings have been referred to as basic blocks [84] or indecomposable

blocks [30]. We denote the empty tiling by ε. In order to produce proper

tilings, we have to put any new tile into the leftmost possible position without

creating empty spots to the left of an occupied spot. The choices for placement

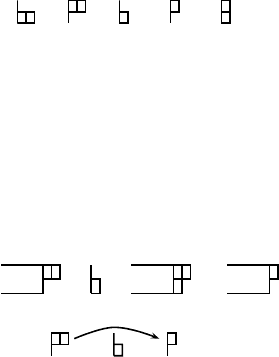
254 Combinatorics of Compositions and Words

of a tile are: placing either a square or a domino in the top row or in the

bottom row, or placing a domino vertically. The latter choice is allowed only

at the left end of the tiling (anywhere else, it would produce a place where the

tiling can be split). These choices constitute our alphabet, and we depict them

Next we need to identify the states of the automaton. Placing a tile changes

the shape of the right edge, and furthermore, the shape of the right edge allows

us to detect when we have completed a tiling (when we have reached a straight

right edge). Thus, the states constitute the equivalence classes of all tilings that

have a particular shape of the right edge (as we do not care about the particular

tiling, just the shape of the right edge). Figure 7.5 shows how placement of

a tile changes the tiling, and how this is expressed in the associated graph in

terms of the respective states.

+ = →

 

FIGURE 7.5: Example of transition function for tilings.

Now we are ready for drawing the graph of the tiling automaton. If the au-

tomaton is in the initial state, then we are allowed any of the ﬁve possible

placements described above. The set of ﬁnal states consists of only the verti-

cal domino (this is the one that we are interested in – being in this state is

equivalent to having completed a basic block). For any other state, the only

choices we have are to place a square or a horizontal domino into the other

row. Figure 7.6 shows the automaton graph G

for the tiling problem.

After having warmed up with the visual example of tilings, we now focus

on automata for pattern avoidance.

7.3.1 Automata and pattern avoidance in words

We will deﬁne an automaton to count the number of words avoiding a

certain subsequence pattern (see Deﬁnition 5.2). As we have seen in Exam-

ple 7.24, the states of the automaton correspond to equivalence classes that

lump together combinatorial objects that are equivalent with regard to the

characteristic that we want to enumerate. Here we are interested in pattern

avoidance, so sequences that have the same structure with regard to avoidance

of the given pattern should be equivalent. Speciﬁcally, two sequences (words