Heubach S., Mansour T. Combinatorics of Compositions and Words
Подождите немного. Документ загружается.


Words 235
Exercise 6.7 Prove that the polynomials U
j
(q) in Table 6.1 given for the
pattern 123 satisfy
U
n
(0) =
1
2
%
(−1)
n/3
+(−1)
(n+1)/3
&
.
Exercise 6.8 Use the scanning-element algorithm to obtain that the gener-
ating function for words avoiding the pair of subsequence patterns {132, 122}
is given by
AW
{132,122}
(x, y)=
(1 − x)(1 −y) −
:
(1 + y − x + xy)
2
− 4y
2x(1 − y)
.
Exercise 6.9
∗
Prove that the generating function for the number of k-ary
smooth words of length n (seeExercise2.17) is given by
1+
x(k − (3k +2)x)
(1 − 3x)
2
+
2x
2
(1 − 3x)
2
1+U
k−1
1−x
2x
U
k
1−x
2x
,
where U
s
is the s-th Chebyshev polynomial of the second kind (see Definition
C.1 ). Then show that the number of k-ary smooth words of length n is given
by
1
k +1
k
j=1
(1 + (−1)
j+1
)cot
2
%
jπ
2(k +1)
&%
1+2cos
%
jπ
k +1
&&
n−1
.
Exercise 6.10
∗
A k-ary word w = w
1
w
2
···w
n
is said to be smooth cyclic
if the word w
1
w
2
···w
n
w
1
is smooth. Prove that generating function for the
number of k-ary smooth cyclic words of length n is given by
1+
kx(1 + 3x)
(1 + x)(1 − 3x)
−
2(k +1)x
(1 + x)(1 − 3x)
U
k−1
1−x
2x
U
k
1−x
2x
,
where U
s
is the s-th Chebyshev polynomial of the second kind (see Definition
C.1 ). Then show that the number of k-ary smooth words of length n is given
by
k
j=1
"
1+2cos
%
jπ
k +1
&
#
n
.
Exercise 6.11 A (set) partition of [n] is a collection B
1
,...,B
d
of nonempty
disjoint sets, called blocks, whose union is the set [n]. Wewillassumethat
B
1
,B
2
,...,B
d
are listed in increasing order of their minimal elements. To
each partition we associate its canonical sequence, which is an integer se-
quence w = w
1
w
2
···w
n
such that w
i
= k if and only if i ∈ B
k
. For instance,
© 2010 by Taylor and Francis Group, LLC

236 Combinatorics of Compositions and Words
the partition of [7] into the four blocks {1, 4}, {2, 5, 7}, {3},and{6} has as-
sociated canonical sequence 1231242. We will refer to the canonical sequence
of a set partition of n as a partition word of length n.
Note that a word w on [d] represents a set partition with d blocks if and
only if it has the following properties:
(1) Each letter from the set [d] appears at least once in w.
(2) For each i, j such that 1 ≤ i<j≤ d, the first occurrence of i precedes
the first occurrence of j.
We remark that sequences satisfying these properties are also known as re-
stricted growth functions and they are often encountered in the study of set
partitions and related topics (see [175, 190] and references therein).LetP
n
de-
note the set of partition words of length n.ThenP
1
= {1}, P
2
= {11, 12} and
P
3
= {111, 112, 121, 122, 123}. Prove that the exponential generating function
for the number of partition words of length n is given by e
e
x
−1
.
Exercise 6.12
∗∗
Using the definitions of Exercise 6.11, determine
(1) the generating functions for the number of partition words of size n that
avoid a single pattern from the set P
3
= {111, 112, 121, 122, 123},and
(2) the generating functions for the number of partition words of size n that
avoid a single pattern from the set P
4
= {1111, 1112, 1121, 1122, 1123,
1211, 1212, 1213, 1221, 1222, 1223, 1231, 1232, 1233, 1234}.
Note that a complete classification with regard to Wilf-equivalence for avoid-
ance of partition word patterns in partition words has been given up to n =7
in [104].
Exercise 6.13
∗
Combining the definitions in Exercises 6.9 and 6.11, prove
that the generating function for the number of smooth partition words of [n]
is given by
1+
x
1 − 3x
⎛
⎝
1 −
k≥1
1
U
k
1−x
2x
U
k−1
1−x
2x
⎞
⎠
,
where U
s
is the s-th Chebyshev polynomial of the second kind. Then, show
that the number of smooth partition words of [n] with k blocks is given by
2
k +1
k
j=1
(1 + (−1)
j+1
)cos
2
%
jπ
2(k +1)
&
1+2cos
%
jπ
k +1
&
n−1
−
2
k
k−1
j=1
(1 + (−1)
j+1
)cos
2
%
jπ
2k
&
1+2cos
%
jπ
k
&
n−1
.
© 2010 by Taylor and Francis Group, LLC

Words 237
6.9 Research directions and open problems
We now suggest several research directions, which are motivated both by
the results and exercises of this chapter. In later chapters we will revisit some
of these research directions and pose additional questions.
Research Direction 6.1 Let r
k
be the number of Wilf-equivalence classes
for pattern avoidance of k-letter subsequence patterns in words. Clearly, t
1
=1
and t
2
=2, and Tables 6.2 through 6.5 show that r
3
=3, r
4
=4, r
5
=12and
r
6
=71. Any nontrivial information on r
n
is of interest!
Research Direction 6.2 We have obtained explicit formulas for the gener-
ating functions for the number of k-ary words of length n that avoid a subse-
quence pattern of length three (see Table 6.2 for the Wilf-equivalence classes
and Theorems 6.21, 6.23 and 6.25 for the generating functions).Anatural
extension is to find explicit formulas for the generating functions for the num-
ber of k-ary words of length n that avoid a subsequence pattern of length four.
Table 6.3 shows that there are four Wilf-equivalence classes, represented by the
patterns 1223, 1234, 1123 and 1112. Burstein and Mansour [33] have already
derived the generating function for the number of k-ary words of length n that
avoid the subsequence pattern 1112, but finding the generating functions for
the other three classes remains an open problem.
Research Direction 6.3 Table 6.3 gives the full classification of Wilf-equiv-
alence classes for subsequence patterns (that is, patterns of type (1, 1, 1, 1))
for k-ary words. This leads to the larger question of classifying the Wilf-
equivalence classes for the remaining (generalized) patterns of length four,
namely subword patterns of length four and generalized patterns of type (3, 1),
(2, 2), (1, 2, 1),and(2, 1, 1). Using a computer program, we have obtained
the sequences of the number of 5-ary words of length n for n =1,...9 for
the various patterns of length four. These sequences are listed in Tables 6.6
through 6.10 at the end of this section.
(1) Table 6.6 conjectures that for subword patterns
– 1221 ∼ 1121,
– 1223 ∼ 1213,
– 1423 ∼ 1243,
– 1432 ∼ 1342,
– 2143 ∼ 1324,
– 1132 ∼ 1232 ∼ 1322 ∼ 1332.
© 2010 by Taylor and Francis Group, LLC
238 Combinatorics of Compositions and Words
To obtain the complete classification for the Wilf-equivalence classes for
subword patterns of length four in k-ary words, prove or disprove each
of the above Wilf-equivalences. That is, either compute additional values
to show that the equivalence is not true, or give a proof that the patterns
are indeed equivalent.
(2) Table 6.7 conjectures that for type (3, 1) patterns
– 132–2 ∼ 132–1,
– 213–2 ∼ 213–1,
– 133–2 ∼ 113–2,
– 123–4 ∼ 234–1,
– 112–1 ∼ 122–1 ∼ 122–2,
– 123–1 ∼ 123–2 ∼ 123–3,
– 121–3 ∼ 212–3 ∼ 131–2,
– 122–3 ∼ 112–3 ∼ 211–3 ∼ 221–3,
– 124–3 ∼ 134–2 ∼ 214–3 ∼ 143–2,
– 213–4 ∼ 132–4 ∼ 142–3 ∼ 231–4 ∼ 241–3 ∼ 243–1.
T
o obtain the complete classification for the Wilf-equivalence classes for
patterns of type (3, 1) in k-ary words, prove or disprove each of the above
Wilf-equivalences.
(3) Table 6.8 conjectures that for type (2, 2) patterns
– 12–13 ∼ 13–12,
– 12–23 ∼ 12–32 ∼ 21–32,
– 11–21 ∼ 11–12,
– 11–23 ∼ 11–32,
– 13–24 ∼ 24–13,
– 12–43 ∼ 21–43 ∼ 12–34.
T
o obtain the complete classification for the Wilf-equivalence classes of
patterns of type (2, 2) in k-ary words, prove or disprove each of the above
Wilf-equivalences.
(4) Table 6.9 conjectures that for type (1, 2, 1) patterns
– 1–12–2 ∼ 1–21–2,
– 1–31–2 ∼ 1–13–2,
– 1–33–2 ∼ 1–22–3,
– 2–14–3 ∼ 2–41–3,
© 2010 by Taylor and Francis Group, LLC
Words 239
– 1–42–3 ∼ 1–24–3,
– 1–23–2 ∼ 1–21–3 ∼ 1–32–2 ∼ 1–12–3,
– 1–43–2 ∼ 1–23–4 ∼ 1–34–2 ∼ 1–32–4.
To obtain the complete classification for the Wilf-equivalence classes of
patterns of type (1, 2, 1) in k-ary words, prove or disprove each of the
above Wilf-equivalences.
(5) Table 6.10 conjectures that for type (2, 1, 1) patterns
– 12–1–2 ∼ 12–2–1,
– 11–1–2 ∼ 11–2–1,
– 21–3–1 ∼ 21–1–3,
– 11–3–2 ∼ 11–2–3,
– 12–3–1 ∼ 12–1–3,
– 13–3–2 ∼ 13–2–3,
– 12–1–1 ∼ 12–2–2,
– 21–3–3 ∼ 12–3–3,
– 23–1–4 ∼ 23–4–1,
– 13–2–4 ∼ 13–4–2,
– 21–2–3 ∼ 12–3–2 ∼ 21–3–2 ∼ 12–2–3,
– 12–4–3 ∼ 21–3–4 ∼ 21–4–3 ∼ 12–3–4.
T
o obtain the complete classification for the Wilf-equivalence classes of
patterns of type (2, 1, 1) in k-ary words, prove or disprove each of the
above Wilf-equivalences.
Research Direction 6.4 In Exercise 6.9 we obtained explicit formulas for
the number of smooth k-ary words of length n. More generally, a word w =
w
1
···w
n
is said to be -smooth if |w
i
− w
i+1
|≤, for all i =1, 2,...,n− 1.
Clearly, a 1-smooth word is a smooth word. Find an explicit formula for the
number of -smooth k-ary words of length n.
Research Direction 6.5 In Exercise 6.10 we obtained explicit formulas for
the number of smooth cyclic k-ary words of length n. More generally, a word
w = w
1
···w
n
is said to be -smooth cyclic if w
1
···w
n
w
1
is an -smooth
word. Clearly, a 1-smooth cyclic word is a smooth cyclic word. Find an
explicit formula for the number of -smooth cyclic k-ary words of length n.
© 2010 by Taylor and Francis Group, LLC

240 Combinatorics of Compositions and Words
TABLE 6.6: {AW
τ
5
(n)
9
n=1
} for 4-letter subword patterns τ
τ {AW
τ
5
(n)}
9
n=1
for 4-letter subword patterns τ
1123 5 25 125 615 3025
14875 73126 359485 1767200
1112 5 25 125 615 3025
14875 73135 359575 1767875
1132, 1232 5 25 125 615 3025
1322, 1332
14875 73138 359605 1768100
1221, 1121 5 25 125 615 3025
14875 73155 359775 1769375
1223, 1213 5 25 125 615 3025
14880 73176 359859 1769690
1231 5 25 125 615 3025
14875 73171 359935 1770575
1312 5 25 125 615 3025
14880 73188 359979 1770576
2132 5 25 125 615 3025
14880 73209 360189 1772131
1212 5 25 125 615 3025
14885 73235 360315 1772755
1122 5 25 125 615 3025
14885 73235 360320 1772815
1423, 1243 5 25 125 620 3075
15250 75625 375025 1859750
1432, 1342 5 25 125 620 3075
15250 75628 375055 1859975
2143, 1324 5 25 125 620 3075
15251 75635 375100 1860250
2413 5 25 125 620 3075
15251 75639 375140 1860546
1234 5 25 125 620 3076
15260 75700 375525 1862865
1111 5 25 125 620 3080
15300 76000 377520 1875280
TABLE 6.7: {AW
τ
5
(n)
9
n=1
} for 4-letter patterns τ of type (3, 1)
τ {AW
τ
5
(n)}
9
n=1
for 4-letter patterns τ of type (3, 1)
112–1, 122–1 5 25 125 615 2985
122–2
14315 67945 319695 1493355
213–3 5 25 125 615 2985
14315 67971 320117 1497634
132–2, 132–1 5 25 125 615 2985
14315 67971 320117 1497638
© 2010 by Taylor and Francis Group, LLC

Words 241
τ {AW
τ
5
(n)}
9
n=1
for 4-letter patterns τ of type (3, 1)
112–2 5 25 125 615 2985
14325 68065 320660 1499795
213–2, 213–1 5 25 125 615 2985
14320 68031 320601 1500861
132–3 5 25 125 615 2985
14325 68091 321081 1504044
121–2 5 25 125 615 2985
14325 68105 321335 1506885
123–1, 123–2 5 25 125 615 2985
123–3
14325 68117 321508 1508438
121–1 5 25 125 615 2985
14345 68345 323185 1518765
133–2, 113–2 5 25 125 615 2995
14479 69639 333697 1594632
122–3, 112–3 5 25 125 615 2995
211–3, 221–3
14484 69705 334283 1598959
121–3, 212–3 5 25 125 615 2995
131–2
14499 69903 336005 1611495
111–2 5 25 125 615 3015
14745 71999 351216 1712064
124–3, 134–2 5 25 125 620 3057
214–3, 143–2
15004 73386 357984 1742678
213–4, 132–4 5 25 125 620 3057
142–3, 231–4
15006 73414 358246 1744710
241–3, 243–1
123–4, 234–1 5 25 125 620 3058
15018 73517 359000 1749747
111–1 5 25 125 620 3060
15040 73660 359720 1752600
TABLE 6.8: {AW
τ
5
(n)
9
n=1
} for 4-letter patterns τ of type (2, 2)
τ {AW
τ
5
(n)}
9
n=1
for 4-letter patterns τ of type (2, 2)
12–12 5 25 125 615 2975
14155 66235 304690 1377400
12–21 5 25 125 615 2975
14155 66255 305130 1382900
12–13, 13–12 5 25 125 615 2975
14165 66467 307743 1407523
13–32 5 25 125 615 2975
14165 66467 307748 1407638
12–31 5 25 125 615 2975
14170 66542 308442 1412766
© 2010 by Taylor and Francis Group, LLC

242 Combinatorics of Compositions and Words
τ {AW
τ
5
(n)}
9
n=1
for 4-letter patterns τ of type (2, 2)
12–23, 12–32 5 25 125 615 2975
21–32
14175 66643 309636 1423624
11–21, 11–12 5 25 125 615 2985
14305 67765 317675 1475345
13–22 5 25 125 615 2985
14319 68005 320227 1496892
11–23, 11–32 5 25 125 615 2990
14400 68824 326871 1544221
11–22 5 25 125 615 2995
14455 69235 329430 1558430
13–42 5 25 125 620 3050
14893 72239 348300 1670218
13–24, 24–13 5 25 125 620 3050
14894 72258 348521 1672241
14–23 5 25 125 620 3051
14910 72420 349850 1681880
14–32 5 25 125 620 3051
14911 72437 350030 1683410
12–43, 21–43 5 25 125 620 3052
12–34
14927 72601 351401 1693579
11–11 5 25 125 620 3060
15020 73340 356280 1722200
TABLE 6.9: {AW
τ
5
(n)
9
n=1
} for 4-letter patterns τ of type (1, 2, 1)
τ {AW
τ
5
(n)}
9
n=1
for 4-letter patterns τ of type (1, 2, 1)
1–12–2, 1–21–2 5 25 125 615 2945
13615 60385 255670 1029655
1–12–1 5 25 125 615 2945
13625 60555 257365 1042325
2–13–2 5 25 125 615 2945
13659 61301 266545 1125450
1–23–1 5 25 125 615 2950
13750 62270 274431 1179730
1–31–2, 1–13–2 5 25 125 615 2955
13819 62824 277717 1195051
1–23–2, 1–21–3 5 25 125 615 2955
1–32–2, 1–12–3
13834 63116 281025 1223497
1–22–1 5 25 125 615 2955
13835 63195 282545 1241645
1–11–2 5 25 125 615 2975
14145 66159 304797 1385315
1–33–2, 1–22–3 5 25 125 615 2975
14169 66593 309565 1426269
© 2010 by Taylor and Francis Group, LLC

Words 243
τ {AW
τ
5
(n)}
9
n=1
for 4-letter patterns τ of type (1, 2, 1)
1–11–1 5 25 125 620 3040
14700 69980 327620 1507580
2–14–3, 2–41–3 5 25 125 620 3039
14704 70240 331523 1547611
1–42–3, 1–24–3 5 25 125 620 3039
14705 70262 331803 1550313
1–43–2, 1–23–4 5 25 125 620 3040
1–34–2, 1–32–4
14723 70459 333500 1562970
TABLE 6.10: {AW
τ
5
(n)
9
n=1
} for 4-letter patterns τ of type (2, 1, 1)
τ {AW
τ
5
(n)}
9
n=1
for 4-letter patterns τ of type (2, 1, 1)
12–1–2, 12–2–1 5 25 125 615 2945
13615 60405 256100 1034890
11–1–2, 11–2–1 5 25 125 615 2945
13625 60555 257365 1042325
22–1–3 5 25 125 615 2945
13659 61301 266545 1125450
21–3–1, 21–1–3 5 25 125 615 2955
13819 62814 277513 1192670
11–3–2, 11–2–3 5 25 125 615 2950
13760 62460 276491 1196542
12–3–1, 12–1–3 5 25 125 615 2955
13824 62920 278786 1204052
13–1–2 5 25 125 615 2955
13829 63025 280051 1215519
13–2–1 5 25 125 615 2955
13834 63110 280904 1222093
21–2–3, 12–3–2 5 25 125 615 2955
21–3–2, 12–2–3
13834 63116 281025 1223497
13–3–2, 13–2–3 5 25 125 615 2955
13834 63128 281267 1226285
11–2–2 5 25 125 615 2955
13855 63595 286975 1277865
12–1–1, 12–2–2 5 25 125 615 2975
14145 66159 304797 1385315
13–2–2 5 25 125 615 2975
14169 66593 309565 1426269
21–3–3, 12–3–3 5 25 125 615 2975
14175 66697 310650 1435091
11–1–1 5 25 125 620 3040
14700 69980 327620 1507580
© 2010 by Taylor and Francis Group, LLC
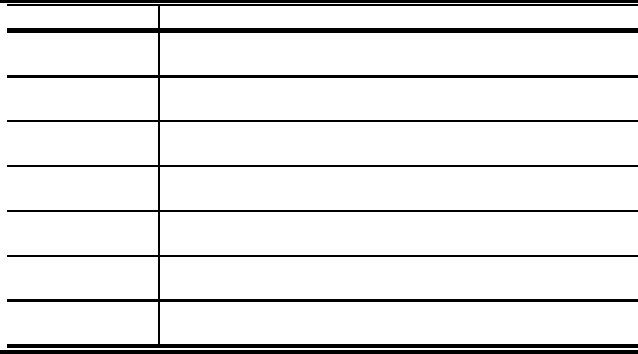
244 Combinatorics of Compositions and Words
τ {AW
τ
5
(n)}
9
n=1
for 4-letter patterns τ of type (2, 1, 1)
24–3–1 5 25 125 620 3039
14703 70223 331354 1546331
24–1–3 5 25 125 620 3039
14704 70241 331546 1547914
23–1–4, 23–4–1 5 25 125 620 3039
14705 70261 331781 1550034
13–2–4, 13–4–2 5 25 125 620 3039
14705 70262 331803 1550313
14–2–3 5 25 125 620 3040
14723 70459 333499 1562946
14–3–2 5 25 125 620 3040
14724 70477 333692 1564552
12–4–3, 21–3–4 5 25 125 620 3040
21–4–3, 12–3–4
14724 70479 333736 1565112
© 2010 by Taylor and Francis Group, LLC
