Хермен Г. Восстановление изображений по проекциям: Основы реконструктивной томографии

Подождите немного. Документ загружается.

ГЛАВА

]

Рис. 1.17. Система эмиссионной реконструктивной томографии Лаборатории Дон-

нер,

в которой используется 280 шинтилляционных детекторов, размещенных во-

круг пациента.

Экспериментальные данные, необходимые

для

оценки ленейных интегралов распределения

ра-

диоактивности

пациенте, одновременно снимаются для 240 проекций

по

105 линий

каждой.

(Иллюстрация предоставлена д-ром

Т. Ф.

Балннгером.)

размножителей на быстрых нейтронах, которые находятся внутри сталь-

ных связок, допускающих проверку. На рис^19, а показана топливная связ-

ка с 91 тепловыделяющим элементом, которая помещена в стальной гекса-

гональный канал, не показанный на рисунке. В этом узле находятся три

контрольных элемента, которые в сечении при реконструкции изображения

должны давать пустые места. (Именно этот дефект мы ищем). Типичный

снимок этого топливного узла, получаемый с помощью нейтронов, показан

на рис. 1.19, б, Изображение сечения, восстановленное по 20 таким сним-

кам топливного узла, приведено на рис. 1.19, е.

Примером использования метода восстановления по проекциям, когда

«объект», изображение которого необходимо реконструировать, имеет раз-

меры порядка сантиметров, является задача определения трехмерных па-

лей температур при помощи голографической интерферометрии. Опуская

описание этого метода, перейдем к объекту на микроскопическом уровне.

На рис 1.20, а представлена электронная микрограмма бактериофага. Дли-

на черной полосы внизу рисунка соответствует 1000 А (10~

м). На

рис. 1.20, б в области, ограниченной прямоугольником, часть отростка по-

казана с еще большим увеличением. На рис. 1.20, в видна дифракционная

ВВЕДЕНИЕ

Эммисионная

Схема полушении трансмиссионной

томограмма

томограммы

Перед фшигеской При

физической

нагрузкой наг.ру$ке

Рис. 1.18. Иллюстрации, показывающие принцип действия системы, используемой в

Лаборатории Доннер для получения изображений ядер рубидия-82, накопленных в

миокарде человека.

Внизу слева показано трансмиссионное томографическое изображение миокарда и свода печени;

на двух снимках справа

—

распределение ядер рубидия, по которым можно судить о коронарном

потоке крови до и во время физической нагрузки. Отношение степени заполнения равно 1,7. (Ил-

люстрация предоставлена д-ром Т. Ф. Бадннгером.)

картина, создаваемая этой частью отростка. Модель строения этих объек-

тов,

полученная на основе оптического дифракционного анализа с низким

разрешением, показывает, что сам отросток составлен из частей толщиной

38 А с аксиальной вращательной симметрией третьего порядка в виде

стопки с углом скручивания 41,5°. Если предположить, что все эти сечения

идентичны, то одна-единственная электронная микрограмма создает доста-

точно большое число проекций и тем самым делает возможным восстанов-

ление трехмерного изображения. На рис. 1.20, г показано такое трехмерное

изображение, восстановленное по трем сечениям.

На этом закончим обзор некоторых применений метода восстановления

изображений по проекциям. За исключением некоторых аспектов рентге-

новской РТ, которые будут обсуждены ниже, остальная часть книги посвя

щена теоретическим основам, а не применениям метода восстановления

изображений по проекциям.

4i»

-т

Падающий пугок

нейтроноб

Фильтр из кадмия

Связка из 91

тепловыделяющего

-.^'l&^.tei&$i- "%*

элемента, сориентирован- . j$fr£^&■ %- '''

на*

под углом 10° к *

£*-."£

\.' "•*!-

'®«*Ч.

нейтронов £%£ *-".

*\ . = * *r^. i

Затемненные '&J*Wc '&.:

'■%*.*.'

•£•

rJ5>

*>&

элементы имеют

пустые секции

Фильтр из гадолиния

Фольга из индия

Экран из кадмия

***z*z*zk

vz#z*z%f

*2*2*i*Z*

Рис, 1.19. Нейтронная радиография топливной связки.

о — объект, изображение которого реконструируют; б — типичный нейтроиографический

сни-

мок; в — реконструкция по 20 таким

снимкам;

г — реконструкция по данным без шума (модели-

рование на ЭВМ). (Иллюстрации предоставлены д-ром Дж. П. Бартоном, фирма IRT (частное

сообщение 8 февраля 1979 г ))

ВВЕДЕНИЕ

Рис. 1.20. Реконструкция отростка бактериофага

Caulobacter crescentus

0CbK.

—

электронная микрограмма бактериофага

фСЪК

(негативно окрашенная

1%-ным

раствором

уранилацетата). Длина полосы соответствует 1000 А; б

—

отростки бактериофага

ФСЪК.

Пло-

щадь прямоугольника составляет 200 х 1000 А; в

—

дифракционная картина, производимая той

частью отростка фСЬК, которая находится в указанном прямоугольнике. Стрелки указывают

промежуток 1/38 А; г

—

реконструированное трехмерное изображение части отростка бактерио-

фага фСЬК, содержащее три аксиальных периодических повторений (114 А). Длина полосы соот-

ветствует 50 А. (Иллюстрация предоставлена д-рами С. Пападопулосом и П. Р. Смитом.)

1.2.ВЕРОЯТНОСТЬ И СЛУЧАЙНЫЕ ПЕРЕМЕННЫЕ

Чтобы обсуждать процессы, связанные с РТ, необходимо знать некото-

рые основные понятия теории вероятности. Цель этого раздела — оз-

накомить читателей с такими понятиями. При желании читатель может

бегло просмотреть данный материал и вернуться к нему позже, по мере

того как введенные здесь понятия будут использоваться в других разделах

книги.

ГЛАВА I

Истогник

Вакуум

у / /л

Слой /

вещества

Вакуум

Детектор

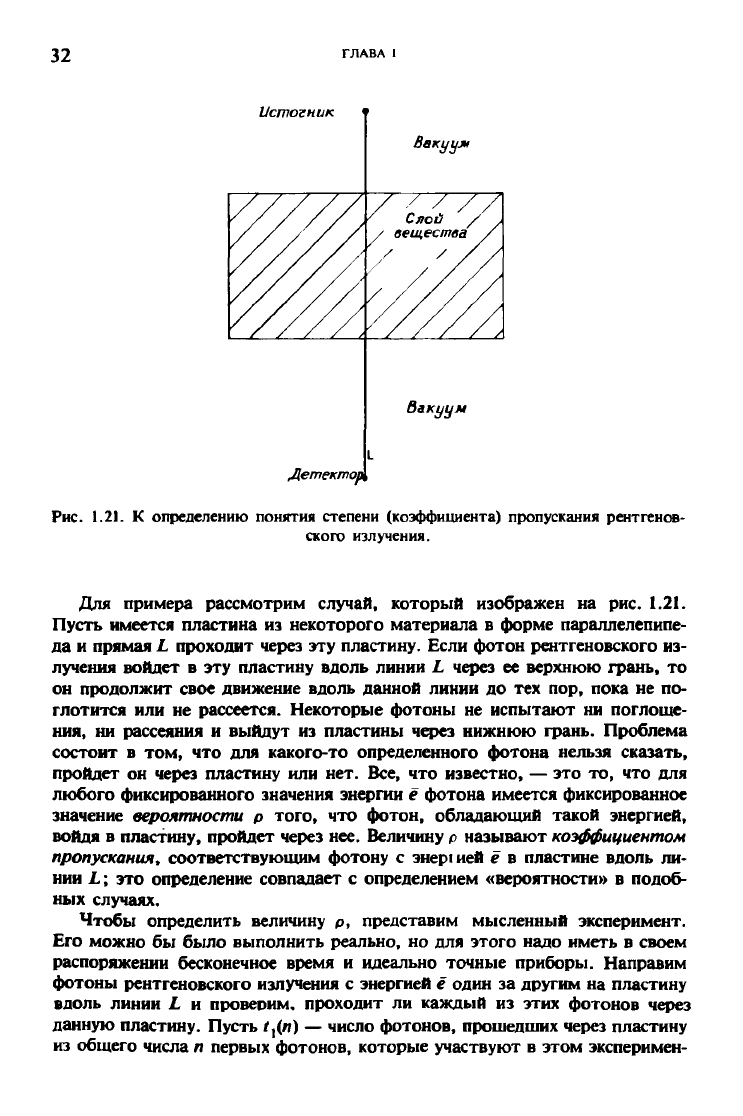
Рис. 1.21. К определению понятия степени (коэффициента) пропускания рентгенов-

ского излучения.

Для примера рассмотрим случай, который изображен на рис. 1.21.

Пусть имеется пластина из некоторого материала в форме параллелепипе-

да и прямая L проходит через эту пластину. Если фотон рентгеновского из-

лучения войдет в эту пластину вдоль линии L через ее верхнюю грань, то

он продолжит свое движение вдоль данной линии до тех пор, пока не по-

глотится или не рассеется. Некоторые фотоны не испытают ни поглоще-

ния,

ни рассеяния и выйдут из пластины через нижнюю грань. Проблема

состоит в том, что для какого-то определенного фотона нельзя сказать,

пройдет он через пластину или нет. Все, что известно, — это то, что для

любого фиксированного значения энергии ё фотона имеется фиксированное

значение вероятности р того, что фотон, обладающий такой энергией,

войдя в пластину, пройдет через нее. Величину р называют коэффициентом

пропускания* соответствующим фотону с

энер1

ией ё в пластине вдоль ли-

нии L; это определение совпадает с определением «вероятности» в подоб-

ных случаях.

Чтобы определить величину р, представим мысленный эксперимент.

Его можно бы было выполнить реально, но для этого надо иметь в своем

распоряжении бесконечное время и идеально точные приборы. Направим

фотоны рентгеновского излучения с энергией ё один за другим на пластину

вдоль линии L и проверим, проходит ли каждый из этих фотонов через

данную пластину. Пусть t

(n) — число фотонов, прошедших через пластину

из общего числа п первых фотонов, которые участвуют в этом эксперимен-

ВВЕДЕНИЕ

те.

(Индекс

указывает

на то, что

данный эксперимент является первым

таким мысленным экспериментом.

дальнейшем будет рассмотрена серия

подобных экспериментов.) Тогда величина

определяется

как

предел

/,(л)/л

при п - оо, т.е.

р= lim(r,(n)/n).

(1.1)

«-•со

Таким образом коэффициент пропускания

есть такое число,

что для лю-

бого данного положительного вещественного числа

£, как бы

мало

оно ни

было,

всегда найдется целое число

такое,

что

разность между

р и

(ji\/n меньше

е для

всех

л,

больших

Отметим»

что

заранее

ие

очевидно, имеет

ли

(n)/n предел при

—

оо.

Утвердительный ответ основан

на

реальных физических экспериментах,

ко-

торые являются приближением описанного выше мысленного эксперимен-

та.

Отметим также,

что мы

исходим

из

предположения,

что то же

самое

значение

будет получено, если такой опыт выполнить снова.

именно

пусть такой

же

мысленный опыт будет выполнен второй

раз и

пусть

tM) обозначает количество фотонов, прошедших через пластину

из

первых

п фотонов

во

втором опыте. Тогда

—

lim

(n)/n).

п — ов

Даже если величины

р,

определяемые как пределы,

этих двух идентич-

ных мысленных экспериментах одинаковы,

то это не

означает,

что

можно

принять

/,(л) = t

(n) для

любого фиксированного значения

п.

Любая

из ве-

личин

}

(n) и t

(n)

может принимать любое целое значение

от

нуля

(от-

сутствуют фотоны, прошедшие через пластину)

до п

(все фотоны проходят

через пластину). Однако некоторые

из

этих величин являются более веро-

ятными,

чем

другие. Разумно спросить: какова вероятность

(т)

того,

что

фотонов

из л,

вошедших

пластину, пройдут через нее?

Чтобы определить величину

(т),

выполним многократно описанный

выше мысленный эксперимент, пока

фотонов

не

войдут

пластину.

Пусть

—

число фотонов, прошедших через пластину

в /-м

подобном экс-

перименте,

s(/V)

—

число раз, когда /,(л)

= т для 1 < / < N.

Тогда опре-

делим

(т)=

lim(s(N)/N). (1.2)

N-oo

Заметим, что

(т) = 0,

если

т <

или

т > л. Так

как

(т) по

пред-

положению равно вероятности того,

что т

фотонов

из л

пройдут через

пластину,

то это

утверждение является разумным. Легко также видеть

из

сравнения мысленных экспериментов, использованных

для

определения

р и

РпУ™)*

что /Jj(l)

= р.

Несколько труднее показать,

что в

общем случае

для

т < п

ГЛАВА 1

[ml равно произведению

т (т

—

\){т -

2)...2-1,

а О! = 1.]

Выражение

(1.3) называют биномиальным вероятностным законом.

Множество всех возможных исходов эксперимента, подобного только

что рассмотренному, вместе

вероятностью каждого исхода называют

дискретной случайной переменной.

книге будут рассмотрены только

та-

кие эксперименты, исходы которых представляют собой число или вектор-

столбец чисел.

Например

для

фиксированных значений

множество целых чисел

вместе

вероятностью

(т)

называют биномиальной случайной перемен-

ной

параметрами

п и р.

Исходом единичного эксперимента назы-

вают выборку

или

отсчет случайной переменной. Например, величина

(п) для определенного значения

/ в

только

что

описанном мысленном экс-

перименте представляет собой выборку

из

биномиальной случайной пере-

менной

параметрами

п и ^.

Таким образом, число фотонов, которые могут пройти через материал

том

случае, когда

фотонов входят

пластину, является случайной пере-

менной. Реальное число фотонов, прошедших через пластину

единичном

эксперименте, является выборкой случайной переменной.

В дальнейшем

мы

познакомимся

другими случайными переменными.

Особенно важной величиной такого рода для наших целей является случай-

ная переменная, связанная

количеством фотонов, испущенных источни-

ком

направлении детектора

за

единицу времени.

Двумя наиболее важными характеристиками дискретных случайных

пе-

ременных являются среднее значение

дисперсия, которые определяются

следующим образом.

Пусть

— случайная переменная

набором возможных отсчетов

Для

х из 5

пусть

(х) —

вероятность того,

что

исход какого-то единично-

го эксперимента равен

х.

Тогда среднее значение

равно

Их = I *Рх(х\ (1.4)

а дисперсия

составит

Ух

= Т(* ~

Их)

Рх(х).

(1.5)

xeS

Отметим,

что

усредненное значение исхода при стремлении числа экспери-

ментов

очень большой величине приближается к среднему значению, при-

веденному выше.

свою очередь усредненное значение квадрата разности

между значением отсчета

средним значением

при

большом количестве

экспериментов стремится

дисперсии. Таким образом, дисперсия является

мерой разброса возможных исходов относительно среднего значения.

Для

переменной

биномиальным распределением

параметрами распределения

лир среднее значение равно

пр, а

дисперсия равна

пр(\ - р). По

определе-

нию среднеквадратичным отклонением случайной переменной называют

корень квадратный

из ее

дисперсии.

ВВЕДЕНИЕ

Будем говорить, что случайная переменная ведет себя как нормальная

переменная, если она обладает следующими свойствами: вероятность того,

что отсчет находится в пределах одного среднеквадратичного отклонения

от среднего значения, больше 0,65; вероятность того, что отсчет находится

в пределах двух среднеквадратичных отклонений от среднего значения,

больше 0,95; вероятность того, что отсчет находится в пределах трех сред-

неквадратичных отклонений от среднего значения, больше 0,995. Многие

случайные переменные, которые встречаются в РТ, ведут себя подобным

образом.

Важность понятия нормальной случайной переменной состоит в следую-

щем.

Часто требуется оценить среднее значение по одному или многим от-

счетам. В 95 случаях из 100 среднее значение нормальной случайной пере-

менной будет находиться в пределах двух среднеквадратичных* отклонений

от значения отсчета. Эквивалентным утверждением является следующее:

доверительность того, что среднее значение находится в пределах двух

квадратичных отклонений от значения отсчета, равна 95 %. Если мы обла-

даем методом оценки среднеквадратичного отклонения (а мы часто обла-

даем этим), тогда, имея результаты одной выборки, можно сказать, что

имеется 95%-ная доверительность того, что математическое ожидание на-

ходится от выборки в пределах от плюс до минус удвоенное среднеквадра-

тичное отклонение. Аналогично можно сказать, что имеется 99,5%-ная до-

верительность того, что математическое ожидание находится от выборки в

пределах от плюс до минус три среднеквадратичных отклонения. Можно

показать, что при условии, когда лр(1

—

р) велико (больше 10), биноми-

альное распределение ведет себя как нормальное.

Наконец, мы рассмотрим функции случайных переменных. В РТ неод-

нократно встречаются функции, аргументами которых являются выборки

случайных переменных. Например, число фотонов, зарегистрированных

счетчиком за время измерения, является случайной величиной, которую мы

обозначим буквой D. Чтобы исключить вариации интенсивности источника

рентгеновского излучения, число фотонов, зарегистрированных детекто-

ром,

обычно делят на число фотонов эталонного, или опорного, детекто-

ра,

которое также является выборкой случайной переменной R. Множество

всех исходов сложного эксперимента по счету фотонов детектором, счету

фотонов контрольным детектором и отношения первого числа ко второму

образует случайную переменную N. Предположим, что число фотонов, со-

считанных любым детектором, положительно. Пусть p

(x) и p

{x) — ве-

роятности того, что х фотонов сосчитаны детектором и контрольным де-

тектором соответственно. Тогда возможные исходы сложного эксперимен-

та являются положительными рациональными числами, и вероятность

PN(Q)

того, что исход составного эксперимента есть

определяется выра-

жением

РЛЧ) = X РОМРЛУУ (1.6)

Х.У

<*/у) = 9

ГЛАВА 1

В этом случае говорят, что случайная величина N получается делением слу-

чайной переменной D на случайную переменную R, т.е. N = D/R.

Аналогично, если X — случайная переменная с множеством S возмож-

ных исходов, составляющих положительные числа, то Y = In

Л'

— случай-

ная переменная, для которой множество возможных исходов составляет

натуральные логарифмы элементов, причем для х в S получим

(\nx)

(х).

Другие понятия теории вероятности будут рассмотрены

по мере надобности.

ПРИМЕЧАНИЯ И ССЫЛКИ

Книга, посвященная преимущественно применениям методов восстановления

изображений по проекциям, была издана под редакцией Хермена [67]. Она содержит

обзорные статьи по использованию методов реконструкции изображений для реше-

ния вопросов, связанных с внутренней структурой короны Солнца, распределением

яркости неба в радиодиапазоне и распределением радионуклидов как индикаторов

физиологического функционирования различных органов человека и динамической

работы его сердца. Вопросы, связанные с применением этих методов, освещены в

трудах семинара Technical Digest of the Meeting on Image Processing for 2-D and 3-D

Reconstruction from Projections, который состоялся в Станфорде (шт. Калифорния,

США) в 1975 г. при поддержке Института по медицинской электронике при Стан-

фордском университете

Оптического общества США. Сравнительно недавно состо-

ялся другой подобный семинар по физике и инженерным вопросам в реконструиро-

вании

томографии—в

1979

г.

в Ньюпорт-Биче

(шт.

Калифорния,

США).

Труды этого

се-

минара были опубликованы в томе NS-26 журнала IEEE Transactions за 1979 г.

Описание метода лунных покрытий для восстановления двумерных распределе-

ний радиоисточников приведено в работе

[152].

Общие вопросы использования мето-

да восстановления изображений в радиоастрономии изложены в работе [16]. Рас-

смотренный нами пример по рентгеновскому излучению остатка сверхновой в со-

эвезднии Парусов взят из работы

[122].

Очень полный обзор по использованию метода восстановления изображений по

проекциям применительно к исследованию короны Солнца дан в работе [1].

Использование метода восстановления изображений по проекциям для оценки

пространственных распределений загрязнителей воздуха описано в статье

[150].

Проблемы обнаружения айсбергов (хотя и без использования метода реконструкций)

описаны в работе [22].

Первой публикацией в открытой литературе по аппаратуре, при помощи кото-

рой были показаны потенциальные возможности реконструктивной томографии в

медицине, была работа

[124].

Алгоритмом реконструкции изображений, используе-

мым в этой работе, был, по существу, алгоритм обратного проецирования (описан-

ный в гл. 7). Более точный неитерационный алгоритм с разложением в ряд (гл. 13)

был предложен Кормаком в статье [34], которая также была посвящена описанию

потенциальных возможностей реконструкции изображений в медицинской диагно-

стике. Другая работа, которую можно считать одной из первых подобных публика-

ций,

посвящена применениям РТ в медицине. Это — отчет Куля и Эдвардса [98].

Первый серийно выпускаемый рентгеновский РТ-сканер разработан Хаунсфидпом

[88,

89] и использован для сканирования головы. РТ-сканер для всего тела человека

описан в работе

[104].

Хаунсфилд и Кормак за свои основополагающие работы по

ВВЕДЕНИЕ

реконструктивной томографии были удостоены Нобелевской премии по физиологии

я медицине за 1979 г.

Большое число работ по развитию и использованию методов реконструкции

изображений по проекциям и их использованию в медицине можно найти в сборнике

статей

[136].

В него включены статьи по рентгеновской, протонной, ультразвуковой

и эмиссионной реконструктивной томографии. Обзор развития рентгеновской РТ с

высокими временными характеристиками дан в работе

[1S8].

Лаутербур [102] напи-

сал небольшую статью с обширной библиографией по использованию ядерного маг-

нитного резонанса для получения изображений в медицинских целях. Весьма обстоя-

тельный обзор по эмиссионной реконструктивной томографии содержится в работе

[25].

В ней имеется также информация о поглощении миокардом ядра рубидия-82.

Материал по нераэрушающему контролю тепловыделяющих элементов ядерно-

го реактора взят из работы [12].

Методы и экспериментальные данные по определению трехмерных температур-

ных полей с помощью топографической интерферометрии описаны в работе

[132].

Подробности методики, которая использовалась при получении рис. 1.20, а так-

же ссылки на некоторые более ранние работы по реконструкции изображений по

электронным микрофотографиям можно найти в работе

[146].

Дополнительные данные по теории вероятности и статистической теории мож-

но найти в книге Парцеиа

[126],

в которой приведены дополнительный материал и

ссылки на оригинальные работы в этой области.