Hawkes P.W., Spence J.C.H. (Eds.) Science of Microscopy. V.1 and 2

Подождите немного. Документ загружается.

878 M. Howells et al.

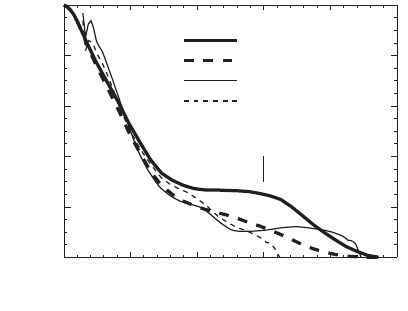
1992) in which the intensity point spread function and its Fourier

transform, the optical transfer function (OTF) were calculated. In fact,

the magnitude of the OTF, known as the modulation transfer function

(MTF), was both calculated and measured for the Stony Brook STXM

and good agreement was obtained (Figure 13–21). Similar analysis has

been provided for TXMs (Jochum and Meyer-Ilse, 1995; Niemann et al.,

2000). Jochum and Meyer-Ilse provided a fairly general treatment of

the application of coherence theory to X-ray microscopy including

imaging of two-point and step objects by a realistic TXM in bright-ﬁ eld

amplitude contrast. Other discussions of coherence issues have been

provided by (Heck et al., 1998; Chao et al., 2003).

3.3.2 Fourier Optics Treatment

Partially coherent imaging by a microscope can be described generally

by the methods of Fourier optics (Wilson et al., 1984; Goodman 1985;

Born and Wolf, 1999). This method uses a real-space and a frequency-

space description of waves in which frequencies (u) are closely

related to directions (θ) according to the general (1D) relation u =

sin θ/l. Following Chapman et al. (1996c), we consider ﬁ rst a STXM

with amplitude point spread function h(x) imaging a sample of ampli-

tude transparency t(x). Using capital letters to represent Fourier trans-

forms, the pupil function of the lens is H(u) where u is the general

frequency coordinate, that is conjugate to the object-plane spatial coor-

dinate x and has a maximum value of NA/l where NA refers to the

beam-limiting lens. Any point in the lens pupil or the detection plane

can be represented by a u value. Since the detector in a STXM is placed

in the far ﬁ eld of the X-ray focal spot, the diffraction pattern formed in

the detection plane in the absence of a sample will be H*(−u). When

0.0

0.2

0.4

0.6

0.8

1.0

MTF

05101520 25

Spatial frequency (µm)

-1

Horiz. (theory)

Vert. (theory)

Horiz. (exp.)

Vert. (exp.)

33 nm feature

Figure 13–21. Measured and calculated modulation-transfer function for

STXM imaging with a nickel zone plate of outer zone width 45 nm and diam-

eter 100 nm. The calculated curve was derived from the known zone plate

aperture function and the size and distance of the source pinhole. (Reprinted

Chapter 13 Principles and Applications of Zone Plate X-Ray Microscopes 879

the sample is present and the spot is at x

, the wave ﬁ eld immediately

behind the sample is h(x)t(x − x

) and the ﬁ eld in the far-ﬁ eld detection

plane is given by the Fourier transform of that. The detected intensity

is therefore

F(u,x

) = |H(u)⊗

T(u)e

2πix

(33)

where ⊗ represents convolution and the convolution and shift theo-

rems have been used. The same quantity F(u,x) can also be represented

in another useful way. By inserting the representations of H(u) and

T(u) as Fourier integrals into the convolution integral Eq. (33) and using

the Fourier-integral deﬁ nition of the delta function (Born and Wolf,

1999) and then its sifting property, we obtain (Chapman et al., 1996c)

F(u,x) = |h(x)⊗

t(x)e

−2πix.u

, (34)

The ﬁ rst of the above two equations represents the diffraction pattern

formed in the detection plane by a STXM at each scan position as

F(u,x

), regarded as a function of u for a given x

. The second equation

represents a coherent image in a TXM, for illumination direction u, as

F(u,x), regarded as a function of x for a given u. In the ﬁ rst case the

exponential represents the scan shift x

and in the second case it rep-

resents the incoming plane wave at direction u. This optical equiva-

lence of the STXM and TXM is known as “reciprocity” and is discussed

further in Section 3.3.4. To get the delivered intensity image I(x) in

either case one has to integrate the signal in the detection plane over

the particular distribution of u values that are used. That is in STXM

we integrate over the intensity response function of the detector |D(u)|

while in TXM we similarly integrate over the intensity distribution in

u delivered by the source |S(u)|

IFDd

IFSd

STXM

DET

TXM

SOURCE

and

xuxuu

()

()()

()

()()

∫

(35)

If the condenser is approximately incoherently illuminated (as speci-

ﬁ ed in §10.5.1 Eq. 13 of (Born and Wolf, 1999) for example), which is

often the case for TXMs, (Schneider, 1998; Vogt et al., 2001a), then the

effective source (Hopkins, 1957), |S(u)|

, will be the condenser lens

aperture function. The expression for the fully incoherent bright ﬁ eld

image (|D(u)|

= 1 or |S(u)|

= 1) is the same in both TXM and STXM and

is obtained by inserting Eq. (33) into Eq. (35) and applying Parseval’s

theorem (Chapman et al., 1996c)

(x) = |h(x)|

⊗

|t(x)|

(36)

The coherent bright ﬁ eld image is available from a STXM by using an

axial point detector and from a TXM by using an axial point source.

Both are given by F(0,x) although neither is widely used in X-ray

microscopy. The process of integrating over S or D, which is carried

out automatically by the hardware of the TXM or STXM, is generally

convenient but it destroys potentially useful information about the

880 M. Howells et al.

sample. A procedure for capturing this information, by storing the

full detection-plane pattern at every pixel position of the STXM image,

has been described and implemented to obtain phase- and amplitude-

contrast images by Chapman etal. (1996a). The speed of the procedure

was limited by the speed of early 1990s computers but, given the im -

provement of computers since then, it may well be time to re-examine

this approach (see Section 3.1.3). Eq. (34) and Eq. (36) show respectively

that coherent imaging is linear in the amplitude and incoherent imaging

is linear in the intensity. On the other hand, as we see below, partially

coherent imaging is not linear in either.

3.3.3 Contrast Transfer

In the case that we do not have |D(u)|

= 1 or |S(u)|

= 1, the above pro-

cedure used to obtain Eq. (36) does not lead to such a simple result but

rather to the following expression representing partially coherent

imaging in a STXM (Kintner et al., 1978; Wilson and Sheppard, 1984;

Born and Wolf, 1999).

ICTTedd

xmpmp mp

mpx

()

(

)

()

(

)

∫∫∫∫

−∞

+∞

−−

()

⋅

[]

2π

(37)

CDHHdmp u u m u p u;

(

)

()

−

(

)

−

(

)

−∞

+∞

∫∫

(38)

For a TXM S replaces D in the last equation. The integration variables

m and p in Eq. (37) are frequencies similar to u but m represents a ray

incident on the sample while p represents a ray emerging from it. The

ranges of frequencies included in these beams by the form of S or D

determine the range of periodicities (m–p) in the sample that contrib-

ute to the image and thus determine the extent of the MTF in frequency

space. The function C(m; p) is known in optics as the transmission

cross coefﬁ cient (Born and Wolf, 1999) or the partially coherent trans-

fer function (Wilson and Sheppard, 1984) and provides a sample-

independent description of the effect of both the illumination and the

optical system on the transfer of information from object to image. It

is not a true transfer function, since the transfer is not linear, but is a

member of a wider class of “bilinear transfer functions.” Such func-

tions are described, for example, by (Saleh, 1979) and have been applied

to partially coherent X-ray imaging by Vogt et al. (2001a).

C(m; p) is widely used in the optical and electron microscopy com-

munities and its properties have been worked out in detail; see for

example (Sheppard and Wilson, 1980; Wilson and Sheppard, 1984). It

is normally a 4D function but in the case of a 1D object it becomes the

2D function C(m;p). The value of C(m;p) is then equal to the overlap

integral of the three appropriately shifted aperture functions in the

integrand of (38) (Kintner et al., 1978; Wilson and Sheppard, 1984; Born

and Wolf, 1999). For many cases of interest in both TXM and STXM,

all three are circular disks or annuli (Figures 13–22 and 13–23). For the

ideally incoherent bright-ﬁ eld image the value of D or S is taken to be

unity for all frequencies and the overlap then depends only on the

Chapter 13 Principles and Applications of Zone Plate X-Ray Microscopes 881

abc

-4

-2

-4

-2

-4

-2

-4

-2

Figure 13–22. Imaging of a one-dimensional

cosine amplitude grating object using a STXM.

The top row shows the signal in the detection

plane. The center row shows gray-level plots of

C(m, p) in m–p space overlaid with the support

boundary of C(m, p) (solid lines) and the spectra

T(m)T*(p) as in Eq. (37) (spots). The middle row

shows bright ﬁ eld and the bottom row dark

ﬁ eld. The three columns correspond to grating

frequencies that are (a) >2, (b) between 1 and 2

and (c) <1 expressed in units of the maximum

values of m and p which are both equal to NA/l.

permission from Elsevier.)

Figure 13–23. Bright-ﬁ eld (a) and dark-ﬁ eld (b)

partially coherent transfer functions for a 1D

object and an annular lens with inner radius

equal to 0.44 times the outer (after Chapman

et al., 1996c). The function C(m, p) is plotted

against m and p, expressed as multiples of their

maximum value NA/l. (Reprinted from

Elsevier.)

882 M. Howells et al.

difference m–p of the shifts of H and H*. That is, there is only one

response to the sample frequency s = m − p irrespective of m, which

indicates a linear system with MTF equal to C(m–p;0)/C(0;0). For forms

of D or S corresponding to partial coherence, the system is not linear.

On the other hand a dark-ﬁ eld conﬁ guration must have detector (or

source) and lens aperture functions which have zero overlap at m = p

= 0. For example D or S could be the Babinet inverse of H. For circular

functions of the latter type C(m;p) = 0 if sign(m) ≠ sign(p). Examples of

both bright- and dark-ﬁ eld transfer functions for aperture geometries

that are representative of a STXM and that show the above character-

istics are given by Chapman et al. (1996c) (Figure 13–23). The response

of the same systems to a grating-like object are also given (Figure 13–

22). Dark-ﬁ eld STXM is particularly well suited to imaging samples

with small features such as gold labels that scatter by large angles

(Chapman et al., 1996b). The procedures outlined above allow the cal-

culation of the MTF and the resolution behavior of both types of X-ray

microscope based on a knowledge of the resolution-determining lens

and the geometry of the source or detector. It is noteworthy that, as in

other types of microscope, the resolution does not depend on aberra-

tions of the condenser if there is one. As noted in Section 3.1.2 and

illustrated in Figure 13–17, the placement of a ring aperture and phase

ring to get Zernike phase contrast in a TXM may be modeled as modi-

ﬁ cations of the source and lens aperture functions. By this means the

above method of analysis may be applied to this case as well (Mondal

and Slansky, 1970; Sheppard and Wilson, 1980; Morrison, 1989a).

3.3.4 Reciprocity

The general conclusion of the above analysis is that the optical systems

of the TXM and STXM are the same with the position of the lens, before

or after the sample, interchanged and the role of the source and detec-

tor interchanged. This is the “reciprocity” relationship (Zeitler and

Thomson, 1970) that has long been recognized in the visible-light and

electron imaging communities and has been explained in the context

of X-ray imaging by Morrison (1989a; Morrison et al., 2002). Thus we

might expect that, given identical resolution-determining lenses, a

TXM and a STXM (both operating in incoherent bright-ﬁ eld mode)

could equally well utilize wide-angle beams and get good resolution.

For TXM the requirement would be that the condenser should deliver

a wide angle to the sample and for STXM that the detector should

collect a wide angle from the sample. However, in the past, the practical

realization of a wide-angle condenser for a TXM has been much harder

than a wide-angle detector for a STXM as we discussed in the con-

denser zone plate section above.

In practice the TXM/STXM relationship is not quite as symmetrical

as the above account suggests because of the general use of objective

zone plates with a central stop for STXM (Section 3.1.3) but not for

TXM. The stop produces a point-spread function, which has a narrower

central peak but larger side lobes. As a consequence the frequency

response (the MTF, see Figure 13–21) is increased in the high-frequency

and decreased in the low-frequency region.

Chapter 13 Principles and Applications of Zone Plate X-Ray Microscopes 883

3.3.5 The Inﬂ uence of Coherence on Resolution

Calculations of the transfer function as an overlap area of three aper-

ture functions in the integrand of Eq. (38) were discussed in Section

3.3.3. For standard TXM, these functions are circular and two of them

are the same. One can therefore follow (Hopkins, 1957) and characterize

the illumination by a coherence parameter s deﬁ ned by the ratio of the

condenser and objective numerical apertures or s = NA

/NA

. Full

coherence is represented by σ = 0 and full incoherence by σ = ∞,

although s = 1 is usually sufﬁ cient to get close to fully incoherent

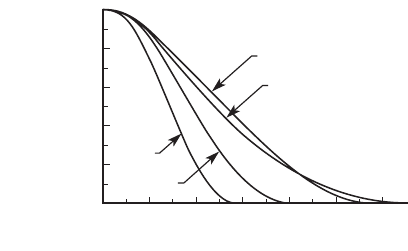
behavior. We start by considering the modulation (the percent dip in

the valley between the peaks) for a two-point object with separation

0.61l/NA

. The modulation is 26.5% for incoherent illumination (Born

and Wolf, 1999) and according to the Rayleigh criterion, the two points

are just resolved. It is common practice (Born and Wolf, 1999) to extend

the Rayleigh criterion to other pairs of objects and deﬁ ne them as

resolved if the modulation is at least 26.5%. An example is the two-point

object with in-phase coherent illumination for which the just-resolvable

separation is 0.82l/NA

. Further detail of this can be seen from the plots

in Figure 13–24 (Jochum and Meyer-Ilse, 1995). An important example

for X-ray imaging is the modulation due to a periodic object, in particu-

lar a square-wave transmission object. Such an object can either be

prepared by standard lithography methods (Jacobsen et al., 1991) or, for

ﬁ ner line widths, by preparing thin cross-sections of synthetic multilay-

ers (Chao et al., 2003), to yield resolution test patterns for an X-ray

microscope. If the resolution is deﬁ ned as the half period of the ﬁ nest

square wave that can be i mage d w it h 26. 5% modu lation and is expressed

as k

l/NA

, then according to (Chao et al., 2005), the diffraction-limited

value of k

is 0.5 for a coherent system (s = 0) and 0.4 for s = 0.38 (the

actual value for XM-1 illuminating the 15 nm zone plate). Thus the dif-

fraction-limited resolution of their experiment was 0.8∆r

while the

0.8 1 1.2 1.4

1/d

1.6 1.8 2

0.8

0.6

0.4

0.2

Contrast

σ = 1

σ = 0

σ = 0.5

σ→

∞

Figure 13–24. Image contrast as a function of 1/d where d is the point separa-

tion of a two-point object imaged by a lens with a circular pupil and coherence

parameter σ equal to 0 (coherent case), 0.5, 1 and inﬁ nity (incoherent case). d

is expressed in units of l/NA. Note that the Rayleigh resolution corresponds

to 15.3% intensity contrast (deﬁ ned as (I

max

− I

min

)/(I

max

+ I

min

)), which is the

same as 26.5% modulation. It occurs at d = 0.61l/NA for both s = 1 and s →

from Optical Society of America.)

884 M. Howells et al.

achieved value was about 1.0∆r

(<15 nm). The data demonstrating the

achieved resolution are shown in Figure 13–13. By reciprocity, the same

arguments about the value of the diffraction-limited resolution would

apply for a STXM in incoherent bright ﬁ eld using the same zone plate.

With a large enough detector one would achieve s = 1 and the same

diffraction-limited resolution as a TXM with s = 1.

3.3.6 Coherence in Zernike Phase Contrast

We return now to the question of the choice of width and radius for

the two rings in a Zernike phase-contrast conﬁ guration of the TXM,

or, equivalently, how much coherence is desirable in this case. This

choice has been discussed by (Mondal and Slansky, 1970) and is essen-

tially a trade off between light collection and the distorting effects of

the fact that the phase ring must have ﬁ nite area, which applies an

unintended phase change to a certain portion of the diffracted light

causing the so-called halo effect (Wilson and Sheppard, 1981). It is

generally thought that one needs very little coherence, that is, the ring

aperture can leave a large fraction of the condenser area open. This is

true if the requirement is merely to make otherwise invisible phase

features, especially phase jumps, become visible. However, with low

coherence, a phase step is rendered as a double-peaked zero-crossing

function and a phase rect function is rendered as two such double

peaks. How much coherence do we need to get anything resembling a

faithful rendition of the object? We have not found much attention to

this point in the literature but the treatment by Martin (1966) provides

an answer, which is conﬁ rmed by our own computer modeling. To get

a rendition of a rect function that looks like the original function one

needs to have the coherence width w

= lf

cond

/∆r

ring

of light arriving at

the sample at least equal to the width of the rect function.

3.3.7 Propagation-Based Phase Contrast

Another way to achieve phase contrast is to exploit the exp[iπ(x

+ y

lz] phase shifts that occur in the (x, y) plane as a result of the propaga-

tion of a coherent waveﬁ eld through a distance z. This is exploited in

X-ray holographic microscopy which has had many successes (Aoki

and Kikuta, 1974; Joyeux, et al. 1988; Jacobsen et al., 1990; McNulty et

al., 1992; Snigirev et al., 1995; Lindaas et al., 1996; Eisebitt et al., 2004)

but which is so far not used for routine X-ray imaging. The exception

is in the use of holography for phase contrast tomography at higher X-

ray energies, where Cloetens and coworkers have achieved consider-

able success in routine micrometer-resolution tomography using a

phosphor/lens/CCD detector system (Cloetens et al., 1999). While it

lies beyond the scope of the present article’s emphasis on zone plate

X-ray microscopy, this unique approach is providing impressive 3D

reconstructions of difﬁ cult specimens including foams.

3.4 Tomography in X-Ray Microscopes

3.4.1 Principle of Operation

As was noted in Section 2.4.5 on hard X-ray zone plates, the transverse

resolution of a zone plate operated in ﬁ rst diffraction order is given by

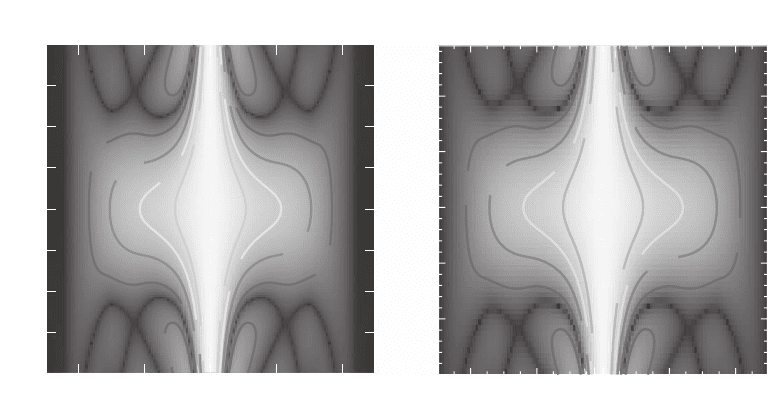
Chapter 13 Principles and Applications of Zone Plate X-Ray Microscopes 885

0.61l/NA = 1.22∆r

, and the depth of focus is 2l/(NA)

= 8(∆r

)

/l. Since

present zone plates have outermost zone widths ∆r

that are much

larger than the wavelength λ, this means that the depth of focus is nec-

essarily large compared to the resolution as can be seen by the illustra-

tion of the 3D modulation transfer function in Figure 13–25. This

provides an opportunity for 3D imaging if the object is smaller than the

depth of focus because a 2D image can then be interpreted as providing

a simple projection through the specimen, which is precisely what con-

ventional tomography requires at each viewing angle. Tomography

with electron microscopes is long established, and following earlier

demonstrations by Haddad et al. (1994) using the Stony Brook STXM

and Lehr (1997) using the Göttingen TXM, a number of groups are now

using X-ray microscopes for tomographic studies of frozen hydrated

biological specimens and integrated circuits, among other applications

that will be described below in Section 4. However, although the tech-

nique used in these studies is improving, they have still not reached the

resolution achieved by the same microscopes in 2D.

3.4.2 The Depth-of-Focus Limit

Given the successes achieved and the amount of current interest, what

are the issues to be faced in improving the resolution of tomography

10%

30%

50%

70%

10%

50%

70%

Contrast versus defocus:

=45 nm,

=2.5 nm

-20 -10 0 10 20

Spatial frequency (

µm

-1

)

-8

-6

-4

-2

Defocus (

µm)

10%

30%

50%

70%

10%

50%

70%

-40 -20 0 20 40

Spatial frequency (

µm

-1

)

-1

Defocus (

Contrast versus defocus:

=20 nm, λ=2.5 nm

30%

Figure 13–25. Properties of soft X-ray tomography using zone plate optics. At the left is shown the

3D modulation transfer function for monochromatic, spatially incoherent bright-ﬁ eld imaging with a

45-nm-outer-zone-width zone plate with a half-diameter central stop, as a function of depth. One can

see that the good in-focus frequency response is preserved over a total depth of about 8 µm. This is

useful for many tomography experiments that rely on the fact that the delivered image is a projection

of the object. At the right is the same information for a 20-nm-zone plate; as can be seen, the ﬁ gure

scales quite well from the ﬁ gure at the left according to the square of the ratio of the ﬁ nest zone widths.

With a 20-nm-zone plate and monochromatic illumination, good frequency response is only preserved

over a depth of about 0.5–1 µm which is much more restrictive, illustration the challenges of improved

Blackwell Publishing.)

886 M. Howells et al.

in X-ray microscopes? One of them concerns the same depth of focus

that makes such tomography straightforward. To our knowledge all

demonstrations of soft X-ray tomography reconstructions have used

zone plates with outermost zone width ∆r

no ﬁ ner than 35 nm, so that

the depth of focus in the water window region is at least 4 µm which

has been comparable to the specimen size. As higher resolution zone

plates are employed, the depth of focus will decrease as the square of

improvements in transverse resolution, so that a 15 nm outermost-

zone-width zone plate would have a depth of focus of about 0.8 µm.

This approaches the ∼0.5 µm thickness accessible to cryo electron

tomography of frozen hydrated cell regions at 6–8 nm resolution

(Grimm et al., 1998; Medalia et al., 2002) and thus would seem to leave

a much-reduced “window of opportunity” for soft X-ray tomographers

and apparently deny them the important goal of high-resolution, 3D

imaging of intact eucaryotic cells.

The depth-of-focus limit evidently poses a considerable challenge to

those who would exploit zone plate X-ray microscopes for tomography.

Accordingly we discuss in the sections that follow several different

approaches to dealing with the challenge.

3.4.3 Avoiding the Depth-of-Focus Limit by Reconstructing a

Partial Volume

Zone-plate-microscope X-ray tomography as described above is based

on geometrical optics and is mathematically identical to the technique;

Computed Axial Tomography (CAT). Therefore, following an estab-

lished CAT procedure (see for example Ritman et al., 1997), it is possi-

ble to reconstruct partial volumes that are embedded in a larger overall

object. This has been done in the X-ray microscope context by Xradia

Inc. In this case the depth-of-focus limit applies to the partial volume,

rather than the whole volume, and the signals generated by the out-of

focus parts of the sample reduce, after combining all members of the

tilt series, to a smooth background. The size of the region that is always

in focus will be roughly a sphere of diameter equal to the depth of

focus.

3.4.4 Avoiding the Depth-of-Focus Limit by

Wide-Band Illumination

In fact, the depth of focus calculation given above is for monochromatic

illumination, which is applicable to demonstrations of tomography of

frozen hydrated cells in a STXM with a high-energy-resolution mono-

chromator (Wang et al., 2000). In some existing soft X-ray TXMs using

the zone plate condenser as a linear monochromator, an energy resolv-

ing power of E/∆E ≈ 200 has been used for objective zone plates with

N = 375 zones (the recommended bandwidth for such an objective

would usually have been E/∆E > N, (Thieme, 1988). However, Weiss et

al.(2002) have shown that use of E/∆E ≈ 200 leads to signiﬁ cant changes

of the modulation transfer function (MTF) as a function of defocus

(similar results for different cases have been given by Schneider et al.

(2002a)). In their calculations for a zone plate with 40 nm outermost

zone width, the MTF at a spatial frequency of 15 µm

−1

(corresponding

to a spatial half-period of 33 nm) declines from about 0.28 in focus to

Chapter 13 Principles and Applications of Zone Plate X-Ray Microscopes 887

about 0.015 at a defocus of 4 µm in the monochromatic case. When the

bandwidth is increased to E/∆E ≈ 200, the MTF at 15 µm

−1

is reduced

in focus to only about 0.11 but at the same 4 µm defocus it degrades

much less to 0.08. Therefore these calculations show that, although the

transverse resolution and efﬁ ciency for the collection of structural

information, are both made worse by the use of high-bandwidth radia-

tion, the depth of ﬁ eld is improved. (To our knowledge no calculations

have yet addressed the possibly interesting question of how this trad-

eoff with nonmonochromatic illumination compares with the tradeoff

resulting from using a lower or higher resolution zone plate). In

summary, it will require further investigation to determine whether

manipulation of the bandwidth can enable signiﬁ cant improvements

to the tomographic resolution without reduction of the reconstructible

sample volume.

3.4.5 Avoiding the Depth-of-Focus Limit by

Through-Focus Deconvolution

One possible approach to beat the depth of focus limit is to use through-

focus deconvolution as is done in light and electron microscopy. In

electron microscopy, the recording of defocus image sequences is

routine; each defocus provides positive and negative phase contrast at

various bands of spatial frequencies along with zeroes in the transfer

function, and the combination of several images can provide a com-

plete image of the specimen (Reimer, 1984). In ﬂ uorescence light

microscopy, through-focus image sequences can yield a high quality

3D image through the use of deconvolution of the 3D point spread

function (Agard and Sedat, 1983; Carrington et al., 1995). However,

there are important differences between these examples and the situ-

ation present in X-ray microscopy. In electron microscopy, this approach

is usually applied to thin samples for which phase contrast dominates

(indeed the specimen focus can be quickly estimated by looking for a

minimum in image contrast). In light microscopy, the use of ﬂ uores-

cence means that the object is a sparse, pure-real function (incoherent

emission from independent ﬂ uorescence emitters with no sensitivity

to the relative phase of the illumination) so that the deconvolution can

be done based on the intensity point spread function. While some form

of generalized through-focus deconvolution may provide the needed

breakthrough, quantitatively reliable results such as are needed for

assembly into a tomographic reconstruction will have to account for

the fact that biological specimens imaged at water-window energies

produce both absorption and phase contrast so one will require exact

knowledge of the complex bilinear transfer function of the zone plate

optic and illumination system. In other words, the problem of 3D

deconvolution of a strongly absorbing, optically thick, complex object

with partial coherence is much more difﬁ cult than the cases in which

optical sectioning is typically used at present.

3.4.6 Avoiding the Depth-of-Focus Limit by Use of Higher

Energy X-Rays

The use of shorter wavelengths (higher X-ray energies) to increase the

monochromatic depth of ﬁ eld 8(∆r

)

/l is a guaranteed way to extend