Hawkes P.W., Spence J.C.H. (Eds.) Science of Microscopy. V.1 and 2
Подождите немного. Документ загружается.

Chapter 9 Photoemission Electron Microscopy (PEEM) 695
Zach, J. and Haider, M. (1995). Optik 98, 112–118.
Zharnikov, M., Frey, S., Heister, K. and Grunze, M. (2002). J. Electron Spectrosc.
Rel. Phenomena 124, 15–24.
Zworykin, V.K. and Kosma, V. (1945). Electron Optics and the Electron Microscope
(Wiley, New York).
696
10
Aberration Correction
Peter W. Hawkes
1 Introduction
It has been known since the early days of electron optics that the rota-
tionally symmetric lenses employed in electron microscopes and
similar instruments suffer from severe aberrations that cannot be
eliminated by skillful lens design (Scherzer, 1936). Immense effort has
been devoted to fi nding lenses with small aberrations and devising
aberration correctors. The original demonstration that the two most
important aberrations, spherical and chromatic, cannot be eliminated
required that several conditions be satisfi ed and, by relaxing one or
the other of these conditions, correctors can be designed. A near-
exhaustive list was published by Scherzer (1947) and reviews charting
trends in thinking about aberration correction and progress in imple-
menting correctors are to be found in Septier (1966), Hawkes (1980),
and Hawkes and Kasper (1989). These contain very full accounts of
earlier attempts to correct aberrations with extensive reference lists and
the material presented there is not always reproduced here. In particu-
lar, a survey of attempts to build apochromats and aplanatic lenses by
H. Rose and colleagues in Darmstadt is to be found in the article by
Hawkes (1980).
The types of corrector that seem most promising today are examined
below but fi rst, we describe the various kinds of aberration and explain
why they are important. We then look more closely at the aberration
coeffi cients themselves, which leads naturally to a study of the
correctors.
Some familiarity with basic electron optics is assumed here. In par-
ticular, the reader is expected to be acquainted with the paraxial prop-
erties of lenses and the cardinal elements that characterize them. The
Handbook of Charged Particle Optics edited by J. Orloff (1997) is recom-
mended for readers who wish to brush up their knowledge of electron
lenses, notably the chapters by Munro, Tsuno, Lencová, and Hawkes.
For very full accounts, see Hawkes and Kasper (1989) and Rose
(2008).

Chapter 10 Aberration Correction 697
2 Types of Aberration
Lens aberrations are of three kinds: geometric aberrations, chromatic
aberrations, and parasitic aberrations
2.1 Geometric Aberrations
An ideal lens would provide point-to-point mapping of the structure
of an object into an image and such imaging is indeed predicted by
the simplest approximate description of the effect of a lens on an elec-
tron beam, the paraxial approximation. This is valid provided that the
electrons remain close to the optic axis (the axis of symmetry in the
case of a round lens) and that the electron trajectory remains inclined
at a small angle to this axis. When the electrons depart too far from
the axis or the trajectories are inclined at a steeper angle, the paraxial
approximation is perturbed by geometric aberrations.
In the paraxial approximation, electrons (of charge −e and rest
mass m
0
) satisfy the linear, homogeneous, second-order differential
equation
(1)
with an identical equation for y(z), in which φ(z) is the axial electro-
static potential and B(z) is the magnetic induction on the optic axis,
which coincides with the coordinate axis z. Primes denote differentia-
tion with respect to z. The fi eld and potential expansions are given in
Appendix I; for derivations of these, see Hawkes and Kasper (1989,
Chapter 7). Since the chapter by Rose in High-Resolution Imaging and
Spectrometry of Materials edited by F. Ernst and M. Rühle is a very rele-
vant reference (Rose, 2002c) to much of the material presented here, the
relation between his notation and that adopted here is also given. The
relativistically corrected potential
ˆ
φ is given by
ˆ
φ = φ(1 + εφ) (2)
where ε = e/2m
0
c
2
≈ 0.1 MV
−1
; γ = 1 + 2εφ and η = (e/2 m
0
)
1/2
≈ 3 ×
10
5
C
1/2
kg
−1/2
. The distances x(z) and y(z) are the rotating coordinates
routinely employed in the study of round magnetic lenses.
Such differential equations have the general solution
x(z) = Ax
1
(z) + Bx
2
(z)
where x
1
(z) and x
2
(z) are linearly independent solutions of Eq. (1) and
A, B are constants. It is frequently convenient to choose for x
1
(z) and
x
2
(z) the solutions g(z) and h(z) that satisfy the boundary conditions
g(z
o
) = h′(z
o
) = 1
(3)
g′(z
o
) = h(z
o
) = 0
where z
o
is the object plane, whereupon we have
x(z) = x
o
g(z) + x′
o
h(z)
(4)
y(z) = y
o
g(z) + y′
o
h(z)
d
dz
ˆ
φ
1/2
′
x
()
+
γ
′ ′
φ
+
η
2
B
2
4
ˆ
φ
1/2
x = 0
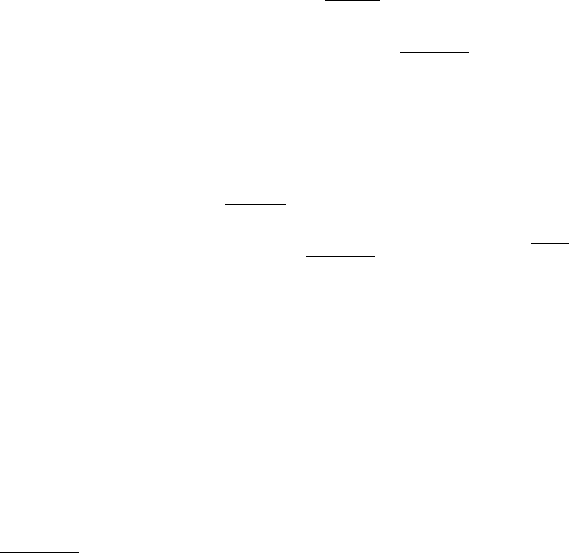
698 P.W. Hawkes
The cardinal elements of the lens, its focal lengths and the positions of
its focal planes and principal planes, are defi ned with the aid of the
rays g(z) and h(z). It is convenient to write u = x + iy and it can readily
be shown that
u
u
zz
f
T
f
zz
f
u
u
F
′
=
−
−
−
′
Fi
i
i
oo
i
o
o
12
1/
(5)
If u is proportional to u
o
for all values of the gradient u′
o
, the matrix
element T
12
vanishes. The plane z is then said to be conjugate to z
o
and
we write z = z
i
. The matrix equation then collapses to
u
u
zz
f
f
zz
f
u
u
F
i
i
Fi i
i
i
oo
i
o
o
′
=
−
−
−
′
0
1/
=
−
′
M
f
f
fM
u
u
0
1/
i
o
i
o
o
(6)
Here, M denotes the magnifi cation, g(z
i
) = M, f
o
and f
i
are the object and
image focal lengths, and z
Fo
and z
Fi
are the object and image foci. (For
more details of paraxial optics, see Chapters 16 and 17 of Hawkes and
Kasper, 1989.) In the case of purely magnetic round lenses, f
o
= f
i
and
we denote the focal length by f.
The next higher approximation includes terms of third order in u
o
and u′
o
. Systems with a straight optic axis have no second-order terms
and the rotational symmetry about the optic axis restricts the permit-
ted third-order terms to the following:
(7)
The spherical aberration term is of particular concern since it does
not vanish or even dwindle for object points close to or on the axis.
This is the region that is imaged in high-resolution operation. We
examine this aberration closely in a later section. The other terms are
of decreasing interest for objective or probe-forming lenses and,
moreover, the coma (next in importance after the spherical aberration)
can be avoided. Lenses have a “coma-free plane,” the exact position
of which is determined by the relative magnitudes of the spherical
aberration and coma coeffi cients. In practice, for magnetic lenses, it
falls within the lens fi eld, upstream from the image focus (the “diffrac-
tion plane”). Specifi cally, let us suppose that the aberrations are
expressed in terms of ray position in the object plane, z = z
o
and
some aperture plane, z = z
a
. The paraxial solutions appearing in
the aberration integrals will then be s(z) and t(z), which satisfy the
conditions
uMu
M
Cu x y
Kikux
io
oo o
oo
spherical aberration
−
=
′′
+
′
()
(
)
++
(
)
′
22
2
222 2
+
′
()
+−
(
)
′
()
++
(
)
′
(
)
+
∗
yKikuu
Aiauu
Fx
ooo
o
2
o
coma
astigmatism
oo
2
o
2
o
oo
2
o
2
field curvature
distortion
+
()
′
(
)
++
(
)
+
()
(
yu
Didux y
))

Chapter 10 Aberration Correction 699
s(z
o
) = t(z
a
) = 1
(8)
s(z
a
) = t(z
o
) = 0
If another aperture position is selected, z = z¯
a
, the aberration coeffi cients
will have exactly the same structure but the appropriate paraxial solu-
tions will now be s¯(z) and t
¯
(z),
s¯(z
o
) = t
¯
(z¯
a
) = 1
(9)
s¯(z¯
a
) = t
¯
(z
o
) = 0
Since there can be only two linearly independent paraxial solutions,
we must be able to write
s¯(z) = αs(z) + βt(z)
(10)
t
¯
(z) = γs(z) + δt(z)
and obviously α = 1 and γ = 0; for β and δ, we have
β = −s(z¯
a
)/t(z¯
a
)
(11)
δ = 1/t(z¯
a
)
It is then easy to show that the coma coeffi cient for z = z¯
a
, K(z¯
a
), is related
to that for z = z
a
, K(z
a
), as follows:
K(z¯
a
) ∝ K(z
a
) + βC
s
(z
a
) (12)
The coma-free point is thus situated at the point for which
sz
tz
Kz
Cz
()
()
()
()
a
a
a
sa
=
(13)
The distortion can be important in projector lenses, in which the tra-
jectories may be relatively far from the axis while the gradient will be
very small at high magnifi cation. Astigmatism and fi eld curvature are
mainly of importance in devices in which the size of the fi eld is a major
preoccupation, such as lithography.
For quadrupoles, the situation is slightly more complicated. A quad-
rupole usually consists of four electrodes or four magnetic poles,
though many other confi gurations that create quadrupole fi elds exist
(see, for example, Hawkes, 1970 or Baranova and Yavor, 1989). For con-
venience, we assume throughout that the quadrupole is disposed in
such a way that the converging and diverging planes coincide with the
x–z and y–z planes (Figure 10–1). The paraxial properties of the quad-
rupole are then characterized by equations of motion for x(z) and y(z)
that are uncoupled but no longer identical. They are again linear,
homogeneous, second-order differential equations and hence have
solutions analogous to those for round lenses. Now, however, we have
two sets of cardinal elements, one set for the x–z plane and a second
set for the y–z plane. These equations take the form
(14)
d
dz
ˆ
φ
1/2
′
x
()
+
γ
′ ′
φ
−2
γ
p
2
+ 4
η
Q
2
ˆ
φ
1/2
4
ˆ
φ
1/2
x = 0
d
dz
ˆ
φ
1/2
′
y
()
+
γ
′ ′
φ
+ 2
γ
p
2
− 4
η
Q
2
ˆ
φ
1/2
4
ˆ
φ
1/2
y = 0
700 P.W. Hawkes
Figure 10–1. Quadrupoles. (a) Quadrupole orientation. The paraxial equations of motion are uncou-
pled when the x–z and y–z planes coincide with the planes of symmetry of electrostatic quadrupoles
and fall midway between the poles of magnetic quadrupoles. (b) Appearance of a mixed magnetic–
electrostatic quadrupole.
b)
a)
++
x
y
a
–
–
b
x
–
N
N
y
S
s
Chapter 10 Aberration Correction 701
in which the functions p
2
(z) and Q
2
(z) characterize the potential and
fi eld distributions (see Appendix I). We can now write
xz
xz
zz
f
f
zz
ix
ix
x
ix
x
x
x
()
()
/
()
()
()
(
′
=
−
−
−
Fi
i
i
o
Fo
0
1
))
()
()
()
()
/
f
x
x
M
f
f
f
x
x
x
x
x
i
o
o
i
o
i
′
=
−
0
1
MM
x
x
x
′
o
o
(15a)
and
yz
yz
zz
f
f
zz
iy
iy
y
iy
y
y
y
()
()
/
()
()
()
(
′
=
−
−
−
Fi
i
i
o
Fo
0
1
))
()
()
()
()
/
f
y
y
M
f
f
f
y
y
y
y
y
i
o
o
i
o
i
′
=
−
0
1
MM
y
y
y
′
o
o
(15b)
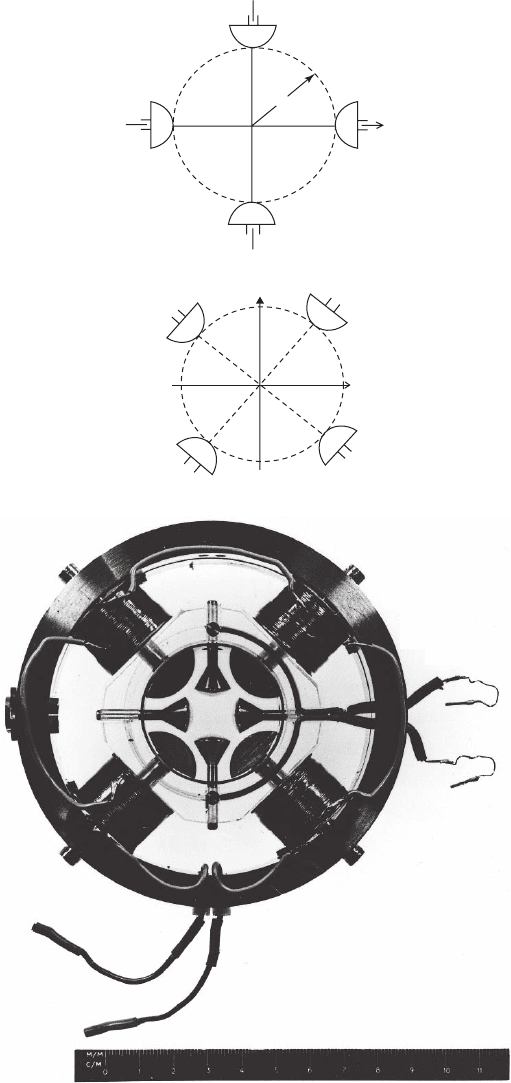
Figure 10–1. Continued (c) Formation of a line image in a magnetic quadrupole; the arrows show the
directions of the currents in the windings. (After Hawkes and Kasper, 1989, courtesy of Elsevier/
Academic Press.)
c)

702 P.W. Hawkes
Since the cardinal elements are different in the two planes, the planes
conjugate to a given object plane will not, in general, coincide. The
system is astigmatic and if we operate two quadrupoles in tandem, the
“object” of the second member will be astigmatic. Clearly, if we require
quadrupoles to produce a stigmatic image of an object, we must use
quadrupole multiplets and must somehow arrange that the cardinal
elements of the multiplet are the same in the two planes. One multiplet
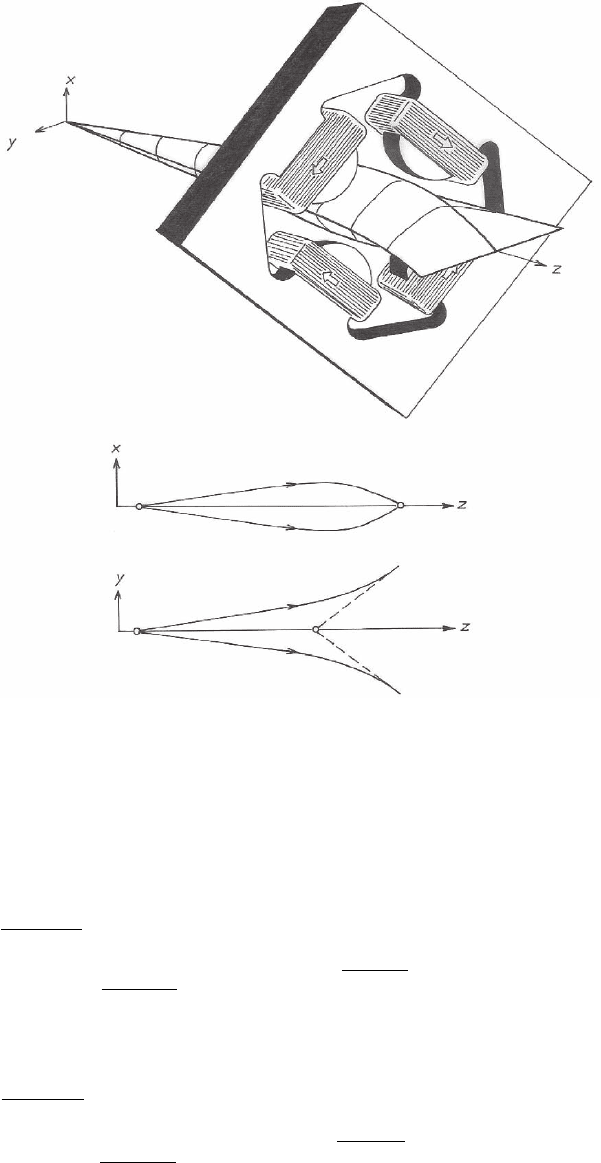
confi guration is of particular importance. It can be shown by symme-
try arguments that if the multiplet is geometrically symmetric and
electrically antisymmetric about its center plane, the focal lengths in
the x–z and y–z planes will be equal. It is then only necessary to satisfy
one condition (coincidence of the focal planes) to render the multiplet
stigmatic. Quadruplets with this property have been extensively
studied and are known as Russian Quadruplets, since their properties
were fi rst investigated by Dymnikov and Yavor (1963) in the Ioffe
Institute in Saint Petersburg (Figure 10–2).
The aberrations of quadrupoles are more numerous than in the case
of round lenses but they fall into the same categories: aperture aberra-
tions (the analogues of the spherical aberration), comas, astigmatisms,
and fi eld curvatures and distortions. Here we consider only the aper-
ture aberrations, since they will be exploited in aberration correctors.
At this point, we note that octopoles, which have eight electrodes or
magnetic poles, also have quadrupole symmetry and should hence be
included in the formalism for the aberrations. They have no linear
effect and hence have no effect on the paraxial behavior.
Our interest here is exclusively with aberration correctors, and we
therefore assume that any multiplets of quadrupoles and octopoles are
stigmatic and that the magnifi cations in the two planes are likewise
equal M
x
= M
y
). In these circumstances, the additional terms arising
from the aperture aberrations take the following form:
∆
∆
x
M
xCx Cy
y
M
yCx Cy
xxy
xy y
=
′′
+
′
()
=
′′
+
′
()
oo o
oo o
22
22
(16)
The other multipoles used for aberration correction are sextupoles
(also known as hexapoles). Like octopoles, they have no linear
mid-plane
Q
1
Q
2
Q
1
Q
2
Figure 10–2. The “Russian” quadruplet. The excitations of the fi rst and last
quadrupoles are equal and opposite, as are those of the second and third
quadrupoles. The quadrupoles are disposed symmetrically about the center
plane.
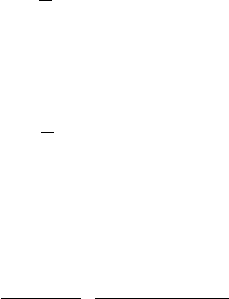
Chapter 10 Aberration Correction 703
effect on charged particles but unlike octopoles (and of course
quadrupoles), their dominant effect is quadratic. Their primary aberra-
tions are third order, like round lenses and quadrupoles, and their
aperture aberration, the aberration that depends only on gradient
and is independent of off-axis distance, has the same nature as
the spherical aberration of round lenses. It is for this reason that sex-
tupoles are potential correctors of C
s
but some way of eliminating the
quadratic effects must be devised. We shall see how this is achieved in
a later section. For extensive discussion of their optical properties, see
Rose (2002c).
Since the sextupoles will be used in conjunction with one or more
round lenses, the paraxial solutions satisfy Eq. (1). We adopt a slightly
different pair of solutions from those of Eq. (2), namely h(x), which, as
before, satisfi es
h(z
o
) = 0, h′(z
o
) = 1 (17a)
and k(z),
k(z
o
) = 1, k(z
k
) = 0 (17b)
where z = z
k
is the coma-free point discussed earlier. The expression
for a general ray becomes
u(z) = Ω
h
h(z) + Ω
k
k(z) (18)
in which Ω
h
and Ω
k
are simply related to the usual object coordinates
(for ample details, see Rose, 2002, which is closely followed here).
When this general ray passes through a sextupole lens, it will be devi-
ated through a distance ∆u, which has the form
∆u = Ω
–
2
h
u
11
+ Ω
–
h
Ω
–
k
u
12
+ Ω
–
2
k
(19)
with
uz hz Hhkdzkz Hhdz
uz hz Hhk
z
z
z
z
11
23
12
2
1
2
() () ()
() ()
=−
=
∫∫
oo
ddz k z Hh kdz
uz hz Hkdzkz Hhk
z
z
z
z
z
z
oo
o
∫∫
∫
−
=−
()
() () ()
2
22
3
1
2
22
dz
z
z
o
∫
(20)
The function H(z) characterizes the fi eld distribution in the sextupoles;
in the most general case (in which both electrostatic and magnetic
sextupoles may be present), H is given by
Hz
ipiq
iP iQ()
()( )( )
()
^
/
/
=−
−++
++
exp
o
31
12
33
12
33
χ
φ
εφ
φ
η
ˆ
(21)
where χ(z) characterizes the usual rotation in magnetic lenses.
All three contributions must vanish if the unwanted second-order
effects of the sextupoles are to be eliminated; this can be achieved if
the four integrals
704 P.W. Hawkes
Hzh k dzn
nn
z
z
() , ,, ,
3
012 3
−
=
∫
and
o
e
(22)
all vanish. The form of these conditions, in two of which h(z) is an even
function while k(z) may be odd, and in the other two the situation is
reversed, indicates that symmetry can be used to eliminate all four
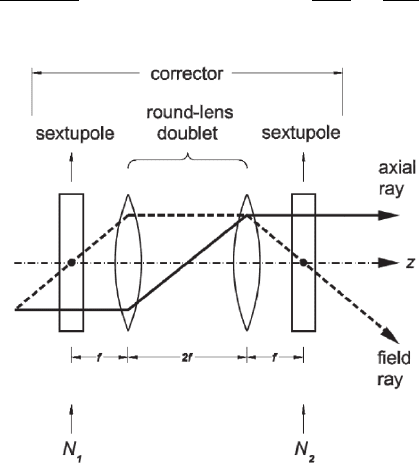
quantities. The simplest arrangement is that shown in Figure 10–3.
Here, one ray is symmetrical within each sextupole but antisymmetric
about the center plane of the combination; the other ray is antisym-
metric about the mid-plane of each sextupole but symmetric about the
center plane of the whole combination. The members of the round-lens
doublet have equal and opposite excitations, chosen in such a way that
the centers of the sextupoles are conjugates, with magnifi cation −1.
Since the sextupole strength is a free parameter, it can, as we shall see
in Section 3.2.2, be used to cancel the spherical aberration of an adjoin-
ing round lens.
2.2 Chromatic Aberrations
Chromatic aberrations are a consequence of the rapid variation of elec-
tron lens strength with electron energy and lens excitation. The elec-
tron beam from the gun will inevitably have some energy spread and
there will be some variation in the lens excitations, however carefully
they have been stabilized. The result is a “chromatic” effect, character-
ized by chromatic aberration coeffi cients, that blurs the image. We can
include this in the paraxial formalism by writing
uMu
M
Cu C iC u
B
B
i
−
=−
′
++
{}
−
o
co D o
()
θ
φ
φ
∆
∆
^
^
0
0
0
0
2
(23)
Figure 10–3. The simplest sextupole arrangement. No second-order aberra-
tions are introduced outside the corrector. (After Rose, 2003c, courtesy of the
author and Springer-Verlag.)
