Hawkes P.W., Spence J.C.H. (Eds.) Science of Microscopy. V.1 and 2

Подождите немного. Документ загружается.

Chapter 10 Aberration Correction 705

in which C

is the (axial) chromatic aberration coefﬁ cient, C

is a

measure of the chromatic aberration of magniﬁ cation, and C

is the

anisotropic distortion. The quantity ∆φ

is a measure of the potential

variation corresponding to the energy spread of the beam and ∆B

represents any ﬂ uctuations in the ﬁ eld strength of the lens caused by

variations of the current. (Here we are considering only magnetic

lenses; a similar reasoning applies to electrostatic lenses.)

We thus have two types of aberration: the chromatic aberration C

which is linear in gradient and hence does not vanish for object points

close to the axis, just like the spherical aberration; and the complex

chromatic aberration of magniﬁ cation (C

+ iC

), analogous to the dis-

tortion in that it is independent of gradient. We can therefore expect

that the chromatic aberration, like the spherical aberration, will impose

a limit on the resolution attainable in very high resolution work. In

practice, it deﬁ nes an “information limit.” which, in instruments that

have not been corrected for spherical aberration, is usually less severe

than the limit imposed by spherical aberration. With the arrival of

spherical aberration correctors, however, the situation is reversed and

it becomes imperative to correct the chromatic aberration as well, or

ﬁ nd some way of rendering it innocuous. Incidentally, this is a return

to the situation in the early days of electron microscopy, when chro-

matic effects dominated as a result of the relatively poor stabilization

of circuitry at that time.

For quadrupoles, the chromatic aberrations are again different in the

x–z and y–z planes:

∆x

= (C

x′

+ C

)∆

(24)

∆y

= (C

y′

+ C

)∆

in which we have represented the potential and ﬁ eld variation by ∆

[see Eq. (23)].

2.3 Parasitic Aberrations

Parasitic aberrations are, as their name suggests, not intrinsic defects

of electron lenses. They result from imperfections of the construction

or alignment of the lenses or of the entire instrument in question. The

most serious is a (ﬁ rst-order) astigmatism, traditionally associated with

imperfect circularity of the bore of the lens: in fact, Fourier analysis

shows that this astigmatism will usually be the dominant parasitic

effect, whatever the origin of the problem. It is as though a very weak

quadrupole had been superimposed on the lens and the effect can be

cancelled by adding a weak quadrupole with the opposite strength.

Such a device, which in practice has a more complex structure, is

known as a stigmator and several such correctors are routinely incor-

porated in commercial instruments. In high-resolution operation, other

parasitic effects become noticeable and ways of correcting or compen-

sating for these are now known.

A very detailed study of these parasitic aberrations in the context of

electron microscope alignment has been made by Krivanek (Krivanek,

1994; see also Krivanek and Fan, 1992a,b; Krivanek and Leber, 1993,

706 P.W. Hawkes

1994; Krivanek and Stadelmann, 1995). For measurement techniques,

see Saxton (1995a,b, 2000), Saxton et al. (1994), and Chand et al. (1995)

as well as Ishizuka (1994). The work of Zemlin on alignment is also

relevant here (Zemlin et al., 1978; Zemlin, 1979). Among the earlier lit-

erature on parasitic aberrations, we draw attention to the work of

Glaser (1942), Sturrock (1951), Archard (1953), Glaser and Schiske

(1953), Der-Shvarts (1954), and Stoyanov (1955). A long survey has been

written by Yavor (1993) and other references are listed in Hawkes

(1997). The many publications on the stigmator are also relevant; see

Chapter 31 of Hawkes and Kasper (1989) for numerous references to

these.

3 Aberration Correction

3.1 Introduction

The picture of a corrected electron microscope as a standard instru-

ment to which a quadrupole–octopole or sextupole corrector has been

added is an oversimpliﬁ cation. Before correction of the spherical aber-

ration of the transmission electron microscope (TEM) and scanning

transmission electron microscope (STEM) was achieved in the late

1990s, only sporadic attention was paid to any other aberrations that

might become troublesome after C

had been reduced. Now, however,

largely due to the theoretical work of H. Rose and the practical designs

of O. Krivanek and his group, strategies are being developed to correct

all the potentially harmful aberrations in a systematic way. In this

section, we ﬁ rst examine the basic correctors of spherical and chro-

matic aberration and then describe the much more complex correctors

that should be capable of a broader range of correction. The latter are

still at the planning stage or, at best, exist as prototypes.

Spherical aberration is the dominant resolution-limiting aberration

in electron microscopes. It is characterized by the spherical aberration

coefﬁ cient C

, which can be expressed as an integral of the form

CfBzhzdz

∫

[(), ()]

(25)

for magnetic lenses, in which as usual B(z) denotes the magnetic ﬂ ux

on the axis and h(z) is the particular solution of the paraxial ray equa-

tion (1) that vanishes at the object plane. A similar formula, in which

the axial potential distribution φ(z) replaces B(z), gives the spherical

aberration coefﬁ cient of electrostatic lenses. Here we concentrate on

magnetic lenses.

The integrand f[B(z), h(z)] can be written in different ways [see

Hawkes and Kasper, 1989 for many of these and for a general formula

from which all the others can be generated; forms particularly useful

for programming are given by Lencová and Lenc, 1990 (magnetic

lenses) and 1994, 1977 (electrostatic lenses)]. In 1936, Otto Scherzer

derived a nonnegative deﬁ nite form of the integrand, a sum of squared

terms, from which it is clear that the sign of the coefﬁ cient cannot

Chapter 10 Aberration Correction 707

change. Scherzer’s formula was nonrelativistic but Rose (1967/8, see

corrigendum in Preikszas and Rose, 1995) has established a relativistic

version, which essentially conﬁ rms Scherzer’s conclusion. Efforts to

ﬁ nd ﬁ eld or potential distributions for which the integrand vanishes

(Glaser, 1940; Recknagel, 1941) failed, as they were sure to do given the

form of the integrand found by Scherzer. (Attempts to ﬁ nd a loophole

nevertheless continue; see Nomura, 2004 for a recent claim.) Tretner

(1959) later established bounds on the coefﬁ cient.

However, all was not lost for the derivation of Scherzer’s formula

requires a certain number of conditions to be satisﬁ ed: the lens must

possess rotational symmetry, the excitation must be static, only dioptric

operation is permissible (excluding an electron mirror mode), and, in

the case of electrostatic lenses, the potential distribution and its deriva-

tives must be continuous. Object and image must both be real (not

virtual). Scherzer showed (1947) that by relaxing one or the other of

these conditions, a corrector could be devised.

Throughout the second half of the twentieth century, efforts were

made to build and test the various types of corrector. These are

described in detail in Septier (1966), Hawkes (1980), Hawkes and

Kasper (1989, Chapter 41), and Hawkes (1997); some more recent infor-

metry has always seemed a promising approach and as early as the

1950s, Seeliger (1949, 1951) attempted to put Scherzer’s suggestion for

exploiting the idea into practice, as did Möllenstedt (1956). Archard

(1954) showed that relatively simple conﬁ gurations would create the

desired ﬁ eld distribution and Burfoot (1953) found a three-electrode

further experiments were made over the years, including a reassuring

proof-of-principle experiment by Deltrap (1964), but all attempts to

correct a high-resolution microscope objective foundered essentially as

a result of the complexity of the necessary system and of the intrinsic

instability of the technique. A realistic corrector consists of four (or

more) quadrupoles, probably with the “Russian” symmetry, and three

octopoles. The asymmetry between the focusing in the x–z and y–z

planes is not in itself beneﬁ cial, quite the contrary in fact. However, it

creates a situation in which octopoles (which have no paraxial effect,

we recall) can correct the combined spherical and aperture aberrations

of a round lens and the quadrupoles. Even if the quadrupoles and

octopoles are combined into single elements, the task of aligning all

these individual components is clearly formidable. In addition, the

aberrations introduced by the quadrupoles are themselves large, so we

have a situation in which a well-designed round lens with a small

spherical aberration coefﬁ cient is combined with a set of quadrupoles

with large aperture aberrations and octopoles, whose role is to cancel

the overall aperture aberrations of the combination. It is for this reason

that we describe the situation as unstable.

For several decades, quadrupoles and octopoles were the only non-

rotationally symmetric devices envisaged, although it was known that

sextupoles suffer from a spherical aberration that would be suitable, in

principle at least, for use as a corrector (Hawkes, 1965). However, the

geometry that would in principle at least be aberration-free. Numerous

mation is included in Hawkes (2002). Departure from rotational sym-

708 P.W. Hawkes

three-fold symmetry and associated optical properties of such multi-

poles seemed to render them unsuitable for the purpose. But in 1979,

Beck suggested that sextupoles could be combined in such a way that

they would become attractive for correction, and this proposal was

soon thoroughly studied (Crewe, 1980, 1982; Crewe and Kopf, 1980a,b;

Rose, 1981; Ximen, 1983; Ximen and Crewe, 1985). In an interesting

alternative approach, Dragt and Forest (1986) again showed the suit-

ability of sextupoles as correctors.

As we shall see in the following sections, each type of multipole

corrector is now in use. The quadrupole–octopole corrector is used in

the STEM, a probe-forming instrument in which the very considerable

difﬁ culties of correcting a useful area or ﬁ eld of view do not arise. The

sextupole arrangement is incorporated in TEMs. A valuable study of

the performance of these correctors has been made by Haider et al.

(2000).

Of the other ways of achieving correction, Scherzer had high hopes

of the use of high frequency (Scherzer, 1946, 1947), hopes that were

shared by Gabor (1950). The basic idea is easily understood. Electrons

are pictured as reaching the lens from a region close to the optic axis

at the object; those rays that are more steeply inclined will reach the

outer region of the lens (here, an electric lens) slightly later than those

leaving the object at the same time but remaining close to the axis. By

illuminating the specimen with short pulses of electrons and reducing

the excitation of the lens in such a way that the outer electrons encoun-

ter a weaker ﬁ eld, it should be possible to focus them all at the same

place, thus eliminating the effect of spherical aberration, which would

have focused the outer electrons too strongly if the lens strength had

not been weakened. For electrons with energies in the tens of kilovolts

range, the frequency required is found to be of the order of gigahertz

and some experimental studies with a microwave cavity inserted

between the polepieces of a magnetic lens were made by Oldﬁ eld (1973,

1974). These were not pursued, however, and the problems of generat-

ing short enough pulses and, above all, of dealing with the increased

energy spread of the beam were clearly formidable. Recently, Calvo has

reconsidered the technique along very different lines, but his ﬁ ndings

are at present (2005) inconclusive (Calvo, 2002, 2004; Calvo and Lazcano,

2002; Calvo and Laroze, 2002). Yet another way of using dynamic ﬁ elds

for spherical and chromatic aberration correction has been proposed

by Schönhense and Spiecker (2002, 2003), with photoemission and low-

energy electron microscopes in mind. For chromatic aberration, an

ingenious way of inverting the energy distribution of the electron

beam has been found. The electrons are generated at the sample by a

pulsed beam and, after acceleration and collimation, they enter a drift

space, in which the faster electrons draw away from the slower ones,

like horses galloping down the straight in a race. Beyond the drift space

is an accelerator, initially switched off. When the fastest electrons

emerge from it, the electric accelerating ﬁ eld is rapidly switched on and

by suitable choice of the accelerator ﬁ eld, the slower electrons can be

accelerated to a higher energy than the fast electrons, thus effectively

inverting the original energy distribution (Figure 10–4). The chromatic

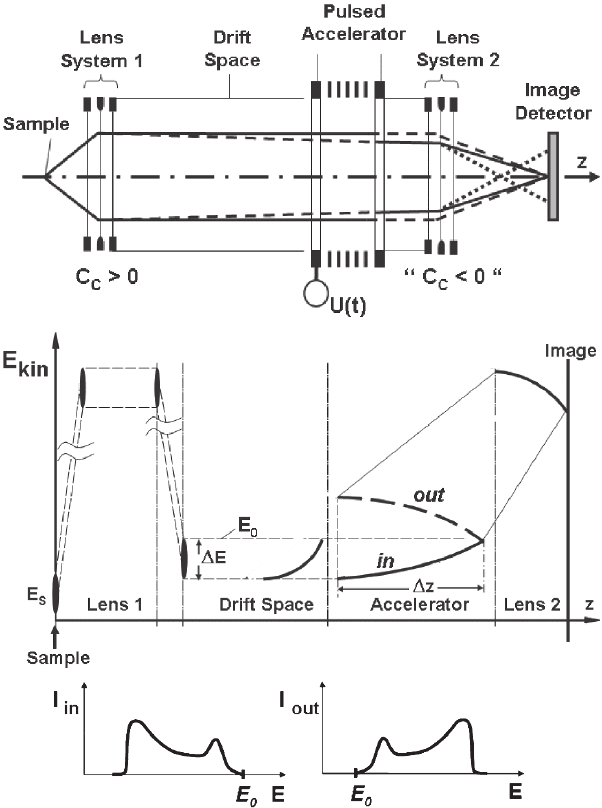
Chapter 10 Aberration Correction 709

aberration of the ﬁ nal lens will then bring the whole beam to a smaller

focus than in the absence of energy inversion. For spherical aberration

correction, Schönhense and Spiecker consider an “electrostatic” lens in

which the lens strength is abruptly altered when the (pulsed) beam

reaches the center. Schönhense and Spiecker explain the correcting

effect by regarding the half-lens as a diverging lens (the converging

Figure 10–4. Chromatic correction based on inversion of the electron energy

distribution. (a) Schematic cross-section of the system (greatly exaggerated in

the radial direction). (b) Electron energy distribution as a function of the

optical path; E

kin

denotes the actual kinetic energy of the electron ensemble.

The distribution E

kin

as a function of z before and after passing the pulsed

accelerating ﬁ eld is denoted by “in” and “out,” respectively. (c) Schematic

representation of the electron energy distribution before and after passing the

accelerator, I

and I

out

. (After Schönhense et al., 2002, courtesy of the authors

and the American Institute of Physics.)

710 P.W. Hawkes

effect of the second half of the lens having been suppressed by switch-

ing off the lens). The image of the object is then virtual and Scherzer’s

result is no longer applicable. Another way of understanding this is to

note that the abrupt change in lens strength is equivalent to a discon-

tinuity in the ﬁ eld and, as for the foil correctors mentioned below, this

is known to offer a way of achieving correction. See also Khursheed

(2002, 2005).

The idea of combining an electron mirror (an electrostatic lens in

which there is a potential barrier too high for the electrons to sur-

mount) with a round lens in such a way that spherical and chromatic

aberrations of the mirror cancel those of the round lens has been

explored and projects based on this are currently being actively

pursued. A major problem is to separate the beam incident on the

mirror from the beam emerging from it and numerous ways of achiev-

ing this have been proposed (see Septier, 1966 and Hawkes, 1980 for

earlier suggestions). We return to this in Section 3.3.4.

Finally, we draw attention to the method in which a ﬁ eld discontinu-

ity is introduced into an electrostatic lens, by covering the bore with

a very thin electron-transparent foil. This was suggested as a means

of achieving chromatic correction by Scherzer in 1948 and has

subsequently been investigated in great detail and with considerable

ingenuity, notably by Typke (1968/9, 1972, 1976) and Scherzer (1980) in

Darmstadt, Hoch et al. (1976) in Tübingen, Munro and Wittels (1977),

and in Japan (Hanai et al., 1986, 1994, 1995, 1998); for recent work, see

Matsuda et al. (2005). The idea has been revived but in a rather

different form by van Aken et al. in Delft (van Aken et al., 2002a,b,

2004, 2005; van Aken, 2005). The use of a cloud of space charge

also falls into this category (see, for example, Haufe, 1958, where

earlier attempts are listed) and has recently been revived by Orloff

(Wang et al., 1995; Tang et al., 1996a,b; Chao et al., 1997) for ion-optical

systems.

Chromatic aberration correction also has a long history, though less

effort has been devoted to it than to spherical aberration correction

because, in the high-resolution imaging mode, developments in micro-

scope design soon rendered the adverse effect of spherical aberration

greater than that of chromatic aberration. This is obvious from an

examination of the phase-contrast transfer function, which is a sinu-

soidal curve in the absence of any energy spread (chromatic effects or

temporal partial coherence) and neglecting the nonvanishing source

size. The sinusoidal curve is damped by an envelope function, repre-

senting the effect of energy spread, but the ﬁ rst zero of the sinusoidal

curve (a measure of the limit of resolution determined by the spherical

aberration) occurs well before the damping curve reduces it to an

unacceptably small value (the so-called information limit). With the

arrival of C

-correctors, however, the situation has changed dramati-

cally and it is now of interest, indeed essential to improve the infor-

mation limit as well by reducing the undesirable effects of energy

spread.

The (axial) chromatic aberration of electron lenses is characterized

by a coefﬁ cient, C

, which can be written as an integral of the form

Chapter 10 Aberration Correction 711

∫

(26a)

for magnetic lenses and

Chdz

′

∫

γφ εφ

()

(26b)

for electrostatic lenses. As in the case of C

(and, indeed, of all the aber-

ration coefﬁ cients), the integrands in Eqs. (26a) and (26b) can be written

in different ways. The ones given here show immediately that C

positive deﬁ nite and the best that can be hoped for in a round lens is

a design for which C

is small.

Over the years, two approaches to the problem of avoiding the limita-

tions imposed by the chromatic aberration of round lenses have

emerged. One is a natural continuation of the efforts to reduce the

energy spread of the beam emitted by the electron gun; by introducing

a monochromator into the column, electrons with energies outside the

chosen range can be eliminated. There is of course some loss of beam

current but since the energy spread of the ﬁ ltered beam can be made

appreciably narrower than that of the original beam, this reduction in

current may be acceptable. This solution is attractive not only in the

imaging mode but also for electron energy-loss spectroscopy (EELS)

and energy-ﬁ ltered transmission electron microscopy (EFTEM). We say

no more about this here; extensive discussion is to be found in the fol-

lowing books, review articles and other publications: Plies (1978), Tang

(1986), Tsuno et al. (1988–9, 1990, 2003, 2005), Tsuno (1991, 1992, 1993,

1999), Reimer (1995), Tsuno and Rouse (1996), Kahl and Rose (1998,

2000), Huber and Plies (1999, 2000), Mook and Kruit (1999a,b, 2000),

Mook et al. (1999, 2000), Oshima (1999), Batson et al. (2000), Kahl and

Voelkl (2001), Martínez and Tsuno (2002, 2004), Benner et al. (2003c),

Mukai et al. (2003a, b), Plies and Bärtle (2003), Ioanoviciu et al. (2004),

Huber et al. (2004), Freitag et al. (2005), and Browning et al. (2006).

The alternative to using a monochromator is to devise a corrector of

chromatic aberration. There are several ways in which such correctors

can be conceived, involving the use of superimposed round lens and

quadrupole ﬁ elds, mixed electrostatic–magnetic quadrupoles, or elec-

tron mirrors.

An early suggestion by S c he rz er (1947 ) i nvolved combining an electro-

static round lens and an electrostatic quadrupole in such a way that the

overall chromatic aberration coefﬁ cient of the combination is negative.

Such a device could then be used to correct the chromatic aberration of a

round lens acting as an objective. This suggestion was taken up by

Archard (1955) and has subsequently been investigated carefully.

In 1961, Kel’man and Yavor showed that the chromatic aberration

coefﬁ cient of a combined electrostatic–magnetic quadrupole can have

either sign, depending on the relative strengths of the component

quadrupoles, and hence that such combined lenses could be used to

correct chromatic aberration. The result was rediscovered by Septier

(1963) and generalized by Hawkes (1964, 1965b). Such combined

hdz

712 P.W. Hawkes

quadrupoles appear in the latest designs of correctors, intended for the

correction of both geometric and chromatic aberrations.

Another possibility, pointed out by Rose (1990), involves the use of

a long Wien ﬁ lter. This too has been studied carefully.

Finally, an electron mirror can be coupled to a round lens in such a

way that the chromatic aberration is cancelled. A practical conﬁ gura-

tion was examined by Rempfer and Mauck (1985, 1986, 1992) and

Skoczylas et al. (1991, 1994). For other proposals, see Shao and Wu (1989,

1990a,b), Rempfer (1990a,b), Crewe et al. (1995a,b, 2000), Tsai (2000),

Crewe (2002), and Bimurzaev (2003, 2004). The simple beam-splitter

employed by Rempfer and Mauck and later by Rempfer et al. (1997) to

separate the incident and emergent beams was dispersive. An improved

version, in which the separator is nondispersive, has been studied by

Preikszas and Rose (1997) and is incorporated in the optical system of

the European SMART (Fink et al., 1997; Wichtendahl et al., 1998; Müller

et al., 1999; Hartel et al., 2000, 2002; Preikszas et al., 2000) and of the

American PEEM3 (Wan et al., 2004; Wu et al., 2004; Feng et al., 2005;

Schmid et al., 2005) projects.

3.2 Spherical Aberration Correctors

3.2.1 Quadrupole–Octopole Correctors

For the correction of spherical aberration, Scherzer proposed a sequence

of cylindrical lenses and octopoles in his seminal paper of 1947 on ways

of avoiding the consequences of his 1936 proof. Cylindrical lenses are

the electron optical counterparts of glass lenses with cylindrical (as

opposed to spherical) faces and are characterized by a round lens and

a quadrupole potential distribution. It was soon realized (Archard,

1954) that quadrupole lenses could be used to advantage instead of

cylindrical lenses and the basic corrector conﬁ guration, which has

remained essentially unaltered, soon emerged (Figure 10–5): a sequence

of three or four quadrupole lenses, with an octopole situated at each

of the line foci to cancel or overcorrect the aperture aberrations in the

x–z and y–z planes, together with a third octopole to complete the task

of correction. (Turnbull, 2004, has recently revived the idea of using

cylindrical lenses in a combined chromatic and spherical aberration

object

plane

quadrupole

round

lens

image

plane

quadrupole 4

final octopole

quadrupole 2

first octopole

quadrupole 3

second octopole

Figure 10–5. The basic quadrupole corrector arrangement, showing four quadrupoles with octopoles

situated at the two line foci and at a third site.

Chapter 10 Aberration Correction 713

corrector.) An important step forward was the introduction of the

Russian quadruplet, which has geometric symmetry and electrical

antisymmetry about its mid-plane, as we have already mentioned. In

common with all multiplets possessing these symmetry properties,

such quadruplets have the same focal length in the x–z and y–z planes.

For a given geometry, the positions of the foci in these planes can then

be made to coincide by suitable choice of the two excitations, where-

upon the quadruplet has the same overall paraxial behavior as a round

lens. Sets of load curves, showing the appropriate excitations as a func-

tion of geometry, are available (see Hawkes, 1970, for many such curves

and Baranova and Yavor, 1989). Another interesting early contribution

was made by Burfoot (1953), who sought the (electrostatic) conﬁ gura-

tion with the smallest number of electrodes that would be free of

spherical aberration. He established suitably shaped apertures in a

three-electrode lens (a remarkable achievement in precomputer times)

but concluded that the necessary tolerances could not be achieved in

practice; a simpler way of attaining the same objective was proposed

by Archard (1958).

In 1964, Deltrap showed that the spherical aberration of a test lens

could be reduced by means of a quadrupole–octopole corrector and

thus conﬁ rmed that the principle of correction was sound. However,

for the next three decades, all attempts to make a corrector capable of

improving the performance of a well-designed objective failed; with

hindsight, we can see that these repeated and disappointing failures

were due to the natural complexity of the system and to the unstable

character of the correction principle mentioned above. Considerable

progress was made, notably in the Darmstadt project (Reichenbach and

Rose, 1968/9; Rose, 1970, 1971a,b; Bastian et al., 1971; Pöhner 1976, 1977;

Bernhard and Koops, 1977; Koops et al., 1977; Koops, 1978, 1978/9;

Koops and Bernhard, 1978, Pejas, 1978; Kuck, 1979; Bernhard, 1980; and

Fey, 1980; see Scherzer, 1978 for a summing up) and in the Chicago

microscope (Crewe et al., 1968; Thomson, 1972; Beck and Crewe, 1974,

1976; Beck, 1977; Crewe, 1978), but neither succeeded in showing any

real gain in electron microscope resolution. The tools necessary for the

adjustment of such devices were not yet available. In the early 1990s,

Zach showed that such correctors could improve the performance of

scanning electron microscopes and this ﬁ nding continues to be

exploited in commercial instruments (Zach, 1989, 2000; Zach and

Haider, 1995a,b; Honda et al., 2004a,b; Kazumori et al., 2004a,b; Uno

et al., 2004a,b). Success came at last in 1997, when Krivanek and col-

leagues, working in the Cavendish Laboratory in Cambridge, built a

corrector equipped with computer control, capable of making the many

necessary adjustments rapidly and systematically. This corrector was

ﬁ tted to a STEM and was hence required to reduce the size of an elec-

tron probe (or to allow the angular aperture and hence the probe

current to be increased). The Krivanek corrector consists of the basic

quadrupoles and octopoles, all under computer control, together with

other multipole ﬁ elds designed to compensate for misalignments

and parasitic aberrations in general. In the second-generation Nion

corrector, 16 quadrupoles are used together with three combined

714 P.W. Hawkes

quadrupole–octopole elements. An additional quadrupole triplet is

situated between the corrector and the probe-forming lens. The correc-

tor itself consists of an alternating sequence of quadrupole quadruplets

and quadrupole–octopole elements (Figure 10–6a). With this arrange-

ment, the center planes of the quadrupole–octopole elements are all

Q Q Q Q Q Q Q Q

Q + O

CCD Det.

Quad. Quadruplet

EELS Aper.

HAADF

1kx1k CCD

MAADF

Diffraction Beam Stop

Gate Valve

Proj. Lens 2

Proj. Lens 1

Pumping Module

OL + Sample Chamber

Sample Exchange

+Storage

Quad. Triplet

C3/C5 Corrector

Cond. Lens 2

Gate Valve VOA

Cond. Lens 1

To CFEG

EELS

Figure 10–6. The Nion quadrupole–octopole corrector incorporated in scan-

ning transmission electron microscopes. (a) The sequence of quadrupole qua-

druplets and quadrupole–octopoles of which the corrector is composed. Q-Q,

quadrupole quadruplet; Q-O, quadrupole-octopole element. (b) Schematic

view of the corrector incorporated in an STEM. (After Krivanek et al., 2004,

courtesy of the authors and the Belgian Microscopy Society.)