Hawkes P.W., Spence J.C.H. (Eds.) Science of Microscopy. V.1 and 2

Подождите немного. Документ загружается.

Chapter 10 Aberration Correction 715

conjugates and are also conjugate to a plane close to the coma-free

plane of the probe-forming lens. In this way, the ﬁ fth-order geometric

aberrations of the combination of corrector and probe-forming lens can

be eliminated. Software will adjust the various components systemati-

cally. The evolution of the corrector, which has been ﬁ tted to many VG

STEMs, to the two SuperSTEMs at Daresbury, and to the Nion STEM,

can be studied in the following publications: Krivanek et al. (1997a,b,

1998, 1999a,b, 2000, 2001, 2002, 2003, 2004), Dellby et al. (2000, 2001),

Batson et al. (2002), Batson (2003), Lupini et al. (2003), Pennycook et al.

(2003), Nellist et al. (2004a,b), Dellby et al. (2005), Bacon et al. (2005),

Krivanek et al. (2005), and Nellist et al. (2006). Figure 10–6b shows

schematically the Nion corrector incorporated in a STEM. The quadru-

pole–octopole corrector designed for an FEI STEM/TEM is described

by Mentink et al. (2004).

3.2.2 Sextupole Correctors

Sextupoles were not among the correctors envisaged by Scherzer in his

1947 paper. In 1965, it was pointed out that the third-order aberrations,

including of course the spherical aberration, of sextupoles have the

same dependence on gradient in the object plane as that of a round lens

(Hawkes, 1965a). However, the fact that the lowest order optical effect

of sextupoles is not linear, as it is in round lenses and quadrupoles, but

quadratic seemed to rule out any hope of using them for aberration

correction. It was not until 1979 that combinations of sextupoles and

round lenses from which the quadratic effects had been eliminated by

compensation were proposed and subsequent developments have con-

ﬁ rmed that such correctors are suitable for incorporation into transmis-

sion electron microscopes. As we have seen, the second-order effect of

a sextupole is characterized by four terms of the form ∫H(z)h

3−n

dz, in

which H(z) represents the ﬁ eld distribution in the (electrostatic or mag-

netic) sextupole and h(z), k(z) are two linearly independent solutions of

the familiar paraxial equation for round lenses (these solutions collapse

to straight lines in the absence of any round lens component). The

integer n takes the four values 0, 1, 2, and 3. All four terms can be made

to vanish by suitable choice of the symmetry of the conﬁ guration; the

simplest is shown in Figure 10–7. Before coupling such a device to a

microscope objective, we must, however, ensure that the coma-free

condition is satisﬁ ed. The (isotropic) coma-free plane of an objective is

situated within the lens ﬁ eld and must hence be imaged onto the front

focal plane of the round-lens doublet in the corrector by means of

another doublet (Figure 10–8). If it should be necessary to eliminate the

anisotropic coma as well as the isotropic coma, an objective design in

which two coils are used in tandem would have to be adopted (Rose,

1971b). Sextupole correction may be traced in the following articles (in

addition to the early publications already cited): Haider et al. (1982, 1995,

1998a–c), Rose (1990b, 2002a,b), Haider and Uhlemann (1997), Haider

(1998, 2000, 2003), Foschepoth and Kohl (1998), Uhlemann et al. (1998),

Urban et al. (1999), Müller et al. (2002), Kabius et al. (2002), Lentzen et

al. (2002), Liu et al. (2002), Benner et al. (2003a,b, 2004a,b), Chang et al.

(2003), Hosokawa and Sawada (2003), Hosokawa et al. (2003), Jia et al.

716 P.W. Hawkes

(2003), Sawada et al. (2004a–c), Haider et al. (2004), Hartel et al. (2004),

Titchmarsh et al. (2004), Hutchison et al. (2005), Haider and Müller

(2005), Müller et al. (2005), and Chang et al. (2006).

3.2.3 Foil Correctors

The suggestion that spherical aberration can be corrected by incorpo-

rating a foil in a rotationally symmetric lens, thus introducing a

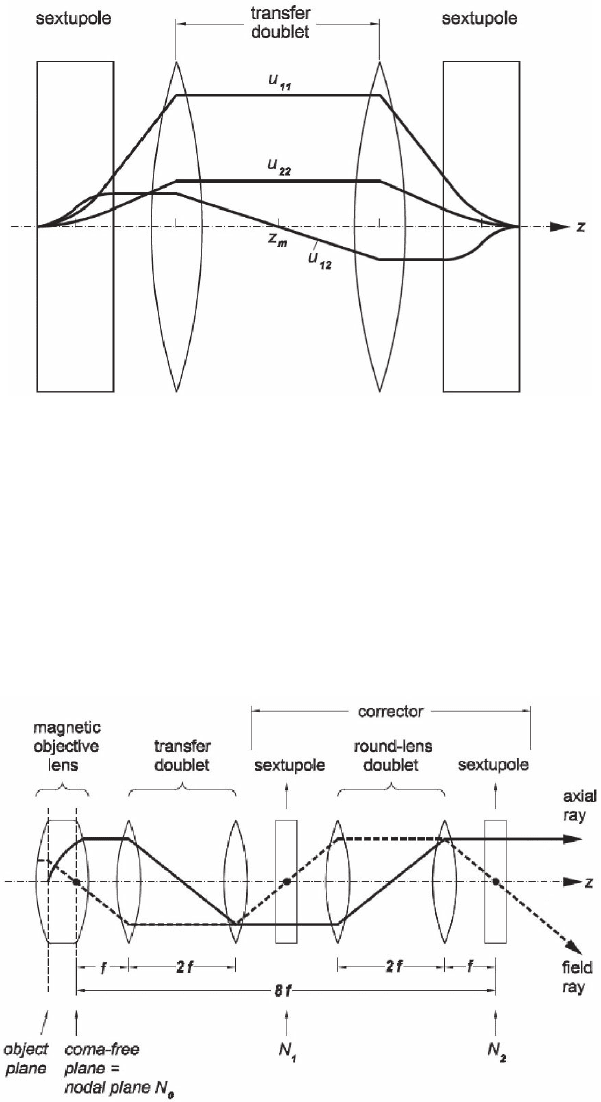
Figure 10–7. Sextupole correctors. Course of the second-order fundamental

rays in the corrector shown in Figure 10–3. (After Rose, 2003c, courtesy of the

author and Springer-Verlag.)

Figure 10–8. Sextupole correctors. Correction of coma as well as spherical

aberration requires a more complex system. The transfer doublet between the

objective lens and the corrector allows for the fact that the coma-free plane

lies within the magnetic ﬁ eld of the objective. (After Rose, 2003c, courtesy of

the author and Springer-Verlag.)

Chapter 10 Aberration Correction 717

discontinuity in the electric ﬁ eld, has been very thoroughly explored

by a Japanese group (see Hanai et al., 1986, 1994, 1995, 1998). In the

earlier studies, the lens shown in Figure 10–9 was ﬁ tted in a TEM and

was shown to reduce the spherical aberration. Subsequent work has

extended this to probe-forming instruments, notably the STEM, where

again the principle was shown to be valid. The lifetime of the foil was,

however, rather short as a result of the build-up of contamination. For

a recent work using a curved mesh, see Matsuda et al. (2005).

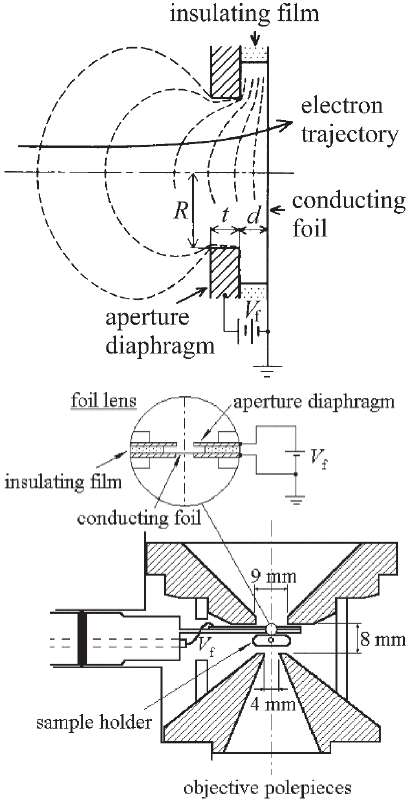
A very different type of foil corrector has been investigated by van

Aken (van Aken et al., 2002a,b, 2004, 2005; van Aken, 2005), who

attempted to exploit the marked increase in the mean free path of

electrons in metal foils at very low voltages. If the latter is atomically

ﬂ at, a mean free path of the order of 5 nm is expected for several metals

Figure 10–9. Foil lens. (a) Schematic cross section of the foil lens. (b) A practi-

cal design, showing the foil lens incorporated in a magnetic objective. (After

Hanai et al., 1998, courtesy of the authors and Oxford University Press.)

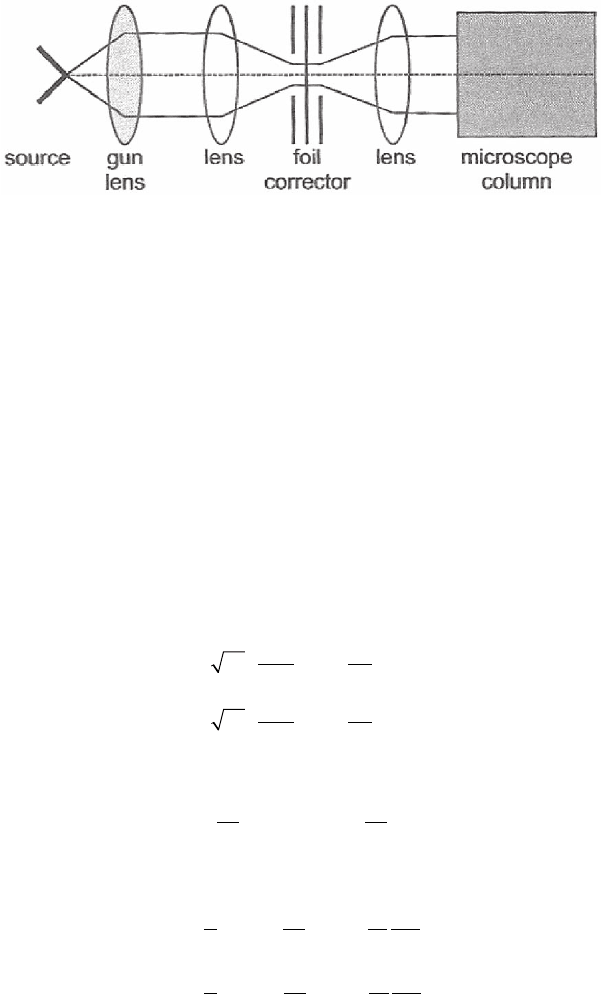
718 P.W. Hawkes

at 5 eV above the Fermi level and a transmission of about 10% is pre-

dicted for thin foils (∼5 nm). By sandwiching the foil between a pair of

electrodes, which ﬁ rst retard the incident electrons and then accelerate

them again, correction of both chromatic and spherical aberration is in

principle possible. Figure 10–10 shows schematically a microscope

column incorporating such a corrector.

3.3 Chromatic Aberration Correctors

3.3.1 All-Electrostatic Correctors

One form of the chromatic aberration coefﬁ cients of a system containing

electrostatic round lens ﬁ elds and electrostatic quadrupole ﬁ elds is

Chhhdz

Chhhd

xxxx

yyyy

′

−

′

−

′

∫

()

()zz

∫

(27)

By introducing the Picht transformation,

HhHh

xxyy

























14//

, (28)

these take the form

CHHHdz

xxx x

′

−

′













−

′











′

−

∫

′′













−

′











∫

φ2

HHdz

(29)

If the quadratic term could be reduced to zero (or at least made smaller

than the absolute value of the negative term), the overall chromatic aber-

ration coefﬁ cient would be negative and the device would hence be suit-

able for use as a corrector. The quadratic term vanishes if the ﬁ eld

distribution is such that the paraxial ray H

(z) = Cφ

1/2

and similarly for

(z), where C is an arbitrary constant. In general, this is not an accept-

able form for H

(z) and H

(z), which must vanish in the object (and

Figure 10–10. The van Aken low-energy foil corrector. Electrons are slowed

down to a very low energy before passing through the correcting foil and then

accelelerated again before entering the microscope column. (After van Aken,

2005, courtesy of the author.)

Chapter 10 Aberration Correction 719

image) planes. If, however, the corrector is telescopic, such a form is

permissible. By substituting this expression for H

(z) and H

(z), and

hence h

(z) and h

(z), back into the paraxial equation, it is trivial to show

that the ﬁ eld functions φ(z) and p

(z) must be related by the formula

′′

−

′

(30)

Conﬁ gurations in which this condition (Scherzer, 1947) is closely

satisﬁ ed have been found by Weißbäcker and Rose (2000, 2001, 2002)

and by Maas and co-workers (Maas et al., 2000, 2001, 2003; Henstra and

Krijn, 2000). In the studies of Weißbäcker and Rose, several conﬁ gura-

tions are examined, in which the complexity increases with the practi-

cal usefulness of the corrector. In the simplest design, four distinct

elements are employed and the corrector is capable of correcting both

the chromatic and the spherical aberration in a scanning instrument.

The ﬁ rst element is a quadrupole, the purpose of which is to render

the incoming beam astigmatic. This is followed by a three-element

corrector consisting of quadrupole ﬁ elds superimposed on a (round)

einzel lens ﬁ eld. A second corrector unit cancels the chromatic aberra-

tion in the other plane. Octopoles are incorporated so that the spherical

aberration can be corrected simultaneously.

Unfortunately, such a corrector introduces large off-axis aberrations

and is hence not suitable for use with transmission (ﬁ xed-beam) elec-

tron microscopes. Weißbäcker and Rose therefore consider ﬁ rst an

extended version in which a third such element is added (Figure 10–11)

and then propose a doubly-symmetric electrostatic corrector (DECO),

in which each correcting element is enclosed within two quadrupole

doublets (Figure 10–12). The symmetry conditions can now be arranged

in such a way that the chromatic aberration and the coma vanish,

while the spherical aberration is corrected by means of octopoles as

usual.

In the complementary investigations of Henstra, Maas, Mentink, and

co-workers, a conﬁ guration consisting of nine elements (Figure 10–13)

is explored. At the outer extremities are quadrupoles to create astig-

matism and subsequently annihilate it. In the center are ﬁ ve combined

round lens and quadrupole units. Two other quadrupoles are included

to match the slowly decaying round lens ﬁ eld of the ﬁ rst and last com-

bined elements. For further work on this approach, see Baranova et al.

(2004).

3.3.2 Mixed Quadrupole Correctors

Quadrupole lenses consisting of four electrodes and four magnetic

poles situated midway between the electrodes have the power of cor-

recting the chromatic aberration of a round lens. They must of course

be part of a suitable conﬁ guration and are currently incorporated in

the complex superaplanator and ultracorrector described in Section 3.4.

Such correctors have not been seriously considered for correction of C

in the transmission electron microscope in recent years, for the simpler

conﬁ gurations increased the spherical (and other) aberrations unrea-

sonably. However, they have been reconsidered recently (Haider and

720 P.W. Hawkes

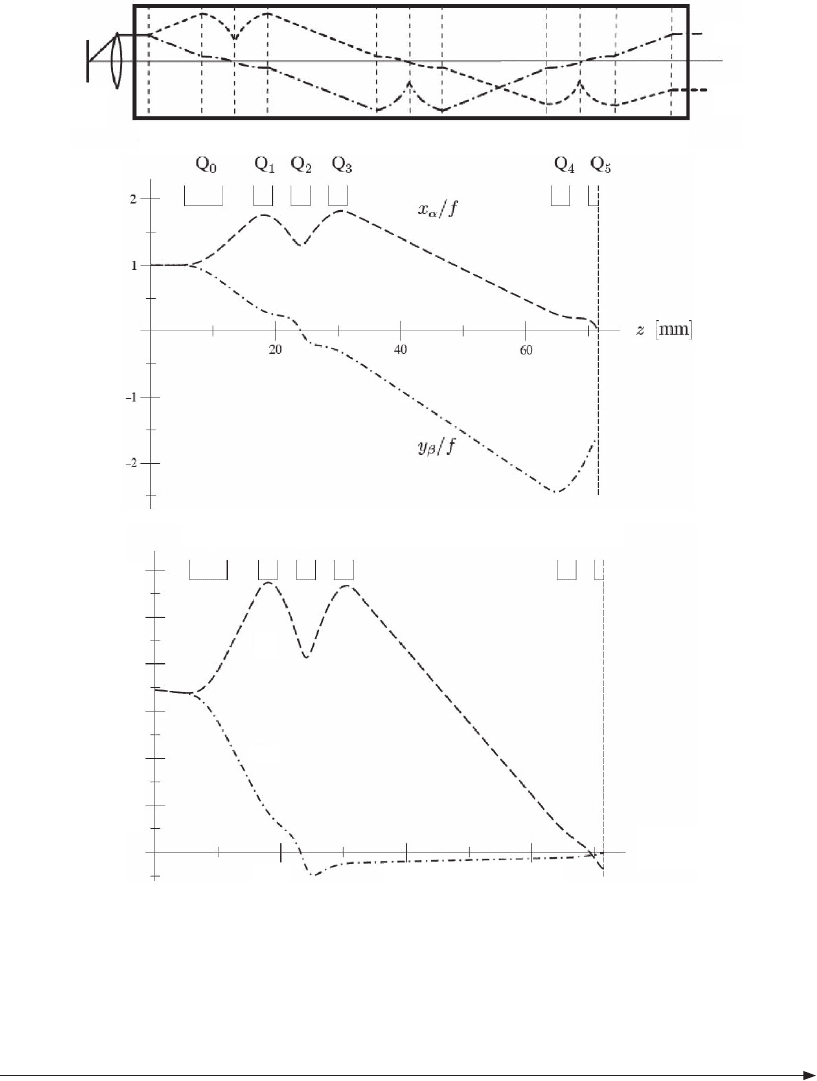
Figure 10–11. Aplanatic corrector of spherical and chromatic aberration. (a) A three-element corrector,

in which the ﬁ rst and third elements cancel the chromatic aberration in the x–z plane while the central

element cancels it in the y–z plane. (b) Axial rays in the ﬁ rst half of the corrector. (c) Field rays in the

ﬁ rst half of the corrector. (After Weißbäcker and Rose, 2002, courtesy of the authors and Oxford Uni-

versity Press.)

20 40 60

z [mm]

Figure 10–12. Doubly symmetric electrostatic corrector (DECO) of spherical and chromatic aberra-

tion. (a) Axial and ﬁ eld rays in one-half of the DECO; each half consists of a corrector enclosed between

quadupole doublets. (b) Details of the axial rays in one unit of the DECO. (c) Details of the ﬁ eld rays

in the ﬁ rst half of the DECO. (After Weißbäcker and Rose, 2002, courtesy of the authors and Oxford

University Press.)

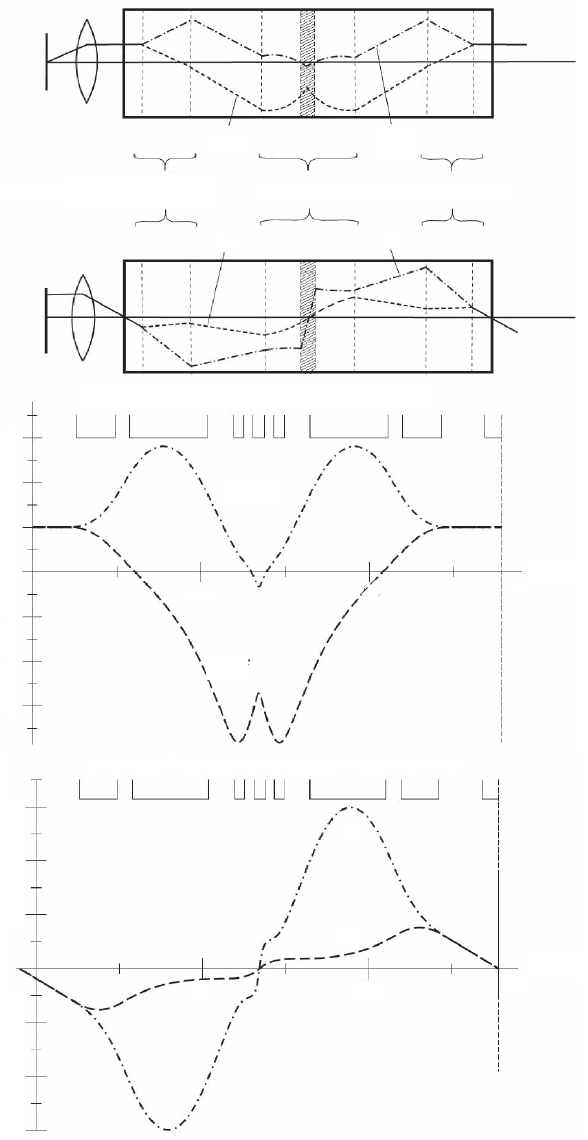
Chapter 10 Aberration Correction 721

entrance

objective-

lens

object

doublet

correcting element

exit doublet

/ f

z [mm]

–1

–2

–3

100

z [mm]

–2

–4

–6

100

aii)

ai)

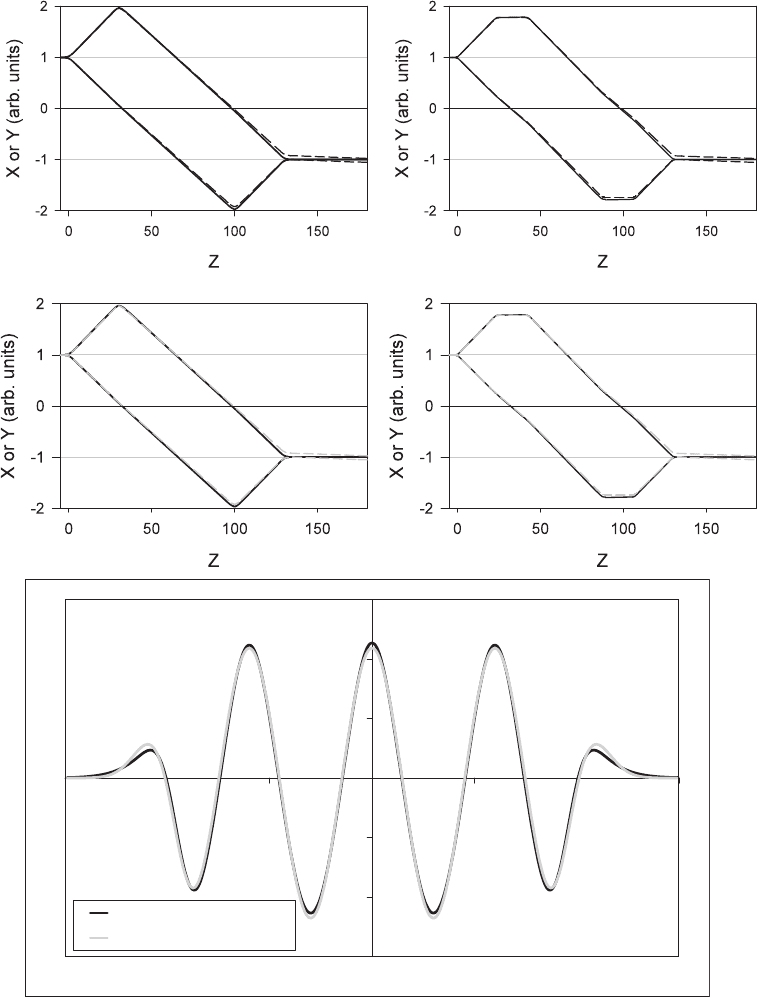
722 P.W. Hawkes

Figure 10–13. Electrostatic correction of chromatic aberration. (a) Rays in a quadrupole quadruplet

or sextuplet. (b) Match between the potentials needed to satisfy Scherzer’s condition and those in the

corrector. (See color plate.)

-3E+08

-2E+08

-1E+08

0E+00

1E+08

2E+08

3E+08

-15 -10 -5 0 5 10 15

Z [mm]

Quadrupole field [V/m/m]

Scherzer's condition

3D Quadrupole

Chapter 10 Aberration Correction 723

Müller, 2004), for there exist more elaborate arrangements that do not

have this handicap. Details are not available as yet.

3.3.3 Wien Filters and Correction

In an attempt to design a corrector that is reasonably easy to align and

consists of as few separate elements as possible, Rose (1990) has exam-

ined the properties of an inhomogeneous Wien ﬁ lter. If such a ﬁ lter is

to correct chromatic aberration instead of acting as a highly dispersive

device, it must be nondispersive, double focusing, and free of all second

rank aberrations (apart from the desired rotationally symmetric chro-

matic aberration). We have seen in other electron optical conﬁ gurations

how useful symmetry and antisymmetry are to eliminate certain aber-

rations. Here, all geometric second-order aberrations can be excluded

by ensuring that the fundamental rays are antisymmetric with respect

to the mid-plane of the ﬁ lter or to the mid-plane of the ﬁ rst or second

half of the ﬁ lter. Rose’s extremely complete study shows that a conﬁ gu-

ration can be found that will correct chromatic aberration. Further-

more, by adding sextupoles before and after the corrector (Figure

10–14), axial chromatic aberration and spherical aberration can be cor-

rected independently.

This idea has been revived by Mentink et al. (1999) and Steffen et al.

(2000), who were seeking further simpliﬁ cation and reduction of the

number of optical elements and excitations. Rose’s device consisted of

a relatively long combined multipole (octopole or dodecapole) with

both magnetic and electrostatic components (as in all Wien ﬁ lters) for

chromatic correction, with external sextupoles. In this new design,

chromatic correction is achieved by means of the usual magnetic and

electrostatic ﬁ elds of the Wien ﬁ lter onto which an electrostatic quad-

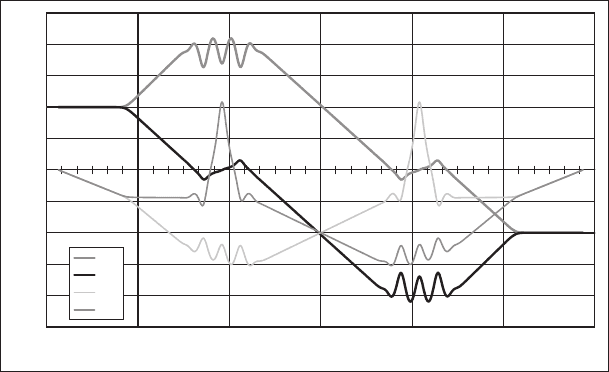
Figure 10–13. Continued (c) Gaussian rays in the sextuplet after correcting elements have been placed

at the line foci. The chromatic aberration has been corrected and the residual chromatic aberration of

magniﬁ cation is small. (After Maas et al., 2001, 2003, courtesy of the authors, SPIE, and the Microscopy

Society of America.)

-2.5

-2

-1.5

-1

-0.5

0.5

1.5

2.5

-90 -60 -30 0 30 60 90

Z [mm]

X or Y (arb. units)

724 P.W. Hawkes

rupole is superimposed. No other magnetic ﬁ elds are required. Spheri-

cal aberration is corrected by superimposing sextupole ﬁ elds, which

are of opposite sign in the ﬁ rst and second halves of the Wien ﬁ lter

zone. Unwanted aberrations are introduced by the fringing ﬁ elds at the

extremities of the corrector but it should be possible to control them by

shaping the ends of the electrodes and magnetic poles.

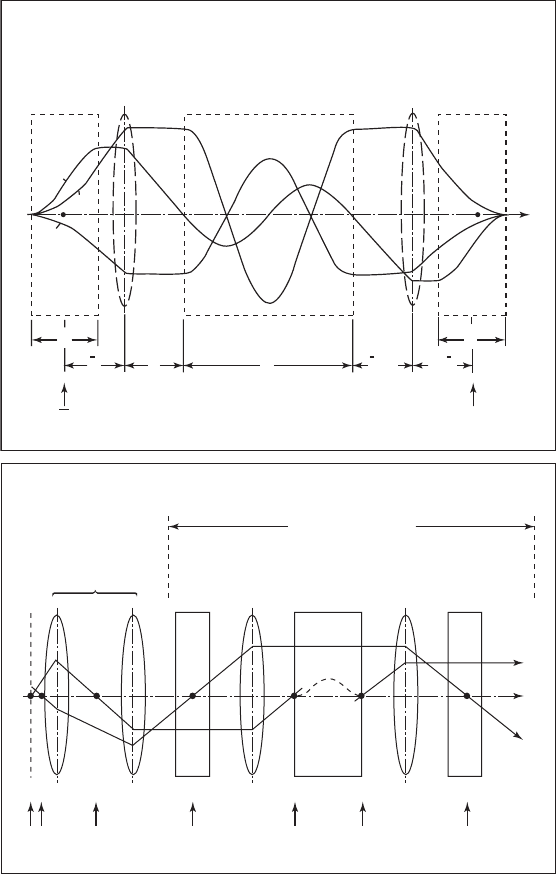
Figure 10–14. (a) Wien ﬁ lter ﬂ anked by two sextupoles and the necessary

transfer lenses, capable of correcting both chromatic and spherical aberration.

The nodal points N and N

–

coincide with the coma-free points. (b) The corrector

in conjunction with a coma-free objective. (After Rose, 1990, courtesy of the

author and the Wissenschaftliche Verlagsgesellschaft.)

sextupole 1

transfer

lens 1

achromator

transfer

lens 2

sextupole 2

βδ

–U

δδ

ββ

OA O

corrector

object

plane

objective

double lens

sextu-

pole 1

transfer

lens 1

achro-

mator

transfer

lens 2

sextu-

pole 2

axial

ray

field

ray