Hawkes P.W., Spence J.C.H. (Eds.) Science of Microscopy. V.1 and 2

Подождите немного. Документ загружается.

605

LEEM and SPLEEM

Ernst Bauer

Low-energy electron microscopy (LEEM: http://www.leem-user.com)

is an imaging method that makes use of elastically backscattered elec-

trons with energies below about 100 eV, frequently with less than 10 eV.

In contrast to transmission electron microscopy (TEM), which gener-

ally works with electrons in the 100 keV range where backscattering is

negligible, the backscattering cross sections for low-energy electrons

are large enough to make them useful for surface imaging. This was

already evident in the classical diffraction experiments of Davission

and Germer,

but it took 35 years before the use of slow diffracted

electrons for surface imaging was suggested

and another 23 years

before convincing images could be published.

Thus, although diffrac-

tion of slow electrons and imaging with slow emitted electrons with

resolution in the micrometer range were demonstrated

before TEM

reached submicron resolution,

LEEM became a viable imaging method

only much later.

The reasons for this late appearance of LEEM in electron microscopy

are 2-fold: (1) for LEEM well-deﬁ ned surfaces are necessary, which in

general requires ultrahigh vacuum (UHV) and efﬁ cient surface clean-

ing procedures. Although these have been available for some time in

glass systems such as in Farnsworth’s low-energy electron diffraction

(LEED) systems,

6–8

glass systems are not very user friendly and metal

UHV technology did not come into widespread use until the beginning

of the 1960s. In fact, the ﬁ rst display type LEED system that started the

revival of LEED was a glass system

9,10

as was the ﬁ rst unsuccessful

model of an LEEM system.

(2) There was the widespread belief in the

electron microscope community based on the fundamental theoretical

work of Recknagel on emission electron microscopy

that the chro-

matic aberration of the objective lens would limit the resolution to such

an extent that LEEM would be unattractive. This of course was a mis-

understanding as already pointed out in the early phase of the develop-

ment of LEEM.

12,13

In the decades since then LEEM has developed slowly

into a powerful surface imaging technique as recounted elsewhere.

1 Introduction

606 E. Bauer

In the past 10 years developments concentrated on the combination

of LEEM with X-ray induced photoemission electron microscopy

(XPEEM), which resulted in the spectroscopic photoemission and

low-energy electron microscope (SPELEEM),

15,16

and on the correction

of the aberrations of the objective lens.

Despite these efforts LEEM is

still far behind the technological state that TEM has now reached.

This chapter reviews the basics of LEEM, its present state of art, and

its applications. An associated imaging method, spin-polarized LEEM

(SPLEEM), which gives magnetic information, will also be discussed.

Other methods, such as mirror electron microscopy (MEM), which

gives information mainly on the local surface potential, Auger electron

emission microscopy (AEEM), which gives chemical information,

electron energy loss microscopy (EELM), which gives some electronic

information, and secondary electron emission microscopy (SEEM),

will be mentioned only brieﬂ y because they have been used much less

frequently, although they are also useful. Photoelectron emission

microscopy (PEEM), in particular XPEEM, is included only in connec-

tion with the discussion of SPELEEM because it is the subject of another

chapter.

To understand the possibilities and limitations of LEEM and of the

associated techniques, a fundamental understanding of the interac-

tions of slow electrons with condensed matter is necessary. The follow-

ing interactions have to be taken into account: elastic scattering, inelastic

scattering, and quasielastic scattering (phonon and in magnetic materi-

als magnon scattering). The interactions of slow electrons with matter

are vastly different from those of fast electrons. In ferromagnetic

materials they depend in addition upon the relative orientation of the

spin of the incident electrons and the electrons in the matter.

Consider ﬁ rst elastic scattering. Because of its low velocity

vEm= 2/

the interaction time of a slow electron is much longer than of the fast

electrons used in TEM and an n-electron atom may no longer be con-

sidered as undisturbed but becomes an n + 1 electron system during the

interaction. Therefore the incident electron experiences the temporary

excitations of the n-electron atom. This can be taken into account by

adding a correlation potential to the potential of the ground state n-

electron atom. Similarly the repulsive interactions between electrons

with the same spin due to the Pauli principle cause a spin-dependent

potential that also has be added. As a consequence, the scattering of slow

electrons by the atoms that constitute the condensed matter can no

longer be described by the ﬁ rst Born approximation, which assumes a

static atom in the ground state and which is a good approximation at

high energies. Instead, a partial wave analysis is necessary, taking into

account the exchange and correlation potentials.

18,19

No calculations of

this type for condensed atoms, whose potentials are truncated by overlap

with the neighbor atoms, are available. Fortunately the magnitudes of

the correlation and exchange potential decrease rapidly with energy so

2 Electron Beam–Specimen Interactions

Chapter 8 LEEM and SPLEEM 607

that they may be neglected in the energy range of conventional LEED

studies (usually above 30 eV). In LEEM, however, they should be taken

into account. This is a formidable task that has not been mastered up to

now. Therefore, only some results of partial wave analysis calculations

for truncated ground state potentials will be given here.

In the partial wave analysis

the incident plane wave and the outgo-

ing scattered wave are expanded into spherical harmonics centered

at the atom, and the phase differences η

between the incident and

outgoing partial waves are calculated. In the nonrelativistic case the

scattering amplitude is given by

f(θ, k) = (1/2ik)Σ(2l + 1)[exp(2iη

− 1)]P

(cos θ) (1)

with the sum over l extending from zero to inﬁ nity. k is the wave

number and the P

’s are Legendre polynomials. The intensity distribu-

tion of the scattered electrons as a function of scattering angle θ and

energy

Ek∼

is then simply ∼|f(θ, k)|

. Figure 8–1 shows the angular

distribution of the scattered intensity of 50 eV electrons, calculated in

this manner for realistic solid state Ag, Al, and Cu atomic potentials.

It shows that not only is the total scattering cross section of Cu (Z = 29)

smaller than that of Al (Z = 13), but also its back-scattering cross section,

and that Al scatters nearly as much as the much heavier Ag atom

(Z = 47). The scattering is, however, strongly energy dependent. This is

illustrated for the scattering into a 30° cone around the backward direc-

tion in Figure 8–2,

which shows that at very low energies Cu scatters

nearly as strongly as W (Z = 74) while Al and Ag scatter much more

weakly in the backward direction. It should be noted that the zero of

the energy is the inner potential resulting from the overlap of the free

atom potentials so that the maxima of the W and Cu backscattering

cross sections are just around the vacuum level.

Figure 8–1. Angular distribution of 50 eV electrons elastically scattered from

Ag, Al, and Cu atoms in the solid state.

0° 50°

150°

100°

I (u) (a

)

608 E. Bauer

In condensed matter the electrons are, of course, not only scattered

within one atom but also by the atoms surrounding it, causing strong

multiple scattering. This is taken into account in LEED in the dynamic

theory of electron diffraction.

21,22

Another way to look at the problem

of scattering in a periodic system is in terms of the band structure

theory if we assume that the n + 1-electrons system (n crystal electrons

+ incident electron) does not differ signiﬁ cantly from the n-electron

system (Koopman’ theorem

). Then the 180° backscattering from a

single crystal surface is determined by the band structure E(k) perpen-

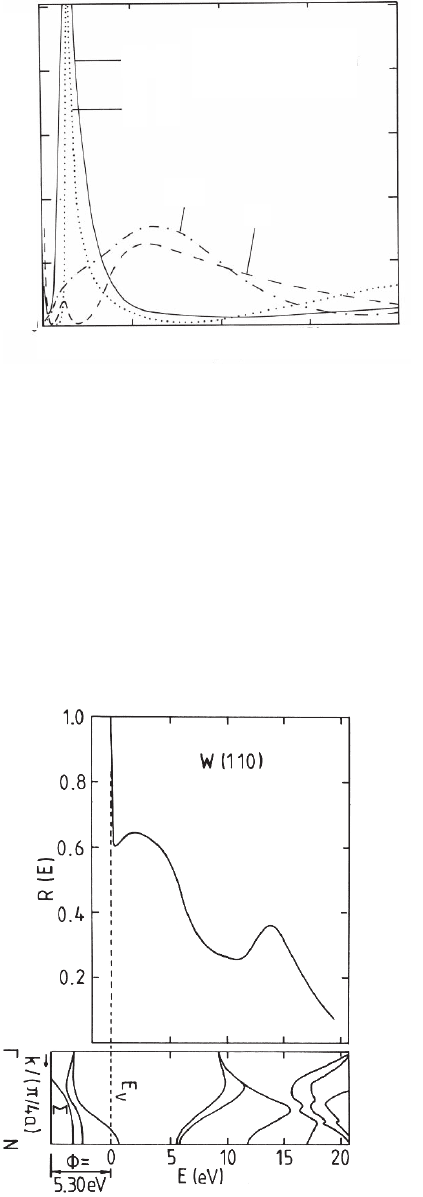
dicular to the surface. This is illustrated in Figure 8–3 for the W(110)

surface.

The band structure in the [110] (ΓN) direction has a wide

Backscattering into

angular region from

150° to 180°

050100 150 200

E (eV)

QR (Å

)

Figure 8–2. Energy

dependence of the

backscattering into a

30° cone around the

backward direction for

Ag, Al, Cu, and W

atoms in the solid

state.

Figure 8–3. Normal incidence

specular reﬂ ectivity of a W(110)

surface (top) and band struc-

ture along the surface normal

(bottom).

Chapter 8 LEEM and SPLEEM 609

band gap between about 1 and 6 eV above the vacuum level. An elec-

tron incident in this direction, therefore, does not ﬁ nd allowed states

in the crystal and forms an evanescent wave. The extinction length of

this electron wave in the crystal is quite short in the center of the gap,

only about two monolayers,

so that the electron is reﬂ ected before it

is attenuated signiﬁ cantly by inelastic scattering. This, together with

the strong backscattering cross section, causes the high reﬂ ectivity at

about 2–3 eV. The second reﬂ ectivity peak is due to the low density of

states in the crystal as indicated by the steep bands. The band structure

inﬂ uence is strongly orientation dependent. For example, on the W(100)

surface the band gap is located between 3 and 5 eV above the vacuum

level,

24,26

which causes a pronounced reﬂ ectivity peak at about 4 eV.

This is preceded by a deep reﬂ ectivity minimum, which is caused by

the strong inelastic scattering of the electron that could otherwise

penetrate deeply into the crystal. A second reﬂ ectivity peak occurs

around 8 eV where the density of state in the crystal is small. This

simple picture neglects the inﬂ uence of surface effects. For quantitative

agreement between experiment and theory the surface barrier,

surface

resonances,

and reconstruction have to be taken into account. For

LEEM these details are not important, at least at the present state of

art, because they determine mainly the reﬂ ected intensity and have

little inﬂ uence on the contrast.

The main factor that determines the high surface sensitivity of LEEM

is in general not the inﬂ uence of the band structure and of elastic scat-

tering but the strong attenuation of slow electrons by inelastic scatter-

ing. Inelastic scattering is due to single electron excitations (electron

hole pair creation) and collective electron excitations (plasmon cre-

ation). In the energy range of LEEM single electron excitations mainly

involve valence band and weakly bound outer shell core electrons. The

universal inelastic mean free path (IMFP) curves usually found in the

literature are of rather limited value at the low energies used because

they do not take into account the differences in the electronic structure

of the various materials. Therefore, only some general features will be

discussed and some speciﬁ c examples will be given. In materials that

may be described approximately by a free electron gas imbedded in a

homogeneous background of equal charge (“jellium model”) the IMFP

is a function of k/k

Fermi wave number) with the electron density

as parameter.

18,19,28

As an example, the attenuation length µ = (IMFP)

−1

of Al, for which the free electron approximation is good, is shown in

Figure 8–4 together with the attenuation coefﬁ cient ν due to elastic

backscattering, assuming a random distribution of Al atoms with bulk

density (“randium model”).

29,30

The initial rise of µ until the volume

plasmon creation threshold at E

= 17.5 eV (above vacuum level) is due

to single electron excitations. The maximum of µ and the corresponding

minimum of about 0.3 nm of the IMPF at about 37 eV is mainly due to

plasmon losses. Figure 8–4 also shows that attenuation by elastic back-

scattering is much weaker above E

than that by inelastic scattering.

For most metals the jellium approximation is not useful, in particu-

lar for transition and noble metals. For example, in contrast to jellium,

transition metals have a high density of unoccupied states just above

610 E. Bauer

the Fermi level into which excitations can occur. The deviation from

jellium can be partially taken into account by replacing the ω depen-

dence in the Lindhard dielectric function ε

(ω, q), which is used in the

jellium calculations, by that obtained in the experiment for zero

momentum q transfer, that is by optical data for which q = 0. Results

of such calculations

give typically minimum IMFPs in metals of

0.3–0.5 nm at energies between 30 and 120 eV for Mg and Au, respec-

tively, with a rapid increase at low energies to values as high as 2.4 nm

in Si and 3.5 nm in W at 10 eV, for example. Figure 8–5 illustrates the

agreement between theory and experiment that can be obtained in

this approximation.

The deviations below E − E

= 5 eV are irrelevant

for LEEM because the work function of Au is about 5 eV; those above

50 eV are probably due to inaccurate 5p and 4f ionization cross

0.1

0.2

0.3

50 100 150 200

Vac

(eV)

µ,ν (Å

–1

)

Figure 8–4. Energy dependence of the attenuation coefﬁ cients µ,ν of slow elec-

trons in Al by inelastic scattering and elastic backscattering, respectively.

–1

E–E

(eV)

(nm)

Figure 8–5. Energy dependence of the inelastic mean free path of electrons

in Au. The points and dots are experimental data and the dashed and solid

lines are theoretical data using different approximations.

Chapter 8 LEEM and SPLEEM 611

sections. The agreement is surprisingly good considering that the q

dependence of ε has been approximated by simple expressions and

that correlation and exchange have not been taken into account. At

energies below several 10 eV these are of comparable importance for

inelastic scattering as for elastic scattering, in particular the inﬂ uence

of the detailed band structure and of nondirect (q # 0) transitions.

For example, inclusion of exchange in the dielectric model of the IMFP

gives IMFP values that are by a factor of 1.3 and more larger than

without exchange.

The IMFPs calculated in this approximation for insulators are even

larger, such as 6 nm at 10 eV for KCl.

For several groups of insulators

with large band gaps (condensed noble gases, N

, and organic dielec-

trics such as benzene or methane) no electronic excitations are possible

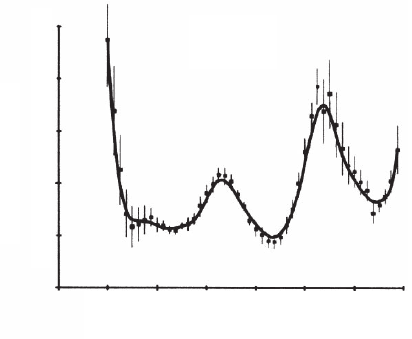
at low energies. Here the (quasi)elastic mean free path (EMFP) deter-

mines the sampling depth. EMFP measurements in the energy range

from 2 to 15 eV give EMFPs up to 10 nm.

An example is shown for

solid Xe in Figure 8–6.

Thus the MFP may be very long at low ener-

gies (≤10 eV) while at energies between about 30 eV and 100 eV, depend-

ing upon the material, it may be only a few tenths of a nm. The large

mean free paths (MFPs) at very low energies are, however, not general.

They depend strongly on the density of unoccupied states into which

bound electrons can be excited as clearly evident in an insulator with

wide band gaps.

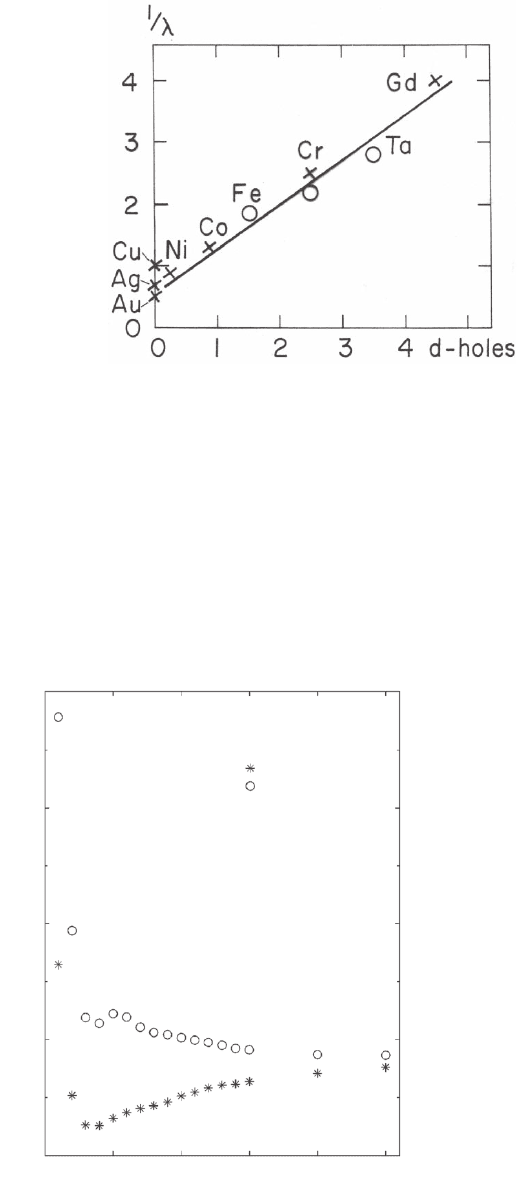
These are extreme cases inasmuch as their band

gaps are so large that the density of unoccupied states becomes

signiﬁ cant only at several electronvolts above the vacuum level. At the

other extreme are transition metals with their unﬁ lled d bands with

high density of states just above the Fermi level. Here the IMFPs are

very short as seen in Figure 8–7

in which the reciprocal values of the

IMFPs are plotted as a function of the number of d holes. The values

shown are for electrons with energies between 5 and 10 eV above the

Fermi energy. For Fe the IMFP is only about 0.5 nm and for Gd only

Solid Xe

T = 45 K

345678

Electron Energy (eV)

Mean Free Path (nm)

Figure 8–6. Energy dependence of the elastic mean free path of slow electrons

in solid Xe.

612 E. Bauer

0.25 nm. In ferromagnetic materials the density of unoccupied states

differs between majority and minority spin states, which causes

corresponding differences in the excitation probabilities. Calculations

that take this into account show a signiﬁ cant difference between the

IMFPs of incident electrons with majority and minority spin as seen

in Figure 8–8.

The zero of the energy is the Fermi energy; the work

Figure 8–7. Reciprocal inelastic mean free path in nm

−1

of electrons with ener-

gies between 5 and 10 eV above the Fermi level as function of the number of

holes in the 3d and 4d shell.

spin down

0.0 5.0 10.0 15.0 20.0 25.0

Electron Energy (eV)

IMFP(Å)

spin up

Figure 8–8. Energy

dependence of the inelas-

tic mean free path of

majority and minority

spin electrons in Fe.

Chapter 8 LEEM and SPLEEM 613

function of Fe is 4.5 eV so that 1 eV above the vacuum level the IMFPs

are only 0.6 and 0.2 nm for majority and minority spin electrons,

respectively. At 10 eV above the vacuum level the corresponding values

are 0.45 and 0.3 nm, which are much lower than the 1.6 nm obtained

from the dielectric theory discussed above. For more information see

Bauer.

While the knowledge of reliable absolute numbers for elastic and

inelastic mean free paths at low energy is still limited, the inﬂ uence

of phonon and magnon excitation on the effective sampling depth is

much less understood. Both processes involve only small energy

losses up to several 100 meV but can occur with large momentum

transfer. In LEEM only the electrons in a diffraction spot and its

immediate environment contribute to the image formation. Therefore

energy losses with momentum transfer larger than that determined

by the radius of the contrast aperture cause an attenuation of the

intensity contributing to the image formation. At not too high tem-

peratures this can be taken into account by the Debye–Waller factor.

At higher temperatures multiphonon and -magnon excitations occur

that cause an increased attenuation, which may be described by an

anharmonic Debye–Waller factor.

In this conventional description of

the inﬂ uence of phonons on the scattering from surfaces there is no

thickness dependence. However, in thin ﬁ lms the number of electrons

scattered outside the contrast aperture increases with increasing

thickness so that an effective attenuation coefﬁ cient could be deﬁ ned.

This has not been done to date for several reasons: (1) there are no

numbers for the cross sections for phonon and magnon scattering that

could be compared with those for inelastic scattering, (2) with increas-

ing temperature there is frequently atomic disordering that causes

diffuse scattering, and (3) at high temperatures thin ﬁ lms usually

break up into three-dimensional crystals before attenuation by these

processes becomes signiﬁ cant. A rough idea of the inﬂ uence of thermal

vibrations on the attenuation length may be obtained from the analy-

sis of LEED patterns from Cu single crystal surfaces. At 50 eV the total

attenuation length, which includes elastic backscattering, inelastic

scattering, and phonon scattering, from the (111) surface is 0.33 nm at

300 K versus 0.34 nm at 0 K.

The difference is well within the limits

of error of the values so that at least at this energy phonon scattering

does not limit the sampling depth.

According to the present state of understanding the sampling depth

of LEEM and SPLEEM is primarily determined by inelastic and elastic

backscattering. Depending upon the energy and electronic structure

of the material, the sampling depth may be as small as a few tenths of

a nanometer, for example, around the plasmon excitation maximum,

in transition metals with a high density of unoccupied states above the

Fermi level, or in band gaps along the k direction normal to the surface.

On the other hand, sampling depths as large as several nanometers

can occur at very low energies, for example, in insulators and free

electron like metals. In many cases this allows tuning of the sampling

depth by proper choice of the energy, which makes LEEM and SPLEEM

ideal for imaging of surfaces and thin ﬁ lms.

614 E. Bauer

The electron optics of an LEEM/SPLEEM instrument in the imaging

section is essentially the same as in emission electron microscopes,

which date back to the 1930s. In these microscopes the specimen is the

cathode of a so-called cathode lens in which the slow emitted electrons

are accelerated in a high ﬁ eld to the ﬁ rst of several image-forming elec-

trodes of an electrostatic lens or to the entrance of a magnetic lens. This

lens is the objective lens of the microscope, which produces a primary

image with fast electrons. The subsequent electron optics is basically

the same as in TEM. In fact, the ﬁ rst objective lens used in LEEM was a

modiﬁ ed version of an electrostatic triode lens developed for PEEM.

To do LEEM with such a system fast electrons have to be injected from

the high-energy side of the objective lens along its optical axis. In the

cathode lens they are decelerated to the desired low energy at the speci-

men. To be able to produce an image, this incident beam has to be sepa-

rated from the reﬂ ected beam by a beam divider. As a consequence an

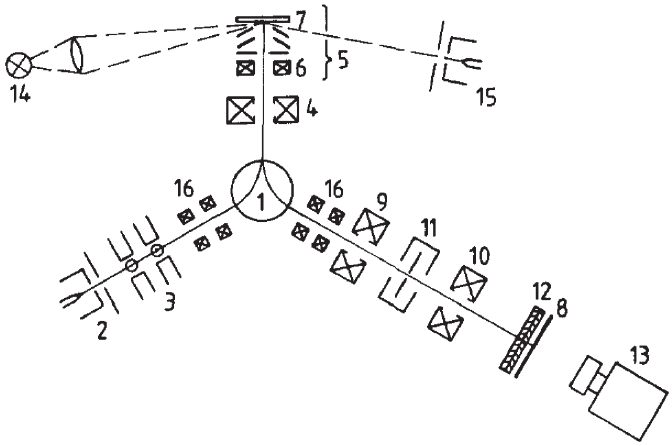
LEEM or SPLEEM system has a bent optical axis. A schematic of the ﬁ rst

instrument is shown in Figure 8–9.

The beam separator (1) deﬂ ects the

incident beam from a ﬁ eld emission gun (2) that is focused by two

quadrupoles (3), the deﬂ ection ﬁ eld (1), and optionally by a collimator

lens (4) into the back focal plane of the objective lens (5). They reach the

specimen (7) on parallel trajectories with an energy that is determined

by the adjustable potential difference between ﬁ eld emitter and speci-

men. The specimen is imaged by the elastically reﬂ ected electrons into

the center of the beam separator, its diffraction pattern into the back

focal plane of the objective lens where the angle-limiting contrast aper-

ture is located. The astigmatism of the objective lens is corrected with

Figure 8–9. Schematic of the ﬁ rst LEEM instrument. For explanation see text.

3 Instrumentation